一种能实现免脱帽人脸识别系统算法
张彦虎,鄢丽娟,张彦军
(1.广东松山职业技术学院 计算机与信息工程学院,广东 韶关 512126; 2.国父大学,菲律宾 曼达路尤 1550; 3.中山大学 数据科学与计算机学院,广州 510006; 4.甘肃五环公路工程有限公司,兰州 730000)
0 引言
近年来,随着计算机人脸识别技术的发展,人脸识别已逐步应用于各行各业的人员身份识别领域[1],其中部分特殊行业员工在使用人脸识别系统进行身份识别时具有一定的特殊性,比如舰艇员工、矿工等,在该应用场景下,待识别人员大多带有不同类型容易遮挡脸部的穿戴设备,如帽子、头盔等,传统人脸识别技术为了达到一定准确率,多要求被识别者去除遮挡物,否则容易造成识别失败等问题,但是,强制性要求被识别者去除遮挡物可能会产生如下不良影响:1)部分请况下此举不人性化;2)容易导致系统效率低;3)可能会产生安全隐患等一系列问题。
目前人脸识别流行的技术方案两个方向[1],其一是基于脸部全局特征进行识别,该方案可以很好地体现人脸特征的整体情况,其中较为经典的方法有PCA[2]、LDA[3]等方法;其二是基于脸部局部特征进行识别,该方案主要侧重于体现脸部的细节,其中较为典型的方法有LBP[4]、SIFT[5]、HOG[6]等方法。
对于基于脸部局部特征进行识别的方法,研究人员进行了多角度的探索,文献[7-8]基于HOG算法做了改进,改进HOG算法在图像处于不同光照、旋转等情况下的识别率有所提高;文献[9]采用LBP分块方法进行图像识别,取得不错的效果;文献[10-12]基于LBP算法进行了适当改进,在识别率上有所提升;文献[13]提出CLBP算法,其主要改进点是在LBP基础上融合了局部差异值和中心像素灰度值分析等技术;文献[14]利用模块方差的大小选择不同的阈值,从而达到提取更多细节信息的目的;文献[15]提出一种WKPCA人脸识别算法,通过将高、低分辨率人脸图像融合后形成新的图像特征进行识别;文献[16]提出一种GF的特征描述方法,使用梯度信息值进行特征提取;文献[17]提出一种CSGMP的识别算法,该算法首先将图像进行梯度转换,然后采用CS-LDP方法提取特征值,在一定程度上提升了识别率,文献[18]给出了计算图像梯度散度的、与坐标选取无关的简易近似公式,并应用到带噪数字图像中,利用梯度与散度的配合进行边缘提取。文献[19]针对人脸图像使用MCD算法,求出稳健的协方差矩阵估计,基于此协方差估计矩阵使用PCA技术提取重要的人脸特征用于识别。文献[20]对各类图形图像处理算法进行了总结与分析。文献[21-22]从提升算法抗噪性等方面着手优化了图像处理算法。
上述算法都能很好地解决人脸识别的问题,在识别率上有一定的改进与提升,但用于在脸部被遮挡情况下的识别时,上述算法在不同程度上存在耗时长常、识别不精确等缺陷;为了有效解决上述问题,本文提出一种可实现免脱帽人脸识别的身份识别算法,文中提出一种通过对图像偏移进行特征提取的算法,对一张图片的矩阵A分别向上、下、左、右方向偏移得到4个新的矩阵A1、A2、A3、A4,采用邻近空缺补偿将4个新矩阵的维度调整到至A的维度,然后用A分别减去上述矩阵,得到4个差额矩阵S1、S2、S3、S4,差额矩阵在不同方向上各自保留了图像的部分特征。对4个差额矩阵进行相关运算,可以得到描述更多特征信息的特征矩阵Sn,将矩阵Sn累加到图片A,产生新的对特征信息进行了强化的特征矩阵Sm,对矩阵Sm的亮点通过一定的算法进行调整,得到对图片A进行描述的特征矩阵Sfig。然后使用PCA技术对特征矩阵Sfig进行降维处理,获取到一定比例的有效信息,采用SVM向量机分类算法对各种不同条件下的人脸进行分类、识别,实验结果表明该算法在识别率提升的同时,其运行效率有非常卓越的表现。
经典LBP算法在人脸识别方向中的运行效率是学术界公认,而本文所述算法在确保识别率的情况下,其执行效率可以达到经典LBP算法执行效率的2倍以上。
1 本文算法
1.1 相关概念
1.1.1 图像梯度
一维函数的一阶微分定义为:
(1)
一个灰度图像,可以认为是一个二维函数f(x,y),分别对x、y求导即有:
(2)
(3)
因图像是离散的二维函数,ε不能无限小,而图像是按照像素进行离散,最小的ε就是1个像素。因此,对公式(2)、(3)进行转化,产生式(4)、(5)的形式(ε=1):
(4)
(5)
式(4)、(5)为图像g(x,y)点的水平梯度(x方向)和垂直梯度(y方向),从上面的表达式可以看出来,当ε=1时,图像的梯度相当于2个相邻像素的差值。
1.1.2 本文概念介绍
为演示偏移补偿法的基本操作,以中央为‘Z’型字母的7*7维矩阵A为例,演示偏移补偿算法的特征提取过程及最终效果图,过程如图1所示。
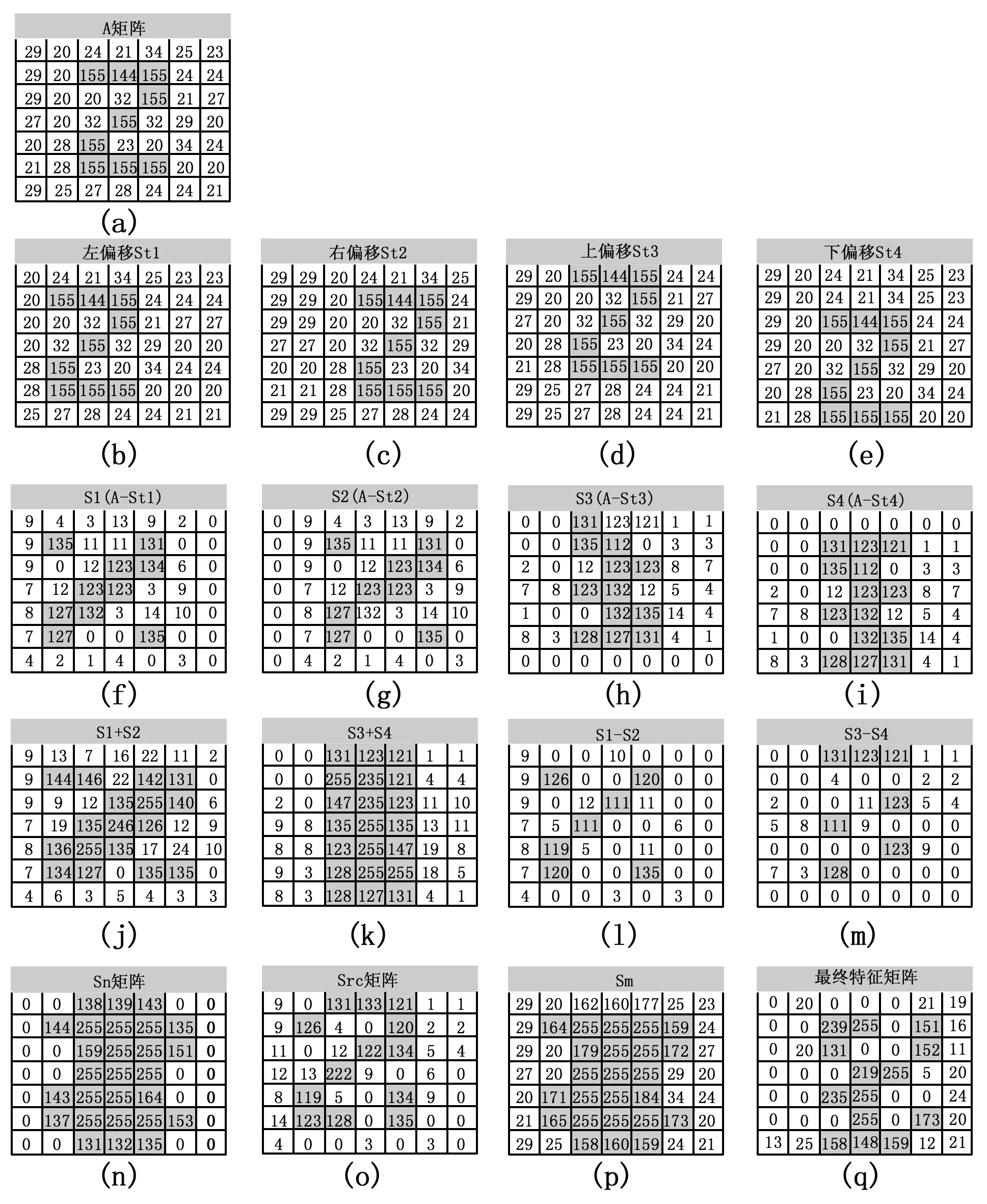
图1 Z形图像经过各种转化后的效果图
1)对矩阵A分别向上、下、左、右4个方向偏移1位,位数不足时,使用近邻填补法填充空矩阵,使其与A的维度保持一致,形成St1、St2、St3、St4四个偏移矩阵,见图1 (b)~(e);
2)用矩阵A分别减去St1、St2、St3、St4,产生S1、S2、S3、S4等4个差额矩阵,见图1 (f)~(i);
3)整理差额矩阵,形成纵方向、横方向上的特征矩阵,即Sz1=S1+S2、Sz2=S3+S4、Sf1=S1-S2、Sf2=S3-S4,见图1 (j)~(m);
4)组合差额矩阵,Sn=Sz1+Sz2、Src=Sf1+Sf2;对Sn进行均值降噪处理,此时Sn矩阵为对图片A特征扩大后的矩阵,可实现图片A的轮廓强化;矩阵Src提取了图片A轮廓的细节特征,见图1 (n)、(o);
5)将图片A矩阵与Sn矩阵相加,即Sm=A+Sn,产生一个强化了图片A轮廓特征的新矩阵Sm,见图1(p);
6)用矩阵Sm减去若干倍的Src,即Sfig=Sm-Src*r,Sfig即为图片A的特征矩阵,见图1 (q)。
1.2 算法流程
首先采用文章所推荐算法获取图像特征,然后使用3×3模板将第一步所得图像分解为若干子图,第三步对第二步所得的所有子图统计其直方图,得到特征向量,第四步使用PCA对所得进行降维,最后用SVM方法分类训练图像并完成识别[11],本文图像处理流程采用如图2所示。

图2 本文算法流程图
1.3 实施过程
将图片转化为灰度图,获得m*n阶矩阵A。
Step1:提取偏移矩阵
矩阵A的上偏移矩阵St1:
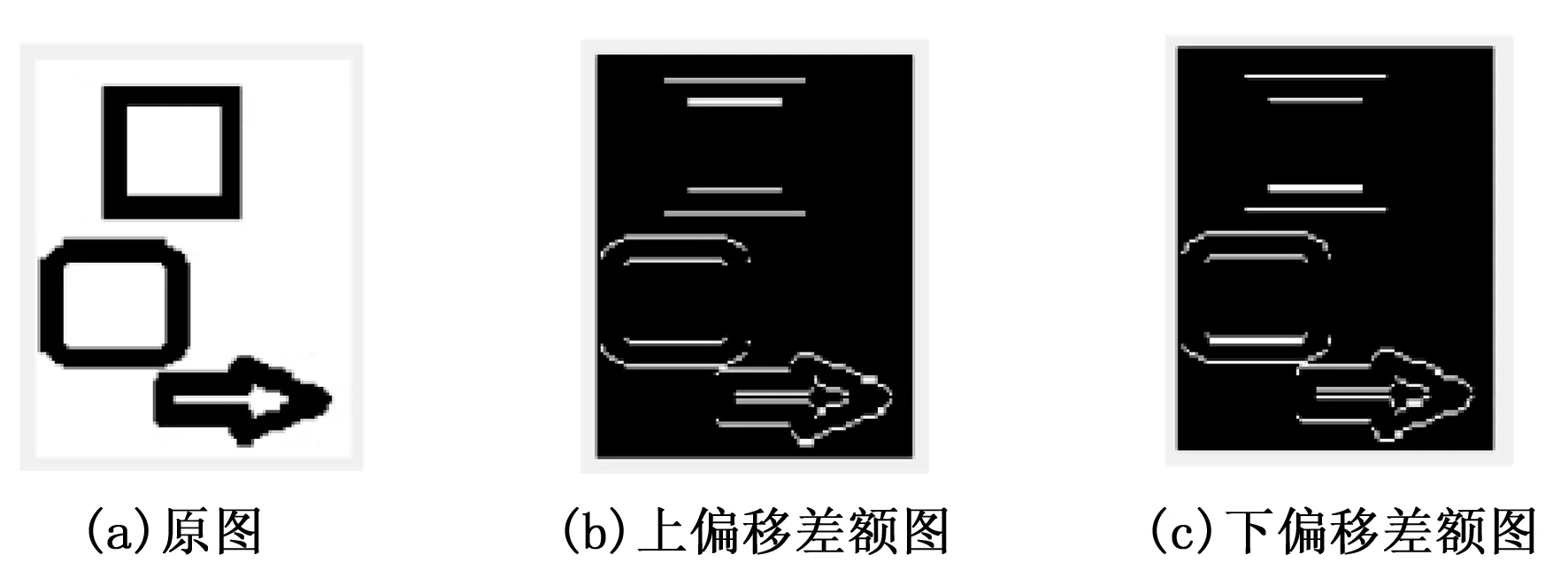
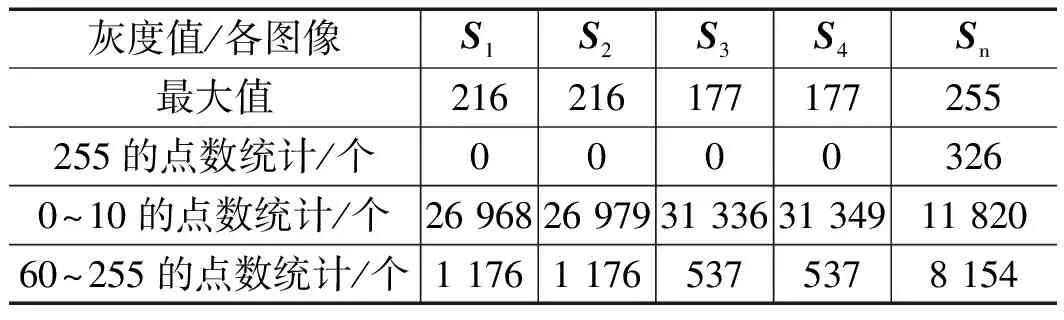
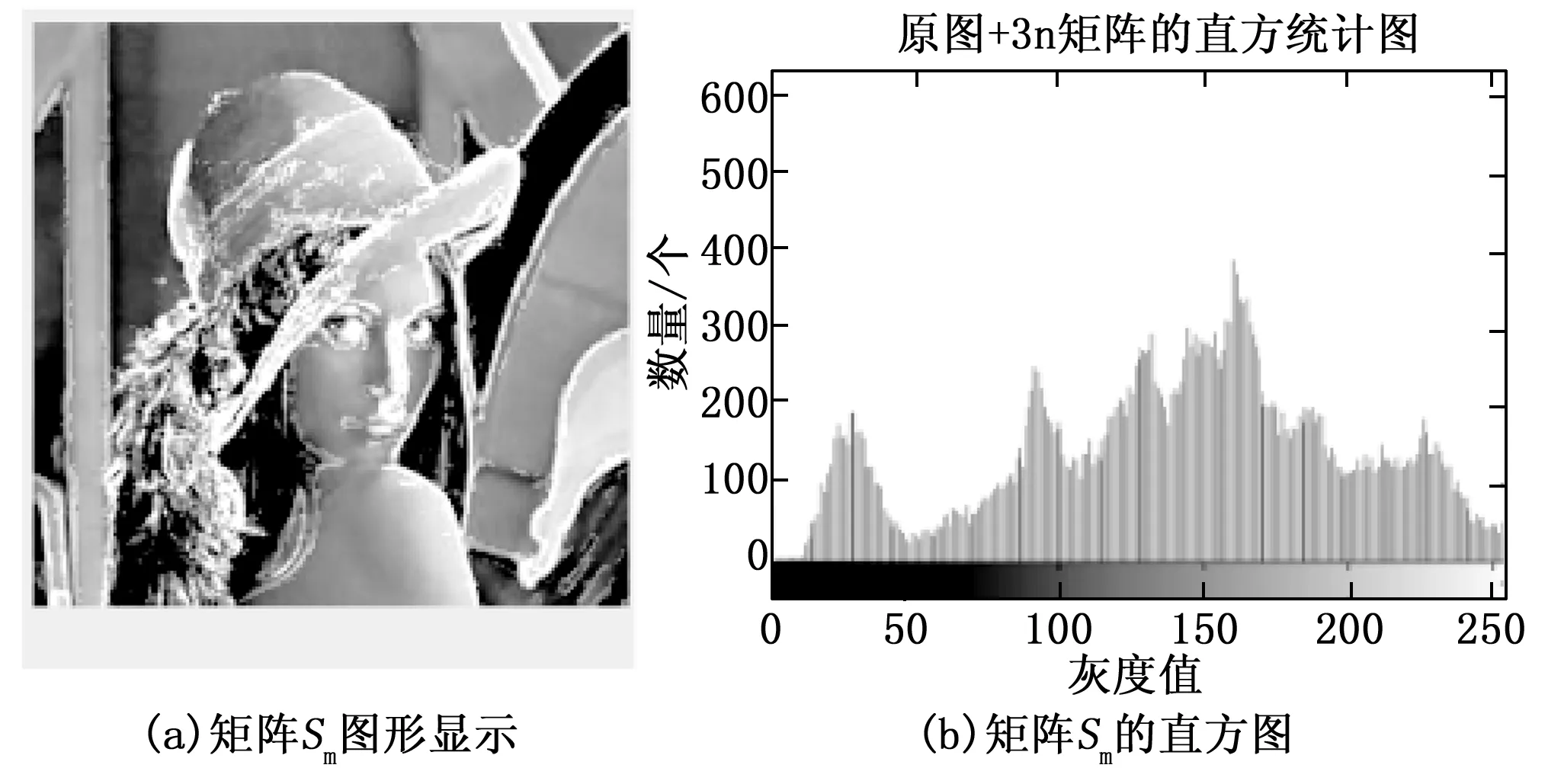
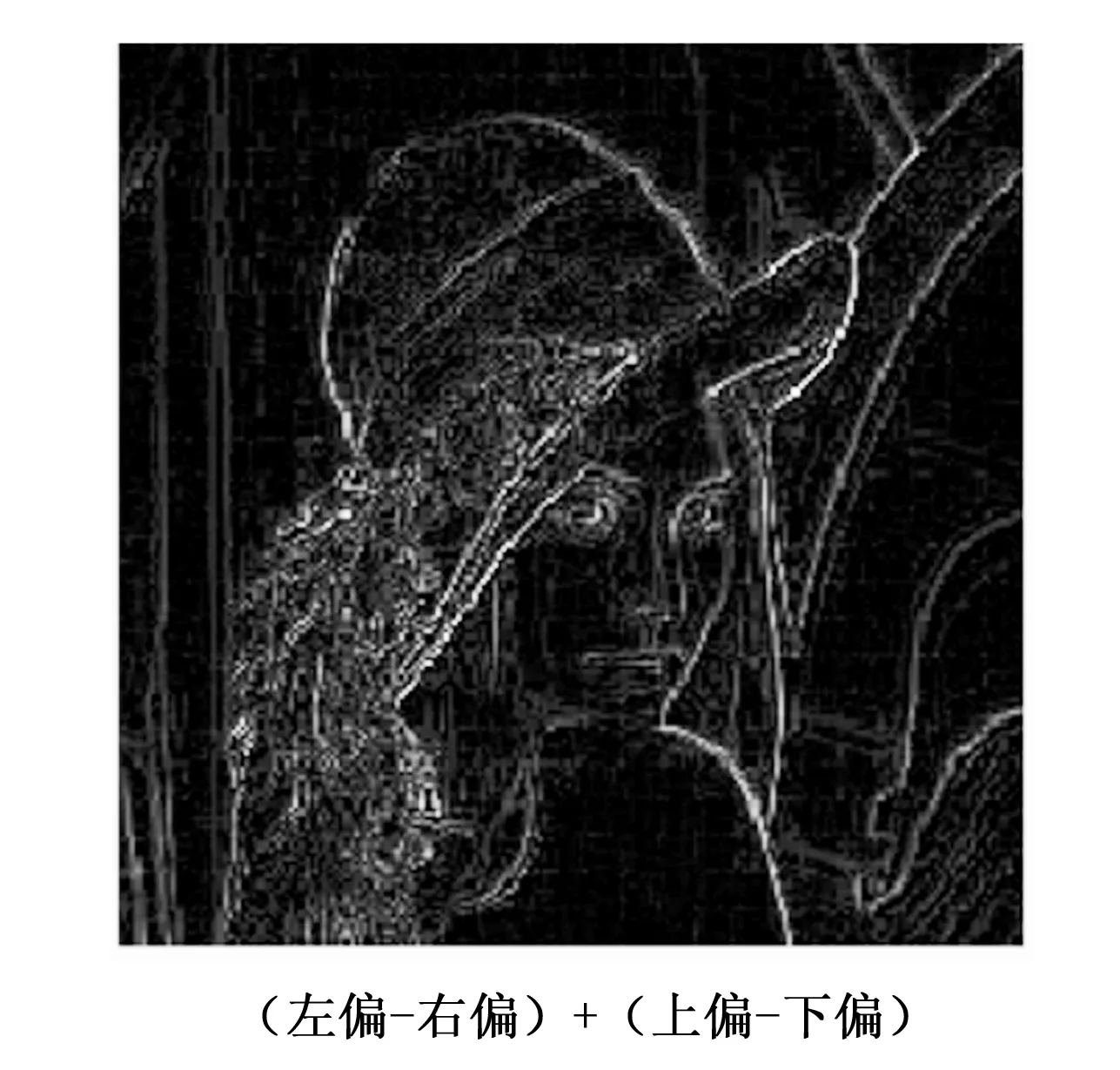
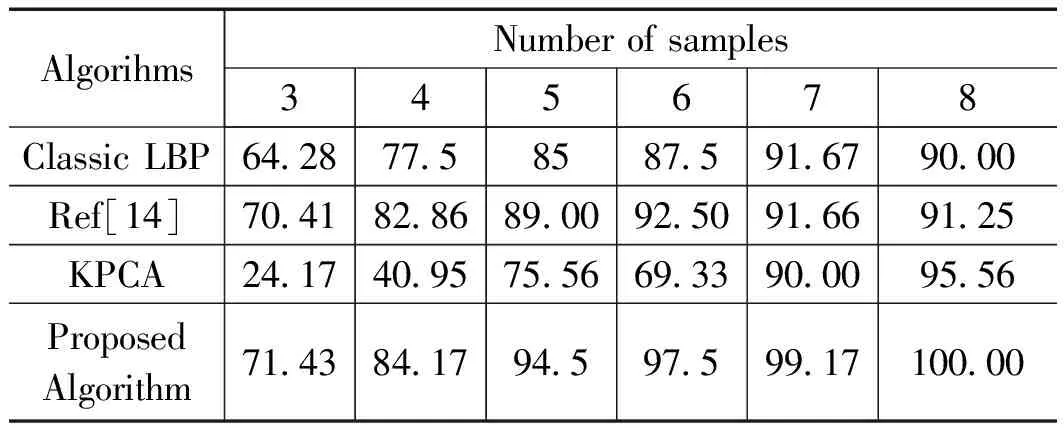
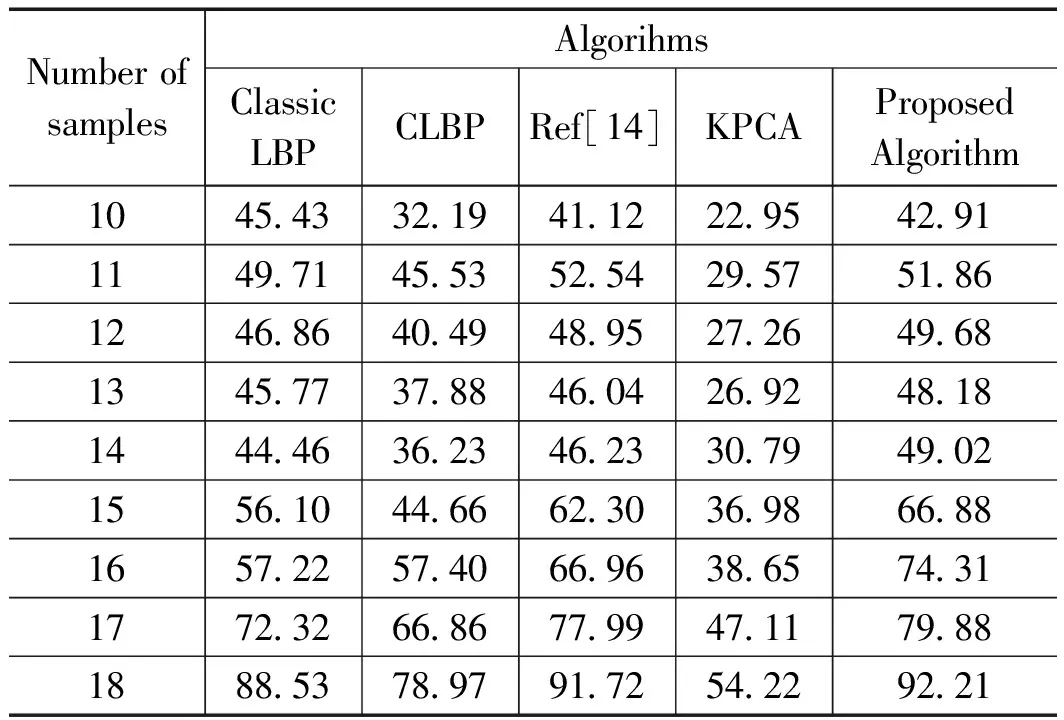
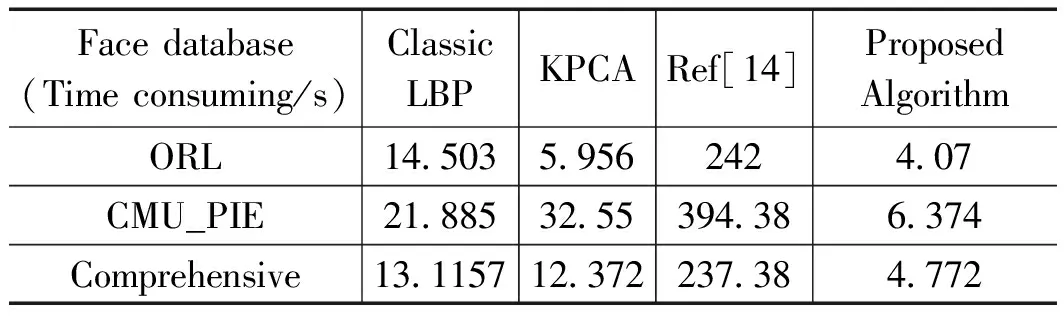
令i (6) 重复上述的方法,分别取得下偏移矩阵St2、左偏移矩阵St3、右偏移矩阵St4,其实现过程分别为: St2的实现公式: (7) St3的实现公式: (8) St4的实现公式: (9) Step2:获取差额矩阵 此时St1、St2、St3、St4为矩阵A分别向上、下、左、右移动一位之后的矩阵,其显示的结果几乎与原图相同,为了提取图形中的轮廓信息,我们令S1=|A-St1|,此时,如果矩阵A中的像素点a(i,j)与其上一行同列像素的值相同或者相近,运算后s1(i,j)的值为0或者一个非常小的数值,如果a(i,j)与其上一行同列像素的值存在较大差距,表明该像素点很有可能是图像的轮廓,该值经过绝对值运算之后为正数,能体现图像轮廓信息。通过对正方形等图形进行检测验证,我们发现,上、下偏移取差可以提取横向特征信息,如图3所示。同理,左右偏移取差可以提取纵向特征信息。 图3 图形在各方向上的梯度图像 用同样的方法分别获取S2、S3、S4几个方位的偏移差额图。其计算公式分别为: S1=|A-St1| (10) S2=|A-St2| (11) S3=|A-St3| (12) S4=|A-St4| (13) 对200*200像素的lena图像进行4个方向的转换,其结果如图4所示。 图4 Lena图片各方向的梯度图 Step3:合成Sn特征矩阵图像 为了得到图片更全面的轮廓信息,将上述4个矩阵进行累加,得到矩阵Sn。 Sn=S1+S2+S3+S4 (14) lena头像的Sn矩阵图像如图5所示。 图5 Lena的Sn矩阵图像 从图4可以看到,Sn图像的轮廓加宽的同时,亮度也增强了很多,将图片A的轮廓特征很好地显现了出来,对上述矩阵分析,对比结果如表1所示,其中B1、B2的最大灰度值为216,B3、B4的最大灰度值为177,经过累加后Sn的最大值为255,且255灰度值的总数量从0增长到326,同样,其他相同位置的像素值也在增加,可以解释亮度增强的原因;60~255像素点的统计数从0增加到了8 154,可以解释图形轮廓变宽的原因;同时因图片累加使用uint8数值进行运算,累加后超过255像素值的像素点,系统默认转换为255。 表1 Sn图像运算后像素值 Step3:对Sn矩阵进行降噪处理 仔细观察Sn图片及矩阵发现,Sn中存在较多的散点,这些散点大多并非图片轮廓相关的特征信息,为了剔除散点的影响,我们使用适当算法对该矩阵进行降噪处理。本文采用均值法,其算法为: (15) 其中:mean为矩阵Sn的灰度值均值。 通过上述算法,去除部分散点,能更好地凸显图像的轮廓及纹理特征。 Step4:将Sn矩阵与原灰度图矩阵A进行累加 Sn矩阵较好地提取了图片A的轮廓等特征信息,以图像lena为例,对Sn矩阵分析发现,灰度值为0的像素点统计数为27 357,占比达到68.4%,远大于等于均值的像素点数为12 643个,因为像素点数分布不均匀,不太适合直接用做图片特征值。我们将Sn矩阵与原灰度图矩阵A进行累加,获得新的矩阵Sm。 Sm=A+Sn (16) 其图形显示及直方图分别如图6所示。 图6 Sm图及对应直方图 矩阵Sm有以下几个特点:1)像素点相对均衡;2)强化了图片中能代表图片特性的轮廓特征;3)255像素点附近的数量增多,这是因为在原矩阵A上增加了Sn矩阵,导致图片轮廓附近的像素值达到最大值255,从图片中的亮点也可以看到。 因为对图片的训练、识别要用到直方图特性,而255像素点附近的像素点数量增多,会在一定程度上会降低图像的识别率,为了进一步提高图片识别率,需要通过一定途径进一步降低图片中255像素点的数量。 Step5:提取纵、横方向上的细微特征 对上、下方向上的两个差额矩阵S1、S2进行相减,得到矩阵Sr,可以保留纵向(Y轴)上更细微的局部特征。 Sr=S1-S2 (17) 对左、右方向上的两个差额矩阵S3、S4相减,得到矩阵Sc,保留横向(X轴)上细微的局部特征。 Sc=S3-S4 (18) 将Src=Sr+Sc,可以得到图片水平、垂直方向上的综合细微特征图,lena图像的Src图像显示如图7所示。Src相对Sm而言,提取的信息更加细腻,而Sm的特征信息更加粗犷。 图7 Src矩阵的图形 Step6:获得取图片的特征 对比step4的结果Sm和step5的结果Src,在Sm图像中,有部分亮点的像素值超过255,使用Src对Sm图像亮点部分的像素值进行适当的减弱,增强图片的特征。因Sm是由原图A叠加Sn而来,Sn体现的是图片粗狂的轮廓信息,而Src能体现图片更细微的轮廓特征,用Src对应位置的像素值来减弱Sm的亮点,可以有效降低亮点的数量,增强图片的可识别性。我们令Sfig=Sm-Src*r,即对Sm矩阵减若干次Src,r可取实数。实验证明r取4~10范围内的数字时,识别效果较好,图8是r=5时对应的图片效果。 图8 本文算法特征图 Sfig矩阵即为图片lena的最终特征值,该图保留了原图更多的细节特征,有利于图片的识别。 Step7:将所获取的特征图片进行均等分块,对每个分块的图片进行直方图统计,然后按照一定的次序将各个分块的直方图进行链接,形成特征向量,本文对特征图的分块方式采用3×3模式。 2.1.1 实验环境 本文试验操作平台硬件配置为:CPU四核 i3-2370M,主频2.4 GHz,内存8 G(其中显存分配1 G),Win7旗舰版64位操作系统,仿真软件选用Matlab 2016a,实验数据使用ORL人脸数据库完成测试。 2.1.2 参数设置 图像分块模板采用3×3的模板,分类器使用台湾学者林智仁教授团队开发的LibSVM分类器,其对应参数设置为‘ -s0-t2-c16-g0.0009765625’。 2.1.3 图像遮挡处理方法 为了对比算法在有遮挡物情况下的识别率,采用一款如图9(a)所示规格为92*35的遮挡图对原图的面部上部做遮挡处理,如图9所示,图2(c)为遮挡完毕后的图像。 图9 采用遮挡图对人脸进行遮挡的处理 为了验证本文所述算法的有效性,分别在ORL、CMU_PIE人脸集上与经典LBP、文献[15]所述的KPCA、文献[14]所述等优秀算法进行识别率结果的对比分析。 2.2.1 识别率分析 为验证本文算法在识别率方面的表现,对所参考的算法,若原文献中提供实验参数,使用原文参数,原文未提供实验参数的,使用与本文相同的参数进行设置,为更充分地比较各算法,研究者分析了所测数据库上每个人训练图像数占个人图像总数的30%~80%之间的所有情况,以便更全面地分析各算法识别效果。 2.2.1.1 ORL数据库测试结果 ORL人脸数据库是由英国剑桥大学的Olivetti研究实验室创建,该数据集包含40个人,每人10张照片,其中包括了表情变化,微小姿态变化,20%以内的尺度变化,其规格为92*112。本实验中,所有图片都使用2.1.3所示的方法进行遮挡处理,分别使用数据库中每人的前3幅图像至前8幅图像进行训练,其他剩余图像用于测试,其测试结果如图10和表2所示。 从表2可以得到,在ORL人脸数据库中,文献[14]算法、KPCA算法及本文算法都有较好的表现,但本文算法相对而言表现更优;文献[14]算法在使用6张以上的训练图时,取得超过92%的识别率。KPCA算法在使用8张训练图时取得95%左右的识别率,在使用7张及以下的训练图时,其识别率效果欠佳。本文算法展示的识别率在使用各个不同训练图片时,其识别率均高于文献[14]等对比算法。 表2 ORL库中各算法在不同数量训练图片下的识别率 % 2.2.1.2 CMU_PIE数据库测试结果 CMU_PIE人脸数据库是由卡耐基梅隆大学创建,该数据集原始数据库包含68个人,原数据库包含每人的13种姿态条件,43种光照条件和4种表情下的照片,总计40 000张照片,因原数据库图像较大,本文使用其中每人24幅不同光照、不同角度状态下的图片,共计1 632张人脸图进行测试,其图片采用64×64规格的灰度图像。本实验中,分别使用数据库中每人的前10副图像到前18幅图像进行训练,其他剩余图像用于测试,其测试结果如表3所示。 表3 CUM_PIE库中各算法在不同数量训练 由表3分析得到,在CMU_PIE人脸数据库中,LBP算法在训练数为10时,文献[14]算法在训练数为11时,识别率略高于本文算法,除此之外,本文算法的识别率均优于其他被参照算法,在训练图片的数量为18时,本文算法的识别率可以达到92.21%。 综上所述,对本文所述算法分别在ORL人脸识别库、CMU_PIE人脸识别库上与经典LBP算法、CLBP算法、KPCA算法、文献[14]算法等进行对比,本文算法在识别率上的综合表现,优于其他算法。 2.2.2 时间复杂度分析 为了对比不同算法的计算效率,记录了经典LBP算法、KPCA算法、文献[14]算法及本文算法在同等软硬件条件下提取ORL数据库、CMU_PIE数据库所有图像特征图所消耗的总时长,其结果如表4所示。 表4 各算法运行效率分析 分析表4可知,在在ORL人脸识别库中,运行效率相对较好的算法依然是KPCA算法,其提取ORL数据库400张92*112规格图像的特征信息,使用了5.956 s,他们的运行效率是经典LBP算法的2.44倍,是文献[14]算法运行效率的40.6倍,但相对本文算法耗时4.07 s而言,KPCA算法的运行效率还是相对较低; 在CMU_PIE数据库上,表现相对较好的算法是CLBP算法,他们在提取CMU_PIE数据库1 632张64×64规格图像的特征信息,分别使用了21.885 s,在ORL数据库中表现较佳的KPCA算法,在提取CMU_PIE数据库特征信息时,表现的并没之前展现的那么优秀,提取特征信息总耗时32.55 s,研究者多次运行验证,未能得到之前展现的效果;而本文算法总耗时为6.374 s。综合提取3个数据库图像特征的平均耗时,本文算法为4.772 s,远远高于其他算法的运行时间。 从实验结果可以看到,所述算法的识别率表现优于其他对比算法,说明本文所提供算法在被识别人员带帽或部分面部被遮挡情况下进行身份识别时具有很高的识别率,能够满足免脱帽进行身份识别的需求。 为了解决面部被遮挡情况下人脸识别系统识别率低,在识别时强行需要被识别人员去除帽子、头盔等操作所带来的不便及安全隐患,本文提出一种使用图像多方位梯度,通过融合、补偿方式产生可以对原图像进行特征描述的特征图,通过对该特征图进行分块统计、主成分分析,采用SVM分类器进行分类并进行识别的算法,算法可以实现在免脱帽情况下的高识别率,通过大量仿真实验表明,本文所述算法在ORL等人脸数据库中,取得优秀识别率的同时,在识别效率上同样具有非常卓越的表现。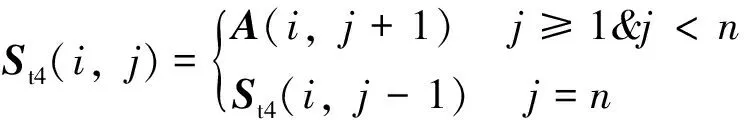


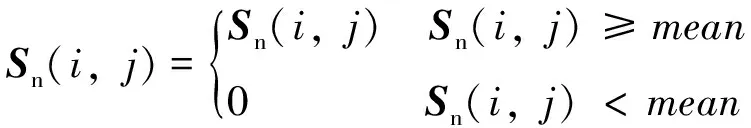

2 实验与结果分析
2.1 实验设置

2.2 实验结果
3 结束语

