中国大陆速度场在CGCS2000坐标转换中的应用研究
王建红 李涌涛 马洪磊
1 中铁第一勘察设计院集团有限公司,西安市西影路2号,710043 2 西安测绘总站,西安市西影路36号,710054 3 信息工程大学地理空间信息学院,郑州市科学大道62号,450001
1 欧拉矢量法速度场建模
根据欧拉定理,将地球近似为球体,对于变化速度单位为cm/a的板块运动来说,地球半径变化可忽略不计。则欧拉矢量可表示为[9]:
V=Ω×r
(1)
式中,V为块体内某点的运动速度,Ω为该点的欧拉矢量,r为该点的矢径。欧拉定理在空间直角坐标系中的表示形式为[8]:
(2)
式中,Vx、Vy、Vz为该点在地心坐标系下的速度,(x,y,z)为该点的地心坐标,Ωx、Ωy、Ωz为欧拉矢量的3个分量。
2 速度场内插方法
2.1 最近邻点插值法
最近邻点插值法的原理为任意网格点的属性值与其几何位置最近点的属性值相同,即将每一个网格节点的最近邻点Lmin(xi,yi,zi)值作为待求点L(x,y,z)的节点值,其插值如下[7,10]:
VL=Vdi(min)
(3)
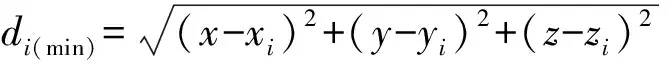
2.2 反距离加权法
反距离加权法是一种加权平均插值法。设在空间分布一系列离散点W(x,y,z),已知待插值点坐标为W(xi,yi,zi),根据周围离散点数值Zi(i=1,2,…,n),通过距离加权插值法求得W点数值为[7]:
(4)
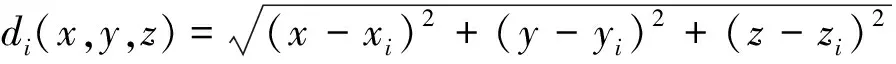
2.3 格网内插法
利用已建立的N°×N°速度场格网模型,选取未知点邻近的4个格网点进行双线性内插,从而得到未知点速度(图1)。格网双线性内插公式为:
00后大学生早已在电视和网络媒体蓬勃发展的时代下“游刃有余”,对他们而言在开展心理健康教育时极度挑剔教育形式,传统的说教式教学不仅收效甚微,还会引起学生反感和憎恶,而最适宜的则是借助于心理学知识相关的视频材料或时事热点来进行论述。比如教师可组织学生观看02年的“马加爵事件”及相关分析讨论,继而引导学生体会不良情绪累积的危害性,再顺利渗透自我调节的科学方法。
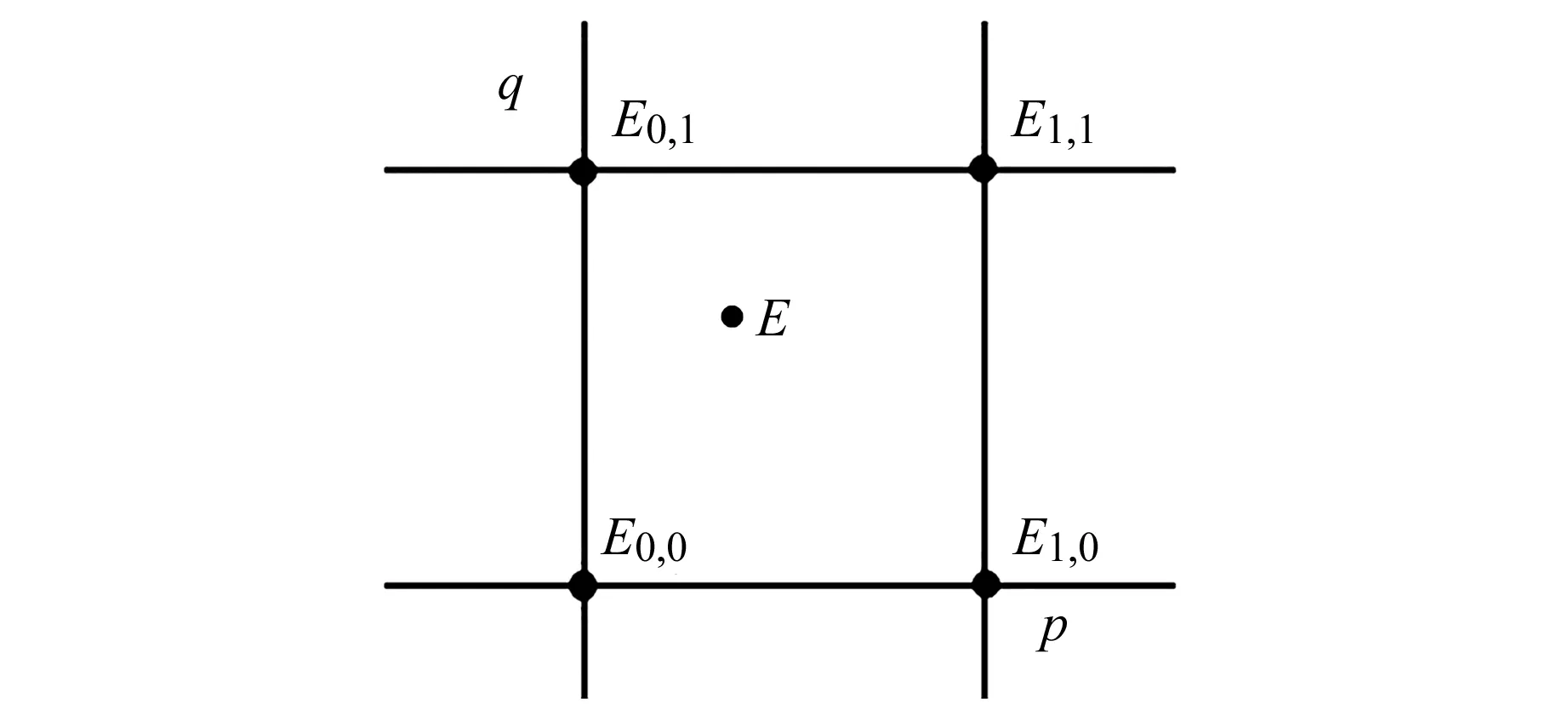
图1 格网双线性内插
VE(λ0+pΔλ,β0+qΔβ)=(1-p)(1-q)VE0,0+
p(1-q)VE1,0+q(1-p)VE0,1+pqVE1,1
(5)
式中,0≤p<1,0≤q<1,Δλ和Δβ分别为经线和纬线方向上的格网宽度。
3 CGCS2000坐标转换中历元归算方法
CGCS2000历元归算可根据相应的速度场模型将测站观测历元的坐标归算至2000.0历元上。任意历元T1的站点坐标转换至2000.0历元可表示为[11]:
(6)
式中,T1为观测历元,VX、VY、VZ为测站在ITRF框架下的速度。
4 速度场建模与应用分析
4.1 速度场格网模型建立
利用中国大陆2013~2019年2 074个GNSS站观测数据,以中国周边16个IGS站为基准进行单日解算和网平差,得到每个测站的单日解,并通过对测站坐标单日解时间序列进行一元线性回归解算得到各测站速度。
根据实际解算的2 074个测站速度数据建立不同方法、不同分辨率下的中国大陆速度场模型。速度场格网模型建立步骤如下:1)将经纬度范围(72°~135°E,18°~54°N)按3°×3°空间分辨率分为137个格网;2)利用每个格网中已知速度的测站,根据最小二乘原理及式(2)计算每个格网的欧拉矢量;3)采用式(2)计算格网中心点速度并作为该格网的速度(中心点格网速度场);4)采用式(2)计算每个格网点的速度,并取相邻4个格网点的平均值作为该格网点的速度(4点格网速度场),用于格网内插。
本文建立的中心点格网速度场与文献[4]对应的格网速度差值及统计值如图2和表1(单位mm/a)所示。
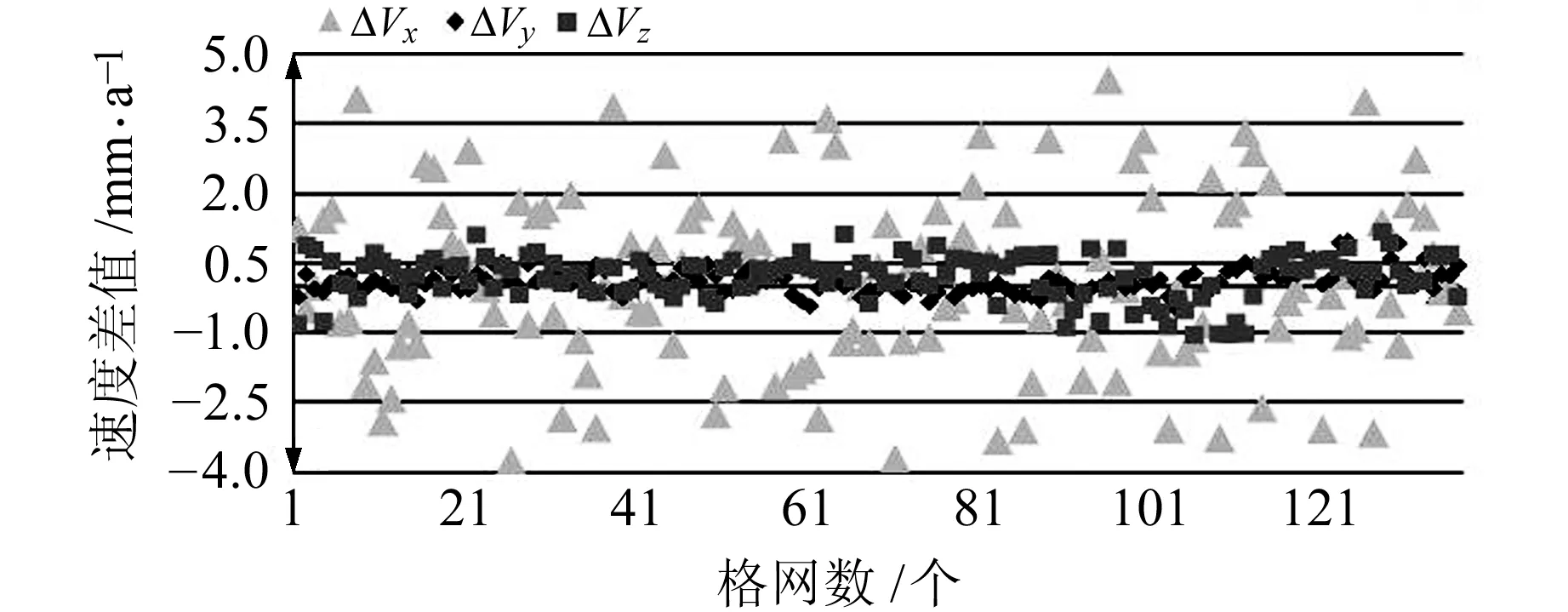
图2 中心点格网速度场速度差值
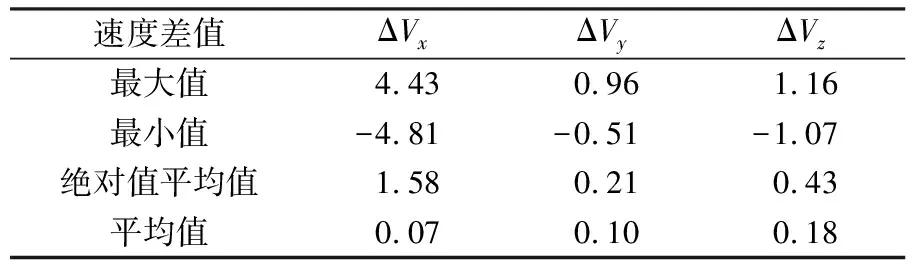
表1 中心点格网速度场速度差值统计
由图2可知,两个格网速度场中X方向的速度差值比Y和Z方向大一个量级,其原因为X方向速度比Y和Z方向大一个量级,相同量级的速度作差后其差值也相差一个量级。由表1可知,两个速度场对应的每个格网中X、Y、Z三个方向差值的最值、平均值和绝对值平均值,相对其3个方向的平均速度(-31.72 mm/a、-6.42 mm/a、-9.6 mm/a)[4]差异较小。总体而言,两个速度场模型精度相当,进一步证明本文建立的速度场具有可靠性。
4.2 速度场在历元归算中的应用分析
统计2 074个测站实测速度与其所在中心点格网速度场的速度差值,结果如图3和表2(单位mm/a)所示,从2020.0历元归算至2000.0历元的坐标差值如表3(单位cm)所示。
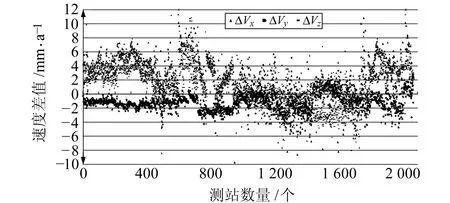
图3 2 074个测站实测速度与其所在中心点格网速度场速度差值
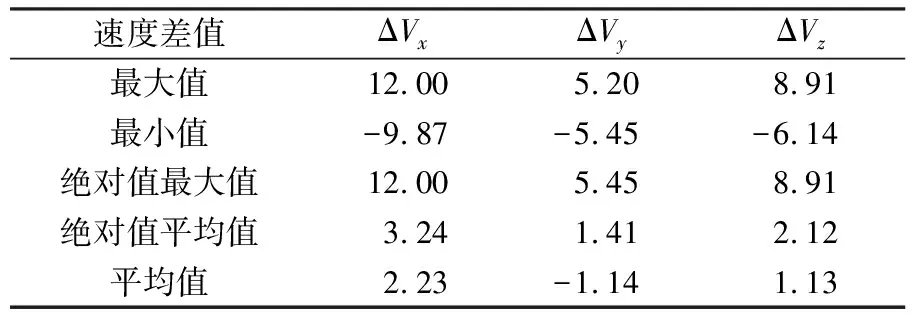
表2 2 074个测站实测速度与其所在中心点格网速度场速度差值统计
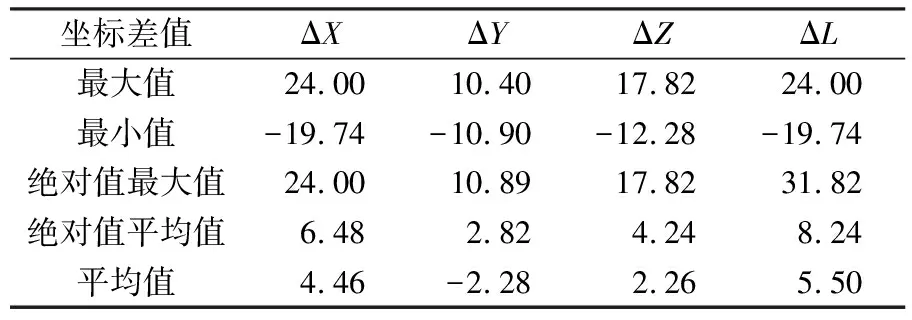
表3 采用实测速度与中心点格网速度场对2 074个测站历元归算(2020.0归算至2000.0)后的坐标差值统计
由图3和表2可知,2 074个测站实测速度与中心点格网速度场速度存在明显差异,X、Y、Z三个方向的最大值分别为12.00 mm/a、5.45 mm/a和8.91 mm/a,这是由于格网分辨率过大且欧拉矢量法建模存在一定精度限制所致。平均值和绝对值平均值较小,说明格网模型具有一定的合理性和有效性,能满足普遍情况下的历元估算精度。
由表3可知,在从2020.0历元归算至2000.0历元时,平均值和绝对值平均值较小,说明利用速度场模型进行历元归算的普适性较好。测站较少区域的速度场模型精度有限,因此历元归算精度也偏低。速度间差异导致X、Y、Z三个方向的坐标差异最大达24.00 cm、10.89 cm和17.82 cm,空间三维误差达31.82 cm,表明不同测站的坐标均存在不同程度的差异,且随着时间增加差异逐渐增大。
利用本文建立的3°×3°中心点格网速度场对2 074个测站实测速度进行历元归算。为减小历元归算误差、提高归算精度,基于本文建立的3°×3°格网速度场和2 074个测站实测速度两类数据,充分考虑两者的实际有效性和适用范围后,根据每个待求速度测站周围的已知速度的测站个数及待求速度测站与已知速度测站之间的距离,采用不同方法进行速度内插,以提高历元归算精度。不同内插方法适用表见表4。
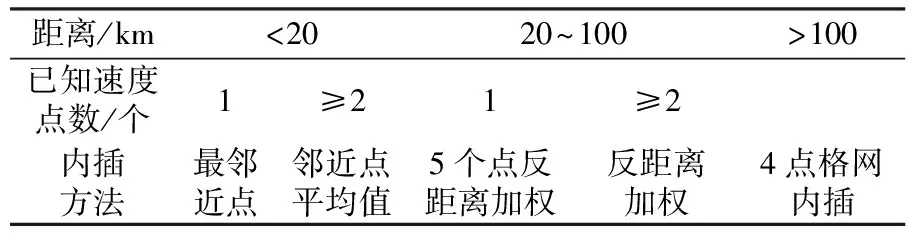
表4 不同内插方法适用表
在2 074个测站中任意选取5个测站,在数据库中删除这5个测站的实际速度数据,其实际速度如表5(单位mm/a)所示。将5个测站作为未知速度测站,比较采用表4中内插方法计算的测站速度值与实际速度值的差异,结果如表6(单位mm/a)和图4所示。
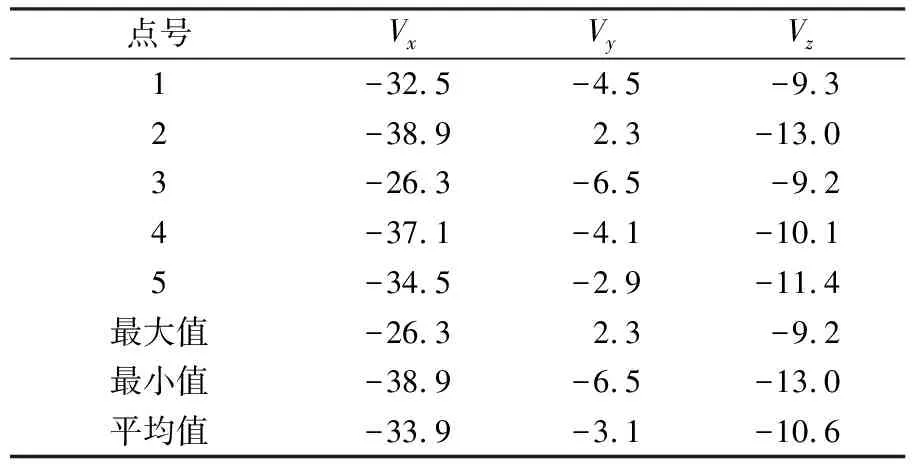
表5 5个测站的实测速度
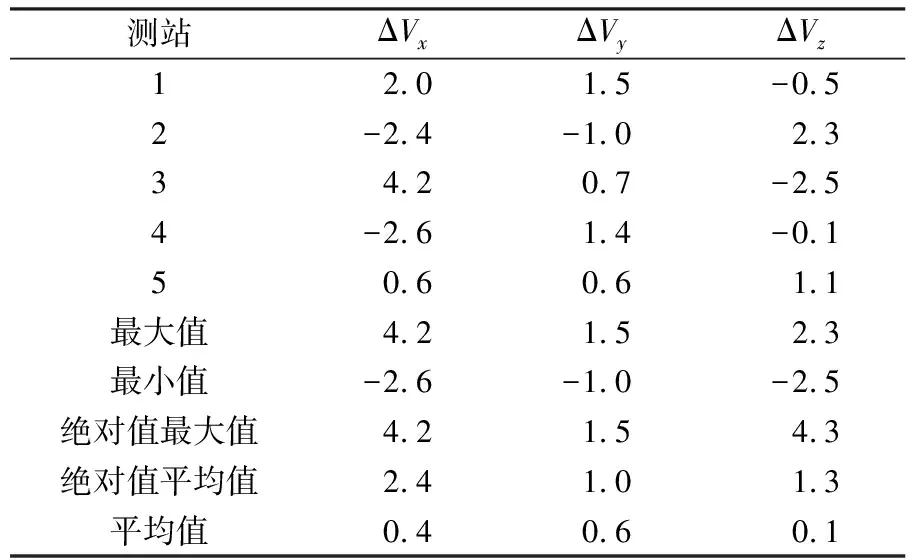
表6 5个测站实测速度与不同内插方法组合速度差值统计
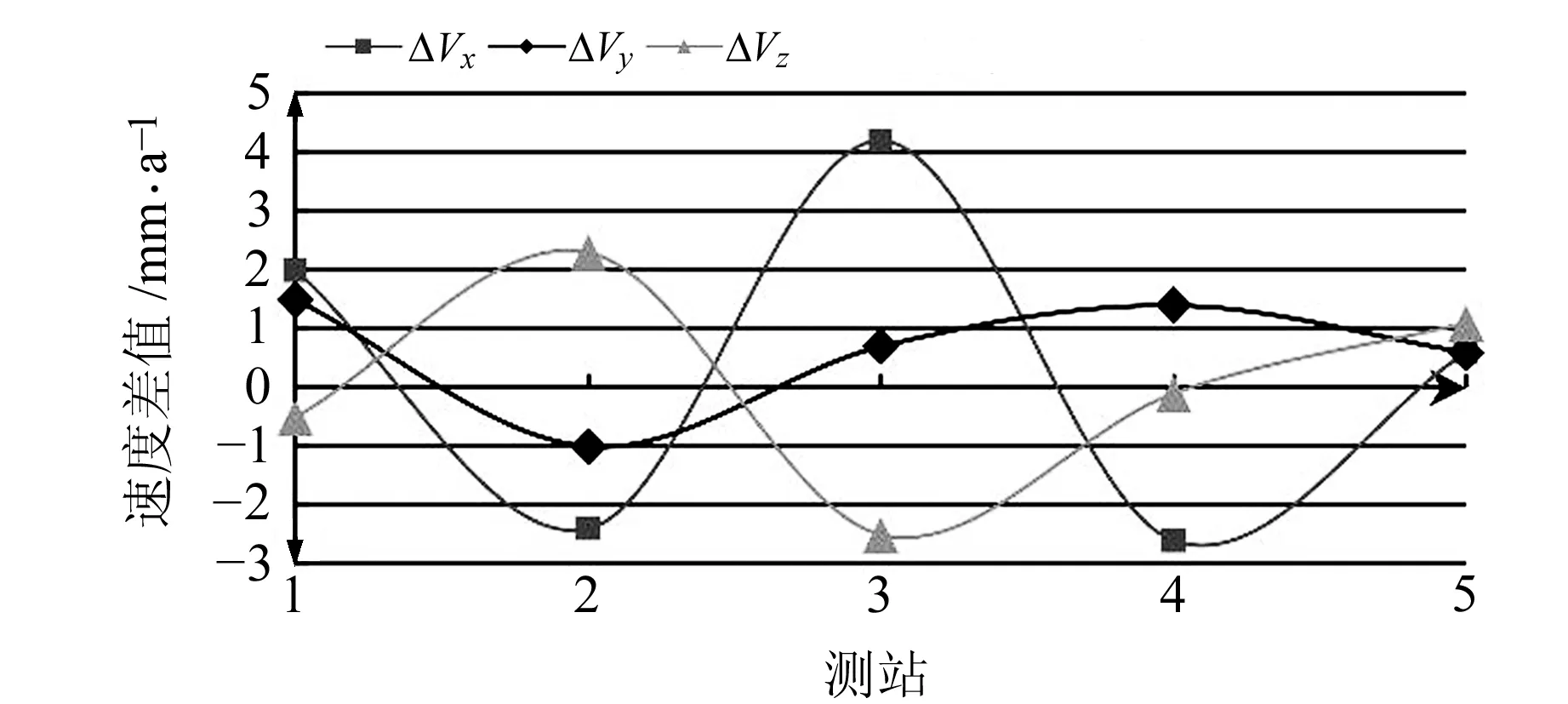
图4 5个测站实测速度与不同内插方法组合速度差值
由表6和图4可知,根据3°×3°格网速度场和2 074个测站的已知速度,采用不同内插方法得到的速度与5个测站的实测速度在X、Y、Z三个方向上差值的绝对值平均值分别为2.4 mm/a、1.0 mm/a和1.3 mm/a,两者差异较小,且差值平均值均小于1 mm/a,表明不同内插方法组合计算的速度更接近实际速度。通过对比表6和表2可知,充分利用2 074个测站的实测速度并组合不同内插方法计算得到的测站速度,相比于格网速度场模型速度具有更高的精度,且更接近实际值,可达到进一步提高历元归算精度的目的。
5 结 语
速度场精度会直接影响CGCS2000坐标系历元归算的精度,即点位坐标在CGCS2000坐标系中的精度,而单纯采用速度场模型进行的历元归算,未顾及小范围内板块相对运动较小的特点以及在已知速度测站较少的区域内建立的速度场模型精度存在局限性。基于上述原因,本文在充分利用已知速度的测站并结合4点格网速度场模型的前提下,根据不同区域范围,组合利用最邻近点插值、反距离加权和格网内插3种方法对区域内未知点速度进行历元归算。结果表明,组合不同内插方法可合理利用不同范围和不同情况下区域内已知的测站速度,相比于单纯利用速度场格网更加科学合理,可使整体归算精度得到较大幅度提升,在X、Y、Z三个方向上的历元归算精度最高可提高24.00 cm、10.89 cm和17.82 cm,对不同情况下利用已知速度的测站提高历元归算精度具有一定指导意义。

