含裂纹砂浆试件的非共线混频超声试验研究
刘剑锋, 汪 魁,*, 彭爱红, 赵明阶
(1.重庆交通大学水工建筑物健康诊断技术重庆市高校工程研究中心,重庆 400074;2.江西省交通工程集团有限公司,江西 南昌 330000)
超声波与损伤处的非线性力学行为可以借用非线性超声波来表达,根据探测信号的频率变化等数据可实现损伤检测.根据检测分析原理的不同,非线性超声可分为高次谐波法、混频法、振动调制法等.其中,根据2 列入射声波入射方向是否平行,非线性超声混频法可分为共线混频法和非共线混频法.由于非线性超声非共线混频法频率可选择,检测位置可确定,对损伤敏感性较强,能较好地避免非线性源的干扰等优点,因此有着很好的发展潜力.
从1960 年以后,就有相关研究人员[1-2]注意到在各向同性固体中,弹性波的相互作用以及岩石中非线性效应的产生.焦敬品等[3-4]运用非共线混频法检测了含有闭合裂纹的钢质梁.刘斯明等[5]针对铝合金试样以及SiCp/Al 复合材料进行非共线混频检测试验,验证了非共线方法的可行性.Croxford 等[6]利用非共线混频法对Al试件塑性变形和疲劳损伤情况进行了检测.Sun 等[7]针对铝合金试件,通过数值模拟和试验验证了非线性系数与2 列入射横波夹角的关系.Demcˉenko 等[8]采用线性超声波等常规超声检测技术和非共线超声混频技术进行了对比试验.Blanloeuil等[9]利用有限元模型,研究了平面弹性波与不同方向裂纹的相互作用.Pecorari 等[10]利用赫兹接触模型,分析了平面波与2 个粗糙表面之间的非线性作用.
上述研究表明,非线性超声非共线混频法在金属材料领域已有一定的研究成果,而且该方法具有方向可控、频率可选、灵敏度高等显著优点,在混凝土等非均质材料的检测应用中具有巨大潜力.但该方法的理论基础、测试系统、结果的可靠性还有待进一步开展研究,因此本文针对含裂纹水泥砂浆试件,进行非线性超声非共线混频法检测试验研究,讨论混频法非线性系数与裂纹长度和角度变化之间的关系,并与高次谐波法的试验结果进行对比,验证非共线混频法的可行性.
1 非线性超声非共线混频法基本理论
根据非线性超声理论,当2 列波相交区域含有损伤时,将出现非线性源,此时线性叠加原理不再满足,散射出频率为ω1±ω2的第3 列波,即混频波[11].进一步,根据一维非线性波动方程,在泰勒展开式中只保留2 阶非线性项,应用微扰理论,得出其解为[12]:

式中:u0是线性解;u1是非线性解;β为混频法非线性系数;A1和A2、ω1和ω2分别为2 列入射基频波的幅值和频率;k1、k2对应基频波波数.由此可得β的表达式[12]:

式中:A-、A+是混频波分别为差频、和频时的幅值.
由式(2)可知,β不仅与材料损伤程度有关,还与传播距离和波数有关.其中波数由信号发生器设定,传播距离恒定或设为固定量.为方便分析,式(2)可简化为:

由式(3)可知,混频法非线性系数与基频波振幅成反比,与混频波振幅成正比.
结合裂纹处接触的应力-应变关系,利用泰勒公式,根据赫兹接触模型理论,即超声波传播到裂纹处时,垂直于裂纹方向的声波分量会促使裂纹发生一拍一合的“拍击效应”,最后得到混频信号分量位移场,将其代入非线性系数表达式(3),可得到如下表达式[13-14]:

式中:θ为裂纹与超声波传播方向的夹角;D为裂纹长度;S为微裂纹横截面积;A3、k3分别为混频波的振幅和波数;L为试件长度.
由式(4)可知,混频法非线性系数β与sinθ和D2成正比,即β关于θ和D呈正相关关系.
2 非共线混频测试系统
2.1 测试装置组建
试验系统包括信号发生器DG1022U、放大器ATA-2042、示 波 器TBS1072B、换 能 器(发 射 端PXR04、PXR07,接收端PXR50);信号发生器设置发出2 列正弦波基频波.试验系统示意图见图1;换能器参数见表1,表中频率带宽表示换能器激发频率的范围,谐振频率表示换能器能激发的中心频率.

表1 换能器参数Table 1 Transducer parameters

图1 非共线混频测试系统示意图Fig.1 Schematic diagram of non-collinear mixing test system
2.2 非共线混频法的验证
本试验采用2 列横波谐振混频成第3 列纵波形式,对砂浆试件进行检测,根据谐振条件[1],生成频率为ω1+ω2的第3 列混频波.结合谐振条件、Snell 定律以及数学几何运算可得到2 列入射基频波的频率比ω2/ω1与入射角度θP1、θP2的关系式为:

式中:vPP是纵波在有机玻璃中的传播速度;vSC和vPC分别为横波和纵波在混凝土中的传播速度;d是频率比ω2/ω1.
为方便试验设计以及对比,借助Matlab 软件分析得到2 列入射基频波频率比与其夹角的关系曲线,结合式(5)、(6),得到频率比d为0.83 时,相应的2 列波的入射角度分别为52°和71°.
通过调节信号发生器通道1 和2 来验证生成混频的效果:(1)通道1、2 各自单独激发;(2)通道1、2 单独激发后再叠加;(3)通道1、2 同时激发.换能器接收经由示波器显示出的超声信号见图2.由图2(a)~(d)可知,其振幅峰值分别为0.134 0、0.050 4、0.173 6、0.182 0 V,即双通道同时激发的振幅峰值大于双通道各自单独激发以及单独激发后再叠加的振幅峰值,说明双通道同时激发谐振生成的混频波具有明显的非线性效应.为了排除基频信号以及其他非线性源的干扰,增大混频效应,将双通道各自单独激发后再叠加的信号与双通道同时激发时的信号相减得到增强混频信号,其时域和频域分析结果如图3、4 所示.为避免非线性测量的不稳定性,选取时域图中前7 个波进行频域分析.由频域图(图4)可以看出,出现了频率为40、48 kHz 的基频信号,即A2和A1;同时也含有频率为88 kHz 的混频波和频信号A3,从而证明了非共线混频法的有效性.

图2 PXR50 换能器接收的超声信号Fig.2 Ultrasonic signal received by the PXR50 transducer

图3 信号相减后的时域图Fig.3 Time domain diagram after subtraction

图4 信号相减后的频域图Fig.4 Frequency diagram after subtraction
3 非共线混频试验
3.1 试件制作
本试验砂浆试件采用42.5 级普通硅酸盐水泥,设计满足GB 50003—2011《砌体结构设计规范》,水灰比(质量比)设计为0.6,配合比设计为m(砂):m(水泥)∶m(水)=1 680∶560∶336.试件尺寸为100 mm×100 mm×100 mm.先制成完整试件I1、I2.为了得到含预制裂纹的试件,在砂浆浇筑和振捣后,插入不同长度和角度的钢片,待砂浆凝固成型后取出.其中:编号L1~L6 表示试件中的裂纹长度为1~6 cm、间隔为1 cm;编号A1~A7 表示试件中的裂纹角度为0°~90°,间隔为15°.
3.2 试验方案
图1 中的有机玻璃楔块角度分别为52°和71°.为减少界面间超声波的能量损耗,楔块组、试件及超声波换能器间使用凡士林紧密粘接.试件底部两端通过平台固定.基频波频率比d为0.83,第1 列正弦波频率为48 kHz,第2 列正弦波频率为40 kHz.示波器采样率设为5 MS/s.针对2 组不同长度和不同角度预制裂纹的试件,分别运用非共线混频法和高次谐波法进行探测,对比和分析2 种非线性超声检测方法的优势和不足.
3.3 混频测试结果与分析
3.3.1 最佳幅值的选取
首先分析试验设置的最佳激励幅值.针对完整试件,使用6种信号幅值(50、80、100、120、150、180 V)进行非线性超声测试,并作归一化处理.信号幅值的设置间隔为两端疏中间密,且50 V 以下测试结果离散性大,不稳定,180 V 则是仪器双通道幅值设置的上限.为提高测试结果的可靠性,每个幅值的测试重复9 次并取标准差,结果如图5 所示.由图5 可见,信号幅值标准差先减小后增大,在100 V 时达到最小值,且数据波动也最小,可最大可能地避免偶然误差的出现,故采用100 V 信号幅值进行试验.

图5 不同幅值下的非线性系数标准差Fig.5 Standard deviation of the nonlinear coefficient varies with amplitude
3.3.2 裂纹长度变化
编号为L1~L6 的试件所对应的裂纹长度为1~6 cm,间隔1 cm.激励电压设置为100 V,激发频率分别定为40、48 kHz.在各个试件相应的频域图中读出混频振幅A3等相应的参数,代入公式(3)求得混频法非线性系数β,并作归一化处理,结果见图6、7.

图6 不同裂纹长度下的βFig.6 β varies with crack length

图7 不同裂纹长度下的混频振幅Fig.7 Amplitude of mixing frequency varies with crack length
由图6、7 可知,随着试件中的裂纹长度依次增大,混频法非线性系数β和混频振幅A3都具有逐渐增大的趋势,即呈现正相关规律.超声波表示介质中振动的传播,而振动传播过程中会出现波的衰减现象如吸收、频散、漫射等.正如非线性系数β反映的是试件损伤情况,当预制裂纹的长度逐渐增大时,即表示试件损伤增大,这符合相应的非线性系数增大的趋势.同时这也与前面理论公式中表示的混频法非线性系数与裂纹长度成正相关关系的结论一致.其中有个别点呈现出较大的离散性,原因在于,砂浆是多组分复合材料,水化作用产生的微孔隙和颗粒界面分布具有较强的随机性和离散性;另外,试验中使用的接触式平面换能器不可避免地存在耦合误差,建议在后续研究中使用空气换能器,以降低测试系统产生的误差.
3.3.3 裂纹角度变化
编号为A1~A7的试件所对应的裂纹角度为0°~90°,间隔15°.同样设置激发电压为100 V,激发频率分别定为40、48 kHz.由每个试件的频域图读出混频振幅A3等相应的参数,代入公式(3)求得混频法非线性系数β,并作归一化处理,结果见图8、9.
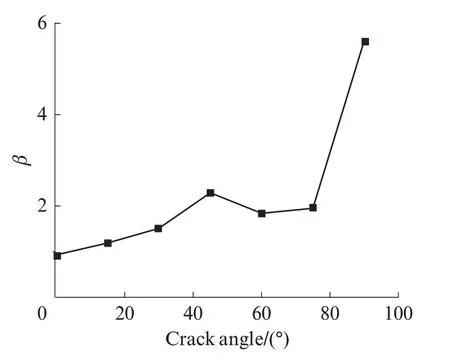
图8 不同裂纹角度下的βFig.8 β varies with crack angle
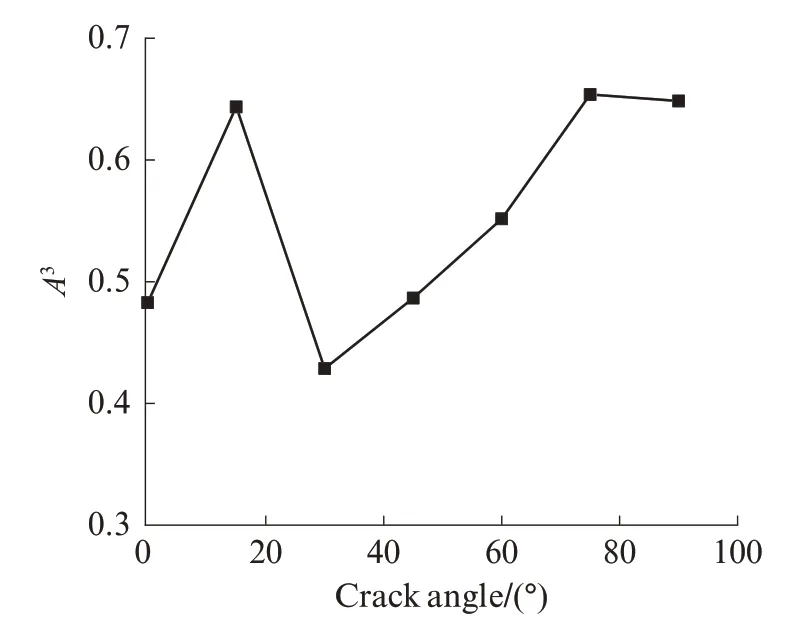
图9 不同裂纹角度下的混频振幅Fig.9 Amplitude of mixing frequency varies with crack angle
由图8、9 可见,随着试件中的裂纹角度依次增大,混频法非线性系数β和混频振幅A3同样呈现逐渐上升趋势,即β值随着裂纹平面与混频波传播方向夹角的不断增大而增大.裂纹角度逐渐增大,则混频波到达裂纹处产生的波的散射效应逐渐增强,由非线性系数表征的试件损伤效应增大.这也符合理论公式中混频法非线性系数与裂纹角度成正相关关系的结论[13].同样,由于试验仪器存在的耦合误差,其中有个别点呈现出较大的离散性.
3.4 非共线混频法和高次谐波法的对比结果
为了尽可能接近非共线混频法的试验条件,确保2 种方法的对比效果,高次谐波法采用正弦脉冲串波激发,激励频率为40 kHz,激励电压为100 V,采样率为5 MS/s.通过频域分析,分别得到基波、2 次、3次谐波振幅,代入相应的高次谐波非线性系数表达式并作归一化处理[15-16],得到2 次、3 次谐波的非线性系数β2、β3,结果见图10、11.由图10、11 可知,高次谐波法可能受到了系统非线性源干扰等因素的影响,所得到的β2、β3值随裂纹长度和角度变化的趋势不明显,不容易看出规律.相较而言,混频法非线性系数不管是与裂纹长度还是与裂纹角度都具有更明显的正相关关系.

图10 2 次谐波和非共线混频非线性系数对比Fig.10 Comparison of nonlinear coefficients of second harmonic and non-collinear mixing

图11 3 次谐波和非共线混频非线性系数对比Fig.11 Comparison of nonlinear coefficients of third harmonic and non-collinear mixing
在对比高次谐波和非共线混频试验结果时,采用敏感度系数、标准差和离散系数来表达各非线性系数对相应参数变化的敏感性,并去除误差较大点,结果见表2、3.表中括号内的数值表示的是非共线混频法对高次谐波法的优越性,敏感度系数则由求相邻增量间隔的系数最后取均值的方法求得,公式如下:

式中:SAF为敏感度系数;Δβ/β为非线性系数的变化率;ΔF/F为相对应的频率或者幅值变化.
由表2、3 可见,大致趋势上,在敏感度系数、标准差和离散系数方面,非共线混频法对高次谐波法具有明显优势,其非线性系数对裂纹长度变化和角度变化都更为敏感.
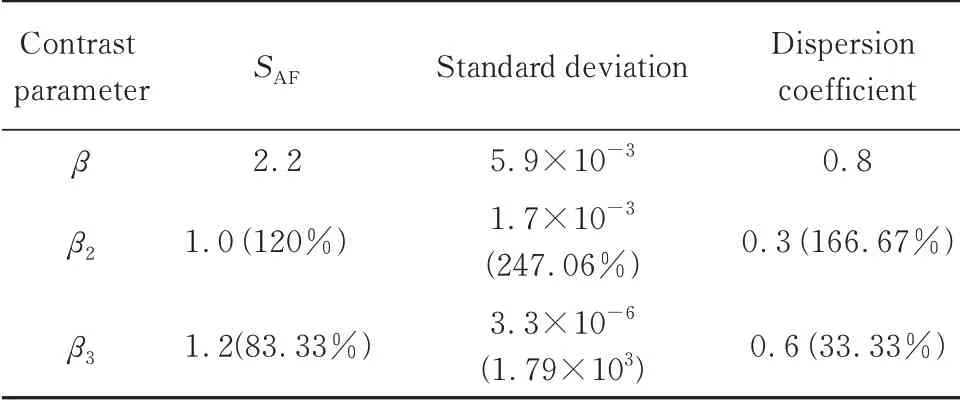
表2 不同裂纹长度下的非线性系数对比Table 2 Comparison of nonlinear coefficients in the change of crack length

表3 不同裂纹角度下的非线性系数对比Table 3 Comparison of nonlinear coefficients in the change of crack angle
4 结论
(1)以散射出混频波为依据,验证了非共线混频法的可行性.通过对比不同激励幅值所对应的试验结果可知,随着激励幅值的增大,混频法非线性系数标准差先减小后增大,因而确定了砂浆试件在当前条件下的混频最佳激励幅值为100 V.通过比较各幅值测试点的标准差,确认了混频最佳激励幅值,这可为其他材料测量提供依据.
(2)忽略离散性较大的数据点,随着裂纹长度和裂纹角度的增大,混频法非线性系数和混频振幅总体呈上升趋势,验证了混频法非线性系数与裂纹长度、裂纹角度成正相关关系的理论分析结果.
(3)利用敏感度系数、标准差和离散系数等参数,通过与高次谐波法试验结果对比可知,非共线混频法对裂纹长度和裂纹角度的变化更为敏感,表现的趋势更明显.
(4)试验过程中将产生换能器与试件表面之间黏结的耦合误差,试件表面的平整程度、气孔大小与数量等都会对试验结果造成影响.建议严格控制试件振捣、浇筑与成模过程中的施工质量,并采用空气换能器来降低耦合误差.

