机载中空纤维膜组件壳程气体流动数值模拟

刘国田，白文涛，潘江丽，陈广豪，潘俊，冯诗愚，*

（1.南京航空航天大学 航空学院 飞行器环境控制与生命保障重点实验室，南京 210016；2.中国航空工业集团有限公司 南京机电液压工程研究中心 航空机电系统综合航空科技重点实验室，南京 211106）

中空纤维膜具有单位体积装填密度高、占地面积小、分离效果好等特点，被广泛应用于气体分离、海水淡化、水处理及生物医学工程等方面。因氧气和氮气在膜丝上渗透速率存在差距，在膜丝内外气体分压力差的驱动下，氧氮可以实现分离，从而在膜丝两侧形成富氮和富氧气体。飞行器燃油箱机载惰化系统利用中空纤维膜组件产生富氮气体，并将富氮气体引入油箱中来降低油箱氧浓度，从而实现达到防火抑爆的目的［1-5］。

虽然通过试验方法来测量膜组件的性能是最为常见的方法，但是试验代价高，周期长。因此，近年来已经有大量采用数值计算方法来获取膜组件性能的研究。最为常见的研究是分析不同膜丝内侧操作参数和结构参数对分离性能的影响，如Ahmad［6］和Marcos［7］等采用数值方法研究了膜丝的浓差极化分布。Parvareh等［8］研究了压力对微滤膜渗透通量的影响。卞锐和许松林［9］利用数值模拟软件研究了入口速度和管径对中空纤维式渗透汽化膜内流动特征及分离性能的影响。Ardaneh等［10］建立二维数学模型研究了进口原料质量流量、压力及膜丝长度对气体分离效率的影响。这些研究中大多对膜丝外侧即壳侧进行了简化处理，认为壳程的流动差异不会影响分离过程。

显然，壳程中由于膜丝的分布可能存在不均匀等现象，壳程各处的浓度分布也会有差别，这将导致分离存在差异。显然，了解壳程的流动情况可以更加精确地预测膜组件的分离效果。杨毅等［11］利用随机顺序添加算法创建了膜组件的三维数学模型，研究了膜丝轴向的非平行分布对组件径向局部沟流和死区的影响。Buetehorn等［12］对不规则纤维排列组件单元进行了计算流体力学（CFD）方法模拟。吴云等［13］利用数值模拟的方法研究了不同填充方式下生物膜反应器内流场特性。Costello等［14］对不同排布方式的中空纤维膜组件进行了壳程流动阻力系数的实验测量，结果表明不均匀排布阻力系数明显小于均匀排布时的阻力系数。Cai等［15］模拟了中空纤维膜壳侧流动和组件整体传质特性。Ma等［16］模拟了膜纤维间距和位置对不同位置纤维的过滤性能的影响。这些研究表明，壳程中介质的流动和浓度分布差异不应当被忽略。

上述研究中均为液膜，目前国内外鲜有气体分离膜壳程流动分布的研究报道，其主要原因在于气体黏度小，流动阻力低。因此，壳程的不均匀性对民用气体膜组件分离影响较低。然而，机载膜组件所要求的尺寸小，操作强度大，填充密度高，加之随着飞行高度变化，壳程气体密度急剧降低，体积流量增加，因此迫切需要掌握壳程中气体的流动情况。鉴于此，采用CFD方法对燃油箱惰化用机载中空纤维膜组件壳程进行建模仿真，分析不同工况下的组件壳程气体流动分布情况。在相同条件下，膜丝束间距、膜丝束排布方式和飞行高度会影响气体在膜丝束间和组件内壁处流动量的比值，但膜丝束入口速度对比值影响较小，这些结论为机载膜组件设计和相关研究提供参考。

1 模型和计算

1.1 计算模型的建立

以某中空纤维膜组件为研究对象，几何结构参数如下：组件外径为300 mm，长度为690 mm，膜丝外径为0.16 mm，因填充密度不同，组件含有膜丝几万到十几万根，膜组件圆形出口半径为10 mm，圆心距离上端口60 mm。考虑建模的可行性和网格数量的经济性，在此实物基础上进行了如下模型简化：①组件中膜丝以千根膜丝捆扎成膜丝纤维束的形式存在，膜丝束半径R=3 mm；②膜丝束排布均匀，膜丝束间距L为相邻两束圆心距离减去两圆半径；③膜丝在轴向直线分布，不存在弯曲和变形。基于以上假设简化，在CATIA中建立简化模型，如图1所示。

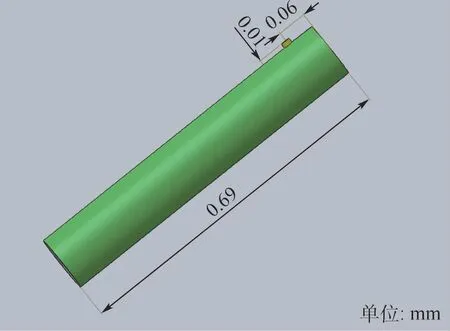
图1 膜组件几何模型Fig.1 Geometric model of membrane module

1.2 网格划分和模型求解

将CATIA模型导入ICEM CFD中进行非结构化体网格划分，模型采用八叉树方法生成四面体混合网格，在膜丝和出口处采用较为细致的网格结构，其三维非结构网格如图2所示。

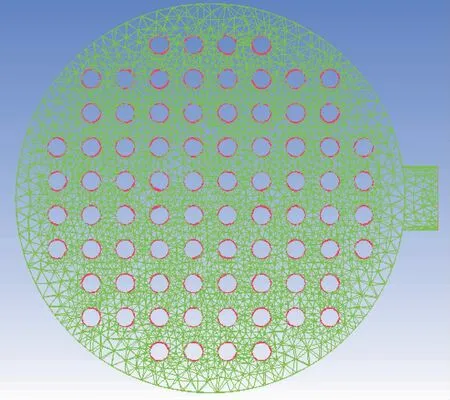
图2 膜组件三维非结构网格Fig.2 Unstructured 3D mesh of membrane module

采用定常稳态方法模拟中空纤维膜组件壳程气体流动状况。建立组件的几何模型和划分三维体网格后，用FLUENT求解流场的连续性方程和动量方程组：

式中：下标1、2分别为进口、出口参数；Vn为垂直于截面方向的速度；ρ为气体密度；A为截面面积；¯v为气体速度向量；f为质量力；pn为表面力。

在FLUENT中，将膜丝束外表面设为速度入口，组件出口边界类型为压力出口，组件外壁的边界类型为壁面。以二阶迎风格式离散方程，采用基于压力的绝对速度方程、标准k-ε湍流模型并利用SIMPLE算法求解流场。

1.3 网格无关性验证

为验证模型网格无关性，将模型分别划分为150万、400万、650万数量网格，以出口截面面积加权平均速度vout为检验标准，网格无关性验证结果如图3所示。由图3可知，网格数量对出口平均速度值影响不大。综合考虑计算的精度和效率，网格数量选取为400万。

图3 网格无关性验证Fig.3 Gird independence verification

2 工况条件和截面平均速度比定义

2.1 工况条件

借鉴文献［11-16］研究，膜组件壳程的流动影响因素有组件的膜丝束排布方式和填充个数、膜丝束入口速度、流量等。考虑所研究的膜组件用于机载惰化中，因而需要考虑飞行高度变化带来的环境压力的改变。因此，进行了不同工况下的几何建模和数值计算。

1）保持膜丝束入口速度不变，改变膜丝束间距L，随着膜丝束间距的改变，膜丝束填充数随之改变。当L分别为3.0R、2.5R、2.0R、1.5R、1.0R时，对应的膜丝束填充个数为32、52、60、80、112。

2）保持膜丝束入口质量流量不变，随着膜丝束间距的增大，出口速度增大。当L分别为3.0R、2.5R、2.0R、1.5R、1.0R时，对应的膜丝束入口速度为0.010 5、0.006 5、0.005 6、0.004 2、0.003 m/s。

3）保持膜丝束间距不变，更改膜丝束入口速度为0.003、0.005、0.007、0.009、0.011 m/s。

4）保持膜丝填充个数不变条件下，比较膜丝束均匀排布和不均匀排布流动，分析排布方式对流动特性的影响，如图4所示。其中不均匀排布是几何建模型时，手动划分填充同数量不相交膜丝束。

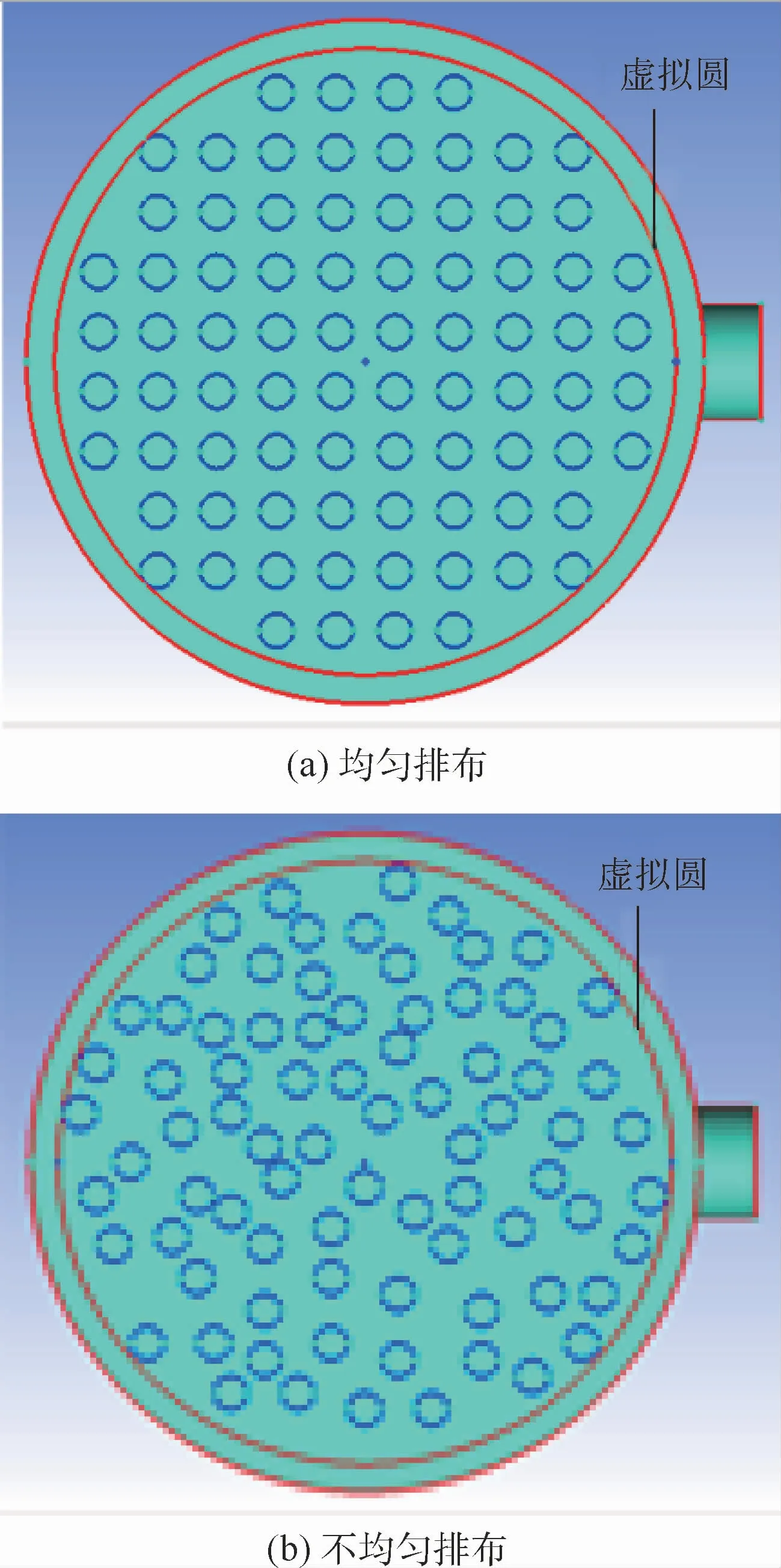
图4 膜丝束排布方式Fig.4 Arrangement mode of membrane tows

5）在保持膜丝入口速度为0.003 m/s、膜丝填充数量为80、膜丝均匀排布时，定义膜组件出口压力为环境背压，改变出口背压，模拟计算飞行高度为2 000、5 000、7 000 m时的工况。在对流层中，大气环境压力与高度的关系为

式中：ph为不同飞行高度上的压力，Pa；p0为海平面大气压力，p0=101 325 Pa；h为飞行高度，m；g为重力加速度，g=9.8 m/s2；α为年平均温度直降率，α=0.006 5℃/m；r为气体常数，r=287 J/（kg·K）。在飞行高度h为2 000、5 000、7 000 m时，对应的大气环境压力为79 504、54 001、41 078 Pa。

2.2 截面平均速度比定义

以轴向不同截面进行气体流场分析，在每一截面上以一个包围所有膜丝束的虚拟圆将截面分成内圆和圆环2个面，如图4所示，其中虚拟圆半径为55 mm，内圆为膜丝束间部分，圆环为组件内壁部分。并定义截面平均速度比θ（无量纲）来描述壳程气体流动分布情况，表示为

3 计算结果分析

膜丝束间距为1.5R，膜丝束表面速度设为0.003 m/s时，组件轴向截面速度v和压力p的云图如图5所示。由图5可以看出，速度和压力在出口处变化急剧，在组件内变化较小。组件内压力速度变化小是因为组件中气体流速慢，此外气体黏度小，流动阻力低，流动损失小；出口处速度压力变化剧烈是因为流动截面的急剧收缩。其他工况下速度、压力云图趋势与之相似。

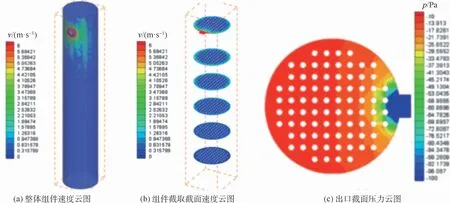
图5 膜组件速度和压力云图Fig.5 Velocity and pressure contour of membrane module

3.1 膜丝束间距对壳程气体流动分布的影响

入口速度不变，不同L下的θ值如图6所示。由图6可见，保持膜丝束入口速度为0.003 m/s时，截面平均速度比θ随着膜丝束间距的减小先减小后增大，在间距为1.5R时候达到最小值。

图6 入口速度不变时不同L下的θ值Fig.6 Values ofθfor different L with constant entrance velocity

在入口流量不变的情况下，不同L下的θ值如图7所示。由图7可知，与膜丝束入口速度不变下相似，在膜丝束保持入口质量流量为定值时，截面平均速度比θ随着膜丝束间距的减小先减小后增大，在间距为1.5R时候达到最小值。这是因为：在膜丝束间距较大时，膜丝束间的距离尺寸与组件内壁处缝隙尺寸相近，膜丝束间的轴向流动阻力与组件内壁处的轴向流动阻力量级相当，而随着膜丝束间距的缩小，膜丝束间的轴向流动阻力较大，气体克服膜丝束间径向阻力后会涌向内壁处流动，这一过程导致内壁处气体流动量增大，膜丝束间气体流量减小，从而使得θ值减小。而膜丝束间距进一步地减小会导致膜丝间的径向阻力增大，气体不能克服阻力向组件内壁处流动，从而导致膜丝束间的气体流动量增大，使得θ增大。

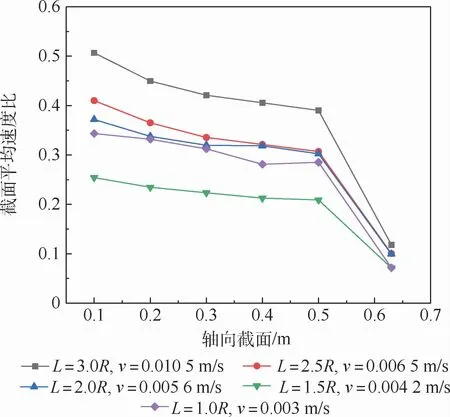
图7 入口流量不变时不同L下的θ值Fig.7 Values ofθfor different L with constant entrance flow rate

3.2 入口速度对壳程气体流动分布的影响

保持膜丝束间距不变，增大膜丝束入口速度，不同v下的θ值如图8所示。由图8可知，θ值随v变化不大。这是因为：入口速度微量级的改变，引起的雷诺数变化很小，产生的阻力变化也较小，壳程气体的流动也不会发生明显的变动。

图8 膜丝束间距不变时不同v下的θ值Fig.8 Values ofθfor different v with constant entrance L

3.3 膜丝束排布方式对壳程气体流动分布的影响

对膜丝束填充数为60、80的2个模型分别进行均匀排布和不均匀排布建模。不同膜丝束排布方式下的θ值如图9所示。由图9可见，与均匀排布相比，不均匀排布时的θ更大。这意味着均匀排布时膜丝束间流动的气体量更少，气体量少的原因是由于膜丝束间阻力大造成的，这与Costello等［14］的研究结果一致。Costello等［14］对不同排布方式的中空纤维膜组件进行了壳程流动阻力系数的实验测量，结果表明不均匀排布阻力系数明显小于均匀排布时的阻力系数，不均匀排布时，组件膜丝束间阻力更小，因为气体流量更大。

图9 不同膜丝束排布方式下的θ值Fig.9 Values ofθin different arrangement modes of membrane tow

3.4 飞行高度对壳程气体流动分布的影响

飞行高度与组件截面、膜丝束间截面平均速度关系如图10和图11所示。由图10和图11可见，随着飞行高度的增大，出口背压减小，组件膜丝束间截面气体平均流动速度基本保持不变，但是整个膜组件轴向截面平均速度在增大。因此，背压改变对组件内壁处的气体流动分布有着重要影响，对膜丝束间气体流动分布影响不大。

图10 飞行高度与组件截面平均速度关系Fig.10 Relation between flight height and average section velocity of membrane module

4 结 论

膜分离空气形成富氮气体来惰化燃油箱是目前经济高效的燃油箱惰化技术。采用CFD方法对某中空纤维膜组件壳程气体流动进行了数值模拟，得到了不同工况下的组件轴向各截面的气体流动分布，研究结果表明：

1）在膜丝束入口流动速度或膜组件入口流量一定时，截面平均速度比θ随着膜丝束间距的减小先减小后增大，在间距为1.5R时候达到最小值，此时壳体气体流动在组件内壁处流动达到最大量。这表明在膜组件设计和使用时，壳程气流布局与膜丝束间距存在最优设计和选择。

2）在膜丝束间距不变的情况下，增大膜丝束入口速度对θ值影响不大，因而在实际使用中为了得到更多惰气量，可以适当增大壳程流量。

3）相同膜丝束填充数量下，不均匀排布时的截面平均速度比θ值比均匀排布的值更大，意味着均匀排布方式更有利于气体的分离。

4）当飞行高度增大而出口背压减小时，膜组件轴向截面平均速度增大而膜丝束间截面平均速度变化不大，这表明背压改变对组件内壁处的气体流动分布有着重要影响，对膜丝束间气体流动分布影响不大。