脉冲射流对环量控制翼型气动性能的影响

雷玉昌，张登成，张艳华，苏光旭

（1.空军工程大学 研究生院，西安 710051； 2.空军工程大学 航空工程学院，西安 710038）

飞行器上的襟翼、副翼等活动舵面一般被用来改变机翼的弯度和周围的流场特性，进而改变机翼上的气动力和力矩。活动舵面对提高飞行器的升力、改善升阻比起到了重要作用，但是复杂的舵面机械系统导致飞行器结构复杂、质量增加，隐身性能变差。为解决复杂的高升力舵面机械系统存在的弊端，国内外陆续使用环量控制技术来解决这个矛盾［1］。环量控制技术的发展是备受关注的主动流动控制方式之一。这种流动控制是指在机翼钝后缘表面开缝，在后缘上喷射切向射流，利用Coanda效应（压力与离心力的平衡使射流沿着后缘曲面流动），射流与外流混合后绕曲面外形流动，使流线偏折，并增大绕流速度，增加气流绕翼型的环量。由库塔儒科夫升力定理可知翼型升力会增加［2-3］。风洞试验和数值仿真的结果表明，环量控制技术对圆形Coanda后缘稳定切向吹气具有明显的气动效益，对缩短飞行器的起飞着陆距离、提高机动性等提供了可能性［3-4］。尽管有诸多好处，但是这项技术并没有应用于实际飞行器上，因为后缘射流需要从发动机引气或设置额外供气装置，由此带来的发动机推力损失及经济效益制约了该技术的实际应用。而脉冲射流能够大幅度降低环量控制射流所需的质量流量，并减少引气量［5］。考虑到节省1%的商用喷气燃料就相当于节省100万美元的运营成本，脉冲射流能够带来可观的经济效益［6］。为此，脉冲射流对环量控制翼型气动性能的影响规律，在着重分析其大迎角下的实际应用价值中有重要的研究价值。

国内外对环量控制射流都进行了一定程度的研究。Yaros等［7］证明了环量控制可使机翼最大升力系数增大4倍。Jones等［8］也证明了采用环量控制的机翼可以获得与传统高升力系统相当甚至更高的升力，但随着升力增大，所需要的射流质量流量也迅速增大。Kanistras等［9］通过实验的方法研究了不同后缘曲率对气动特性的影响，结果表明后缘曲率对升力系数的影响较大，对阻力系数的影响并不明显。Jones等［10］提出了升力增长存在分离区和超环量控制区2个控制阶段，这取决于后缘形状和射流特性。AVT-239任务组［11］设计制作了利用环量控制技术替代传统舵面的无人飞行器，验证了该技术可用于改善升阻特性。朱自强和吴宗成［12］总结了之前环量控制技术研究的最新进展，并指出了国内对环量控制技术研究经验和成果的缺乏。张艳华等［13-14］研究了环量控制的作用机理，特别是对等离子体环量控制进行了深入研究，相较于普通射流环量的控制效费比较大。南京航空航天大学、西北工业大学等也进行了相关研究［15-17］。上述研究都集中指出了定常射流只能在较低迎角下带来巨大的升力效益，高动量系数导致失速迎角提前，并在大迎角下气动效益变差；同时，高动量系数需要消耗大量的质量流量，影响飞行器的推力效益。这些问题都严重制约了环量控制技术的进一步应用。

Jones和Englar［3，18］用 脉 冲 射 流 替 代 定 常 射流用以环量控制吹气，证明了脉冲射流能够在取得与定常射流相当的升力情况下，降低约50%的质量流量，初步证明了脉冲射流的部分优越性，但是并未解释射流作用机理，也未解决脉冲射流带来的气动力脉动问题。随后，Shah等［5］进一步分析了脉冲射流对后缘不同位置的速度影响，以及后缘射流分离点和边界层厚度的变化。王万波和Warsop等［19-20］也进行了相关研究，分析了0°迎角下不同频率时脉冲吹气对翼型气动性能的影响，同时指出仍需进行动量系数、占空比等因素的影响研究。已有的研究多关注脉冲射流作用下的时均气动力效应，对相应的气动力脉动现象和大迎角下的流动情况研究较少，难以指导实际应用。

为此，本文采用雷诺平均Navier-Stokes方法对二维环量控制翼型流场进行非定常数值模拟。对比研究脉冲射流和定常射流参数对翼型气动特性的影响，对大迎角下的流动情况进行分析，探究减弱气动力脉动现象的方法，为脉冲射流的具体应用提供一定的参考。

1 数值计算方法与验证

1.1 计算模型和网格

超临界翼型有钝前缘、大厚弦比的特点，最大升力系数较大，内部能够容纳环量控制技术所需要的供气机构或管道等，可以更充分地发挥环量控制增大升力的优势，因而成为环量控制技术研究的良好翼型。本文采用相对厚度为17%的超临界翼型NASA LS（1）-0417作为基准翼型。

翼型相对厚度为17%，弦长c=240 mm。采用文献［18］中的修形方法，将距后缘25%弦长的部分修形处理，按照后缘半径r/c=2%绘制柯恩达后缘曲面，射流口偏离中轴线15°，射流口高度h=0.001c。图1为修形过的超临界翼型示意图，研究仅涉及上射流口吹气。

图1 翼型相关参数示意图Fig.1 Sechematic map of airfoil shape parameters

计算区域选取翼型弦长的30倍，网格剖分采用结构网格，生成O型网格拓扑结构，边界层内第一层的网格高度约为1×10-5m，射流口附近第一层网格高度为2×10-6m，保证第一层高度的壁面率y+均小于1，以满足黏性底层的计算要求。网格总数约为58万，图2为翼型计算网格划分情况。

图2 翼型计算网格划分Fig.2 Airfoil’s computational grid generation

1.2 计算方法

数值模拟方法采用二维雷诺平均Navier-Stokes方程，积分表达式为

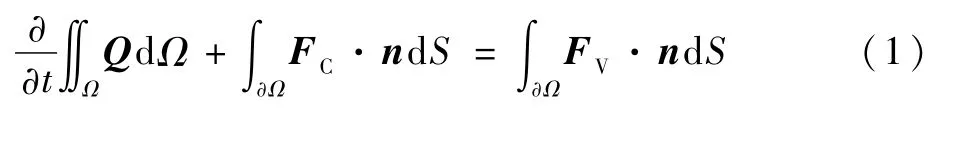
式中：Q为流动变量矩阵；Ω为控制体；S为控制体面积；FC和FV分别为无黏性通量和黏性通量；n为控制体面的外法线向量。采用k-w SST湍流模型，该模型对有较大逆压梯度的边界层流动、分离预测性能较好。Swanson等［21-22］也曾指出该模型能较好地预测环量控制流动分离。借助商业软件FLUENT进行相关计算，采用有限体积法离散控制方程，无黏性通量采用三阶MUSCL格式，黏性通量采用二阶迎风格式离散。远场边界为压力远场，壁面边界采用无滑移壁面条件。

早期研究表明，方波脉冲射流比传统的正弦脉冲射流效率更高［23］。因此，本节采用方波脉冲射流进行相关研究，其中脉冲射流在一个周期内对应的射流速度为

式中：T为脉冲周期；topen为一个脉冲周期中射流口产生射流的持续时间；DC为占空比；Vjet.max为在一个周期中射流产生的最大射流速度。射流动量系数为衡量射流强度、表征气流动量的重要无量纲参数，定义为

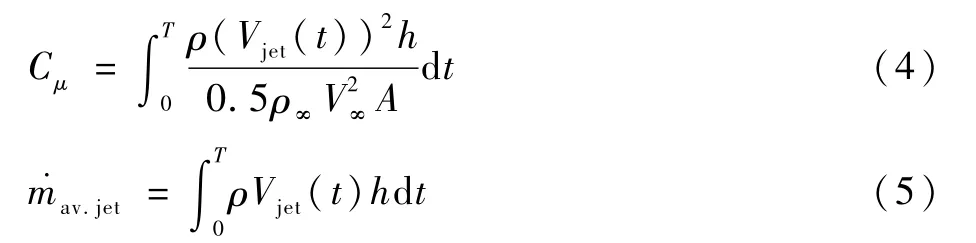
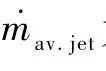
非定常计算中，物理时间步长对数值计算起着重要的作用。特别是对脉冲射流而言，出口速度随时间变化呈现出周期性变化，时间步长必须足够小以解析脉冲射流的周期性变化。虽然时间步长过小会严重影响计算效率，但是对结果没有太大影响。图3为不同时间步长Δt下时均升力系数CL和阻力系数CD的计算结果。当Δt≤5×10-5s时，时均升力系数CL的最大变化为0.9%，时均阻力系数CD的最大变化为2.1%，对高升力系统而言，存有一定计算误差是可以被接受的。因此，选定计算时间步长Δt=5×10-5s，足以解析每个脉冲射流的周期性变化。

图3 不同时间步长下的时均升阻力系数Fig.3 Time-averaged lift and drag coefficient at different time step sizes

1.3 计算方法验证

为了验证本文中数值计算方法的准确性，对0°迎角下不同吹气动量系数的超临界翼型进行了数值模拟。计算条件为：来流速度为30 m/s，来流温度为293.15 K，雷诺数为5×105，后续研究均采用此外流条件。设置动量系数在0～0.06之间变化，将仿真结果与文献［18］中的实验数据进行对比，仿真采用稳态方法，结果如图4所示，仿真结果与实验数据基本吻合。

图4 升力系数仿真与实验对比Fig.4 Comparison of lift coefficient between simulation and experiment

已有的环量控制脉冲射流实验中无高频率内容，因此选择文献［3］中35 Hz脉冲射流频率下不同占空比的情况进行对比。图5给出了35 Hz脉冲射流频率下的时均压力系数Cp分布。从图中可知，数值模拟得到的翼型上下表面的时均压力系数Cp与实验结果基本吻合。

图5 35 Hz脉冲射流下时均压力系数分布Fig.5 Time-averaged pressure coefficient distribution under 35 Hz pulsed jet

2 结果分析

2.1 占空比的影响

占空比是脉冲射流对翼型气动特性的重要影响参数，通过调节占空比，可以获得相应质量流量的变化。为了研究占空比对气动特性的影响，本节对35 Hz脉冲射流频率下不同占空比情况的翼型气动参数进行了数值模拟。

图6为脉冲射流和定常射流下的时均升力系数随质量流量变化的对比曲线。其中，脉冲射流曲线对应的质量流量是在定常射流动量系数下通过改变占空比实现的；定常射流动量系数Cμ=0.02，不同占空比DC对应的射流速度如表1所示。定常射流曲线对应的质量流量是通过改变射流速度实现的，动量系数Cμ从0变化至0.02。

图6 不同质量流量下的时均升力系数对比Fig.6 Comparison of lift coefficient at different mass flow rates

表1 不同占空比对应的射流速度Table 1 Jet velocity corresponding to different duty cycle

由图6可以看出，在产生相同时均升力系数的基础上，脉冲射流能够大幅度降低射流所需要的质量流量。在占空比变化阶段，脉冲射流作用下的气动性能差别较大，较低占空比作用下，脉冲射流降低质量流量的优势更加明显。在给定时均升力系数为1的情况下，脉冲射流对应的质量流量减少了68.4%，同时，在占空比为40%、质量流量相等的情况下，脉冲射流对应的时均升力系数相较定常射流提高了65.3%。随着占空比的增加，脉冲射流下的质量流量效益逐渐降低。

图7为不同占空比作用下的时均升力系数时域变化曲线。定义Δh为升力系数周期性变化过程中2个峰值之间的差值，即升力系数脉动幅值。占空比DC越小，升力系数脉动幅值Δh越大，这是因为低占空比对应的射流速度较大，是一种持续时间短、射流动量大的穿透状态，能在短时间内在后缘移动较大距离，而射流一旦消失，升力系数出现断崖式下降的现象，射流消失后的升力响应速度要远大于射流产生后的响应速度，同时，由于占空比较低，射流消失后逐渐逼近无射流状态下的升力系数。

图7 35 Hz脉冲射流下时均升力系数时域曲线对比Fig.7 Comparison of lift coefficient time-domain curves at 35 Hz pulsed jet

综上所述，在产生相同时均升力系数的前提下，脉冲射流需要的质量流量更小，且占空比越小，这种优势越明显。但是，低占空比下导致的射流穿透效应将会直接导致升力系数脉动幅值增大。当DC=30%时，Δh可达1.3，这在实际飞行中将会导致剧烈的抖振现象，严重影响飞行安全，在实际应用中是不可取的。因此，实际应用中应当选用较高占空比的脉冲射流，选取DC=70%进行后续研究，并进一步探索脉冲射流的实际应用前景及降低Δh的方法。

2.2 频率的影响

图8给出了在不同迎角α下频率的改变对升力系数增量ΔCL的影响。低迎角（0°）下，随频率增加，升力系数增量呈现先增加后降低的趋势，但整体变化幅度不大，在高频率（200 Hz）下，脉冲射流甚至低于定常射流作用下的升力系数增量；高迎角（15°）下，随频率增加，升力系数增量呈现持续增加的趋势，在高频率（200 Hz）下，脉冲射流远远高于定常射流作用下的升力系数增量。在不同迎角下，随频率增加，脉冲幅值Δh均逐渐减小，约在100 Hz逐渐稳定。综上所述，高频脉冲射流在较大迎角下有突出的应用优势，具备替代定常射流进行流动控制的潜力。

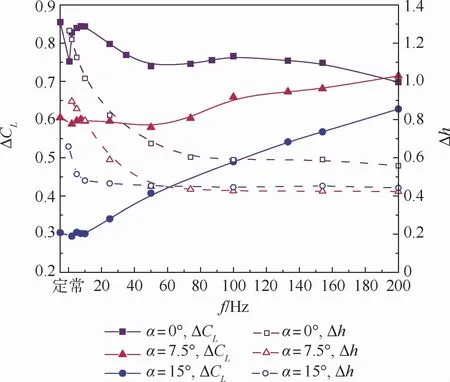
图8 不同频率下的升力系数增量和脉动幅值对比Fig.8 Comparison of lift coefficient and pulsation amplitude at different frequencies

为了分析脉冲射流作用下的流场作用机理，图9给出了迎角分别为0°和15°时200 Hz脉冲射流与对应定常射流作用下的翼型整体涡量图和后缘局部流线放大图。其中脉冲射流作用下各时刻对应的时均升力系数如图10所示，低频率下射流消失后时均升力系数不再呈现出断崖式下降的现象。

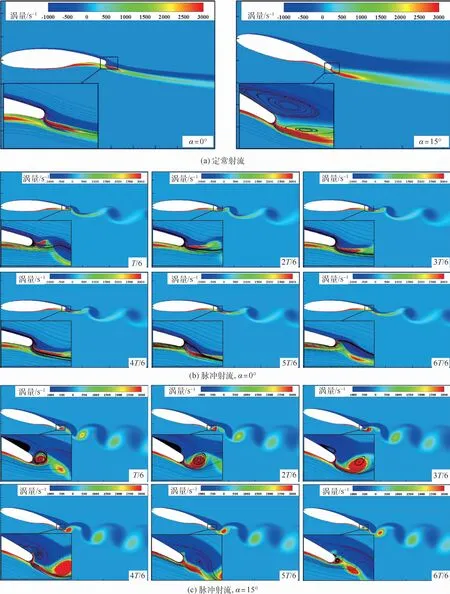
图9 翼型涡量图和流线图Fig.9 Airfoil vorticity and streamlines

以15°迎角为例进行分析，从定常射流作用下的翼型流线图中可以看出，翼型上表面已经出现大规模分离流动，涡流区较大，继续增大迎角会导致升力下降和阻力增加，翼型进入失速分离阶段。而脉冲射流作用下的翼型上表面分离涡与尾涡在一个脉冲周期内逐渐相互耦合，共同向后移动形成尾迹，上表面分离点明显后移，涡流区明显小于定常射流。而0°迎角下的翼型流线图，定常射流作用下的流动始终附体，并未出现分离流动，脉冲射流作用下的上表面涡量分布与定常射流作用下的涡量分布差别也并不明显。

从脉冲射流作用下的翼型流线图中可以看出，在T/6时刻，翼型上表面存在分离流动，并存在一个顺时针的分离涡，由于后缘射流的产生，后缘上方存在一个逆时针尾涡，同时，后缘射流下存在一组较小的附着涡，翼型处于临界失速状态。当进入2T/6时刻，随着后缘持续射流，后缘压力逐渐减小，后缘上方的逆时针尾涡先向后移动，此时上表面分离涡变化不大。当进入3T/6时刻，后缘压力继续减小，此时翼型上表面的分离涡也逐渐后移，分离涡几乎已经移动至翼型尾端，翼型已经远离失速状态，后缘涡进一步后移会导致升力系数下降，如图10中2T/4时刻所示。

图10 200 Hz脉冲射流下时均升力系数时域曲线对比Fig.10 Comparison of lift coefficient time-domain curves at 200 Hz pulsed jet

当进入4T/6时刻，原尾涡向后移动至消散，上表面分离涡逐渐呈现脱离状态，逐渐耦合形成新的尾涡。当进入5T/6时刻，射流已消失，此时分离涡已完全脱离，与原本位于射流下方的附着涡相互耦合，向后移动。尾涡逐渐被外流吹散，上表面流动逐渐恢复为附体。此时由于射流存在时滞效应，后缘压力并未迅速提高。当进入6T/6时刻，后缘无射流，此时流动状态趋向于15°迎角下的无射流定常状态，钝后缘形成新的一组附着涡，翼型上表面压力较低，附着涡逐渐上移形成上表面的大分离区。随后，后缘射流产生，射流上方产生新的尾涡，下方产生新的附着涡，流动开始向下一个周期发展。

总体来看，翼型上表面的分离涡和后缘尾涡在一个周期的演化过程中，经历了形成、后移、脱落、消失、再形成的过程。而高频脉冲射流在大迎角下的气动效益如此突出，是因为其不断促进翼型上表面的分离涡脱落。

与15°迎角相比，0°迎角定常射流作用的翼型上表面并未分离，流动始终附体。从整体流场来看，15°迎角上表面的分离涡不断被吹除，涡流区明显减小，较定常射流而言，升力增大；而0°迎角上表面不存在分离涡，尾迹受射流速度的影响跨度明显较长，较定常射流而言升力略有降低。

从后缘流场来看，在整个周期并未形成如同15°迎角下明显的分离涡与尾涡相互耦合向后移动的状态，更多表现为流线的上下偏折。这是因为0°迎角上表面涡强较弱，后缘难以耦合形成有效的涡旋。0°迎角下被不断吹除的尾涡强度较低，连续性也较弱，因此，0°迎角下脉冲射流受频率影响较低。

因此，对于低迎角而言，脉冲频率更多表现为对升力系数的直接影响，与定常射流的作用机理是一致的，其效果类似于间歇性施加射流；而对于高迎角而言，脉冲频率更多与分离涡移动、尾缘涡脱落频率等相关，这种流动状态已经与定常射流完全不同。特别是在整个流动周期中，分离涡的移动都远离失速状态，这一特性表明借助脉冲射流有望突破静态失速迎角这一禁区。

2.3 动量系数的影响

图11为不同动量系数下脉冲射流、定常射流、无射流及基准翼型NASA LS（1）-0417的升力系数对比曲线。基于上述对占空比的研究，选取脉冲射流占空比为70%，动量系数分别为0.02和0.04。从图11（a）可以看出，在动量系数为0.02的情况下，当迎角小于10°时，定常射流能够较大幅度地提高翼型升力系数，当迎角大于10°时，提升幅度逐渐降低，而且失速迎角提前。为了衡量动量系数带来的影响，引用效费比ΔCL/Cμ参数。0°迎角下，翼型效费比为42.6，此时翼型升力系数提高144.5%；而15°迎角下，翼型效费比降为15.2，此时翼型升力系数仅提高18.8%，同时，失速迎角由15°提前到10°。当迎角小于5°时，定常射流升力系数大于脉冲射流；当迎角大于5°时，定常射流升力系数小于脉冲射流。相较定常射流，脉冲射流能在更大的迎角范围内大幅度提高翼型升力系数，更加适合在大迎角下工作。在15°迎角时，ΔCL/Cμ=38.3，此时翼型升力系数仍能提高46.3%，同时，失速迎角大幅度延迟。

图11 升力系数对比Fig.11 Comparison of lift coefficient

从图11（b）可以看出，提高动量系数至0.04后，对于定常射流而言，在0°迎角下，ΔCL/Cμ=36.9，而在15°迎角下，翼型效费比降为11.9。随着动量系数的增加，定常射流的升力效益降低。定常射流对应的失速迎角也进一步提前，由15°提前至7.5°，同时，脉冲射流升力系数大于定常射流的转折迎角提前至2.5°。此时相较定常射流，脉冲射流在大迎角下有更突出的升力表现，在15°迎角下，ΔCL/Cμ=36.7。随着动量系数的增加，定常射流下的失速迎角会进一步提前，严重制约定常射流的升力效益。而脉冲射流大大扩宽了飞行器的可用迎角，甚至超过了无射流状态下的失速迎角，随动量系数增大，这种优势变得更加突出，完全弥补了定常射流在大迎角下存在的缺陷和不足。

从无射流状态和基准翼型NASA LS（1）-0417的升力系数对比中可以看出，修形后的环量控制翼型在无射流状态下升力系数比NASA LS（1）-0417高，添加射流后升力系数进一步提高。

为了更加全面地衡量脉冲射流、定常射流、无射流和基准翼型4种状态下的气动效益，并合理考量射流产生所需的能量消耗，参考文献［24］，假设射流是通过安装在机翼内部的气压泵实现的，气压泵吸入外界自由流动的气体后，经过压缩送入喷射槽形成射流。因此，能量消耗功率可由质量流量和总焓变化表示：

式中：Pc，jet为射流产生的能量消耗功率系数；Pt2和Tt2分别为自由来流的总压和总温；Pt1为射流出口处的总压；η为气压泵的工作效率，本节取0.85。脉冲射流采用振荡吹气执行器，即通过交替打开和关闭气压泵与喷射槽之间的连接，或打开和关闭气压泵与流体吸入通道之间的连接，通过调节阀门开度能够实现稳定或振荡射流。

为综合分析气动特性和能量消耗特性对射流控制效果的影响，采用Seifert［6］提出的气动品质因子AFM1进行衡量。该指标以升阻比为衡量基准，将射流功率转换为等效阻力，该值越大，则表明为执行器提供功率比为动力装置提供功率更有效，在增升减阻方面更有利，并表征射流控制效率越高。气动品质因子AFM1定义为

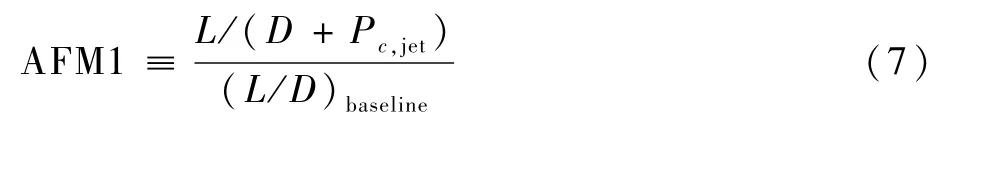
式中：（L/D）baseline为环量控制翼型无射流状态下的升阻比。

图12为不同情况下的AFM1对比曲线。环量控制翼型较基准翼型NASA LS（1）-0417而言，升阻比较低，这表明修形后的环量控制翼型尽管升力系数较大，但对应的阻力系数增长更为明显，导致升阻比降低，特别是在大迎角下降低明显。

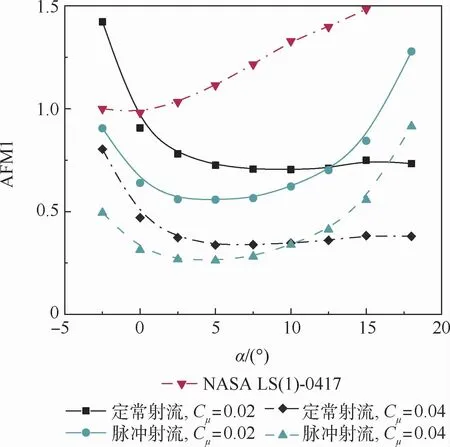
图12 气动品质因子对比曲线Fig.12 Aerodynamic quality factor comparison

对定常射流而言，随迎角增大，控制效率逐渐降低，然后基本保持不变。对脉冲射流而言，随迎角增大，控制效率先降低，然后迅速提高，逐渐超越定常射流。这是因为在中低迎角下，定常射流提升升力作用明显，而耗能低于脉冲射流，控制效率较高；随迎角增大，定常射流对升力的影响逐渐减弱，同时，翼型提前进入失速状态，控制效率降低。而脉冲射流在大迎角下升力系数提升明显，失速迎角推迟，控制效率逐渐增高。在考虑了射流消耗的情况下，脉冲射流仍能够部分改善环量控制翼型在大迎角下的气动效益，这与上文的研究是一致的。

2.4 叠加效应的影响

上述研究已经证明了脉冲射流在大迎角下卓越的性能优势，解决了定常射流在高动量系数、大迎角下升力增益较差的问题。但是由脉冲射流所带来的升力系数脉动现象仍未完全解决，本节提出采用脉冲射流与定常射流相叠加的方式来降低脉冲射流的升力脉动现象。维持其他参数不变，其中脉冲射流频率为200 Hz，DC=70%，Cμ=0.04。

定义定常射流部分与脉冲射流部分的比例为占比rsp，即rsp=Vjet.min/Vjet.max。叠加效应即研究占比rsp对气动特性的影响。图13为在15°迎角下，定常射流部分与脉冲射流部分不同占比rsp对应下的时均升力系数和脉动幅值变化趋势。随rsp的增加，时均升力系数逐渐下降，并且呈现先慢后快的下降速度。这表明适当添加定常射流并不会大幅度降低时均升力系数，同时能够有效降低单一脉冲射流时的升力系数脉动幅值。当rsp为0.84时，时均升力系数仅降低约12%，升力系数脉动幅值降低约80%，此时升力系数脉动幅值约占时均升力系数的3.7%，已经远远低于正常状态下大迎角下升力系数的脉动幅值［25］，能够满足飞行器在大迎角下的气动力要求。当rsp约为0.8时，有效解决了脉冲射流带来的气动力脉动问题，扩宽了环量控制技术的可用迎角范围。

图13 不同r sp下的时均升力系数与脉动幅值对比曲线Fig.13 Comparison of lift coefficient and pulsation amplitude at different rsp

图14给出了rsp分别为0.566和0.84时的后缘流线变化图。从整体上来看，后缘流场中的脱体涡都经历了生成、后移、脱落的过程。当rsp=0.566时，定常射流占比较低，定常射流速度较小，无法突破后缘外侧流动到后缘下方，当产生高速的脉冲射流后，射流需要从翼型后缘上方移动到后缘下方，导致升力系数脉动程度剧烈；当rsp=0.84时，从整体上来看，后缘流场中的脱体涡移动并不明显，此时定常射流占比较高，定常射流速度较大，已经突破后缘外侧流动到了后缘下方，此时在整个射流阶段，射流一直在翼型后缘下方进行移动，升力系数脉动减弱，同时，能够较大程度地保留脉冲射流不断促进翼型上表面的分离涡脱落特性，因此升力系数的下降并不明显。

3 结 论

本文采用非定常数值模拟方法，对脉冲射流作用下的环量控制翼型进行了相应研究，特别是分析了脉冲射流的实际应用前景，得到以下结论：

1）维持动量系数不变的情况下，较定常射流而言，占空比越低，脉冲射流减小质量流量的优势越明显，但同时升力系数脉动的劣势也越明显。

2）在占空比不变的情况下，小迎角下升力系数随脉冲频率增加而呈现先增加后降低的趋势，但整体变化幅度不大；大迎角下升力系数随脉冲频率增加而持续增加，高频脉冲射流在大迎角下有突出的应用优势。

3）脉冲射流作用下，翼型上表面的分离涡和后缘尾涡通过形成、后移、脱落、消失、再形成的过程，延迟了翼型失速，改善了翼型在大迎角下的气动特性，并且随动量系数的增大，这种优势更加明显。

4）采用脉冲射流和定常射流相叠加的方式能有效减弱升力系数脉动幅值过大的问题，当rsp约为0.8时，能有效扩宽环量控制技术的使用迎角。