捆绑火箭气动载荷分布不确定性分析
董欣心,刘莉,葛佳昊,王志
(北京理工大学 宇航学院,北京 100081)
火箭飞行过程中承受静态作用力和动态作用力,前者产生静载荷,后者产生动载荷。静载荷主要包括气动载荷、发动机产生的控制力、液体推进剂产生的晃动力等;动载荷主要包括阵风载荷、抖振载荷等[1]。火箭气动学科是总体设计的重要专业之一,气动特性分析得到的各项气动系数是载荷、姿态控制、结构设计等学科的先决条件,在火箭小回路设计中起到重要作用。然而在火箭飞行过程中包含许多不确定性因素,这种不确定性因素既有来自模型本身的不确定性,如在生产前无法完全准确获知结构尺寸及机械强度[2],也有由于对载荷条件知识缺乏造成的来自自然界的不确定性,如外界风场对于载荷的影响。准确的载荷分析是火箭结构设计的先决条件,优良的设计应能保证在任何外载荷的激励下都能可靠完成任务,因此,需对载荷的不确定性展开分析。
传统的火箭设计过程中,对于不确定性因素常采用计入安全系数的方式进行考虑,这种方式的问题在于安全系数的选取对于设计人员经验的依赖性较强,由于缺乏对不确定性的量化,安全系数过小无法保证安全,而过保守主义又会提升零件生产的经济成本,并且会带来不必要的质量增加。
近年来,不确定性优化设计[3-4]的概念逐渐在设计领域受到重视,其前提是不确定性量化(uncertainty quantification),主要思想是在设计过程中通过对模型输出响应的不确定性定量描述提升模型的可信度。不确定性分析可以帮助设计人员更好地量化模型响应的不确定性,获知模型置信度。对于气动载荷的不确定性分析主要集中在对气动力系数的分析,包括升力系数、阻力系数及俯仰力矩系数,可以据此计算机体或箭体所受的气动合力,为姿态控制专业提供上游数据。宋鑫等[5]对对称翼型开展了不确定性分析,得到了翼型气动性能定量变化区间,并以阻力系数最小为目标对其开展鲁棒性优化设计。针对由马赫数及迎角不确定性导致的气动性能波动问题,邬晓敬等[6]以NACA0012翼型为例,分析了跨声速阶段该现象产生的机理。
然而,仅关注气动力系数难以为火箭结构设计提供有效的指导,在结构设计过程中,需给出箭体分站上每一截面的内力,以便对火箭各部段分别进行设计。尤其是对于捆绑火箭,芯级与助推器捆绑处存在复杂的气动干扰问题。国内外学者对此类干扰问题开展了相关研究。Uematsu等[7]开展了高超声速流动条件下助推器与芯级分离的风洞试验,分别分析了不同攻角下不同截面形状的助推器在分离过程中对芯级的干扰冲击波形式。沈丹等[8]采用数值仿真模拟了高超声速条件下助推器头部对芯级的激波干扰,并对比了直头助推与斜头助推的干扰特性。由于捆绑火箭气动特性存在的复杂性及不确定性,了解火箭自身参数及大气条件等因素对气动载荷分布不确定性的影响是十分必要的。
不确定性分析方法主要可以分为概率方法[9-11](probabilistic methods)和可能性方法[12-13](possibilistic methods)。传统的概率方法多采用统计方法,如蒙特卡罗方法,其问题是所需样本数量较大、计算量较大及计算效率低,尤其是对于气动分析问题,单次计算花费时间较长,计算成本难以接受。广义多项式混沌方法(general polynomial chaos,gPC)作为一种非统计的概率方法,具有所需样本点数目少和计算精度高的优点,在气动分析领域得到广泛应用。Bettis等[14]依据配点非侵入式多项式混沌方法获取随机响应面,对运载火箭多学科分析获得的输出参数混合不确定性进行分析。Hosder等[15]采用稀疏的非侵入式多项式混沌方法及全局非线性灵敏度分析方法,对返回舱后体再入过程的辐射加热现象进行分析。宋赋强等[16]采用稀疏的非侵入式多项式混沌方法量化了乘波体的气动特性不确定性。
如果能够获知各项因素对响应不确定性的贡献程度,分析不确定性的主要来源,就能通过控制这些因素提升模型的置信度,此时需要引入灵敏度分析[17]。同时,由于不确定性分析方法的计算量会随输入参数的增加而大幅提升,合理选定输入参数非常重要,而灵敏度分析也为不确定分析中参数的选取提供依据。
首先,提出了依据多项式混沌理论,对捆绑火箭气动载荷分布开展全局灵敏度分析及不确定性分析的方法。然后,采用文献中给出气动特性实验数据的两捆绑火箭模型进行CFD分析,验证流场求解结果,并以此模型为基础建立外形参数化模型,对提出的方法进行验证。在来流参数及外形参数存在扰动的情况下,采用拉丁超立方采样获取样本点,通过CFD仿真分析获取样本点压力系数及黏性应力系数,分段积分得到气动力系数沿箭体分布,并由此计算气动载荷分布。最后,依据计算结果分析了流场的流动情况及气动载荷波动的产生原因。
1 气动载荷分布不确定性分析方法
1.1 灵敏度分析方法
常用的全局灵敏度分析方法有基本效应法[18]、基于导数的灵敏度分析法[19]、基于方差的灵敏度分析法[20-21]、矩独立灵敏度分析法[22]等,其中方差灵敏度分析法又称为Sobol方法,通过输入变量的方差在系统响应方差中的贡献度来衡量该变量的重要程度,能充分表征变量对响应的影响程度,因此,本文采用Sobol方法分析各因素对气动载荷的灵敏度。
将模型的不确定性输入定义为X,不确定性响应定义为Y,则该不确定模型函数可表示为Y=f(X),其中X=(X1,X2,…,Xn),为不失一般性,对各不确定性输入进行归一化处理,使n维输入变量在[ 0,1]内服从均匀分布,变量间相互独立,通过高维模型展开可以得到
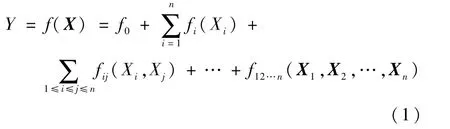
可以进行展开的条件为
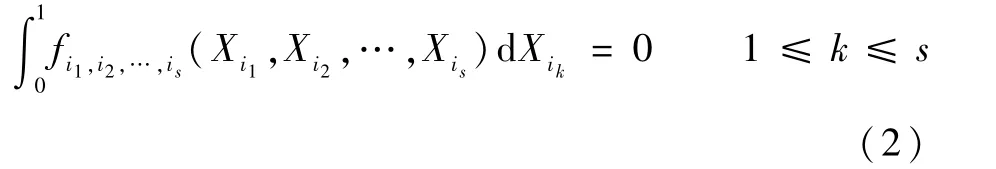
说明展开式中的所有项均两两正交,其表示为


对式(1)两侧同时取方差,得到
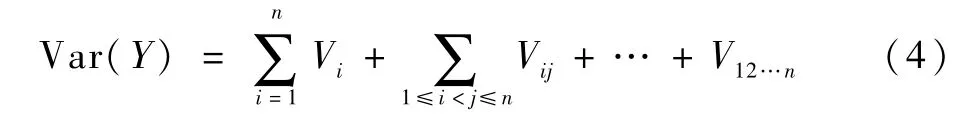
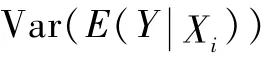
Sobol指数为[21]

Sobol指数的取值在[0,1]之间,且取值越大说明该输入变量对响应的影响越大。
1.2 不确定性量化方法
采用多项式混沌展开方法对系统进行不确定性分析,其思想在于将一个随机过程利用属于某特定分布类型的正交多项式混沌之和替代。假设有随机过程如下:

式中:ξ=[ξ1,ξ2,…,ξn]为服从一定分布的随机变量,并且相互独立。
则可将式(6)展开,并在有限阶截断得到
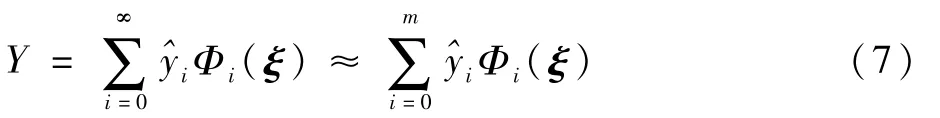

其中:n为随机变量数量;s为混沌多项式阶数。
依据Askey准则,正交多项式基底的选择取决于标准随机变量ξ的分布,自然界中大部分随机现象可以用高斯分布来描述,本文问题中讨论的不确定性变量也服从高斯分布,其对应的多项式为Hermite多项式。n维Hermite多项式表达式为
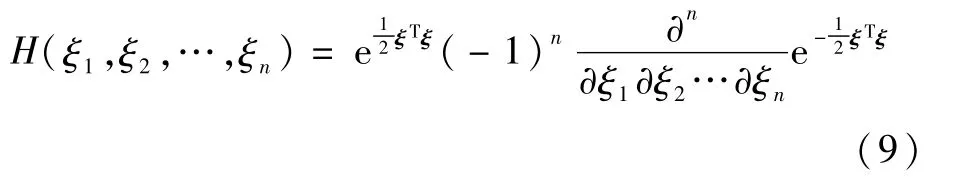

根据多项式混沌理论,得到原不确定性系统的前二阶统计矩为

1.3 载荷计算方法及仿真流程
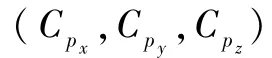
表妹和表妹夫这次彻底把心结打开,两人有所反思,他们约定为了共同的未来一起努力付出。经过调解他们的婚姻危机,乔振宇似有所悟,他不再跟我阴阳怪气地对话,份内的家务活也重新上手了。我们俩回到了以前的生活轨道上,可我觉得仅仅这样是不够的,这样只能让我们暂时回到貌似风平浪静的婚姻状态,可是,他的大男子主义不连根拔出,一旦出现新问题,我们的关系势必回到抱怨争执的状态,继续彼此伤害继续恶化,到那时候任凭多厚的爱情基础也扛不住这“强拆”啊!
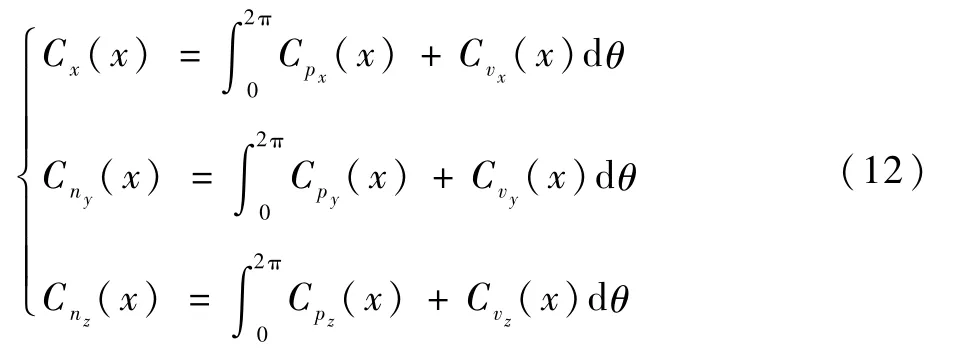
在实际计算过程中,对式(12)沿轴向按气动分站进行分段积分,得到每一站点的气动力系数,近似代替该段的气动力系数。由此结果可进一步计算得到沿箭体x轴分布的轴力及法向力为

仿真计算流程如图1所示,主要步骤如下:
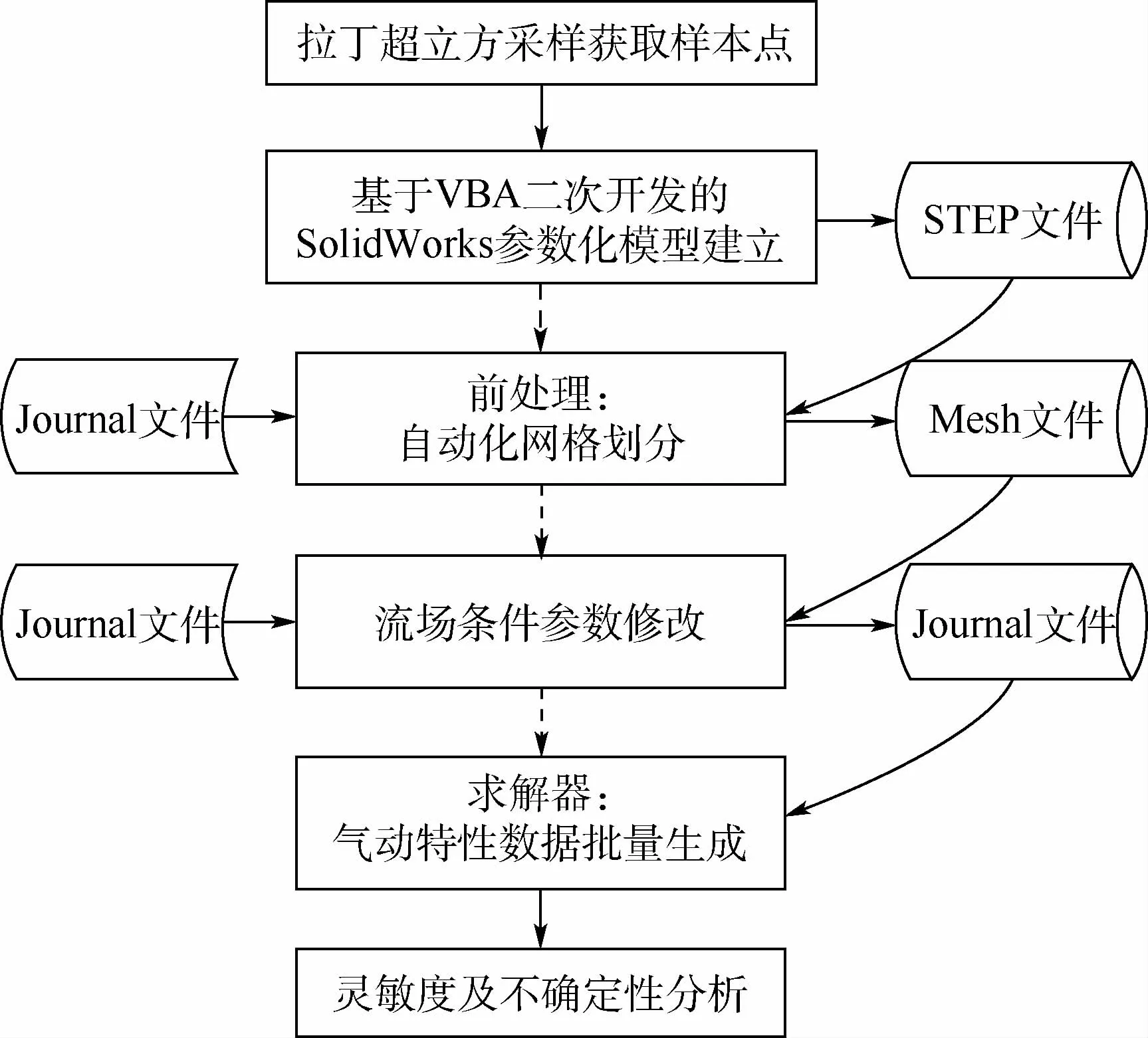
图1 仿真分析流程Fig.1 Flowchart of simulation and analysis
步骤1 依据多项式混沌展开阶数确定采样数量N,依据变量分布,采用拉丁超立方采样获得自变量X的N组样本点。
步骤2 基于VBA语言对SolidWorks二次开发,实现参数化模型自动更新,完成对结构外形参数的更新,导出STEP格式文件。
步骤3 采用CFD前处理软件Gambit对模型进行气动网格划分及边界条件设置,依据预先录制的Journal文件读取步骤2生成的STEP格式模型文件,进行自动化网格划分,并生成网格Mesh文件。
步骤4 依据预先录制的Journal文件实现CFD仿真条件设置,读取步骤3生成的Mesh文件,采用MATLAB脚本更改Journal文件,实现来流参数的自动更新。
步骤6 对求得的气动特性数据开展Sobol灵敏度分析及不确定性分析。
2 模型建立及流场求解
2.1 捆绑火箭模型参数化
为验证仿真分析结果的可靠性,以文献[23]中提出的两捆绑构型火箭模型为对象开展气动载荷不确定性分析,其外形如图2所示,具体参数数值在表1中给出。该模型平均了现有主要带捆绑运载火箭的外形尺寸参数,且文献中给出了该模型芯级表面压力系数分布的风洞试验数据。采用SolidWorks建模,并通过Excel中的VBA程序进行二次开发,可以实现外形自动化更新。
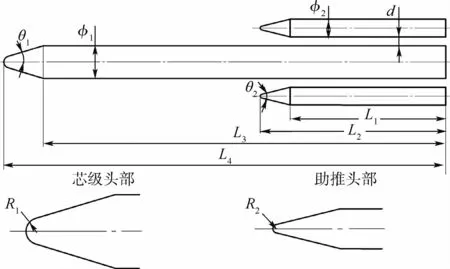
图2 捆绑火箭参数化模型Fig.2 Strap-on launch vehicle parametric model

表1 外形参数数值Table 1 Values of shape parameters
2.2 网格划分及流场条件设置
由于捆绑式运载火箭的外形较复杂,芯级和助推器之间存在小的间隙,难以采用结构网格来生成计算域的网格,模型气动网格生成采用非结构网格、圆柱形的计算域。首先,生成火箭壁面和圆柱面边界上的网格点,连接生成三角形网格。然后,采用阵面推进法生成四面体非结构网格。
为了获取更准确的计算结果,在火箭头部整流罩处和芯级与助推器间易产生气流干扰处进行局部气动网格加密。计算域的选择应保证流动能够充分发展,计算域选定为抛物面围成区域,长为90 m,底面半径为25 m,箭体头部距抛物面头部10 m。为降低计算量,用对称面将模型分为2部分,仅对半模型进行分析计算。最终生成四面体网格数量为793 678,箭体、计算域表面网格及边界条件设置如图3所示。

图3 网格划分示意图Fig.3 Schematic diagram of grid generation
模型验证工况及分析工况的流动条件均为高度可压缩流动,对于此类三维定常可压缩流动问题,选用密度基求解器能够获得更好的求解效果。采用基于节点的Green-Gauss函数求梯度,该方法精度较高,适用于非结构化网格。假设空气为理想气体,服从理想气体状态方程。湍流模型采用Spalart-Allmaras模型,适用于具有壁面限制的流动问题,对有逆压梯度的边界层问题能够求得较好的结果。
2.3 气动特性模型验证
为验证网格划分合理性与计算模型准确性,将仿真计算结果与文献[23]中提供的风洞试验数据进行对比。选用2种工况对计算结果进行准确性验证。其中,工况1为Ma=0.6、α=0°,工况2为Ma=2.0、α=0°。两助推中心轴线位于XOY平面内,假设迎角仅位于XOZ平面内(见图4),则法向力沿z轴方向分布。
就火箭芯级靠近助推器一侧,即图4中红色虚线所示位置的表面压力系数Cp沿箭体轴向分布。图5给出了本文及文献[23]的CFD仿真结果与风洞试验结果对比。从图5可以看出,本文的仿真结果与风洞试验数据吻合较好,略优于文献[23]的仿真结果,可以满足后续分析对模型精度的需求。

图4 迎角方向及表面压力系数提取位置Fig.4 Attack angle direction and surface pressure coefficient extraction location
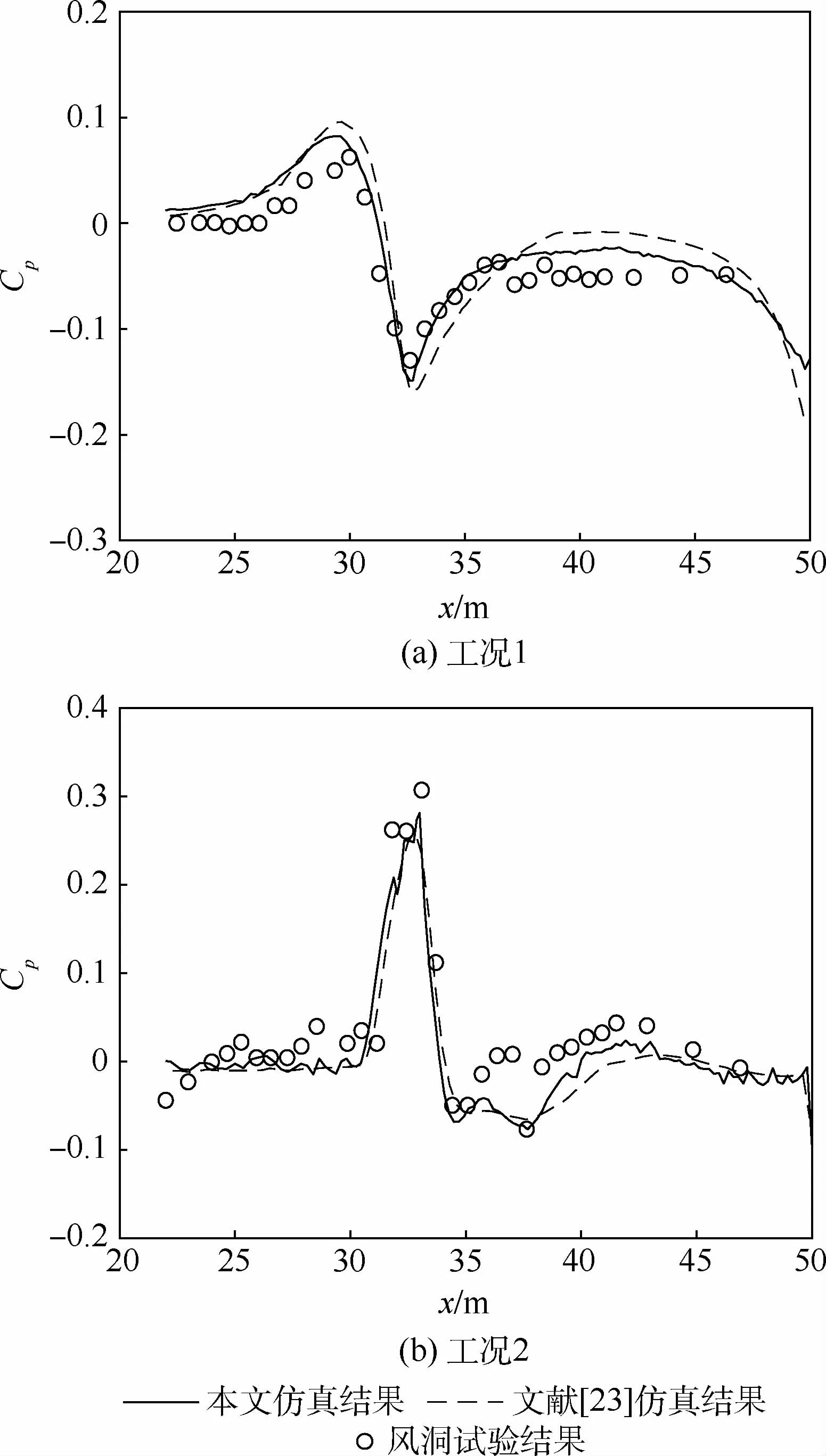
图5 表面压力系数分布对比Fig.5 Comparison of surface pressure coefficient distribution
3 仿真验证及结果分析
3.1 仿真参数设置
分析计算发现,气动载荷变化较为剧烈的主要为火箭头部整流罩处及捆绑与芯级发生气流干扰处,故将不确定性输入选为X=[θ1,d,Ma,α],包括2个几何外形尺寸参数,分别为整流罩头锥半顶角θ1和芯级助推间距d,以及2个气动参数,分别为飞行马赫数Ma和迎角α。分析上述参数在小范围内扰动对捆绑火箭气动载荷的影响情况。
自然界中的变量广泛服从正态分布,依据中心极限定理,误差可以看作是许多量的叠加,理应服从正态分布,因此,认为选取的变量均服从正态分布。选取火箭气动载荷分析过程中较为关注的最大动压状态进行分析,通过查阅相关型号弹道数据确定该工况对应的飞行状态。假设Ma均值为1.3,95%概率位于[1.2,1.4],即Ma~N(1.3,0.052);α均值为5°,95%概率位于[4°,6°],即α~N(5,0.52);θ1均值为17°,d均值为1 000 mm,均取变异系数cv为0.06,即θ1~N(17,1.022),d~N(1 000,602)。计算采用三阶多项式混沌方法,依据式(8)可得三阶四维问题的展开式项数为34,采样点数通常取项数的1.5~3倍[6],选取采样点为60。依据变量分布,采用拉丁超立方采样获得Ma、α、θ1、d的60组样本点。
3.2 灵敏度及不确定性结果分析
在结构设计过程中,通常采用分段设计方法,选取各部段载荷最大的截面,将最大载荷作为该部段的设计载荷,因此重点关注载荷峰值。气动载荷按沿箭体x轴方向及垂直于箭体x轴方向可以分为轴向力和法向力,依据式(13)计算得到各组样本对应轴向力及法向力分布。
依据载荷分布结果,分别选定轴向力分布在头锥处的峰值(峰值1)、法向力在头锥处的峰值(峰值2)及芯级和助推发生气流干扰处的峰值(峰值3)大小作为响应值,峰值所在位置如图6(a)、图6(b)中所示,分析头锥半顶角、芯级助推间距、迎角及马赫数对响应的灵敏度。分析得到Sobol指数如图7所示。
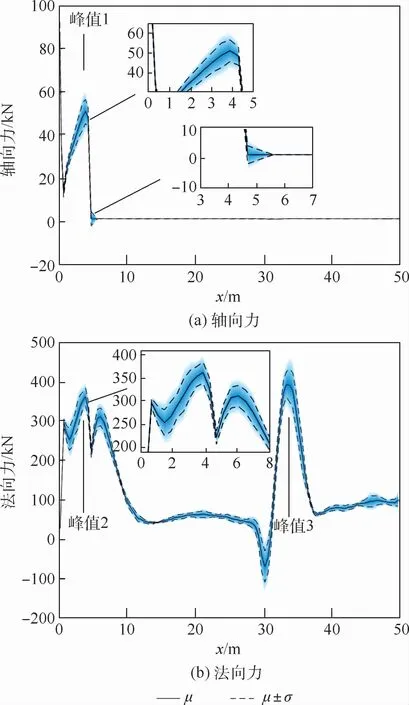
图6 轴向x及法向力不确定性分布Fig.6 Uncertainty distribution of axial force and normal force

图7 不确定性因素Sobol灵敏度指数Fig.7 Sobol sensitivity indices of uncertainty factors
从灵敏度分析结果可以看出,飞行马赫数对轴向力峰值的影响较大,而飞行迎角对法向力峰值有明显影响,对轴向力峰值影响很小。头锥半顶角对头锥处轴向力影响较大,而对法向力影响偏小;芯级助推间距对二者发生气动干扰处的法向力有一定影响,但其影响小于迎角及马赫数。马赫数对轴向力及法向力的作用包括力系数和动压2个部分,因此,对各响应值均有较大影响。
依据多项式混沌展开方法对轴向力和法向力分布的期望和方差进行分析,得到其不确定性分布如图7所示。图中:实线表示轴向力和法向力分布的期望值μ,即平均水平;虚线表示偏离均值一倍标准差位置μ+σ,即对应发生概率为65.26%;蓝色边界表示偏离均值二倍标准差位置μ+2σ,即对应发生概率为95.44%,颜色越浅表示载荷到达该值的概率越低。所关注载荷峰值出现位置、对应的均值、标准差和不确定度结果如表2所示。
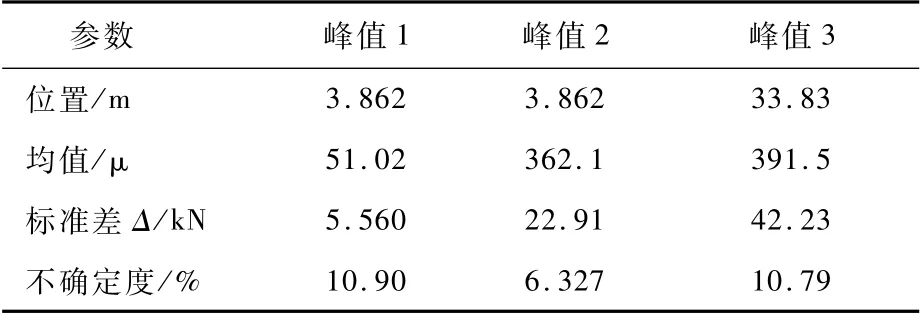
表2 不确定性分析结果Table 2 Uncertainty analysis results
从不确定性分析结果可以看出,轴向力的不确定性主要出现在头锥处,峰值1处不确定度为10.90%,其后在火箭芯级截面无变化处几乎为零,变化十分平缓,仅在出现助推器位置有微弱波动;相比之下法向力的不确定性较为显著,在头锥处、助推干扰处及尾段均有明显波动,峰值2处不确定度为6.327%,峰值3处不确定度为10.79%,在芯级截面不变且未与助推器产生气流干扰处同样存在一定的不确定性,主要是由于来流参数波动产生的。
3.3 流场结果分析
为了更直观地分析火箭几何外形对气动特性产生影响的原因,将迎角及马赫数固定为Ma=1.3,α=5°,分别分析d=1 000 mm时θ1=16°、θ1=17°、θ1=18°三 种 工 况 及θ1=17°时d=800 mm、d=1 000 mm、d=1 200 mm三种工况下的流动情况。选取受工况改变影响较为显著的火箭芯级靠近助推器一侧的表面压力系数分布情况进行对比,结果如图8所示。

图8 不同工况下表面压力系数分布情况对比Fig.8 Comparison of pressure coefficient distribution at different conditions
从图8(a)中可以看出,随着头锥半顶角增大,来流受到的压缩程度变大,头锥处表面压力系数峰值出现位置逐渐提前,且峰值逐渐增大;从图8(b)中明显可以看到,激波与膨胀波来回反射压缩引起的压力系数震荡,随着芯级助推间距增大,干扰处表面压力系数峰值出现位置略微后移,对应的波动峰值也逐渐减小。图9给出标称工况下的马赫数云图及不同工况下的表面压力系数云图。
从马赫数及表面压力系数云图中可以看出,头锥处激波和膨胀波的干扰会导致冲击波后部产生倾斜的高流速区域,即低压区。而随着头锥半顶角增大,物面前端内折角度及后部外折角度均增大,导致激波波面倾角增大,头锥表面气流速度降低更快,气压波动幅度较大。芯级和助推间存在膨胀波(由于压缩来回反射的现象),当间距增大时,反射次数减少,表面压力系数及载荷变化都更加平衡,能量的损失也更小。单独从气动设计角度来讲,适当减小头锥半顶角、增大芯级助推间距更有利于载荷平衡变化,为结构设计降低不确定性。
4 结 论
1)针对带捆绑火箭气动载荷分布不确定的问题,提出了基于多项式混沌理论的捆绑火箭气动载荷灵敏度分析及不确定性量化方法,为结构设计提供更准确的需用载荷。
2)通过算例分析了来流马赫数、迎角及2个外形参数对气动轴向力和法向力峰值的灵敏度。结果表明,来流速度是影响轴向力的主要因素,而迎角是影响法向力的主要因素。头锥半顶角对头锥处的轴向力影响较大,芯级助推间距对二者产生气流干扰处的法向力有一定影响,但相对于马赫数和迎角影响不大。
3)通过非侵入式多项式混沌方法得到轴向力及法向力不确定性分布情况。结果表明,轴向力不确定性主要出现在头锥处,法向力不确定性主要出现在头锥及与助推器产生干扰处。头锥处的载荷不确定性主要原因是来流速度变化和头锥截面变化导致激波与膨胀波波角及强度不确定;助推干扰处的法向力不确定性主要由于来流条件及间距变化加剧了膨胀波反射波动。
4)头锥半顶角增大、芯级助推间距减小均会加剧芯级表面压力系数波动,增大气动载荷变化幅度。因此,为降低结构设计过程的载荷不确定性,可对气动外形参数设计提出一定建议,如适当减小头锥半顶角和增大芯级助推间距。
本文采用火箭半模型进行仿真计算,仅考虑了横向气动载荷影响,采用全模型可以综合分析横侧向气动载荷不确定性及来流方向与助推所在平面夹角变化对气动载荷的影响,后续将在本文基础上对此问题进行进一步研究。

