融合先验知识的BP神经网络锂电池剩余寿命预测*

郝可青，吕志刚，李 叶，邸若海，朱鸿杰

(1.西安工业大学 兵器科学与技术学院,西安 710021；2.西安工业大学 电子信息工程学院，西安 710021)

锂离子电池在军事应用中具有卓越的性能，因此广泛应用于单兵系统、卫星飞船以及无人战机等诸多兵种。然而在锂电池的循环使用中容易发生高温腐蚀老化以及电流电压参数的改变会导致锂电池设备出现故障，从而造成不可预估的损失。因此对锂电池进行剩余使用寿命(Remaining Useful Life,RUL) 预测是十分有必要的。目前，对于锂电池的RUL预测主要分为基于模型的预测方法和数据驱动的预测方法。由于数据驱动的方法具有更高的预测精度并且能够提高网络的泛化能力，因此通常选用该方法进行锂电池的RUL预测。

反向传播神经网络(Back Propagation Neural Network,BPNN)是1986年由D.Rumelhart和J.McClelland为首的科学家提出的概念，是一种按照误差逆向传播算法训练的多层前馈神经网络，是应用最广泛的神经网络[1]。它具有大规模并行、分布式处理、自组织、自学习等优点，已被广泛应用于语音分析[2]、图像识别[3]、计算机视觉[4]、模式识别与分类[5]、故障预测[6]等领域。

小样本问题广泛存在于各个行业中，广义上来讲，数据量少、样本结构不平衡、数据集信息覆盖率低都属于小样本问题，由于锂电池的加速老化试验周期长且可测量参数较少，因此得到的失效数据样本较少，且在小样本条件下构建的锂电池预测模型会存在过拟合等问题，故无法用传统的神经网络算法进行锂电池小样本数据的模型训练。文献[7]提出基于数据中心位置跟踪方法(Central Location Tracking Method,CLTM)的神经网络权值确定方法，实验证明该方法可以使用小数据集进行预测，但该方法随机性较大，需要多次实验才能准确验证。文献[8]提出基于先验知识约束和少量样本数据的Elman动态递归神经网络的算法，以混凝沉淀过程的两个约束条件和数据集进行了算法验证，但Elman网络存在训练速度慢和容易陷入局部极小值的问题。文献[9]提出基于线性先验的径向基函数神经网络算法，开发了基于广义约束线性神经网络-先验(Generalized Constraint Neural Network-Linear priors,GCNN-LP)的工具箱，但是难以适用于其他网络模型。文献[10]提出基于虚拟样本生成(Virtual Sample Generation,VSG)的神经网络算法，并利用加州大学欧文分校(University of CaliforniaIrvine,UCI)数据集验证了该方法的有效性，但如果真实数据具有相关属性，则该方法不能完全适用。文献[11]提出利用Bootstrap法和核密度拉丁超立方采样法扩充训练样本，利用扩充后的样本训练BPNN，在保障小样本自身规律的情况下，解决了小样本数据BPNN建模问题，但得到的参数结果都是随机变量，这导致模型的预测精度较差。文献[12]提出基于小样本的残差BPNN，通过将多个残差BPNN模块进行堆叠提高小样本BPNN预测精度，但设计过程过于复杂。通过对上述文献进行分析可得，解决小样本条件下BPNN建模的方法可分为两种：① 利用数据拟合模型或采样的方法进行数据扩充，构造合成样本，但该方法得到的数据随机性较大且质量并不高，导致模型的预测精度并不高；② 把先验知识作为已知的约束条件加入到神经网络的训练过程中，构建基于先验知识的神经网络建模方法。因此，文中提出融合先验知识的BPNN建模方法，以惩罚函数法的形式将单调性约束加入网络性能函数中，完成神经网络优化设计，并利用改进的粒子群算法(Particle Swarm Optimization,PSO)优化初始权值和阈值，可以提高网络的泛化能力以及避免网络陷入局部最优值。

1 算法思想

1.1 先验知识

先验知识指的是领域专家在对研究问题的机理有一定的了解。胡包钢等将先验信息定义如下：“先验信息是指在对目标系统实施建模或分析前就已知的任何相关信息(广义含义，包括知识、经验，常识和特定要求等)”[13]。常用的先验知识有单调性、凹凸性和等式约束等。实际生产中任何复杂的数学关系，都可以将其某个区间划分为具有单调关系的区段，然后利用单调性来进行处理。

如果在区间[x1,x2]内都存在函数f(x)，那么单调性的数学定义为

(1)

式(1)中若输入输出满足该单调性关系，则称f(x)在此区间为单调递增函数。

因此，文中将单调性作为先验知识，通过增加单调性信息来增加小数据集条件下BPNN训练可获得的信息量，使训练所得模型更加真实有效，提高模型预测精度。

1.2 权值阈值更新

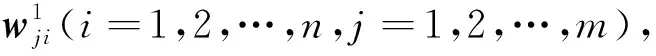
(2)

式中：w1为输入层到隐含层的权值矩阵；w2为隐含层到输出层的权值矩阵。

网络均方误差为

(3)

将输入pi与输出Y呈单调递增的约束条件Ci进行数学推导，得到的结果为

(4)

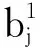
根据最优化原理中的惩罚函数法，将单调性作为先验条件引入网络，对神经网络模型训练产生的输出数据进行单调性判断。如果实际数学关系是单调递增(递减)的，神经网络训练结果也是单调递增(递减)的，那么说明符合这次训练过程先验知识，不加惩罚，如果判断后结果与实际值相反，则给予惩罚处理。因此，性能函数应该由两部分组成：① 最小均方误差，其作用是尽量使实际输出逼近目标值；② 约束项，惩罚函数的作用是尽量满足先验知识约束。重新定义的网络性能函数f(e)为

f(e)=L(e)+μCi,

(5)

式中:Ci的取值为

(6)

式(5)中e为误差输出，μ为惩罚因子决定了第二部分对性能影响的权重。μ取0时，忽略约束；μ取的越小，训练所得模型越容易违背先验知识；μ取值越大，训练所得模型越不容易违背先验知识，但训练所得实际输出与目标值会有一定的偏差。

当Ci>0时，即当输入输出满足单调递增条件时，权值阈值更新为

(7)

式中：k为当前隐含层节点个数；α为学习速率。

当Ci≤0时，即当输入输出违背单调递增条件时，权值阈值更新为

(8)

由式(4)得

(9)

设网络训练算法采用最小均方误差算法，则最终权值阈值更新为

(10)

1.3 优化初始权值阈值

由于初始权值和阈值的好坏会影响BP网络训练的时间和精度，“坏”的初始参数可能使BPNN训练陷入局部最优。因此，现有方法多将粒子群算法的全局寻优能力与BP算法的局部寻优能力相结合，利用粒子群算法来优化神经网络的拓扑结构、连接权值和阈值，以提高神经网络的泛化能力和学习性能。

实验证明，粒子群算法中的惯性权重系数w的数值较大时能够增强粒子进行整体搜索能力，惯性系数W数值较小时能够增强粒子进行局部搜索能力[14]。为了权衡粒子局部搜索以及全局搜索的能力，文中将自适应权重和线性递减权重结合提出改进的粒子群算法W-PSO来优化神经网络的权值和阈值。W-PSO算法的具体表达如下：

设搜索空间是D维，那么第i个粒子的位置可表示为Xi=(xi1,xi2,…,xiD)，速度可表示为Vi=(vi1,vi2,…,viD)，个体最优极值为Pi=(pi1,pi2,…,piD)，全局最优极值为Gi=(gi1,gi2,…,giD)，i表示粒子的个数即i={1,2,…,m}，VK+1为第K+1个的粒子速度与位置的更新为

VK+1=WVK+c1r1(PK-XK)+c2r2(GK-XK),

(11)

XK+1=XK+VK+1,

(12)

(13)

式(11)～式(12)中c1,c2为加速因子；r1,r2为随机数，一般取值在[0,1]之间；Wmax为开始时的惯性权重；Wmin为迭代数目达到最大值时的惯性系数；f是当前的适应度值；favg为平均适应度值；fmin为最小适应度值；Tmax为迭代次数最大值；K为当前的迭代次数;PK为当前个体最优极值；XK，XK+1分别为第K和K+1个粒子的位值；GK为当前全局最优极值。

1.4 算法流程

融合W-PSO和单调性约束的BPNN算法步骤为

① 确定BPNN网络结构，根据网络的结构初始化粒子种群及参数；

② 根据式(11)～式(13)计算W-PSO算法的粒子适应度值，寻找个体最优值和种群最优值；

③ 判断是否满足终止迭代条件，若满足，则对其进行解码，获得优化的权值和阈值，若不满足，则更新粒子速度和位置，返回②，重新寻找最优值；

④ 根据式(2)～式(6)计算网络输出和添加约束的惩罚项系数大小；

⑤ 判断是否满足单调性约束，若满足跳转到⑥，若不满足跳转到⑦；

⑥ 计算式(5)，采用式(7)更新权值阈值；

⑦ 计算式(5)，采用式(10)更新权值阈值；

⑧ 判断是否达到目标精度和最大循环次数，重复④～⑦，直至满足要求，结束网络训练。

2 仿真结果

2.1 W-PSO算法仿真对比

图1表示当种群个数为50，最大维数为50，最大迭代次数为500，c1=c2=2，Wmin=0.4，Wmax=0.9时，文中所提算法W-PSO和原始自适应权重PSO-adaption算法、线性递减权重PSO-linear算法在测试函数Sphere Model和Generalized Griewank上的对比结果。其中Sphere Model为非线性的单峰单极值函数，原点取最小值时，其f表达式为

(14)

Generalized Griewank为多峰多极值函数，原点取最小值时，表达式为

(15)

由图1可知，与PSO-adaption算法和PSO-linear算法相比，文中所提W-PSO算法具有更快的收敛速度和更高的收敛精度。

图1 三种PSO算法的测试结果对比

2.2 算法仿真及对比分析

2.2.1 先验知识的获取

为了验证W-PSO算法的性能，文中使用Matlab 2020a实现网络模型的构建和训练，操作系统为Windows 10，内存16 GB。文中实验采用美国国家航空航天局(National Aeronautics and Space Administration,NASA)锂离子电池性能退化试验数据集[15]进行算法验证和模型比较，该数据库选用18650锂离子蓄电池进行循环充放电的老化试验，循环充放电导致锂离子电池的性能发生退化，造成实际电池容量衰减，每个完整的充放电周期包含充电、放电和阻抗测量三个工作过程。实验过程如下：① 锂离子电池在电流为1.5A恒流状态下进行充电，电压上升至4.2 V，在恒压模式下继续保持充电状态，直到充电电流降至 20 mA，则表示充电已经结束； ② 锂离子电池在恒流模式下进行放电，直到电压达到设定的某一截止电压时停止放电；③ 实验测量锂离子电池的阻抗通过EIS 频率扫描来实现，通常设置扫描范围为0.1～5×103Hz。

文中将电池容量C作为锂离子电池性能退化的直接健康因子，以F1～F5指标为间接影响因子，构建BPNN。F1,F2分别表示为等压升、等流降充电时间间隔，F3表示为等压降放电时间间隔，F4,F5分别表示为充电、放电过程中的平均温度。

其中第一个和第二个间接健康因子是从锂电池的恒流/恒压充电曲线中提取的。如图2(a)所示，在恒流充电过程中，电压从较低的值升为较高的值，取这一阶段为F1。如图2(b)所示，在恒压充电过程中，电流从较高的值下降为一个稳定值，这一阶段为F2，锂电池的总充电时间会随着电池容量的衰减而逐渐缩短。由于在实际情况中，存在着不完全充放电的现象，故F1是人工设定的两个电压之间的时间间隔，F2也是人工设定的两个电流之间的时间间隔。

图2 F1,F2,F3间接影响因子提取

类比F1和F2的提取方法，从电池的放电电压曲线中提取等压降放电时间间隔为F3，如图2(c)所示，可明显看出等压降放电时间间隔随着充放电周期的增长而呈现递减的趋势。将充放电过程中的平均温度作为F4和F5，可以使得在线容量的估计更为简便，图3(a)所示为F1开始时刻到F2结束时刻之间的电池平均温度，图3(b)所示为F3时间段内的电池平均温度。

通过对数据进行处理获得先验知识，如图4所示。

图3 F4,F5间接影响因子提取

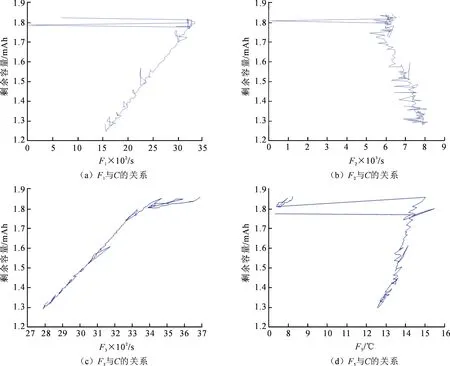
图4 获取的先验知识

其中，图4(a)表示F1与C呈单调递增关系；图4(b)表示F2与C呈单调递减关系；图4(c)表示F3与C呈单调递增关系；图4(d)表示F5与C呈单调递减关系。由图4可知，获得4条先验知识均可添加到BPNN的训练中，其中，F4与C并不存在单调性关系。

2.2.2 预测误差对比

以增加一条先验知识为例，证明所提算法的有效性。图5为当惩罚因子μ=1，训练集为40和30，增加F1与C单调递增约束和W-PSO，128和138个测试集的预测结果。图6为当惩罚因子μ=0.1和μ=0.5，训练集为40，增加F1与剩余容量C单调递增约束和W-PSO，128个测试集的预测结果。其中，预测结果的好坏以平均误差R(R=均方误差SSE/测试样本个数)的大小进行衡量，R越小，预测误差越小，算法性能更优。

图5 不同算法预测平均误差对比

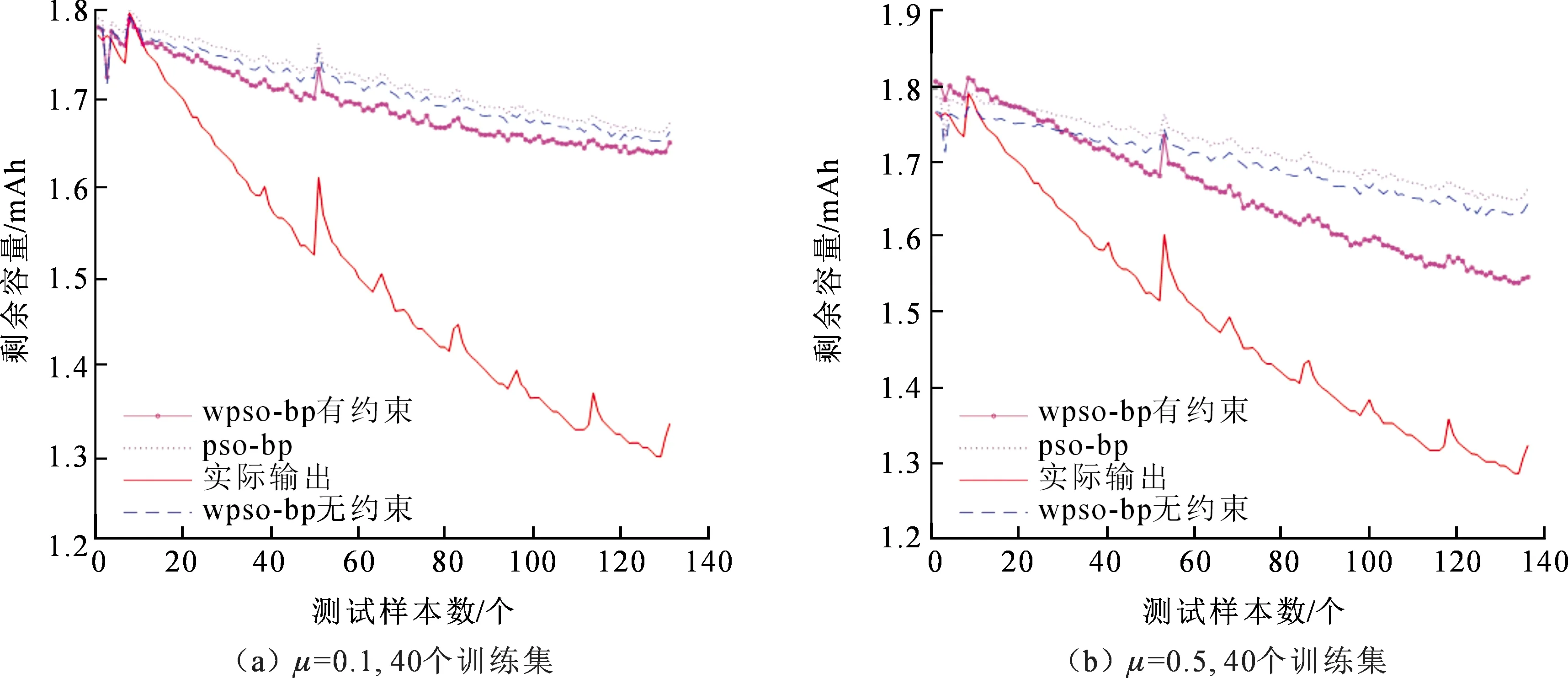
图6 不同算法预测平均误差对比

由图5可看出，标准PSO-BP算法的平均误差R1最大，W-PSO无约束条件算法的平均误差R2次之，文中所改进的W-PSO有约束条件算法的平均误差R3最小，即文中算法在锂电池数据为小样本条件下具有更好的预测性能。

由图6可知，惩罚因子μ的大小会影响文中算法性能，μ越大预测误差越小，μ值的取值范围可通过均方误差的量级确定。当μ取值不同时，所对应的误差见表1，其中R13表示W-PSO无约束的条件下与W-PSO有约束的条件下的差值，其中R23表示标准PSO的条件下与W-PSO有约束的条件下的差值。

表1 平均误差分析

3 结 论

文中通过将先验知识添加到BPNN的性能函数中以此提高锂电池剩余使用寿命预测模型的精度以及增强网络的鲁棒性，可得到以下结论：

1) 构建自适应变化的惯性权重系数，提出W-PSO算法，将先验知识以单调性约束的形式加入到BPNN性能函数中。

2) 利用W-PSO算法能够增强权衡局部搜索以及全局搜索的能力，避免网络陷入局部最优解，当模型的训练集个数相同时，误差随着约束项系数的增大而减小。

3) 采用NASA锂电池失效数据集，通过实验对比分析文中所提算法与其他常用锂电池寿命预测算法，可得文中算法构建的模型平均误差下降了5%，具有更高的预测精度，且该方法可与大样本条件下的模型预测方法进行对比分析研究。