基于二维统计分析的降水粒子分类方法
李 海, 张超群, 郭生权, 冯 青
(中国民航大学天津市智能信号与图像处理重点实验室, 天津 300300)
0 引言
降水粒子分类研究对于灾害天气的识别、预警、数值预报以及人工影响天气的作业指挥和效果评估都有十分重要的意义。与传统多普勒气象雷达相比,双偏振气象雷达可以交替发射水平和垂直偏振波,并接收2个偏振方向的回波信号,除获取反射率强度、径向速度、速度谱宽外,还可探测差分反射率因子、差分传播相移、相关系数等参量,具有识别粒子相态功能,是近年降水粒子分类研究领域的研究热点。
模糊逻辑方法是最经典的降水粒子分类方法,是一种解决不精确和不完全信息问题的有效方法, 最大的特点是可以利用专家经验进行分类,能够比较自然地处理模糊的概念, 其主要的优点是可以处理不确定的信息。20世纪90年代初,Straka等将模糊逻辑应用于双偏振雷达的降水粒子相态识别研究中,与经典布尔逻辑方法相比,模糊逻辑方法以隶属函数代替经典布尔逻辑的固定阈值,同时减少了判断步骤。Zrnic等将隶属函数由二维矩阵变成了5个极化参量的矩阵,同时可以识别9种降水粒子。曹俊武等将模糊逻辑方法应用于国内的双偏振雷达。Park等改进了模糊逻辑相态识别算法(Hydrometeor Classification Algorithm, HCA),将隶属函数修改为非对称的梯形,并引入了置信向量来平衡数据误差。
近几年,基于模糊逻辑的双偏振气象雷达方法在国内应用开始兴起。文献[5]中利用模糊逻辑算法对上海的S波段双极化气象雷达实测数据进行降水分类的业务分析。文献[7]中利用模糊逻辑算法对X波段双极化气象雷达探测降水数据进行分类,分析研究了各降水粒子在雷暴演变过程中的相态特性。汪舵等建立了一种基于相态识别的S波段双线偏振雷达最优化定量降水估测算法。文献[9]以美国HCA方法为基础,建立了适合广东S波段双偏振气象雷达的分类方法。武崇等对一次超级单体进行讨论,用HCA方法识别出雨及冰雹混合物区域。同年,他通过对飑线过程的分析,对HCA算法的参数和阈值进行优化,得到适用于华南珠海的偏振算法,该研究为发展适合中国降水特征的 HCA 算法奠定基础。王洪等将Park的算法简化并应用于珠澳偏振雷达中,通过S波段雷达对一次超级单体进行分析,有效识别出冰雹区域,由于仅对一次观测结果得出结论,因此对各偏振量之间的定量关系也需要进一步研究。杨章等基于HCA-LIQ算法对广州9次降雨评估,由于该算法低估了中小颗粒的沉淀,过高估计了中等和大颗粒的沉淀,导致对大雨的分类不准确,需要研究极大雨来进一步验证并改进算法。冯亮等利用双偏振气象雷达数据建立了基于偏振参量、温度、纹理参数的模糊逻辑降水粒子识别算法。文献[14]基于深度学习和模糊逻辑算法对降水粒子进行分类,该方法提高了水凝物识别的准确性。王金虎等利用模糊逻辑算法和神经网络算法对云雷达联合微波辐射计探测数据进行降水粒子分类研究,结果表明模糊逻辑算法对退极化比极为敏感。发展至今,模糊逻辑方法仍存在一定的局限性,例如怎样确定隶属函数参数,以及如何提高降水粒子分类的准确率。
本文使用二维统计分析的方法确定钟型隶属函数的参数。首先将数据进行二维统计,分析得到钟型隶属函数的参数中心以及宽度的取值,然后取隶属函数图像的临界值作为钟型隶属函数斜率。再根据不同极化参数对降水粒子的贡献程度以及分类准确率调节各极化参数的权重系数。最后使用调节好的参数以及权重系数对一次雷达数据进行降水粒子分类。该方法能够较为准确的调节隶属函数参数,实现降水粒子分类。
1 基于二维统计分析的模糊逻辑降水粒子分类方法
模糊逻辑方法是最经典的分类方法,主要分为3个部分:模糊化、规则计算和退模糊。模糊化主要是对隶属函数参数的确定,而隶属函数参数和权重系数直接影响规则计算的准确率,从而影响退模糊后的降水粒子分类准确率,退模糊中引入融化层信息调节降水粒子分类结果。隶属函数参数一般是使用专家经验值进行确定,不同隶属函数的参数也不同,本文使用二维统计分析方法对钟型隶属函数参数进行确定,使用模糊逻辑方法实现降水粒子分类,流程如图1所示。在模糊化过程中,首先对带标签的不同降水粒子各极化参数的数据进行处理,然后对处理后的数据进行二维统计分析,对钟型隶属函数的中心、宽度进行确定,再取临界值作为斜率的取值;在规则计算过程中,调节不同降水粒子各极化参量的权重系数,得到参数调整的结果;最后将调节好的参数使用模糊逻辑方法对一次雷达数据进行降水粒子分类。
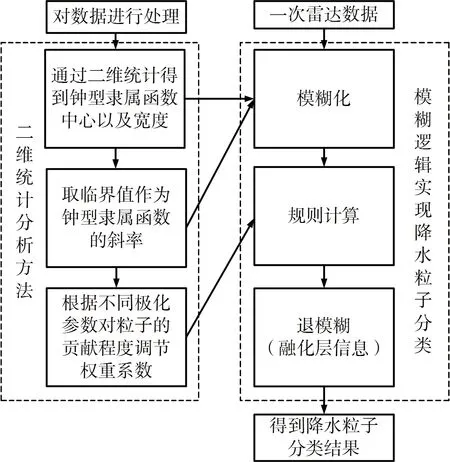
图1 总体流程图
1.1 数据处理
本文使用4个极化参数进行识别、分类:水平反射率因子,差分反射率因子,互相关系数和差分相移率,其中差分相移率取对数形式。
1) 水平/垂直反射率因子/(单位:dBz)
双偏振气象雷达发射水平和垂直偏振方向电磁波,通过雷达的回波数据可以计算得出水平反射率因子和垂直反射率因子。
2) 差分反射率因子(单位:dBz)
差分反射率表示为和的差,计算方式为
=-
(1)
反映了降水粒子下落过程中的形变程度,形变程度与降水粒子的空间取向和轴比(粒子的长轴与短轴的比值)有关,粒子形状越接近圆球形时的值越接近于0。
3) 互相关系数
是水平和垂直偏振波的后向散射特征的相关性。定义为水平与垂直偏振回波信号的互相关系数。
4) 差分相移率(单位:(°)/km)
不受雷达定标、衰减和波束遮挡等影响,在液态的降水粒子中一般为正值,在垂直取向的柱状冰晶处会出现负值。由于参量较大的变化范围不利于降水粒子的相态识别,因此在的基础上引入了,即使用对数坐标替代线性坐标,具体如下:
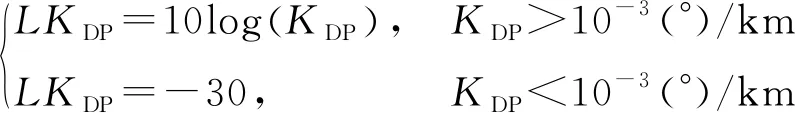
(2)
1.2 二维统计分析方法确定钟型隶属函数参数
1) 钟型隶属函数
不同降水粒子类型各极化参量的范围通常以适当的隶属函数为特征,本文使用钟型隶属函数,一方面,钟形隶属度函数具有扁平宽阔的区域,它对应于降水粒子的参数取值范围,而不是单一的数值;另一方面,钟形隶属度函数有一个很宽的过渡区,可以改善模糊逻辑识别算法在过渡区的可靠性。钟型隶属函数表达式如式(3)所示:
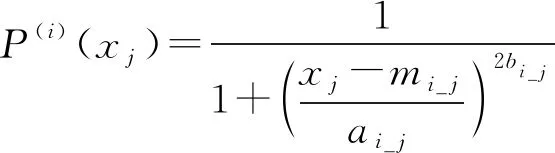
(3)
其中,=1,2,…,6,代表6种分类结果,本文将双偏振雷达回波识别为6种降水粒子分类:1)冰晶(IC);2)干雪(DS);3)湿雪(WS);4)雨(RA);5)霰(GR);6)冰雹(HA)。=1,2,3,4,代表有4种用于相态识别的雷达极化参量,代表4种极化参量,分别是:1);2);3);4)。_是隶属函数的中心,_是隶属函数宽度的一半,_是隶属函数的斜率,每个参数的意义如图2所示,横坐标代表极化参数,纵坐标代表隶属度,其中,不同的分类结果的各极化参数有不同的隶属函数范围。
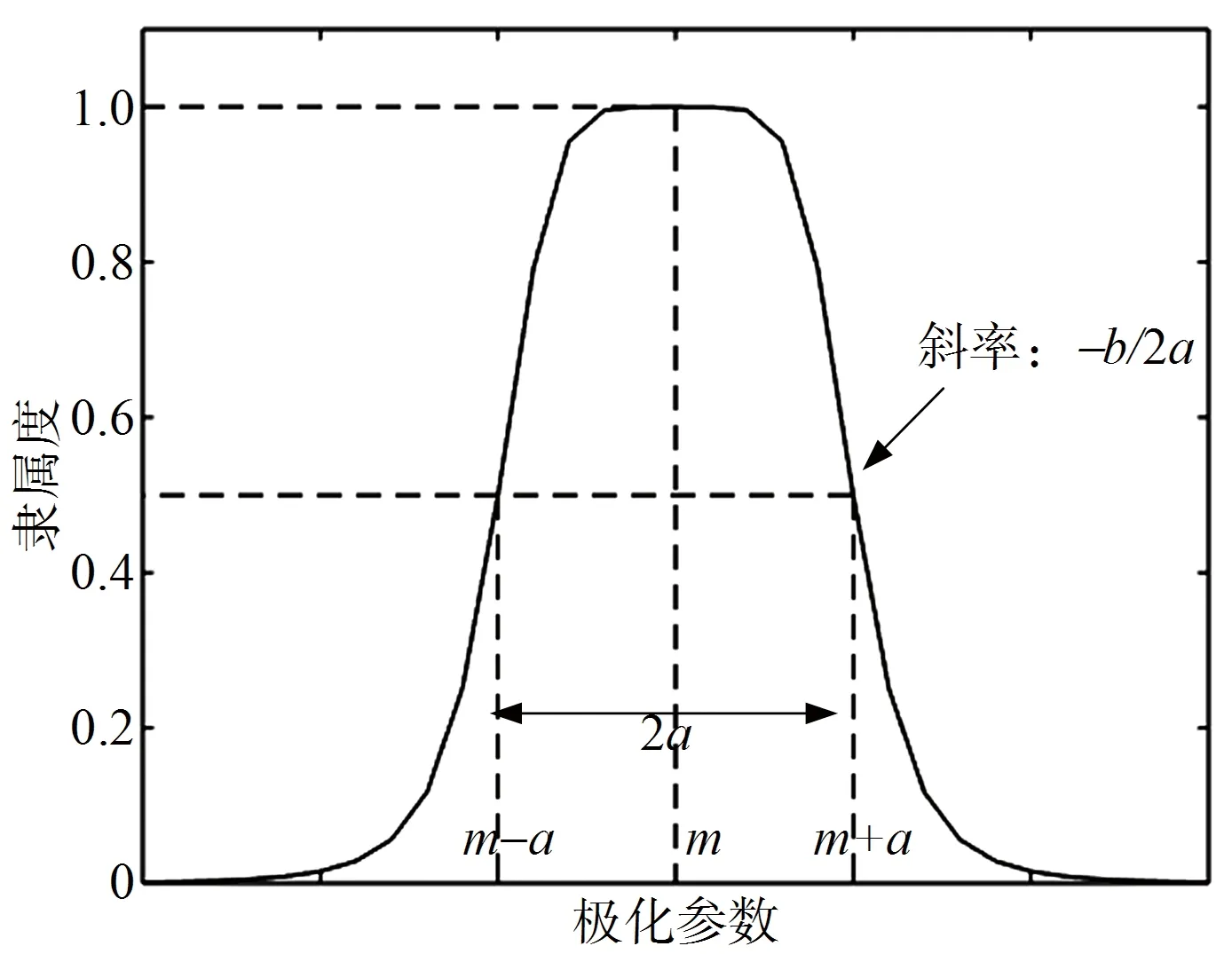
图2 钟型隶属函数
2) 中心值_及宽度_的确定方法


(4)
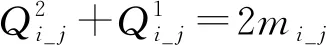
(5)
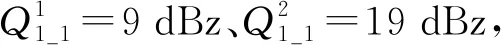
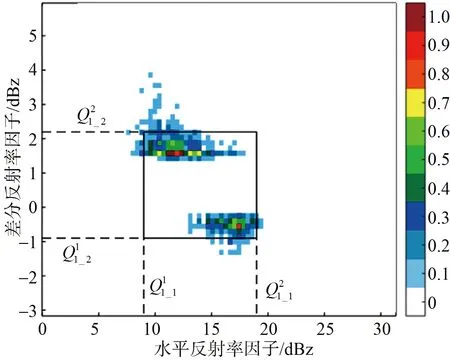
图3 冰晶ZH_ZDR频次图
3) 斜率_的确定方法
斜率的取值一般是0~20范围内的数字,斜率太小,不同降水粒子的隶属函数重叠区域比较大;斜率太大,钟型隶属函数所包含的区域几乎不会发生变化,因此,本文分别将HA和RA、DS和IC、WS和GR的隶属函数对比,先画出斜率值为0.5时的钟型隶属函数图像,然后不断以0.5~1的间隔增大斜率的取值,得到多个隶属函数图像,经过对斜率取值的调整使钟型隶属函数所包含区域几乎不会发生变化,确定临界值,取临界值作为斜率_。
图4代表HA和RA的的钟型隶属函数,实线代表HA的隶属函数,虚线代表RA的隶属函数,不同颜色代表不同斜率的取值。由图可得,当HA斜率为2,RA斜率为4时,钟型隶属函数之间重叠区域较大,当HA的斜率大于10,RA的斜率大于12时,钟型隶属函数区域不会发生变化,所以选取HA的钟型隶属函数斜率为=10,RA的钟型隶属函数斜率为=12。

图4 HA和RA的水平反射率因子(ZH)隶属函数(实线:红色斜率为2,蓝色斜率为3,绿色斜率为5,蓝绿色斜率为8,黑色斜率为10,紫红色斜率为12;虚线:红色斜率为4,蓝色斜率为6,绿色斜率为8,蓝绿色斜率为10,黑色斜率为12,紫红色斜率为13)
1.3 权重系数Wij确定方法
权重系数一般由综合理论值与专家的经验确定,本文以文献[6]给出的权重系数为参考,如表1所示,权重系数的取值一般是0,0.2,0.4,0.6,0.8,1.0。根据极化参数对降水粒子识别的贡献程度高低以及分类结果准确率调节权重系数大小,提高识别能力更强的极化参数的权重能有效提高准确率。本文根据极化参数的贡献程度来调节权重系数大小,并使用混淆矩阵来判别不同分类结果的准确率,取准确率最高的权重系数作为最终的调整结果。
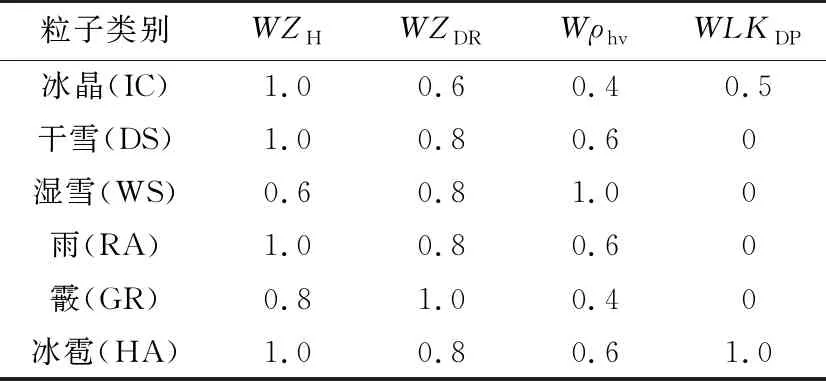
表1 原始权重系数
混淆矩阵如图5所示,横坐标代表修改参数后的分类结果,纵坐标代表数据的标签,对角线代表不同类别的准确率。图5(a)是未调节权重系数的分类结果准确率,识别效果不好的IC与DS主要在隶属函数区域内更容易区分,在、、隶属函数区域重叠,因此,试验将IC的权重系数改为0.8,0.6,0.2,将DS的改为0.8,1.0,0.4,统计混淆矩阵的准确率,将准确率最高的结果对应的权重系数作为权重系数调节后的结果,确定将IC的权重改为0.6,DS的改为1.0。同理,HA和RA主要依靠隶属函数区域进行识别,考虑到HA的的权重已最高,仅修改RA的权重,试验将RA的改为1.0,0.6,0.4,0.2,统计混淆矩阵的准确率,确定将RA的权重系数改为0.6。WS和GR在隶属函数区域内更容易区分,考虑到权重系数已经最大,试验将GR的权重改为0.8,0.6,0.2,统计混淆矩阵准确率,确定将GR的权重改为0.6。由图5(b)可知,修改权重系数后,除雨外的其他降水粒子准确率均有所提高,说明调整权重系数后,结果更加准确。

(a) 未调节权重准确率
1.4 双偏振气象雷达模糊逻辑降水粒子分类方法
模糊逻辑方法本质是简单的规则运算,其主要是将各极化参数对降水粒子的判别信息进行规则运算,得到分类结果,主要分为3个步骤进行分类:模糊化、规则计算和退模糊。
模糊化是将极化参数对应于不同降水粒子的特定范围,本文使用二维统计分析方法确定钟型隶属函数参数,并使用钟型隶属函数表示不同降水粒子各极化参数的范围。
规则计算是模糊逻辑最重要的一步,使用隶属函数的加权求和实现分类,在此过程中,主要确定权重系数的取值,本文通过混淆矩阵代表准确率来调节权重系数,使规则计算的结果更加准确,提高降水粒子分类准确率。函数表示来自所有分类的总贡献,公式如式(6):

(6)
其中()()是钟型隶属函数,表示第类极化参数的范围;=4,代表4个极化参数;表示某一类的权重系数。
最后是退模糊,比较不同分类的并找到具有最大值的类,作为最终输出结果,其中=,代表6种降水粒子。在实际中,此过程应考虑一些物理约束。对于降水粒子分类,最常见的约束来自融化层。根据融化层顶部高度和底部高度,计算波束中心和-3 dB波束宽度与融化层的相对位置,得到雷达波束在融化层上下界、的投影距离、、、。
根据融化层的边界以及融化层的温度信息,对降水粒子分类结果做一定的限制:雪只能出现在融化层底部及以上的高度;纯雨仅能出现在融化层顶部及以下的高度。根据上述原理,在不同距离范围内可以存在的降水粒子如表2所示。

表2 不同距离范围内存在降水粒子类型
本文通过二维统计分析方法对模糊逻辑钟型隶属函数参数修改,调节权重系数,并引入融化层信息对一次雷达数据进行分类,得到降水粒子分类结果。
2 算法流程与步骤
基于二维统计分析的模糊逻辑双偏振气象雷达降水粒子分类方法具体实现步骤如下:
步骤1 对数据进行处理,得到本文所需的4种极化参量;
步骤2 根据数据进行二维统计分析,确定钟型隶属函数参数;
步骤3 根据极化参数对降水粒子识别的贡献程度高低以及分类结果准确率调节权重系数大小;
步骤4 利用调节后的参数,并引入附加信息使用模糊逻辑方法对一次雷达数据进行降水粒子分类。
3 实验结果及分析
3.1 参数调整结果
1)中心_以及宽度_的取值
对不同分类结果数据进行二维统计分析,得到不同极化参数的频次图,再根据图6~图11 的边界值计算得到不同降水粒子各极化参数的隶属函数参数:中心_和宽度_。

图6 IC频次图

图7 DS频次图

图8 WS频次图

图9 RA频次图

图10 GR频次图

图11 HA频次图
2) 斜率_的确定
不同降水粒子各极化参数的钟型隶属函数图如图12~图14所示,斜率太小,不同降水粒子的隶属函数重叠区域比较大;斜率越大,钟型隶属函数所包含的区域几乎不会变化,所以取临界值作为最终的斜率_。
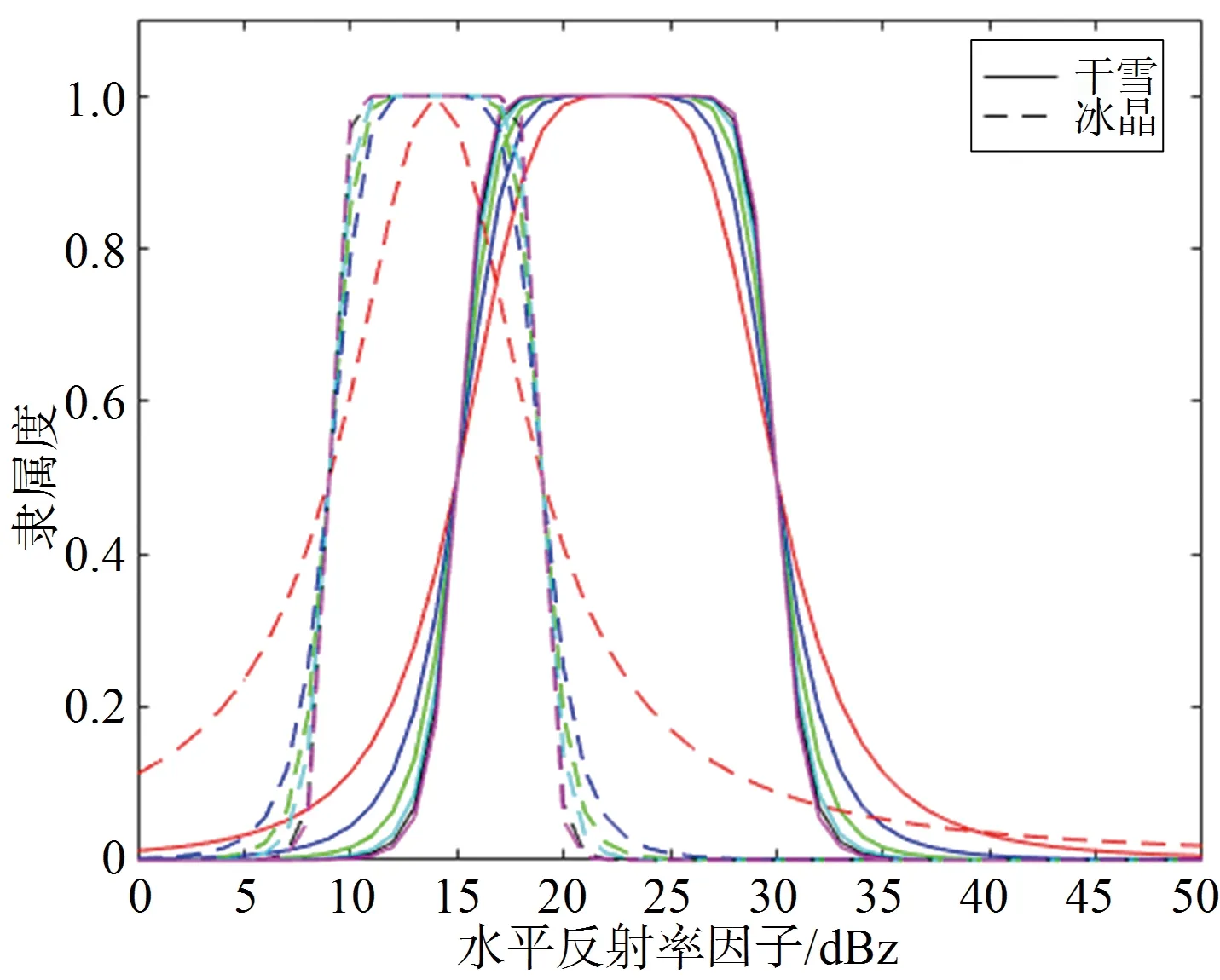
(a) ZH不同斜率时隶属函数图像
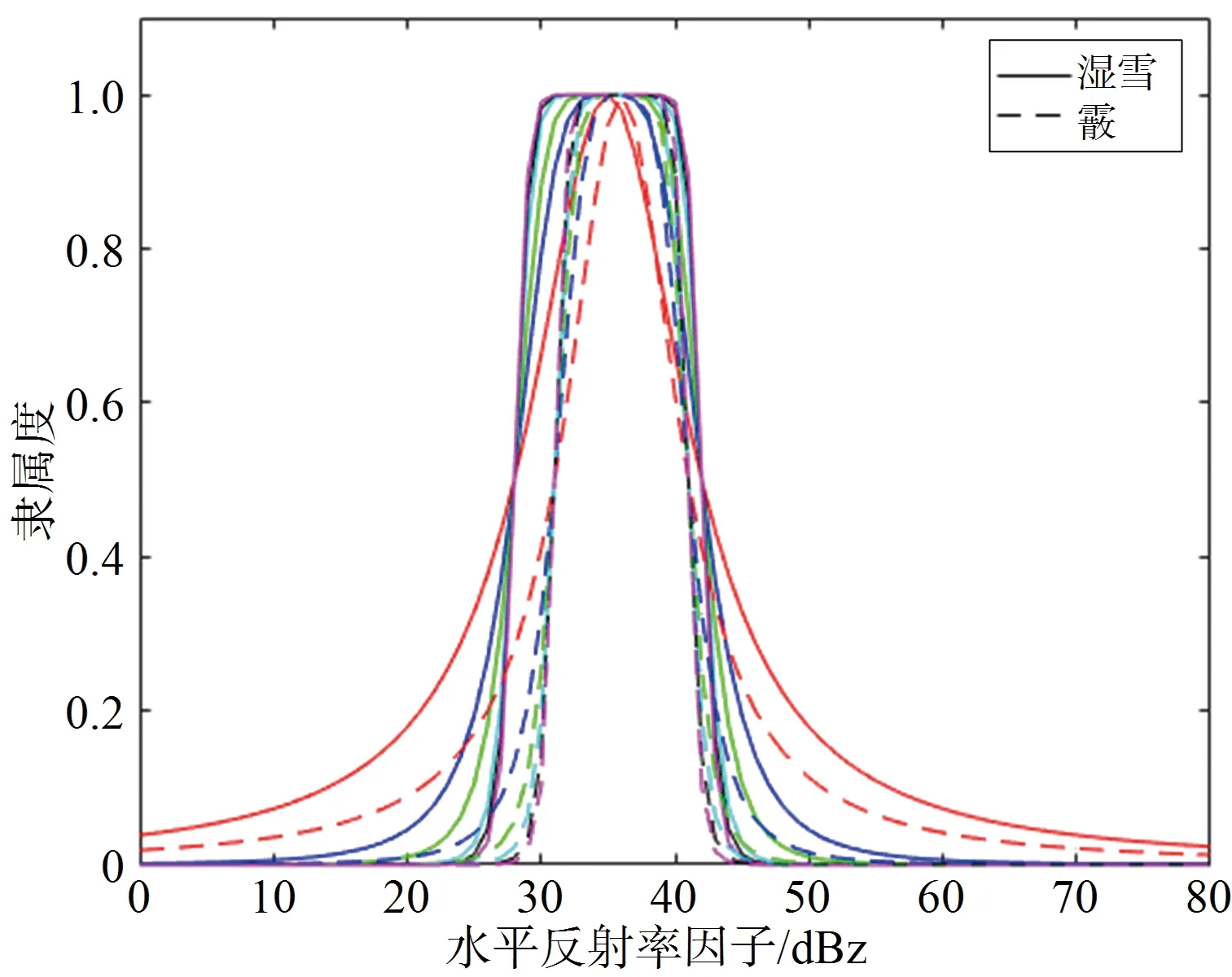
(a) ZH不同斜率时隶属函数图像

(a) ZH不同斜率时隶属函数图像
3) 钟型隶属函数参数取值
通过数据分析确定参数,得到模糊逻辑钟型隶属函数参数取值如表3所示。

表3 钟型隶属函数参数修正值
4) 权重系数取值
权重系数是为了显示不同极化参数对不同降水粒子的贡献程度,通过混淆矩阵表示准确率来调整权重系数,调整后的权重系数如表4所示。

表4 隶属函数权重系数
3.2 降水粒子分类结果
选取KTLX雷达2019年6月9日当地时间14:55数据,利用调节参数后的模糊逻辑方法进行降水粒子分类。图15(b)是调节参数后模糊逻辑的分类结果,同时与NOAA提供的降水粒子分类结果(图15(a))作为对比和参照。从图15(a)和图15(b)的对比中可以看出:调节钟型隶属函数参数后,模糊逻辑方法与NOAA提供的分类结果相似,仅存在一定程度的误识别,对于冰雹来说,识别区域要比NOAA提供的区域大,把少量的雨分为了冰雹。总体来说,与NOAA提供的结果相似度比较高。
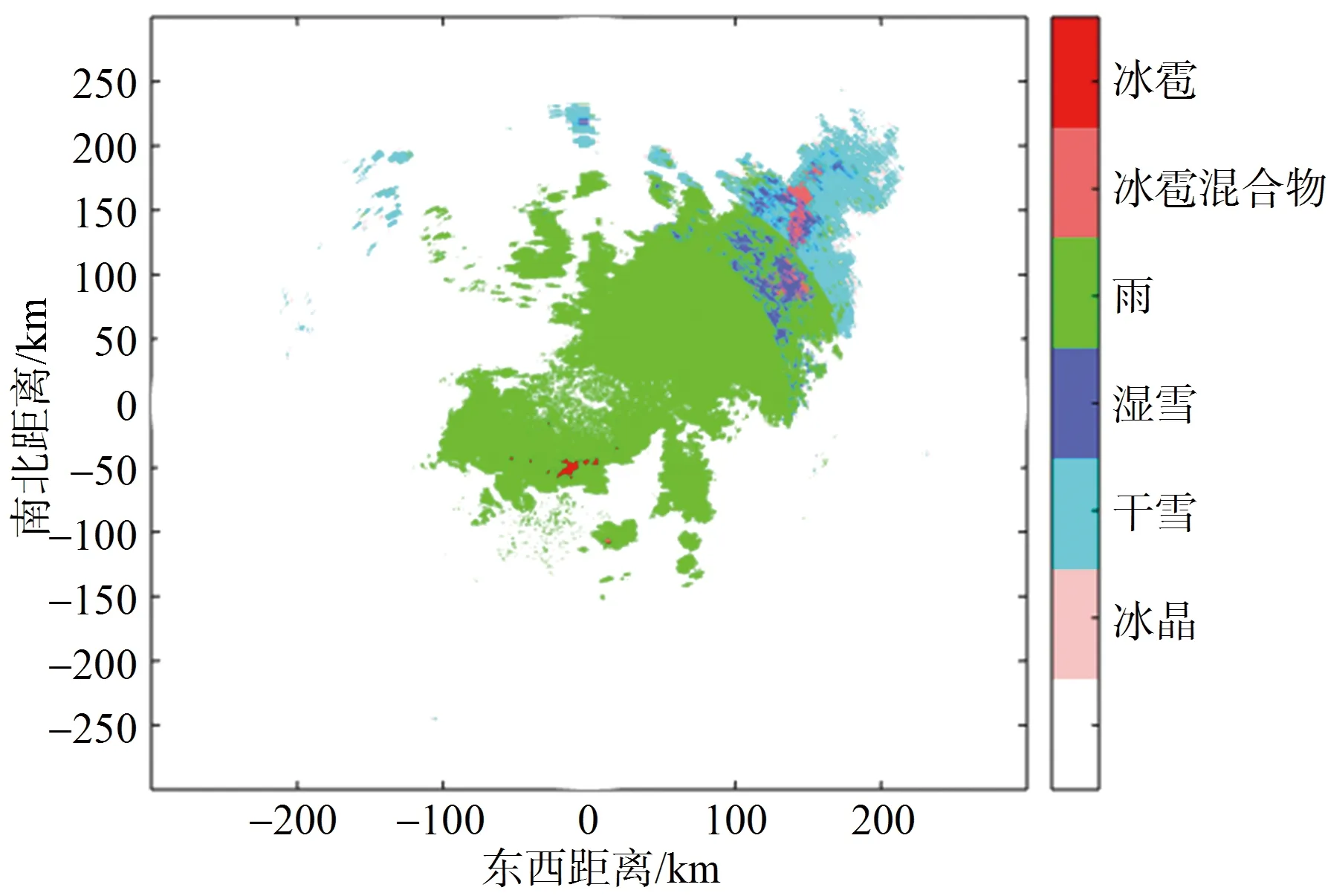
(a) NOAA提供结果
4 结束语
针对模糊逻辑钟型隶属函数参数确定问题,本文使用二维统计分析的方法来确定钟型隶属函数的参数。首先将双偏振气象雷达的极化参数进行二维统计分析,得到钟型隶属函数参数:中心以及宽度,然后将临界值作为钟型隶属函数的斜率。再根据不同极化参数对降水粒子的贡献程度以及准确率调节降水粒子每一类极化参数的权重系数。使用调节好的参数以及权重系数对一次雷达数据进行降水粒子分类,实验结果表明,该方法能够较为有效地实现降水粒子分类,具有很好的研究潜质和应用价值。

