网络视角下基于夏普比率的投资组合策略
赵 霞,时 雨,王佳琪
(1.上海对外经贸大学 统计与信息学院,上海 201620;2.兰卡斯特大学 数学与统计学院,兰卡斯特 LA1 4YW)
一、引 言
投资组合理论与实践一直是近年来学界和业界关注的热点问题之一,其对资产的保值增值和风险管理起重要作用。根据波士顿咨询统计数据,截至2020年底全球资产管理规模已达到103万亿美元;截至2021年上半年,中国资产管理规模约110亿元, 成为仅次于美国的全球第二大资管市场。因此,投资策略问题的研究有助于服务国家及社会发展需求,对促进金融市场健康发展、推动经济发展具有积极的现实意义。
随着金融一体化和经济全球化的发展深化,金融市场行为的复杂性和多样性表现得越来越显著,牵一发而动全身,各资产间的相互关联性在投资组合策略选择及金融风险管理中起关键作用。近年来学者们开始考虑将金融市场视为一个复杂网络系统。从网络的视角去刻画资产之间的关联和影响,进而探讨相应的投资组合问题,可以更全面、深入地把握资产间的内在关系,在资产配置、资金链风险传播、风险控制与监管等方面提供更科学的管理决策。
Markowitz提出了考虑投资组合的收益和风险两方面特征的优化模型——均值-方差模型。随后,有大量文献关注改进投资组合优化模型的优化准则,例如,均值-绝对离差准则、均值-半方差准则、均值-方差-CVaR准则等等。Sharpe提出了夏普比率最大化准则,其中夏普比率定义为投资组合超额回报与其标准差的比值。容易看出,通过最大化夏普比率,投资者能够在优化问题的目标函数中同时考虑投资组合回报和风险,且具有良好的经济解释。宋红雨分析了在非卖空条件下,夏普比率在投资策略中的应用。周明等基于最大化夏普比率准则研究了保险公司的最优再保险策略。Sahamkhadam等结合GARCH-EVT-Copula模型在最大化夏普比率准则下进行了投资组合优化研究。Zhao等基于谱风险测度和最大化RAROC准则研究了最优保险投资策略问题。
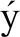
综上,本文将考虑用最大化夏普比率作为优化准则,选取四种不同的相关系数刻画资产间相依关系来构造资产相依网络,研究最优投资策略问题,并与全局最小化风险准则下的策略进行对比分析。实证分析基于上海证券交易所的部分股票和基金数据,利用滚窗法(内样本窗宽分别设定为一年和两年)得到了动态调整的最优投资组合,并进一步分析了最优投资组合的内样本权重结构及外样本绩效表现。
二、相依网络与优化模型
假设投资者投资于个资产,资产的收益率向量为=(,…,)′,投资者的投资权重向量为=(,…,)′。∑与分别表示收益率向量的方差-协方差矩阵及均值向量,而=′∑与=′分别表示投资组合的方差和期望收益。
(一)相依网络及互联矩阵
参照Clemente 等,通过四种相关系数来构造相依网络,并进一步构造可以从系统角度刻画资产间风险关联性的互联矩阵。
金融市场可以视作一个网络,其中每个资产作为一个网络节点,个节点的集合为,为所有节点间边的集合,则金融市场可由=(,)所表示。这里我们假定为有权无向网络,即任一节点与节点间仅有一条无指向的边(,)连接,且边上附有权重∈。用如下四种相关系数来量化:
(1)皮尔逊相关系数(,)被广泛地应用于刻画资产间的线性相依关系。
(2)考虑资产间的非线性相依关系,Kendall’s tau相关系数(,)及斯皮尔曼相关系数(,)具有良好的捕捉能力,具体讨论见Puth 等。
(3)为了刻画资产间的尾部相依关系,我们选用下尾相依系数(,)来刻画资产较大损失部分之间的相依关系,具体讨论见Embrechts 等。
综上所述,资产间边的权重可表示如下:

(1)
于是便可得到四种相依网络,即皮尔逊相依网络、Kendall’s tau相依网络、斯皮尔曼相依网络和尾部相依网络。
互联矩阵与经典的相关关系矩阵的不同点在于,其中的元素不再仅仅刻画资产间的相依关系,而是从整个网络系统的角度刻画资产间的联结性程度。互联矩阵的详细构造步骤如下所示:
(i)对于某一相依网络,给定一个门限值∈[-1,1],则可构建邻接矩阵,其中元素为:

(2)

(iii)基于每个节点的平均聚类系数,可以得到互联矩阵,其中元素如下:
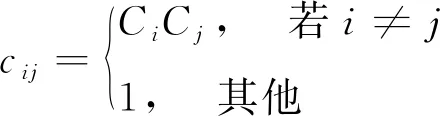
(3)
互联矩阵中的元素由平均聚类系数计算而来,平均聚类系数反映了节点与系统中其他节点的联结程度,因此互联矩阵能够从系统层面量化节点的风险。
(二)优化模型的构建
本文将分别选择最大化夏普比率和最大化风险两种优化准则、方差协方差矩阵及互联矩阵两种资产间关系度量工具,来构建投资组合模型。
基于方差协方差矩阵和最大化夏普比率准则的投资组合模型为:

s.t. 1′=1
(4)
≥0, (=1,2,…,)
基于方差协方差矩阵和最小化风险准则的投资组合模型为:
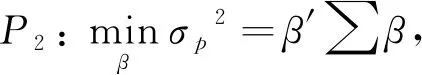
s.t. 1′=1
(5)
≥0, (=1,2,…,)
基于网络结构和最大化夏普比率准则的投资组合优化问题:
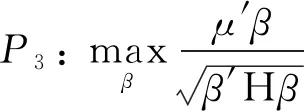
s.t. 1′=1
(6)
≥0, (=1,2,…,)
基于网络结构和最小化风险准则的投资组合优化问题:
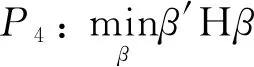
s.t. 1′=1
(7)
≥0, (=1,2,…,)
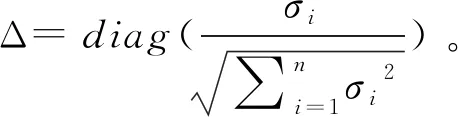
全局最小化风险优化准则是一种较为保守的优化准则,因为在优化过程中只考虑最小化风险而不考虑投资组合的收益见Bodnar等。Clemente等研究的是优化问题,即在全局最小化风险准则下,基于资产网络构建矩阵H用于捕捉风险信息,从而构造优化问题。是本文重点关注模型,优化模型、和作为对比模型出现,其中及的构建见Bodnar等和Sharpe。
三、实证研究
(一)数据选取
通过Joinquant数据平台,获取2012年1月4日—2018年12月28日期间,一直存在于上证50指数及上证基金指数中的47支成分股的日数据。经过计算,最终得到1 700条日对数收益率数据。
(二)优化步骤
本文基于滚窗法探讨不同优化问题的解的表现,具体步骤如下:
步骤一:首先确定长度为的内样本窗宽和长度为的外样本窗宽。
步骤二:运用第一内样本窗口的数据(从=1到=),基于优化问题、及分别四种相依网络下的优化问题和,使用Matlab中非线性优化求解器fmincon进行优化,分别求得10个最优权重。
步骤三:在第一外样本窗口时段中(从=+1到=+)按上一步得到的最优权重投资,记录相关外样本表现。
步骤四:以步长向前滚动窗口,重复上述过程直到达到数据集的末尾。
(三)优化结果
为了计算的便利性及结果的一般性,本文设定外样本窗宽为一个季度,内样本窗宽设定为一年和两年分别进行优化。
1
在内样本中,主要关注最优投资权重的投资结构表现。当窗宽为一年时,最后一个内样本窗口下,47支资产的皮尔逊相依网络、Kendall’s tau相依网络、斯皮尔曼相依网络和尾部相依网络见图1。
由图1可以观察到,在最后一个内样本窗口的任一相依网络中,与其他节点联结程度较强的节点,一般具有较小的方差。
在最后一个内样本窗口下,基于和四种网络下的优化结果绘制于图2。
图2中节点的大小与投资权重成比例。由图2中(a)~(e)可以发现,在任一模型下,最优投资权重都集中在两个资产上,原因在于这两个资产在样本期间具有显著优于其他资产的夏普比率(大部分资产的夏普比率非常小或为负值),且两者的夏普比率大小十分接近。由图2(b),可以看到在(皮尔逊相依网络)下的投资权重更多地分配给右上角资产,从图1(a)中可以发现该资产与其他资产的联结程度相较左下角资产略弱,因此(皮尔逊相依网络)给出的最优投资权重将网络拓扑结构中的联结程度纳入考量,从整个网络系统的角度调整优化了投资组合。对于其他相依网络下基于的最优投资权重,投资结构与图2(b)相似,可以得到上述相同结论。对比图2中(b)~(e),所投资的资产都位于网络外围,但具体权重分配有一定差异,表明不同网络刻画风险的不同侧面,对投资优化结果有一定影响,风险网络的选择取决于投资者的风险偏好及市场环境。
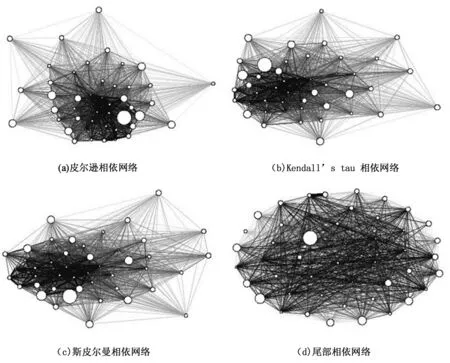
图1 47支资产在最后一个内样本窗口下的四类相依网络注:图中节点代表47支资产,边表示资产间的相关关系(基于不同相关系数进行估计)。节点的大小与资产的方差成比例,边的粗细与相关关系大小成比例。颜色较深区域为网络中心,该区域资产与其他资产联结程度较强,具有较强的风险传播能力。
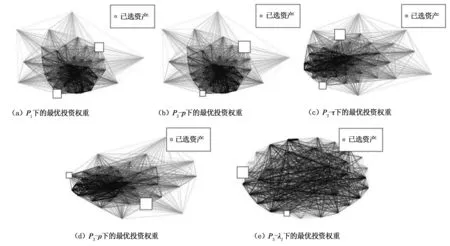
图2 最大夏普比率准则下的最优投资权重
在最后一个内样本窗口下,基于和四种网络下的优化结果绘制于图3。由图3(a)可以发现,经典的全局最小化风险模型的优化结果大体上投资于较外围的资产,这与Pozzi等提出的投资于网络外围资产能够较好地降低投资组合风险相吻合。而图3(b)基于网络方法下的全局最小化风险模型并没有避开投资于网络中心资产,我们分析其原因在于,由图1可知本组数据中各资产的方差差异非常大,资产方差构成了矩阵H的对角线元素,而由本组资产的平均聚类系数计算得到非对角线元素波动较小,因此在优化过程中,对角线元素对优化结果影响较大。而位于网络中心的资产具有相当小的方差,故最终优化结果中较大的投资比例分配于网络中心资产。当基于调整不同相依网络时,我们得到相似的投资网络结构分布,故可得到上述相同结论。但不同网络下,投资的权重分配有一定差异,表明在最小化风险准则下,不同风险网络的选用对投资优化结果有一定影响,这与Clemente等中结论一致。
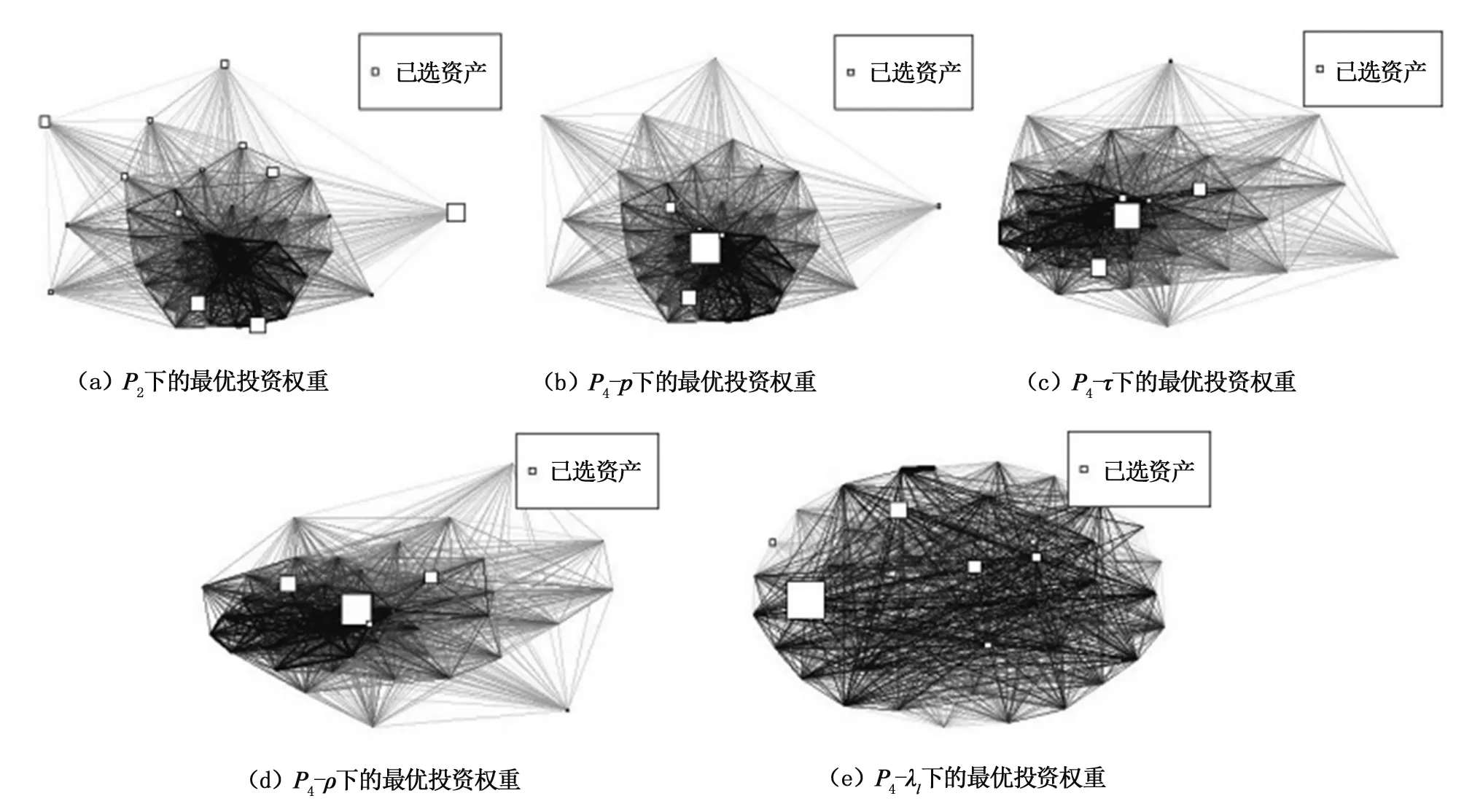
图3 全局最小化风险准则下的最优投资权重
对比图2与图3可知,基于最大化夏普比率准则优化得到的投资组合更加稀疏,即其较为集中地投资于少数资产,策略相对较为激进。且可以发现基于最大化夏普比率准则的最优投资组合更好地避免了投资于网络中心的资产。我们分析其原因在于本文数据的最后一个样本窗口中,当考虑全局最小化风险准则时,个体维度信息(资产自身方差)在不同资产间波动较大,对于优化结果起到了主导作用。而当考虑最大化夏普比率时,个体维度信息(资产夏普比率)在不同资产间波动较小,网络联结性信息对优化结果产生作用。因此表明基于网络的投资组合方法对数据集的特点具有一定的要求,当数据集的个体维信息扩散程度较小,而网络依赖关系扩散程度较大时,基于网络的投资组合方法可能会更加适用。
当窗宽为两年或选取不同样本窗口时,可以得到相似结论,故不再进一步展示结果。
2

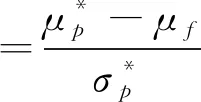
(8)
其中,代表无风险资产收益率,为了计算方便,此处设置=0。
Omega比率由于没有任何分布假设,且不局限于收益率分布的一阶矩、二阶矩信息,Omega比率因此能够更好反映投资组合的表现。
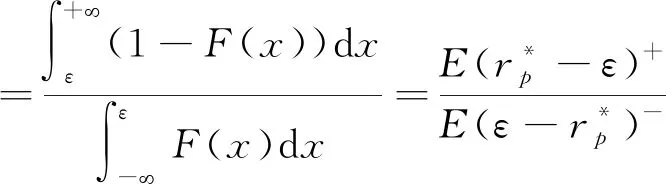
(9)
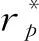
由于DeMiguel等提出大部分已有优化准则无法连续的击败等权投资策略,故我们在接下来的外样本表现评价中同时引入等权投资策略作为对比。
当窗宽为一年时,投资组合的外样本表现如表1所示。
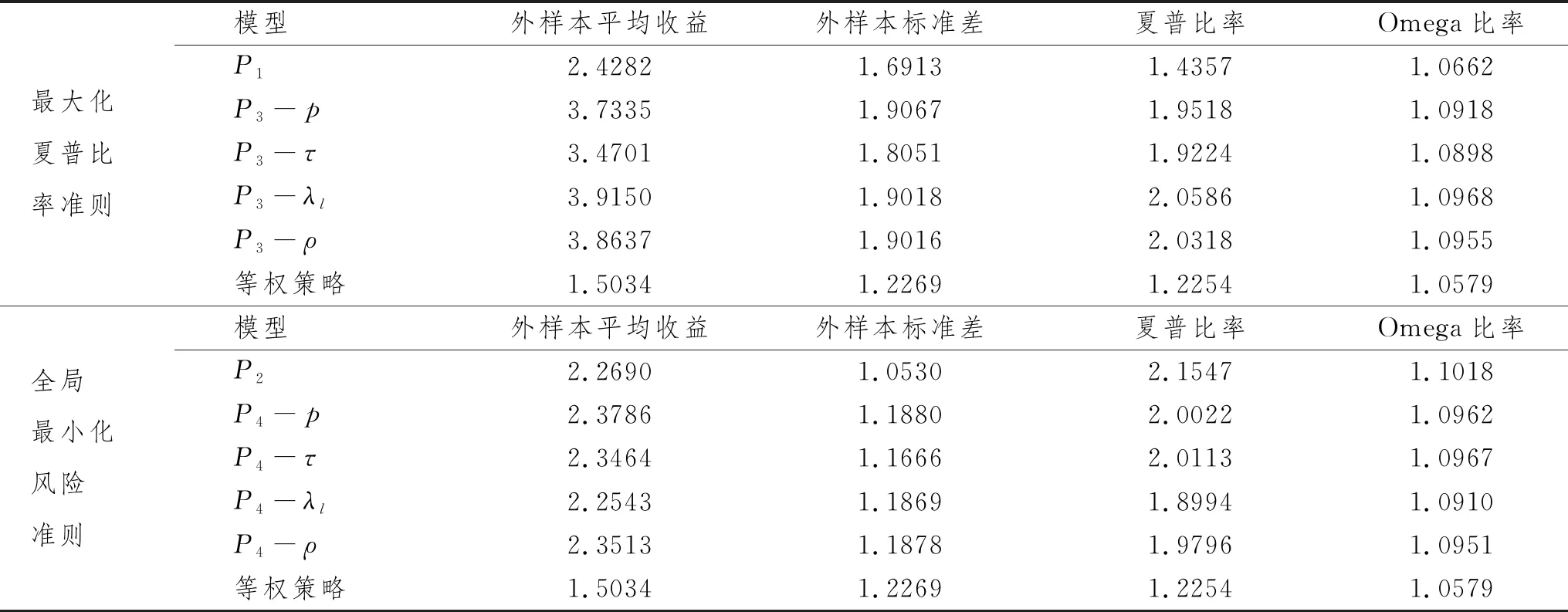
表1 不同优化准则下基于各模型的外样本表现(窗宽为一年)
由表1我们可以发现:在全局最小化风险准则下,基于样本方差-协方差矩阵的传统模型()优化得到的投资组合具有最高的夏普比率及Omega比率,外样本表现最佳。即传统模型()具有优于Clemente等中模型()的表现,但在Clemente等中数据背景下,具有良好的表现。这说明在将网络风险传染性纳入考量的过程中,的表现受到市场环境的影响。
而在最大化夏普比率准则下,基于尾部相依网络的模型(-)优化出的投资组合外样本表现最佳,具有最高的夏普比率及Omega比率,表明在当前数据及优化场景下,尾部相依网络所捕捉的网络结构更加适用,且将网络风险传染性纳入考量的模型具有更优的表现。
对比两种不同的准则,可以发现在最大化夏普比率准则下, 最优投资组合具有较高的外样本平均收益,但同时具有较大的外样本标准差,故而具有较小的夏普比率及Omega比率。这意味着基于最大化夏普比率准则,往往得到更加激进的投资策略,即既具有更大的收益但需承担更大的收益波动风险。因此,最大化夏普比率准则在熊市下应谨慎选择。
当窗宽为两年时,投资组合的外样本表现如表2所示。

表2 不同优化准则下基于各模型的外样本表现(窗宽为两年)

续表2
由表2我们可以发现:在全局最小化风险准则和最大化夏普比率准则下,基于样本方差-协方差矩阵的模型(和)优化出的投资组合外样本表现最佳,具有最高的夏普比率及Omega比率。这说明了本文参照Clemente等通过构建矩阵H将网络风险传染性纳入优化模型的方法,具有一定局限性。基于该方法下,考虑不同投资准则得到的最优投资组合并不具备稳定的优于传统模型结果的能力。市场环境及窗宽的选取都对该方法应用于优化模型有一定的影响。
对比两种不同的准则,可以发现在最小化风险准则下,投资组合的表现更优。这意味着即使变换窗宽,即考虑长线投资,基于最小化风险准则,依旧得到更加保守的投资策略。因此,不同窗宽的选取,对于最小化风险准则和最大化夏普比率在策略保守程度的影响不大。
四、结论与建议
(一)研究结论
本文在基于网络方法的投资组合优化模型中,考虑了最大化夏普比率准则,构造了多种投资组合优化问题,运用滚窗法探讨动态调整的最优投资策略。
实证研究选取2012年1月4日—2018年12月28日样本期间内一直存在于上证50指数及上证基金指数中的47支成分股数据,分别在最大化夏普比率准则和全局最小化风险准则下,基于经典的方差-协方差矩阵及四种不同相依网络,构建了10个优化问题进行投资组合优化。在优化过程中本文选用滚窗法,并分别选取内样本窗宽为1年和2年。
研究结果发现:
第一,与全局最小化风险准则相比,基于最大化夏普比率准则的模型会产生更积极的策略,其可能更适用于风险偏好投资者;
第二,Clemente等提出的网络方法需要在特定市场环境及窗宽下才能具有较优的表现,说明该方法具有一定的局限性,如何更好地将网络中的结构性风险引入投资优化模型有待进一步研究;
第三,在本文数据集下,基于网络方法的最优投资组合在最大化夏普比率准则下能够更好规避投资于网络中心资产;
第四,不同的相依网络对于优化结果的结构影响较小,对于个别资产的具体投资权重及投资组合的外样本投资表现有一定影响,说明投资者在应用本文模型时应灵活选取相依网络以适配不同的投资环境及风险侧重。
(二)政策建议
第一,投资机构及个人提高对于金融网络中资产风险传播能力的认识。在收益率及波动性间进行权衡的传统投资决策思路应进一步拓宽。金融资产在整个金融系统中的重要性程度,风险传播能力对于投资策略的表现有着不可忽略的影响。尤其面对当今极端风险频发的市场环境,应考量策略中资产间的风险传染关系,避免投资组合遭遇巨大损失。
第二,金融投资部门加强金融网络中资产风险性质在投资决策中应用的研究。现有文献中,将网络中资产的风险传染特性等相关拓扑性质引入投资决策的研究尚待进一步完善。应通过更优的投资优化模型,为投资机构及个人提供个性化的投资优化方法建议,以推进投资决策方法的良性发展。
第三,推进资本市场开放。我国股市起步较晚,股价同步性程度较高,金融网络中资产间的风险传染性较强,一旦遭遇极端风险,风险将快速在金融网络中蔓延。可逐步增强我国资本市场对外开放程度,继续拓宽资本市场的互联互通渠道,例如,开展“沪伦通”等开放政策,增强我国资本市场的活力及韧性,降低风险在金融网络中的传染速度。

