基于改进鲸鱼算法的微电网系统容量优化研究

郝晓弘，王 锐，裴婷婷，黄 伟

（兰州理工大学 电气工程与信息工程学院，兰州730050）

由于能源短缺、环境污染问题的日益突出，人们对以风电、光电为代表的可再生能源发电技术的研究利用逐渐深入。在多能源联合发电系统容量配置问题中，国内外的学者对其进行广泛的研究，并取得一定研究成果。文献[1]在光储独立微电网系统中，对储能设备的运行特性加以考虑后，研究了微电网中储能的容量优化配置方法，但是研究中未能考虑风力的输出功率；文献[2]通过对不同风光储容量配比方案的对比，给出最优方案，但是该方案仅限于白天供电，不能满足全天的用电需求；文献[3]认为风力发电与光伏发电具有良好的负相关特性，并利用这种特性开展以成本最低和负荷失电率最低为目标的容量优化，但未对储能蓄电池的使用寿命加以考虑；文献[4]研究了风电-光伏-蓄电池联合系统，但由于蓄电池具有生命周期短、价格昂贵等特点，增加了系统投资及运营成本；文献[5]利用电加热器实现风电-光热联合运行，但光热电站的发展很大程度上受限于经济，其投资成本的50%在集热场。

以上研究均采用单一储能作为平抑风力发电、光伏发电的方式，但是单一储能很难同时满足频繁充放电和大量储存电量的要求，考虑到投资成本问题，不利于实现收益最大化。因此，本文通过研究风力发电、光伏发电在空间以及时间上的互补性，建立了储能容量最小、运营成本最低的的微电网优化配置模型，充分考虑蓄电池、氢储能混合储能系统的影响因素及运行原则，应用改进型鲸鱼算法，得到储能容量最小、运营成本最低的多目标优化方案，并对所提方法进行验证。

1 风光储联合发电系统

1.1 风光储联合发电系统组成

风光储联合发电系统的构成主要包括风力发电、光伏发电、蓄电池、氢储能、微电网能量管理系统、逆变器、负载等部分组成，其结构如图1所示。

1.2 风机发电模型

风力发电机（wind turbine，WT）输出功率受到多重因素影响，与风速之间近似关系[6]可表示为

式中：Pr为额定功率；v为实际风速；vci为切入风速；vco为切出风速；vr为额定风速。

1.3 光电模型

光伏发电受光照辐射、温度等气象条件影响，其出力模型可表示为[7]

式中：SPV为光伏面板所接受光照辐射面积；L（t）为光照辐射数值；φPV（t）为能量转换效率；φinv为逆变器转换效率，光伏组件的能量转换效率与温度二者间关系为

式中：ηref为组件在标准温度下参考能量转换效率；β为能量转换效率受温度的影响系数；TC（t）为t时刻组件的实测温度；TCref为组件参考温度。光伏组件温度变化受太阳辐射、环境温度共同影响，其作用关系为

式中：Tambient为周围实时环境温度；Trated为光伏组件运行的标准温度。

1.4 蓄电池充放电模型

综合考虑蓄电池自身容量规模、充放电效率、放电深度等特性，对蓄电池建模，其出力模型为

系统充电：

系统放电：

式中：SOC（t）为t时刻结束蓄电池剩余电量；σ 为每小时蓄电池自放电率；Δt为t时间段长度；Pc，Pd分别为蓄电池第t时间段的充电、放电功率；ηc，ηd分别为蓄电池充电、放电效率；Emax为蓄电池的最大容量。

1.5 氢储能系统模型

在微电网系统中，氢储能系统（hydrogen energy storage system，HESS）是储能系统的重要构成部分，HESS 主要由燃料电池（fuel cell，FC）、电解槽（electrolyzer，El）和氢气罐（hydrogen tank，HT）组成。

1.5.1 燃料电池数学模型

燃料电池的简化数学模型为[8]

式中：Qb为燃料电池的耗氢量；Nstack为电堆串联个数；Ib为燃料电池的输出电流；Pb为燃料电池的输出功率；Ub为电堆电压。

1.5.2 电解槽数学模型

碱式电解槽的氢气生产率为[9]

式中：nH2为电解制氢产的摩尔数；ηF为法拉第效率；I为电解电流；Nc为电解槽个数；F为法拉第常数。

1.5.3 氢气罐数学模型

假定储气罐是一个无损封闭系统，按照克拉伯龙方程，储氢装置的数学模型为

式中：Q（t0+Δt）为t0+Δt时刻的氢气体积；q（t）为储氢速率；Q（t0）为t0时刻氢气的体积；p（t）为t时刻储氢罐的压力值；QsN为储氢罐的总体积；n（t） 为t时刻氢气的摩尔量；R为气体常量；T为气体热力学温度。

2 容量优化配置模型

本文在考虑独立型微电网经济性的同时，也需要考虑其供电的稳定性，因此将两者统一量纲，建立储能容量最小、运营成本最低的优化配置模型。

2.1 目标函数

所提风光储微电网优化配置目标函数为考虑微电网投资成本系统运行约束条件下的系统综合运行费用ftotal最小。目标函数1 可表示如下：

式中：Cinv，Com，Cbs分别表示为微电网的初始投资、运维成本以及售电收益。

微电网初始投资可表示为

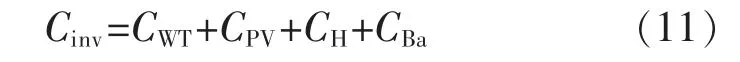
式中：CWT为风电投资成本；CPV为光电投资成本；CH为氢储能投资成本；CBa为蓄电池投资成本。

运维成本可表示为

式中：CoWT，CoPV，CoH，CoBa分别表示为风电、光电、氢储能、蓄电池的运维成本。

售电收益可表示为

式中：CSell表示为售电价格；Psell（t）为t时刻售电功率；Δt为时间段。

目标函数2 为搭建多能源的微电网优化配置模型，包含风电、光电以及氢储能蓄电池组成的混合储能系统，可表示为

式中：EHess定义微电网系统所需配置的储能容量；T为微电网年运行时间；Hess_c（t）是t时刻系统不考虑储能设备荷电状态限制时所需的储能容量；minHess_c（t）为t+Δt时刻之后各电源端与混合储能系统之间最小差值。

式中：ηin为充电效率；ηout为放电效率；Δp为每小时功率失配，其表达式如下：

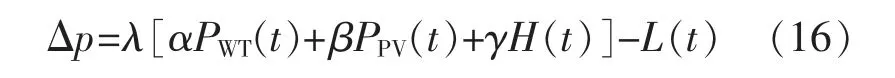
式中：λ 为微电网中风、光、燃料电池发电能源相对负荷的比例；α 对应于风电出力占比；β，γ 则分别对应于光伏与燃料电池的出力占比，且α+β+γ=1；L（t）为1 h 负荷功率；PWT（t）表示微网中光伏每小时出力；PPV（t），H（t）则分别为每小时风电与氢储能的出力。

2.2 约束条件

（1）系统容量约束

微电网中的风、光、燃料电池同时供电时，各自的装机容量所占比例需要小于1 大于0，且总和为1。

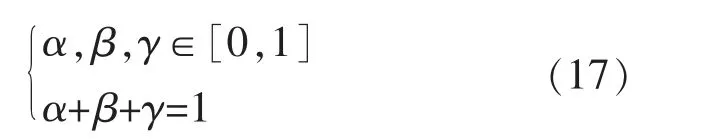
（2）系统功率平衡约束

式中：PWT（t）为第t时段内风力发电机的出力；PPV（t）为第t时段内光伏电池出力；Pd（t），PH（t）分别为混合储能中的蓄电池、氢储能的出力。

（3）HESS 的SOC 约束

以荷电状态（state of charge，SOC）定义混合储能系统的剩余容量，即混合储能系统的剩余容量比额定容量。

式中：SOCmax，SOCmin，EHess，Hess_c（t）分别是储能系统中的运行荷电状态的上限约束、下限约束、运行荷电状态的上限约束、储能系统中的额定容量、实际存储容量，SOCmin，SOCmax的取值范围为［0，1］。

3 改进鲸鱼算法求解

3.1 鲸鱼算法

在2016年，澳大利亚学者提出的新型群智能算法——鲸鱼优化算法（whale optimization algorithm，WOA）[10]。WOA 是根据模仿座头鲸包围、涉猎、搜索猎物[11]3 种行为建立的数学模型。WOA 具有参数调整少、操作简单且跳出局部最优能力强的优点[12]。

第1 阶段：包围阶段数学模型为

式中：D 为当前求出的最优解与搜索体的距离向量；t为当前迭代次数；X*为当前最优解的位置向量；X 为搜索体的位置向量。

第2 阶段：

第3 阶段：

式中：Xrand表示当前种群中随机一个搜索体所在的位置[13]。

3.2 改进鲸鱼算法

针对WOA 所出现的问题，动态搜索和协同进化的鲸鱼优化算法（dynamic search and cooperative learning for whale optimization algorithm，DCWOA）通过对种群个体进行分工、调整搜索策略等措施加以改进，并与WOA 在多目标优化求解中进行对比分析。

种群个体分工主要包括精英个体指导进化、变异策略跳出局部最优两个方面：

（1）种群内的精英个体，以式（26）取代WOA 中的式（21）和式（22），更新下次迭代的位置信息，以达到加快算法寻优速度的目的。

式中：X*（t）和X*（t-1）为相邻两次更新的全局最优值（X*（t）和X*（t）不相等）；区间［1，5］为α 的随机数，以保证其能得到延长线上的某一点。

（2）在迭代后期，针对陷入局部最优难以跳出的问题，本文通过变异策略，以式（27）进行高斯变异或柯西变异，来跳出当前的搜索范围，以此跳出局部最优。

式中：r为［0，1］的随机数；X*为当前全局最优位置；X（t）为个体第t次迭代时的位置信息；G（0，1）为标准高斯分布；C（0，1）为柯西分布。

动态调整搜索策略主要在调整收敛因子、调整搜索方程两个方面进行：

（1）在调整收敛因子方面

由式（20）可知，收敛因子a对参数C的值影响程度较大，通过式（28）动态调整收敛因子a，对算法的搜素能力进行平衡，以提高算法整体寻优性能。

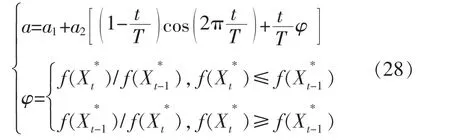
式中：a1，a2分为调整参数A的常量；T为最大迭代次数；为第t次迭代时种群内存储的当前全局最优值；为t-1 次迭代时的当前全局最优值；φ 为相邻两次迭代过程中的全局最优值之比，φ∈［0，1］。

（2）在调整搜索方程方面

在迭代运算的后期，种群内个体成汇聚状态，这种状态将会严重影响算法的搜索能力。为了减少汇聚状态对算法搜索能力的干扰，通过式（29）对其调整，以此提高全局搜索能力。

3.3 求解步骤

在求解“风光氢蓄”微电网的最优容量配比问题中，本文应用DCWOA 求解，流程如图2所示。

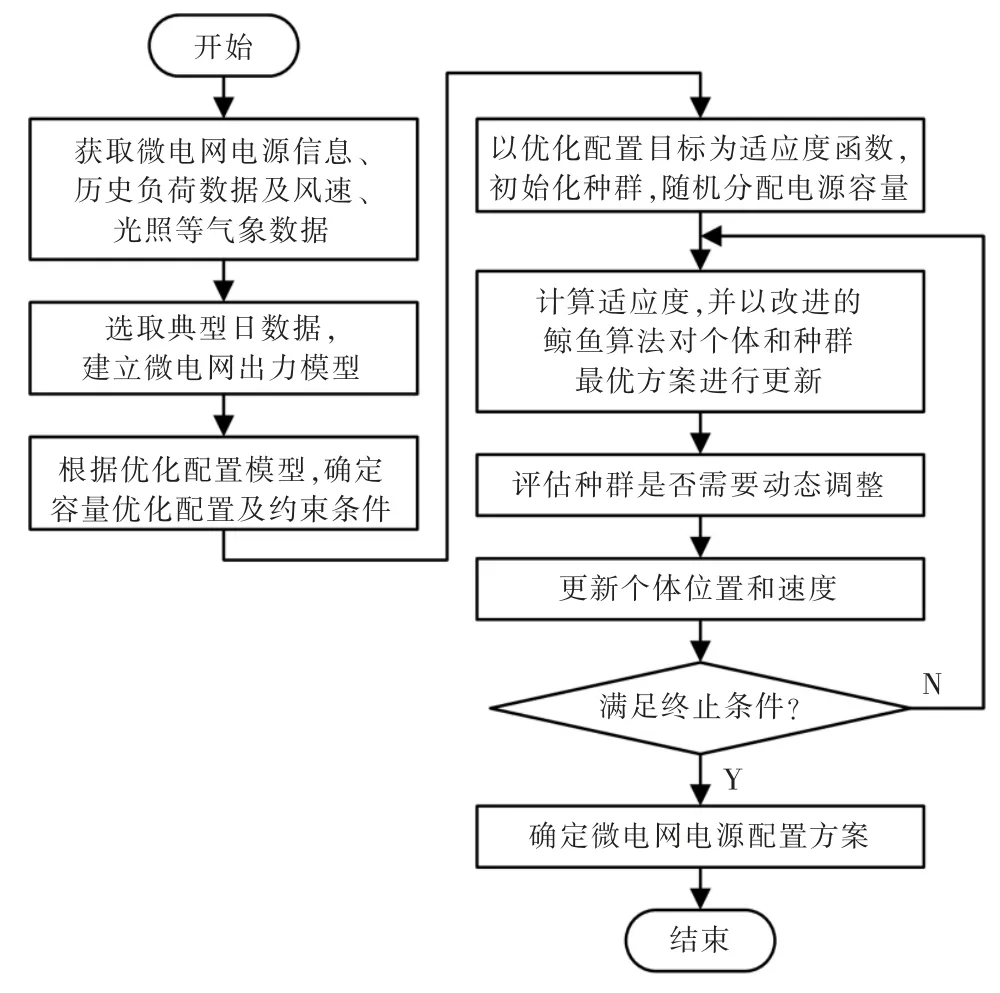
图2 求解流程Fig.2 Solution flow chart of model

4 仿真结果分析

4.1 仿真介绍

微电网系统容量优化应用DCWOA 进行求解，其优化的决策变量是风力发电机、光伏电池、氢储能、蓄电池组的数目，故该问题的［NWTNPVNHNBa］对应算法种群个体，各个组件参数如表1所示。以某地区的风光资源、负荷功率为例，选择一个自然年的春分、夏至、秋分以及冬至作为典型月的典型日进行分析，微电网系统的风光出力曲线及负荷功率曲线如图3所示。

图3 典型日发电功率及负荷曲线Fig.3 Typical daily power generation and load curve

表1 设置系统仿真参数Tab.1 Set system simulation parameters

4.2 优化结果分析

风光储优化结果如表2所示。

表2 优化结果Tab.2 Optimization results

由表2 可知，在微电网容量最优配置下，风力发电容量为249.6 kW，光伏电池装机容量为212.8 kW，氢储能容量为129 kW，蓄电池容量为91.2 kW，此时实际综合成本费用最小为209.33 万元。风力发电容量比光伏发电容量偏大一些，原因是所研究地区风力资源丰富，可使风机白天夜间均能发电。若增大光伏的发电容量，同时会增大氢储能蓄电池储能系统的容量，间接增加投资成本，不利于实现运营收益最大化。

相较于风光互补发电，氢储能在发电成本上占据很大优势，并且氢储能在各个时刻可以在零到额定功率下工作，但受成本制约，氢储能、蓄电池容量配置也会受到一定限制。

由图4 对比分析，可以看出，利用动态搜索和协同进化的DCWOA 能够使得DCWOA 算法有效地获得更好的Pareto 解集。二者迭代多次以后，有了明显的差别，DCWOA 在收敛速度以及收敛精度明显要优于WOA，且DCWOA 改善了WOA 在迭代运算中易出现的搜索速度慢、寻优精度低以及易陷入局部收敛等问题。

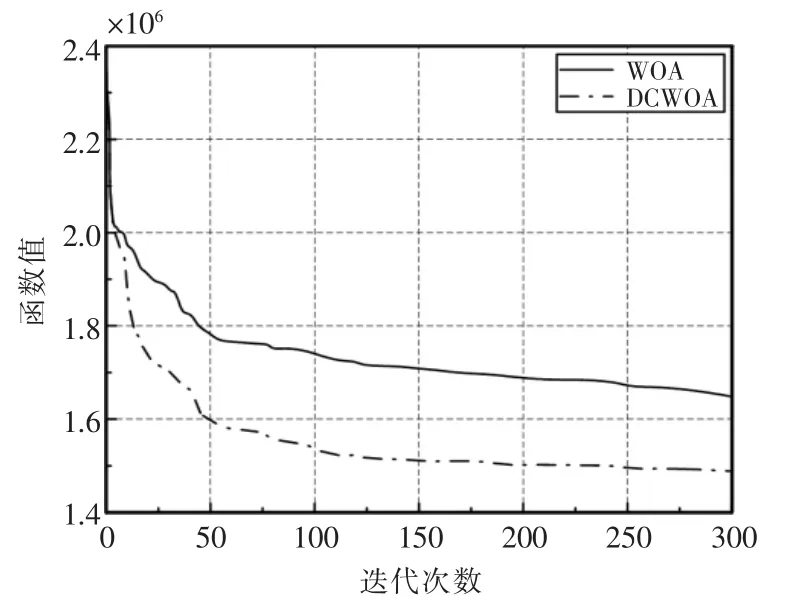
图4 迭代曲线Fig.4 Iteration curve

5 结语

本文通过充分考虑蓄电池、氢储能混合储能系统的影响因素及运行原则，建立了微电网优化模型，在此基础上，应用改进型鲸鱼算法，得到储能容量最小、运营成本最低的多目标优化方案并得出结论：不同季节的天气状况会对电源的容量配置、系统总成本及储能系统的充放电次数有影响；当风机光伏发电容量配备比例约为1∶1.17，氢储能及蓄电池组比例约为1∶1.4 时，系统成本最低，且充分提高供电可靠性；DCWOA 在迭代运算中的搜索速度与寻优精度都有了一定的提高，与此同时易陷入局部最优的问题也得到了很好的解决。

在搭建系统容量优化配置模型时，经济性指标并未考虑电网对风光蓄氢多能源系统的功率缺额惩罚及副产品氧气的经济价值，将作为后续研究内容。