减载运行双馈风力发电机参与系统调频的多风速段变系数控制策略

周仙丰，王娟娟

（大连交通大学 自动化与电气工程学院，大连116028）

双馈风力发电机（doubly-fed induction generator，DFIG）的转子与电网通过功率变换器相连，转子转速与系统频率完全解耦，无法响应系统频率变化，不利于系统频率的稳定。因此，风电机需要具备类似同步发电机一样的调频能力[1]。目前风电机参与系统调频的主要控制方式分为转子动能控制和减载控制，其中转子动能控制包括下垂控制和虚拟惯性控制，减载控制包括转子超速控制和变桨距角控制[2]。对于最大功率运行状态的风机，转子转速的增大或减小都能降低风机出力，但减速运行的风机不利于系统稳定，所以一般采用转子超速控制实现减载[3]。文献[4]分析了转子超速控制的减载能力，指出其适用范围受风机最大转速限制；文献[5]采用变桨距角控制，通过增大桨距角实现风机的减载运行；文献[6]将转子超速控制和变桨距角控制结合使用，对于不同的风速采用不同的控制方法，充分利用转子超速和变桨距角控制的优势。

针对DFIG 减小系统惯量的问题，文献[7]提出虚拟惯性的概念，通过在DFIG 功率控制回路中附加虚拟惯性控制环节响应系统频率变化，使风机释放或吸收转子动能参与系统调频；文献[8]将下垂控制和虚拟惯性控制结合进行调频，但调频结束后转子恢复原转速吸收有功，易造成频率二次跌落；文献[9]采用固定的下垂系数进行频率调节，但由于风机的出力和风速有关，固定参数的下垂控制不能充分利用风机的备用容量参与系统调频；文献[10]提出变下垂控制策略，利用优化后的下垂系数对风电机组进行设定，以此改善其调频效果，但并未给出桨距角的计算方法。

本文将转子超速控制和变桨距角控制相结合，考虑到风能利用系数和叶尖速比与桨距角间复杂的非线性关系，定义减载程度，通过数值计算的方法将转速、桨距角、机械功率和减载程度间的对应数值求解出来。然后考虑不同风速下双馈风机能达到固定减载程度所采用的控制方式对风速进行分段，并对下垂系数和惯性系数进行整定，提出双馈风机参与系统频率调节的控制策略，并通过仿真验证了控制策略的有效性。

1 DFIG 减载运行控制策略

1.1 转子超速和变桨距角控制原理

双馈风机的风轮输出机械功率表达式为

式中：ωm为风轮机械角速度；R为风轮半径；V为风速；λ 为叶尖速比；β 为桨距角；Cp为风能利用系数；ρ 为空气密度；Pm为风轮机械功率。

根据式（1）可知风机的输出功率主要与风速、风轮转速和桨距角有关，在某一风速Vw0下风轮输出的机械功率与转速及桨距角的关系曲线如图1所示。

图1 风轮输出机械功率与转速和桨距角的关系曲线Fig.1 Relationship curve between wind turbine output mechanical power and speed and pitch angle

由图1 可知，当双馈风机运行于最大功率输出模式，即图中MPPT 曲线时，增大转子转速或桨距角都会使风机输出功率下降，从而实现减载运行。

1.2 转子超速和变桨距角控制策略

定义减载程度d%，其表示在任意风速条件下，通过转子超速和变桨距角控制使风机发出当前风速下（1-d%）的最大输出功率。风轮输出机械功率与转速和风速的关系曲线如图2所示，其中ωmax为风机最大转速；Pmax为风机最大功率；Vw，cut-in为风机最小切入风速，Vω2＞Vω1＞Vω，cut-in；βmin为最小桨距角；ABCD为风机以最大功率跟踪方式运行的功率曲线；A′B′C′D′为风机按d%减载运行的功率曲线。

图2 风轮输出机械功率与转速和风速的关系曲线Fig.2 Relationship curve between mechanical power output of wind turbine and speed and wind speed

由图2 可知，风速Vw1为风机仅通过转子超速控制实现d%减载的风速上限，其控制区域为A′B′BA。风速Vω2为使用转子超速控制方式的最大风速，此时需要结合转子超速控制和桨距角控制才能实现d%减载，该模式的控制可行区域是BB′C。风速大于Vω2时，如图2 中CD区域所示，此时受到风机转子最大转速的限制，只能采用变桨距角控制。

本文以2.4 MW 双馈风力发电机为例，风机的基本参数见表2～表5，结合式（1）便可得到该风机按最大功率模式运行下的风速—转速和风速—功率特性曲线，如图3所示。

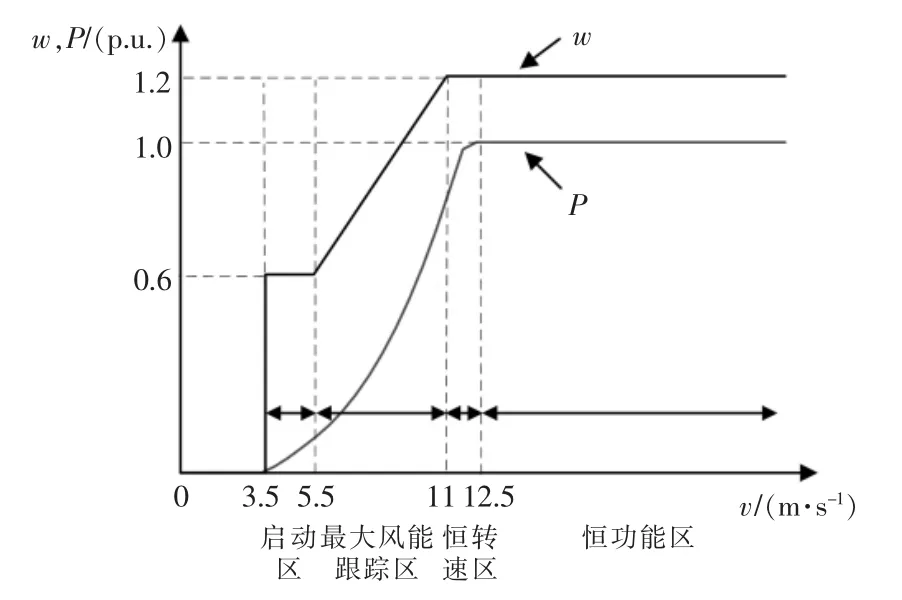
图3 2.4 MW 双馈风机转子转速和输出功率特性曲线Fig.3 Rotor speed and output power characteristic curve of 2.4 MW doubly fed fan

由式（1）可知当风速一定时，输出功率Pm主要与风机转速ω 和桨距角β 有关，但Pm，ω 和β 间具有严重的非线性关系，因此本文采用数值计算的方法对其求解，计算流程如图4所示。

图4 转速、桨距角数值计算流程Fig.4 Numerical calculation flow chart of speed and pitch angle

机械功率误差ε 与转速间隔a及桨距角间隔b的取值有关，a和b越小，功率误差ε 取值越小，计算结果越精确。

2 减载风电机组一次调频策略

2.1 下垂控制和惯性控制原理

DFIG 的转子通过功率变换器接入电网，转子转速和系统频率解耦，使其不具有调频能力，为了使DFIG 能够响应系统频率的变化，在DFIG 的有功控制环节加入下垂控制和虚拟惯性控制来响应系统频率的变化，其基本原理如图5所示。

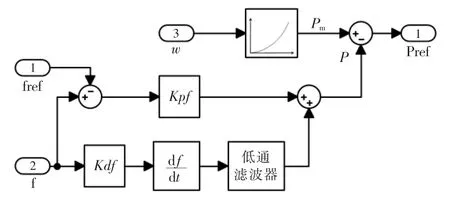
图5 下垂控制和虚拟惯性控制原理图Fig.5 Schematic diagram of droop control and virtual inertial control

2.2 下垂控制系数整定

对于同步发电机，其下垂特性为

式中：KG为同步发电机的单位调节功率；为单位调节功率的标幺值；PGN为同步发电机额定功率；fN为系统额定频率50 Hz；δG为调差系数。

模拟同步发电机的双馈风机下垂特性为

式中：Kpf为DFIG 的单位调节功率；为单位调机功率的标幺值；PWN为DFIG 的额定功率；δw为DFIG调差系数。

根据同步发电机的调差系数来定义DFIG 的调差系数δw为

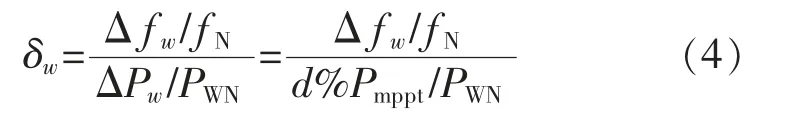
式中：Pmppt为当前风速下DFIG 所能发出的最大功率，Δfw为系统频率偏差。

综上可得DFIG 的下垂控制系数的计算公式为

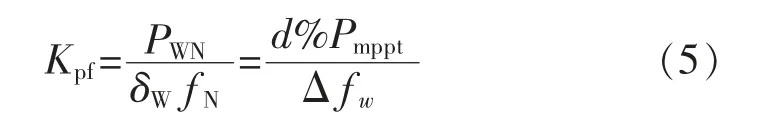
2.3 惯性控制系数整定

同步发电机转子机械角速度为

DFIG 额定运行状态下转子所储存的动能为

由于DFIG 额定运行状态下转子的电角速度和同步发电机的电角速度不相等，因此需要将DFIG转子储存的动能等值到同步电角速度下，同步电角速度下DFIG 转子储存动能为

联立式（7）和式（8）可得DFIG 等效到同步转速下的转动惯量为

式中：f为系统频率；p为极对数；JDFIG为折算到DFIG 高速轴的等效转动惯量；Jt，a为低速轴转动惯量；Jm为高速轴转动惯量；JN为等值到同步角速度的等效转动惯量；N为齿轮箱变速比；ωwn为DFIG 转子额定机械角速度；ωn为同步角速度。

当DFIG 转速变化时，其转子释放的动能为

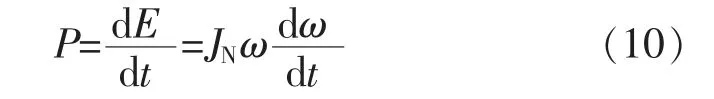
等值发电机组惯性时间常数为

联立式（10）和式（11）可得

用标幺值表示为

由于当ω，f取标幺值时，其值相等，因此式（13）可变为

换算为有名值为

综上惯性控制系数的计算公式为

式中：H为等值发电机的惯性时间常数；SN为DFIG额定容量；PDN为DFIG 额定有功功率；Pdf为惯性控制增发功率；Kdf为惯性控制系数。

2.4 DFIG 调频控制策略

结合上文分析，本文将DFIG 参与系统调频的控制区间按风速区段划分为3 个区域，控制方式如表1所示。

表1 DFIG 调频控制方式Tab.1 DFIG frequency modulation control mode

表1 中Vw，cut-in和Vw，cut-out分别为风机运行的切入风速和切出风速；Vw1为低、中风速的分界，其值为

Vw2为中、高风速的分界，其值由下式计算

式中：ωmax为DFIG 最大转速；Cpmax为最大风能利用系数；λmppt为最优叶尖速比。

对于中风速区DFIG 参与系统调频时，优先采用转子超速控制，当转子超速控制不能满足调频需求时，再采用桨距角控制。

为了便于仿真，本文对下垂系数Kpf和惯性系数Kdf均采用离线方式进行求取。对于下垂系数Kpf，减载率d%取为10%，频率偏差Δfw取0.2 Hz，Pmppt可通过最大功率跟踪模式下的V-Pmppt曲线求得，代入式（1）便可得到V-Kpf特性曲线。对于惯性系数可通过同样的方式求解，由于系统频率偏差通常不会超过0.5 Hz，因此f取值范围为50±0.5 Hz，其它参数见表2～表5所示，计算可得f-Kdf特性曲线。

结合上文分析，DFIG 参与系统频率调节控制策略如图6所示。其中下垂系数Kpf和惯性系数Kdf均由查表所得，最大转速变化率、最大功率调节速率和最大桨距角变化率的取值分别为0.5p.u./s，0.3p.u./s 和10°/s，调频死区为50±0.2 Hz，减载率d%为

图6 DFIG 调频控制框图Fig.6 DFIG FM control block diagram

式中：Pmppt为当前风速下DFIG 能发出的最大功率；P为DFIG 实际输出功率；ΔP为需求的调频功率；Pref为DFIG 应发功率。通过查表可得转子转速的理论值，桨距角理论值同理。Vw2为惯性控制选择模块，当风速大于Vw2时，转子转速固定为最优转速，惯性控制输出功率为0。为当前转速和滞后转速间的差值，用于判断中风速区是否启动桨距角控制，当大于设定值时，转子转速变化响应系统调频；当小于设定值时，转子转速不变，若此时频率仍超出调频死区便启动桨距角控制进行调频。

3 仿真结果分析

本文利用Matlab/Simulink 搭建了一个由4 台同步发电机、1 台DFIG 和负荷组成的仿真系统。其中同步发电机的额定功率为2 MW 并带有调速器和调频器，不设调频死区。DFIG 的额定容量为2.4 MW，其详细参数如表2～表5所示。

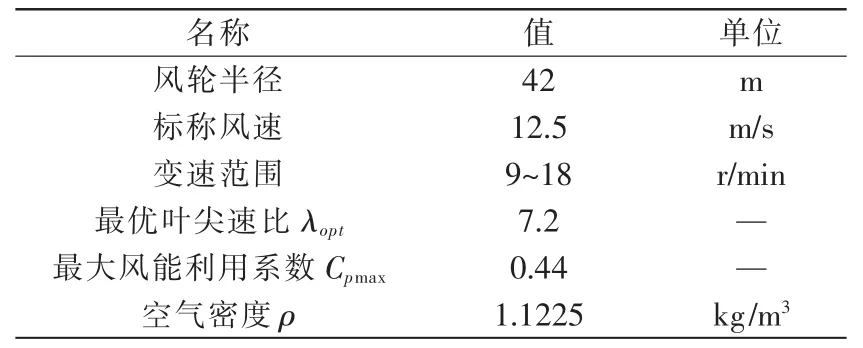
表2 风力机参数Tab.2 Wind turbine parameters

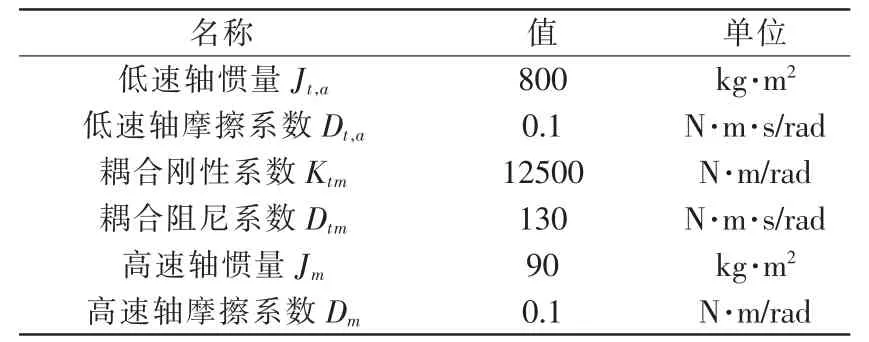
表3 机械系统参数Tab.3 Mechanical system parameters

表4 发电机的主要特性参数Tab.4 Main characteristic parameters of generator

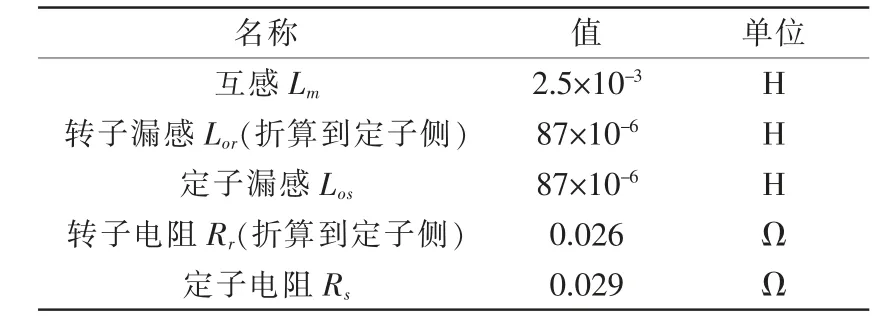
表5 发电机等效电路参数Tab.5 Parameters of generator equivalent circuit

系统初始带4 MW 负荷运行，10 s 时系统负荷增加1.2 MW。考虑不同风速区间DFIG 调频的方式不同，选取3 个具有代表性的风速进行仿真，仿真结果如图7～图9所示。

图7 低风速（8 m/s）仿真结果Fig.7 Simulation results of low wind speed（8 m/s）

图9 高风速（13 m/s）仿真结果Fig.9 Simulation results of high wind speed（13 m/s）

由图7 可知，系统负荷突然增加且频率超出死区频率时，下垂控制和惯性控制同时作用，DFIG 转子转速快速下降，风轮所捕获的机械功率沿减载曲线逐渐上升并释放转子动能，输出电磁功率快速上升对系统有功缺额提供暂态支撑，系统最低点频率相比DFIG 不调频时有较大提升，当转速下降到约0.9 时，此时转速是风速为8 m/s 时的最优转速，不再变化，转子动能释放完毕，不再为系统提供暂态有功支撑，电磁功率迅速下降至DFIG 稳态运行时输出的机械功率值，由于电磁功率的快速下降导致系统频率二次跌落，此时DFIG 已达到当前风速下所能发出的最大功率，随后由同步发电机调频直至系统频率回到稳态。

由图8 可知，系统负荷增加时，系统频率、转子转速和电磁功率变化方式和风速为8 m/s 相同，区别在于风速为10 m/s 时DFIG 的备用功率更多，转子转速更大，因此DFIG 参与调频时增发的机械功率和转子释放动能提供的电磁功率更多，系统最大频率偏差减小，当转子转速达到稳态时，系统频率二次跌落超出调频死区，此时转子转速已达到最优值，风轮桨距角开始减小，风轮捕获的机械功率增加，进一步为系统频率提供支撑。

图8 中风速（10 m/s）仿真结果Fig.8 Simulation results of medium wind speed（10 m/s）

由图9 可知，由于此时转子转速被限制到最大值，不能通过降低转子转速释放动能为系统提供暂态有功支撑，DFIG 只通过改变桨距角从而改变捕获的机械功率来参与系统调频，系统频率最低点下降的最多，但稳态时DFIG 能够提供更多的有功功率，减小了同步发电机的调频压力。

仿真波形的关键数据如表6所示。表中fmin为系统最低点频率；ΔP稳为DFIG 达到稳态时的有功功率变化量；ΔP暂为最大暂态有功功率支撑。

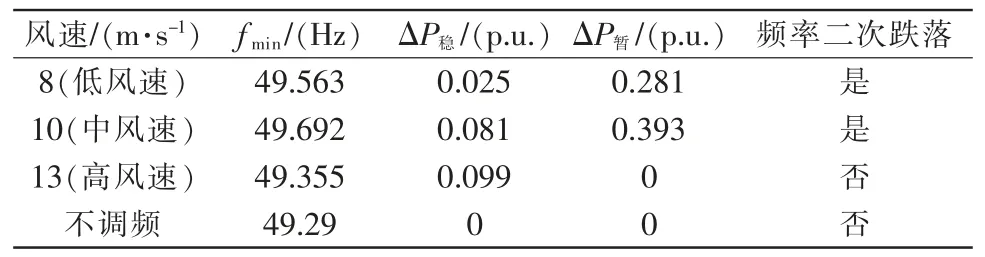
表6 仿真关键数据Tab.6 Simulation key data

由表6 可知，DFIG 参与系统调频时，系统的暂态频率跌落，在中风速时改善最为明显，低风速次之，而高风速时对暂态频率的跌落没有任何改善，系统达到稳态时，DFIG 有功功率支撑则为低、中、高风速依次增加，符合预期调频效果。

4 结语

双馈风力发电机采用变系数控制时能够根据风速的不同充分利用风能响应系统的频率变化，风速越大，下垂系数越大，减载运行的双馈风力发电机调频结束时增发的有功功率越多，减小同步发电机组的调频压力。减载控制为双馈风力发电机提供了备用容量，能够有效抑制频率的二次跌落。惯性控制能够快速降低转子转速，释放转子动能来响应系统频率变化，改善调频效果。