喷气协助航行体入水空泡流动特性实验研究
邹志辉,李 佳,杨 茂,刘红松,蒋运华,4
(1.中山大学 海洋工程与技术学院,广东 广州 510275;2.哈尔滨工程大学 航天与建筑工程学院,黑龙江 哈尔滨150001;3.重庆长安工业(集团)有限公司,重庆401120;4.南方海洋科学与工程广东省实验室(珠海),广东 珠海519000)
入水问题广泛存在于航空航天等工程领域,如水上飞机着陆、航天器部件水上回收、空投鱼雷、水中兵器跨介质等,其研究主要集中在入水冲击、空化及水中弹道等方面。入水初期物体会与水面产生强烈的非线性冲击,对物体产生巨大的影响,且存在入水物体结构损坏、装置失灵及弹道失稳等问题。对入水问题较为系统的研究可以追溯到1929年KARMAN对水上飞机降落冲击载荷的研究,结合动量守恒理论提出了附加质量的概念,给出了计算入水冲击载荷的一个近似公式。随后众多学者基于KARMAN的动量冲击理论从理论、实验和数值模拟等方面对入水冲击问题进行了大量研究,这些工作主要聚焦于对入水冲击载荷的预测。自CHUANG首次发现物体在入水过程中底部与液面之间始终存在一层气垫以来,后续相关学者对其进行了验证并讨论了气垫的存在对入水产生的一些影响。HUERA-HUARTE等、OKADA等及ERMANYUK等的研究结果表明,由于存在缓冲效应和由此产生的夹带空气滞留,空气垫可以显著影响冲击压力、冲击模式、冲击时间和喷流形状等。曹正林等的研究结果也表明空气垫的存在大大减少了砰击压力峰值。这些研究表明入水过程夹带的空气可以作为减缓入水冲击的介质,但几乎没有学者通过人工通气(喷气)的实验去验证入水减缓效果。近年来射流缓冲的概念逐渐被提出,JIANG等使用气射流作为空化器产生超空泡来降低航行体的阻力,并进行了不同通气量的入水实验研究,表明喷气协助入水有望成为减缓航行体高速入水冲击的方法。同样,SPEIRS等开展了物体与水射流同时冲击水面时空化与载荷特性的实验研究。本文主要进行了向前气射流协助航行体入水过程空泡多相流动特性的实验研究,此研究可为后续实施喷气协助入水提供一定的认识。
1 实验设置
1.1 实验装置
实验系统主要包括水箱、高速成像系统、供气系统、航行体入水系统及入水航行体,如图1所示。供气系统由高压气瓶、调压阀、气体流量计及若干气管组成。喷气流量是在标准条件(273 K、100 000 Pa)下用标准升每分钟来确定。气体流量计选用欧米伽FL2044,全刻度读数为100 L/min,以满足本文研究中使用的0 L/min到45 L/min不同气体流量。此外,气体流量计不确定度是满量程读数的3%。航行体入水系统由导轨、导轨支架及滑块组成。导轨置于上下导轨支架上,方便调整航行体入水角度。导轨总长4 m,宽0.038 m,底部固定一缓冲块用于阻停滑块,保护水箱及入水航行体。入水过程是将航行体固定于滑块上,滑块置于导轨由静止释放,在重力作用下自由下滑。滑块释放最高点和水箱底部分别距水面2.223 m和0.79 m。入水速度受多重因素干扰,且由于多次重复性实验,滑块与缓冲块的冲击导致航行体与滑块固联出现松动,引起入水姿态有所偏差。因此,入水速度和入水角度根据实验图像来测量,其不确定度分别为2.24%(36°)、3.56%(45°)及5.62%(50°)。
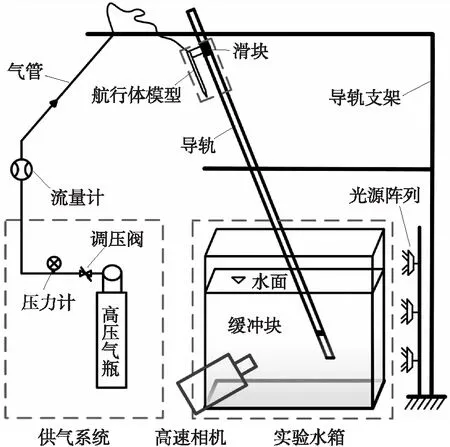
图1 实验系统示意图
入水航行体是由主体段和头部段组成的圆柱组合体,材质为表面经过抛光处理的铝。头部段形状为平头并设置=3 mm的喷口,平头空化器直径=10 mm。主体段最大直径=26 mm,模型总长=260 mm。模型内设置通孔连接气体管路,具体见图2。
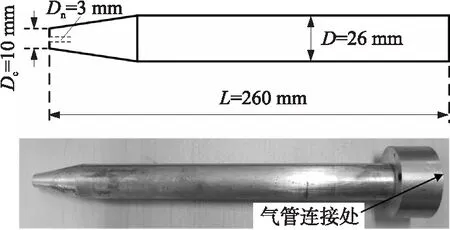
图2 实验航行体模型
1.2 实验方法与理论
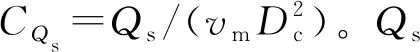

图3 航行体运动不同阶段示意图
所有结果以无量纲的形式表现,定义无量纲参数均基于喷口直径,分别为(开口空泡深度),(开口空泡直径),(空泡直径),(射流长度),(航行体模型距液面垂直高度),(航行体模型穿过液面后距液面的垂直高度)。另外需要说明的是,实验中在小喷气系数的情况下(<045)观察不到空泡的形成,因此结果分析主要是在>045范围进行。
1962年BANKS等在气射流垂直冲击液面变形问题中提出驻点压力法分析射流冲击自由液面形成的空腔形态。驻点压力法将射流在空泡驻点产生的动压与空泡深度关联,即:

(1)
式中:,分别为气射流和水的密度;为驻点处气射流速度;为表面张力;为驻点处曲率半径。
分析图3(a)所示的喷气入水过程,其驻点处气射流速度可以根据湍动射流轴线速度分布估计,即:
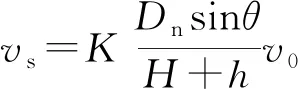
(2)
式中:为湍动射流轴线速度分布经验常数,为入水角度,为射流核心区轴线速度。
喷气入水运动过程中射流在驻点处产生的动压为

(3)
式中:为模型运动速度。
考虑到入水过程时间极短,取入水过程的平均速度,因此本实验假设在入水过程中航行体动量不变。在计算过程中忽略表面张力的影响,结合式(1)~式(3)有:

(4)

2 实验结果
2.1 实验现象描述
根据实验现象,可以将喷气入水过程分为液面振荡、喷溅、形成流动和空泡形成4个阶段。图4是=09,=45°,=18条件下喷气入水空泡流动演化过程。起初在航行体距液面一定距离时,受射流本身特性影响,液面未受到射流扰动,表现出静止状态(图4(a))。当航行体运动至射流影响范围内,由于扩散的湍动气射流随航行体加速前进,斜冲击到液面在气液界面形成剪切层,并通过黏性作用加速液体使液体和气体发生动量交换并强烈混合,形成了表面振荡现象(图4(b))。这种表面振荡不稳定现象与HWANG等在实验中提出的K-H不稳定一致。随着航行体距液面高度的减小,振荡扰动逐渐增强(图4(c)),之后开始出现液滴飞溅(图4(d))。由于入水的非对称性,飞溅出现在左侧并受重力影响回流持续影响液面。当航行体持续接近液面,气射流动量增加使得液面在航行体未达到液面表面就形成凹陷(图4(d)),并进一步发展成开口空泡(图4(e)),同时气射流夹带的空气也进入空泡。此时,射流前方的液体持续被排开,开口空泡深度和直径由于射流和航行体传递的动量逐渐扩张(图4(d)~图4(g))。值得注意的是,在空泡发展过程中气射流在空泡内出现了大量的回流,空泡壁面出现明显的波动(图4(e)~图4(j)),这种波动除了和气液剪切有关,还可能和湍动射流压力脉动有关。在整个向前喷气协助入水过程中空泡壁面粗糙,空泡整体形态受重力影响呈上浮趋势。

图4 向前喷气入水过程空泡形成及演化过程
此外,在较大喷气系数下,射流产生的通气空泡在整个入水过程中能时刻包裹运动的航行体。但是在小喷气系数下,由于射流动量过小,环境压力增大(入水深度增加所致),能够维持有效空泡形态的驻点压力小于随航行体运动变化的环境压力,最终未达到闭合或已经闭合但未溃灭的通气空泡遭到航行体的冲击而产生湮灭现象。图5给出了=07,=45°,=18条件下的通气空泡“湮灭”过程。空泡“湮灭”发生后,航行体湿面积增加,入水阻力增大。但由于持续性的射流及其脉动,航行体在运动过程头部存在云状气泡或泡状流逐渐上浮。

图5 空泡“湮灭”的过程
2.2 开口空泡流动特性
2.2.1 模型高度对开口空泡的影响
一般来说,射流完全发展时其轴线速度分布较为稳定,但由于航行体处于运动状态,动态的射流与液面间的距离时刻变化会导致作用在液面的射流速度时刻在变化,进而对液面产生不同的影响。图6给出了=14,=36°,=18条件下航行体在不同高度形成的开口空泡形态演变过程。在开口空泡形成的过程中,发现存在明显的区域转变。这些区域包括液面振荡区、过渡区和空泡形成区。从液面振荡区转变为空泡形成区时,过渡区是逐渐向右侧转移并逐渐转变为空泡形成区,如图6插图。这种区域的转变归因于动态的射流,具体来说,在湍动射流发展中,扩散的射流夹带周围的空气使其宽度不断增长形成混合区,射流与液面作用先接触射流混合区,其次是射流核心区。同时由于射流在发展过程中其重力与浮力不平衡导致射流整体向上弯曲。因此,在这个过程中射流宽度相当于一个收缩的过程,导致自由液面受影响范围逐渐减少,并逐步转变而影响区域形态。在入水过程中,气射流在自由液面形成水平方向的剪切速度和竖直方向的冲击速度。水平方向的剪切作用是液面振荡区形成的主要原因。但由于液体静压和表面张力的作用,在液面振荡区自由液面始终存在振荡行为而不形成明显的穿透现象,如图6液面振荡区所示。随着航行体高度的减小,射流轴线冲击速度逐渐增大,液面振荡过程逐渐向形成开口空泡过程转变,如图6过渡区所示。液面振荡区逐步向空泡形成区转变后,射流穿透液面明显,形成的开口空泡深度加深,且液面振荡现象逐渐消失,空泡形成区出现,如图6空泡形成区所示。当航行体进一步下降,开口空泡直径和深度逐渐增大,入水通气空泡形成。从图6中可以看出,通气空泡形成后,穿透深度随航行体的运动逐渐加深,并形成非对称空泡轮廓。

图6 航行体在不同高度下形成的开口空泡形态演变过程
图7给出了=14,=45°,=18条件下的无量纲开口空泡深度随无量纲航行体垂直高度的变化。从图7中可以看出,在喷气系数一定的情况下,入水过程中开口空泡深度随着航行体垂直高度的减小逐渐增加,当航行体头部到达液面时,穿透深度达到最大。航行体的运动缩短了射流离液面的距离,使得作用在液面的射流速度(射流动量)变大,导致形成的空泡变深。图7中虚线是同一条件下的理论结果,可以看出和实验符合良好,且表明这种增长并非呈线性增加。
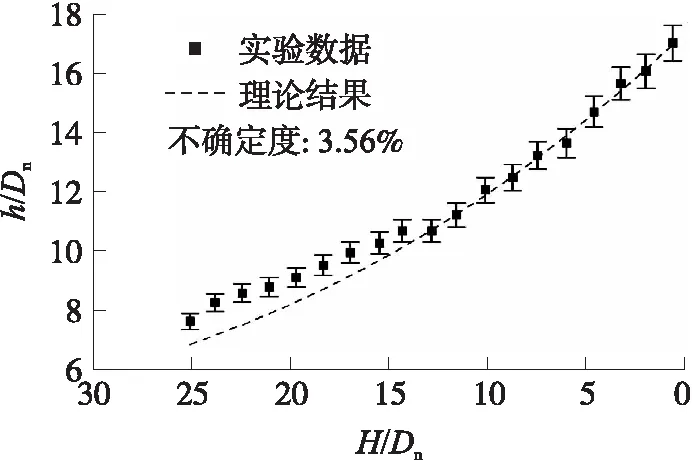
图7 空泡深度随航行体高度的变化
图8是同一条件下无量纲开口空泡直径与航行体高度的关系。很明显,开口空泡直径在入水初期随航行体垂直高度的减小逐渐增加,但到达一定值时空泡直径不再增加,而出现减小的趋势。初期开口空泡直径的增加同样是由于垂直高度的变化引起射流动量的增加,导致空泡两侧被排开的液体逐渐增多,使得空泡直径变大。而当射流穿透液面并发展空泡向前运动时,受空泡内压和静压的影响,液面表面开始出现闭合行为,空泡直径呈减小的趋势。
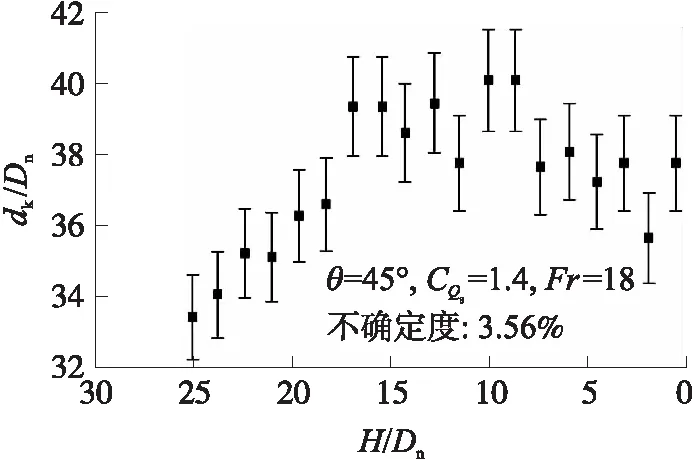
图8 空泡直径随航行体高度的变化
2.2.2 喷气系数对开口空泡的影响
图9给出了航行体位于一定高度下(=14)开口空泡深度和直径与喷气系数的关系。航行体在一定高度下,根据湍动射流轴线速度分布规律,喷气系数越大的射流动量越大,形成的开口空泡深度和直径越大,呈明显的线性变化规律。
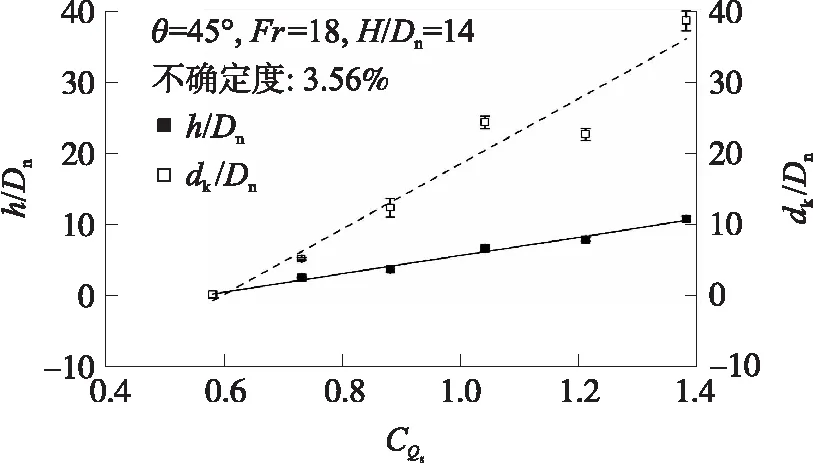
图9 空泡深度和直径随喷气系数的变化
值得注意的是,空泡直径和深度表现出的线性关系斜率相差较大,约为3.5倍。也就是说喷气系数对开口空泡直径的影响相对于空泡深度更为敏感。这种敏感的原因在于空泡形成初期射流首先与液面作用,水平方向的气射流沿液面运动形成气液界面不稳定,而垂直方向则穿透液面形成空泡。当喷气系数增大时,自由液面失稳振荡越强烈,形成的开口空泡波动范围越广,这种波动沿着射流运动方向传递,直到射流动量完全被消耗为止,此时在自由液面形成的波动范围(初期空泡)要远大于气射流在竖直方向穿透液面的深度。
2.2.3 入水角度对开口空泡的影响
图10给出了航行体处于一定高度时开口空泡深度和直径与入水角度的关系。可以观察到,前期随着角度的增加,开口空泡深度呈现增加的趋势。主要原因可以考虑两点:①入水角度越小,射流流动主要沿液面水平方向呈气液剪切流动现象,对垂直方向影响较小,导致穿透深度越小;②入水角度越小,航行体处于同一高度时射流发展到自由液面的距离越远,射流动量越小,形成的空泡深度越小。而对于空泡直径与入水角度的变化关系也可以用前面深度变化和2.2.1节解释。

图10 空泡深度和直径与入水角度的关系
此外,在实验进行的工况中,当入水角度增加到一定值时,会出现角度增加而穿透深度减小的情况,如图10所示。这可能存在某个临界入水角度使得垂直和水平分量的射流动量产生最大的穿透深度。
2.3 空泡发展流动特性
2.3.1 空泡壁面波动
实验发现,在航行体穿越气液界面之后的空泡流动中,当06≤<09时会出现明显的空泡壁面波动现象,这种波动的发生会显著影响空泡的稳定性。图11给出了典型情况下(=06,=36°,=18)的空泡壁面波动的形成过程。入水后在一定时间内形成的空泡壁面并未发生明显的波动,如图11(a)。而此后由于射流不断喷出,气体在头部沿空泡壁面回流出现较小的空气核,空气核迅速成长为孤立的附壁气泡,如图11(b)。由于空泡内存在回流的气体,气泡随气体回流运动形成游移的附壁气泡群,如图11(c)。随着航行体与回流的气体进一步运动,游移的气泡群由于空泡内部压力变化和气液剪切作用发生溃灭,如图11(e),并在空泡壁面不断形成波动。随着航行体的运动,波动逐渐沿气体回流方向传递,直到波动停止,如图11(h)。

图11 小喷气系数下空泡壁面波动形成过程
由于在运动过程中一直存在射流喷出,这种波动会一直跟随入水空泡的发展,严重影响空泡的稳定发展。这种波动现象与JIANG等的研究类似,通过对射流长度进行频谱分析,发现频谱表现的一般特征与HWANG等的射流撞击实验中气液界面的振荡相似。HWANG等对空泡深度和气体射流内部的压力波动进行了谱密度分析,表明空泡深度与气体射流中的湍流波动之间存在联系,同时根据JIANG等的频谱分析,认为射流长度的波动也可能与驻点附近的气射流湍流波动有关,而射流长度的波动会显著影响气核和壁面波动特性。
2.3.2 空泡直径
航行体穿越气液界面后,空泡直径决定气射流形成的空泡能否有效包裹航行体而产生缓冲减阻效果,因此以为参考监测入水过程空泡直径的变化显得很有必要。图12给出了空泡直径随时间的变化情况。图中可以看出空泡直径随时间变化呈先增加后减小的趋势。根据的定义,在初始时刻航行体到达自由液面时开口空泡已经形成,航行体进一步运动后射流动量增加,气体增多,使开口空泡进一步扩张,因此开始空泡直径呈现增长趋势。待航行体头部穿越自由液面后,射流继续加速液体前进,形成较为稳定的空泡形态。但随着运动的进一步发展,空泡直径的扩张速度小于航行体的运动速度,空泡直径开始出现下降趋势,如图12插图所示。通过插图也可以明显地看出空泡直径的变化状态,但在入水后期即便是环境压力逐步增大,空泡直径减小的趋势也不太明显,基本稳定在约3倍空化器直径,这和射流压力、空泡内压有显著的关系。

图12 空泡直径随时间的变化(插图为对应的空泡状态)
图13给出了不同入水角度下,航行体处于一定运动时刻(=15 ms)空泡直径随喷气系数的变化。很明显,在某一入水角度下空泡直径随喷气系数呈线性增加,但不同入水角度间其线性关系几乎一致,这也说明入水角度对空泡直径影响有限。

图13 空泡直径随喷气系数的变化
2.3.3 射流长度
对气射流协助入水而言,航行体穿透自由液面之后空泡和射流稳定发展是协助入水的关键,而射流长度影响航行体能否稳定排开入水前方液体形成有效的降载减阻空泡。图14给出了射流长度随时间变化趋势。可见射流长度随着航行体的运动逐渐减小,这可以通过运动过程中压力平衡的观点来解释,在入水过程中,航行体速度由于射流的反向作用力逐渐减小,同时随着穿透深度的加深,环境压力逐渐变大。根据BANKS等提出的驻点压力分析法,可知在入水运动过程中空泡最深处的静压=。静压随着模型的运动逐渐增大,在喷气系数不变的情况下要维持射流驻点处的动压来平衡逐渐增大的静压,则射流驻点处的速度就需要增大,根据湍动自由射流轴线速度分布规律,这样就要求射流长度减少。
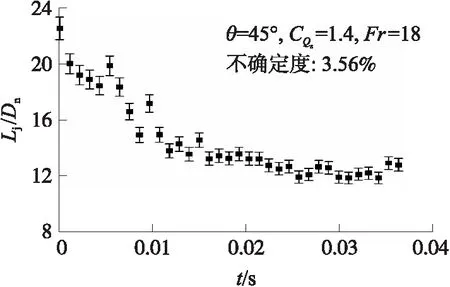
图14 射流长度随时间的变化
到运动后期运动射流长度和空泡直径一样,均衰减不显著。随着航行体穿透深度的增加,射流长度发生变化会引起驻点处速度的变化。为了解射流在穿透过程中驻点处速度的脉动变化,图15分别给出了=14,=45°,=18条件下航行体运动至=15 ms时刻之后驻点处射流速度和空泡直径径向扩张速度随时间的变化情况。驻点处射流速度由式(2)计算,空泡直径径向扩张速度根据实验图像提取的空泡直径对时间的变化率确定。在穿透深度较小时,随着穿透深度的增加,驻点处射流轴线速度逐渐增大,且表现出脉动变化。在图16中,速度功率谱密度整体显示出减少的趋势,但在()=168 Hz时出现一个极小值。空泡直径径向扩张速度同样显示在穿透后期处于周期性脉动变化,如图15所示。通过频谱图可以看出,空泡直径扩张速度功率谱密度和射流驻点处速度功率谱密度高度相似,且均出现了一个极小值,而且出现极小值时两者的频率很相近(()=168 Hz,()=124 Hz)。因此,可以认为在入水穿透后期,空泡直径和射流长度不仅受环境压力的影响,还和湍动射流脉动有关。

图15 射流驻点处速度和空泡直径径向扩张速度与时间的关系
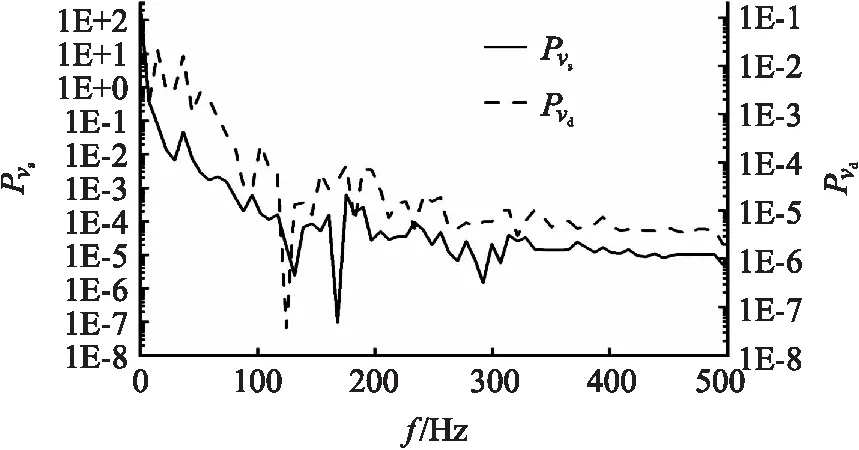
图16 射流驻点处速度和空泡直径径向扩张速度相对应的功率谱密度
图17给出了喷气系数对射流长度的影响,同样考虑的是航行体在=15 ms时刻的情况。图中可明显看出射流长度随喷气系数的增加仍然呈线性增加,并且在不同角度下其关系也基本一致。因此,入水角度对射流长度的影响也不太显著。

图17 射流长度随喷气系数的变化
3 结论
本文研究了向前喷气协助航行体入水通气空泡多相流动特性,进行了不同喷气量、不同入水角度的向前喷气入水实验。分析了入水过程中射流穿透水面初生空泡的形态及空泡的发展,探讨了不同喷气量、入水角度对空泡形态、射流长度等的影响。主要结论如下:
①喷气入水与直接入水相比,入水初期存在液面振荡和空泡“湮灭”等现象;入水后由于K-H不稳定空泡壁面出现波动。
②喷气入水形成空泡流动过程存在3个区域转变,分别是液面振荡区、过渡区和空泡生成区。这些区域的形成与航行体位置有关。
③入水初期,开口空泡深度随航行体高度的减小而增加;直径随航行体高度的减小先增大后减小;喷气系数与开口空泡深度、直径呈线性关系,且对开口空泡直径的影响相比于开口空泡深度更为敏感。
④航行体穿越液面入水后,空泡直径和射流长度在入水运动过程中均逐渐减小,但后期衰减不明显,这些变化不仅受环境压力的影响,还和湍动射流脉动有关。空泡直径和射流长度随喷气系数呈线性增加,入水角度对空泡直径和射流长度的影响有限。

