基于Matlab 的马科维茨投资组合理论的实证研究

夏 雪

一、前言

马科维茨投资组合模型，是投资学中一种重要的科学理论模型。它通过对所有资产的历史数据进行分析，在保证风险水平不变的同时获取最高的收益，为投资人提出了具有科学依据的量化资产配置的方案。本文以马科维茨模型为理论基石，借助Matlab 的Portfolio 金融工具箱，选取汇添富上证综合指数基金中具有市场代表性价值的4 支股票展开案例分析，采用2017 年1 月1 日—2021 年8 月1 日的日频收盘价数据，构建均值—方差模型和投资组合有效边界模型，计算出夏普比率最大的股票投资组合，实证检验马科维茨模型在股票投资中的作用。

二、相关理论分析

（一）马科维茨模型的基本原理

1952 年，Markowith 首次提出利用均值—方差模型量化计算投资者的资产组合问题。该模型利用概率论的基本思想，假定所有资产的收益呈正态分布，用资产收益的历史均值衡量投资回报率，用资产收益的历史方差衡量投资风险[1]。这样资产选择问题就被转化为能定量测算的二次投资规划问题。这就是马科维茨投资组合理论的基本原理。

股票收益的协方差代表股票收益情况的相关程度。协方差为0 时，说明几支股票的收益不相关。协方差为正时，说明几支股票收益呈现正相关关系，协方差越大，正相关性越强，一赔俱赔，不利于分散投资风险；协方差为负时，说明几支股票收益呈负相关关系，有利于分散投资风险。

我们希望在投资组合中看到有赔有赢的情况，尽量避免一赔俱赔。因此选择股票时应尽量选择相关度低的股票[4]。

（二）马科维茨模型的假设条件

（1）证券市场是有效的，即证券价格能即时准确地反应市场信息，所有交易者获得的投资信息没有差异性；

（2）市场上没有交易成本和税收，每个投资者都可以自由进出市场不受限制；

（3）投资者是理性的。所有投资人都是风险回避者；

（4）投资人只根据投资组合的收益率和风险做判断，投资者了解不同资产的收益情况；

（5）所有资产的收益率都是不确定的，不同资产的收益之间具有相关性。

（三）马科维茨模型的建立

基于上述假设条件，马科维茨建立了计算有效投资组合的均值—方差模型。

模型如下：

限制条件：

其中，rp为股票组合的收益，ri、rj分别是第i、j 支股票的收益率，xi、xj为股票i、j 的投资权重，σ2（rp）为组合的投资方差（表示该投资组合的投资风险），Cov（ri，rj）是两支股票之间的协方差。

上式的理论意义是，当设定好投资组合的预期收益率后，可以使用上式算出风险最小化的投资组合。不同的期望收益率对应不同的投资组合和不同的最小方差，这就形成了预期收益率最大和风险最小的投资组合。

（四）夏普比率

夏普比率是Sharp 在马科维茨模型的理论基础上发展出来的，是衡量投资组合有效性的重要指标。它衡量的是投资者每多承担一单位的风险，可以获得的超额投资收益率[2]。夏普比率的计算公式如下：

E（Rp）代表投资组合的预期收益率，Rf代表无风险资产的投资收益率，两者之差代表的是风险投资的超额收益率。σ 是投资组合的标准差，代表投资组合的风险。

夏普比率值越大，表明投资组合单位风险上的超额收益越高，更具有投资价值[3]。本文实证部分将使用夏普比率衡量资产投资组合的有效性，用Matlab 找出有效前沿曲线上的最大夏普比率点，作出资产配置线。

三、实证分析

（一）实证假设

根据中国股票市场的实际情况以及理论分析的方便，本文实证研究作出以下假设：

（1）马科维茨模型的预设条件：

资本市场完全有效，投资者的交易成本为0，并可以自由选择交易的资金份额；投资者完全依据投资组合的期望收益和标准差作投资决策；投资者是报酬不厌足的，同样的风险下，会选择期望收益率更高的投资组合；投资者属于风险规避类型。

（2）卖空约束：依据中国股票市场的交易机制，假设不允许卖空。

（3）不考虑转股对报酬率的影响。

（二）样本选取

本文选取的是汇添富上证综合指数基金中具有代表性的4 支股票。贵州茅台（600519），农业银行（601288），中国石油（601857），海天味业（603288）。

本文中用到的资产价格数据来源于国泰君安数据库，选取2017 年1 月1 日至2021 年8 月1 日总计1114 个交易日的股票日收盘价。期间中国证券市场既有持续上升，也有持续低迷。因此选择在这一样本区间内开展实证研究，有很大的典型意义[5]。

（三）基于Matlab 的实证分析

本文将收集的4 支股票的日收盘价作为资产价格，首先利用price2ret 函数将资产价格转化为资产的投资收益率，得到4 支股票的资产列表。

1.股票期望收益率与协方差矩阵的获取。利用Matlab的金融工具箱创建portfolio 对象，利用portfolio 中的工具，得到4 支股票的期望收益率和协方差矩阵。

4 支股票的相关系数矩阵如表1 所示。从表1 中可以看出，每两支股票间的相关系数均小于1，且比较接近0。可以说明4 支股票的相关性很弱，出现一赔惧赔的几率较小。因此同时投资这四种股票，可以帮助投资者有效分散风险。

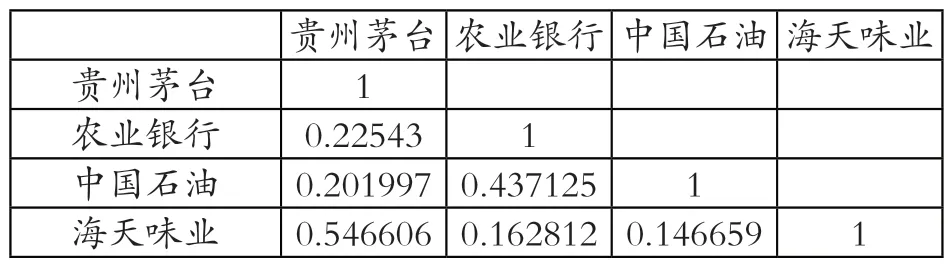
表1 相关系数矩阵

2.有效前沿曲线的构建。将4 支股票的期望收益率和方差设定到投资组合优化问题中，并限制所有资产的比例和为1，对4 支股票进行投资组合优化[6]。

横轴代表股票的风险（收益率的标准差），纵轴代表股票的收益（收益率），可视化各项资产的期望收益率和风险，即可作出有效前沿曲线，如下图3 所示，蓝色曲线是风险资产的有效前沿曲线，曲线上每个点都代表一个有效的投资组合。

3.包含无风险资产的有效边界曲线的构建。在现实的投资问题中，为保证一定的收益，投资者往往也会投资无风险资产。本文将无风险资产的收益率设置为0.015，通过连接无风险利率资产点和有效边界曲线上的点，可得到不同的资产配曲线，最优的资产配线是无风险资产点在有效边界曲线上的切线，切点为最大夏普比率点。

如图1 所示，Cash 表示无风险资产点；Sharp Ratio表示最大夏普比率点；CAL 是最优的资本配置线，表示投资组合和收益率风险的线性关系，它和有效边界曲线的切点即为最大夏普比率点。

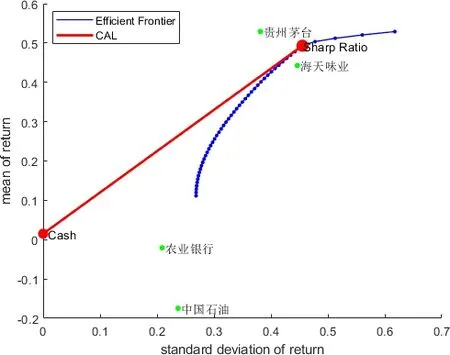
图1 无风险资产和风险资产组合的资本配置线

4.根据目标收益率和风险构建。投资组合作出无风险资产和有风险资产的投资组合的有效边界曲线，如图2所示。并计算出有效边界曲线的收益率区间和风险区间。

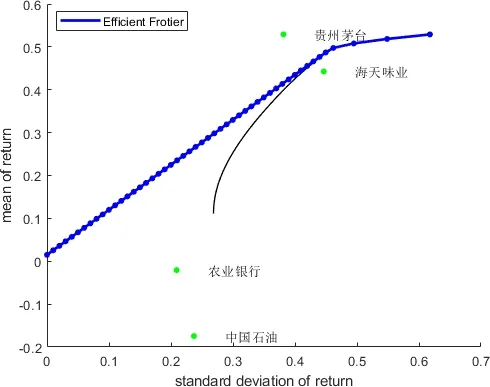
图2 无风险资产和风险资产投资组合的有效边界曲线

最终得到投资组合的收益率区间为[0.1113，0.5290]，风险区间为[0.2685，0.6176]。设定目标收益率 TargetRet=0.25 时，需要承担的风险值为0.2985，得到4 支股票的分配比例为贵州茅台（0.3233），农业银行（0.2678），中国石油（0.1564），海天味业（0.2526）。

设定目标收益率 TargetRet=0.40 时，需要承担的风险值为0.3818，得到4 支股票的分配比例为贵州茅台（0.4692），农业银行（0.1796），中国石油（0.0000），海天味业（0.3512）。

四、实证结论

（一）结果分析

MATLAB 的金融工具箱（Financial Toolbox）提供的Portfolio 工具支持马科维茨投资组合理论的均值-方差分析方法和投资组合有效边界模型，根据各个证券的历史收益数据，Matlab 使用很少的代码量就可以计算出有效的投资组合集合，大大简化了我们的计算流程。

在上述实证研究中，如果投资者对上述4 支股票进行最优化组合，要想将预期收益率从0.25 提高到0.40，投资者需要承担的风险会从0.2985 提高到0.3818，此时的最优投资组合仅对其中3 支股票做了最优化组合，中国石油被分配的投资比例为0。因为该股票的投资收益率是4 支股票中最低的，且远远低于农业银行的投资收益率，但投资风险又高于农业银行。

这种结论也证实了马科维茨的资产组合理念：把资金分配到不同类别的资产上，就能够在实现预期收益率的同时有效分散资产风险，从而帮助投资人实现财富效用最大化。而较小的股票组合在提升投资人预期收益率的同时，也提高了投资风险。而且，马科维茨组合采取的优化方式，排除了那些低收益、高风险的股票，有效组合的证券数目较少，有利于帮投资人把主要精力放在投资比例较大的股票上，减少投资的盲目性。

（二）马科维茨模型存在的问题

首先是市场有效性问题。马科维茨模型的假设之一是市场是有效的，即证券价格能够充分即时准确地反映市场上各家公司的信息。投资者不需要成本就可以无差异地获取这些市场信息，并根据市场信息做出投资决策。随着大数据时代企业信息披露的增加，我国证券市场的有效性在逐步增强，但仍未达到弱有效[7]。

其次是风险测度问题，马科维茨模型的前提是证券的历史收益率服从正态分布，但是越来越多的实证研究都对这一假设提出了质疑。

最后是交易费用问题，马科维茨模型没有考虑证券组合投资过程中的交易费用。但在实际情况中存在交易费用，并且会影响投资者随时调整投资组合。忽视交易费用的投资组合可能产生非有效的证券组合投资[8]。

引用

[1]Markowitz H.M.Portfolio Selection [J].Journal of Finance.1952(7).

[2]Sharpe,William F.A Simplified Model for Portfolio Analysis [J].Management Science,1963,9(2):277-293.

[3]Sharpe W.Capital Asset Price: A theory of Market Equilibrium under Conditions of Risk [J].Journal of Finance,1964,19(3):425-442.

[4]张贺清.均值和方差变动的马科维茨投资组合模型研究[D].哈尔滨工业大学,2015.

[5]曾颖苗,张珺,张晴.马科维茨模型在股市最优投资组合选择中的实证研究[J].湘潭师范学院学报(社会科学版),2009,3104:88-91.

[6]杨晓春.马科维茨有效边界理论的实证分析[J].陕西理工学院学报(自然科学版),2008,04:85-89.

[7]吴昆晟.马科维茨模型在 A 股市场中的应用分析[J].新经济,2015,26:50.

[8]王小敏.马科维茨理论的实际运用[J].时代金融,2013,18:251.