相位解缠算法对比研究

施慧宇，王延霞，杨海燕，程子莹，夏奇亮，欧阳龙

(滁州学院 地理信息与旅游学院，安徽 滁州 239000)

相位解缠是InSAR数据处理中至关重要的一步。解缠方法正确与否直接关系最终结果的可靠性。近年来，InSAR相位解缠算法不断得到优化。目前,相位解缠算法主要包括路径追踪算法、最小范数算法和网络流算法[1-3]，文中主要通过选取并对比3种代表性的解缠方法，寻找最适合低相干区的解缠方法，为后续时序InSAR在地面沉降监测方面的应用提供参考[4-7]。

1 相位解缠基本算法

1.1 路径追踪法

路径跟踪法是指按照某一原则确定积分路线，限制潜在误差。比如在两个InSAR图像受到干扰后，可以获得一个绕组相位图像，每个像素的值是相应干涉相位的主要值。根据奈奎斯特定理，当相邻像素之间的相位差小于2时，相位的实际值可以通过积分算法恢复。假设已知在某一点像元x0处的相位，则任意其他像元x处的相位可由式(1)求得。

(1)

式中:φ(x)为像元x上的解缠相位;Δφ为φ的相位梯度;C为解缠区域中连接起始点r0和r的积分路径;φ(x0)为像元x0上的已知解缠相位，由积分

(2)

求得。由式(2)可得，I的线性积分取决于积分路径C的起始点和终止点。若使C与积分无关，则需

∮F(x)dx=0

(3)

积分成立。

二维相位解缠通常选用式(3)作为依据来判断积分是否跟路径有关[8]。在InSAR数据中，部分数据的积分路径不满足式(3)的基本条件。也有部分数据因为地形起伏本身就不能满足相邻相位缠绕之间差值的绝对值不小于π等其它的原因[3,9]，会造成闭合路径积分无法沿某条积分路径完成积分。在InSAR中，这些像元的相位被称为电荷，电荷包含正负两种。在路径积分法中，如何实现正负电荷偏移(称为“分支”)来阻止积分路径通过这些分支是重点研究的问题[10]。文中以路径追踪法中较为典型的区域增长法作为实验方法进行对比实验。

1.2 最小二乘算法

最小二乘法(Minimum Cost Flow)可以通过全局来拟合已经观测的相位缠绕，从而得到最接近的原始的相位缠绕。当P=2时最小范数法就是所提到的最小二乘法。最小二乘法的求解过程为

φi+1,j-2φi,j+φi-1,j+φi,j+1-2φi，j+φi,j-1=ρi,j，

(4)

(5)

其中,像这种无加权算法的解缠原理就是通过寻求解缠相位值的离散偏微分与缠绕相位值的离散偏微分之间差值，取差值的绝对值最小，得到解缠相位的真值，从而使式(6)结果最小。

(6)

最小二乘法最致命的缺陷之一就是只能得到整幅影像良好的解缠结果。图像质量较好的区域会因为最小二乘法原理被图像质量很差的某一区域严重地影响解缠精度，也有可能因噪声或“去相干”影响解缠精度[11]。从最小二乘法被提出以来，这个问题就一直没有得到解决。

最小二乘法其算法并不是加权的，而是通过残差点区域进行计算，因此，得到的结果可能不太理想，太过平滑，所以需要加入权重。最小二乘法在展开的时候，残差点太多、噪声过于严重的数据会导致相位解缠的结果太过平滑，这个时候可以引入加入权重的最小二乘法进行补偿，使结果与真实相位的值更加接近[12]。如果将原始的相位解缠数中的每个点都加上对应的权重数据，就可以将其转变为加权最小二乘法问题[13]。

1.3 Delaunay MCF网络流算法

网络流算法主要分为基于不规则网络的最小费用流算法(Delaunay MCF)和基于网络的最小费用流解缠算法两种。Delaunay MCF的主题思路是：先查找相干系数较高的相位，将其提取成高质量相位集合，然后使用Delaunay三角网识别这个三角网中的残差[14]，使这些高质量的相位数据的正负残差点进行连接，建立枝切线。最后可以使用穿过枝切线的方法求解积分[15]，得到最终的相位解缠结果。

2 实验与分析

2.1 技术流程

文中实验所用工具为ENVI SARscape。首先，将ENVI SARscape系统中的最小二乘法、区域增长法(Region Growing)、Delaunay MCF 3种方法进行理论方面的对比研究和差异性探讨。然后结合自选数据在ENVI SARscape中分别使用3种方法进行相位解缠，根据相位解缠的结果进行分析，得到Delaunay MCF与其它两种方法的差异性和优缺点。将生成的解缠结果图进行视觉上的对比，得到初步结论，随后使用软件ENVI SARscape进行阈值参数的变换，得到最优阈值参数，最后对解缠结果进行精度评定、解缠效率对比分析，重复以上步骤得到最终结论。

2.2 不同方法下的相位解缠

文中第一个实验采用在固定阈值参数(系统默认的参数)的情况下，用最小二乘法、区域增长法及Delaunay MCF 3种方法进行试验，比较出使用3种方法的相对优缺点，此实验反复多次进行并得到结论，选择其中一组数据进行结果分析。

通过表1、表2、表3可以了解到在同一位置时3种方法的统计差值(Cursor Value)，在任一位置时最小二乘法的统计差值总是小于区域增长法和Delaunay MCF，但3种方法的任意某两点之间的差值却基本相同。因此，最小二乘法相对于区域增长法和Delaunay MCF相位解缠的结果图像更为平滑；区域增长法比Delaunay MCF的解缠图像更为平滑。

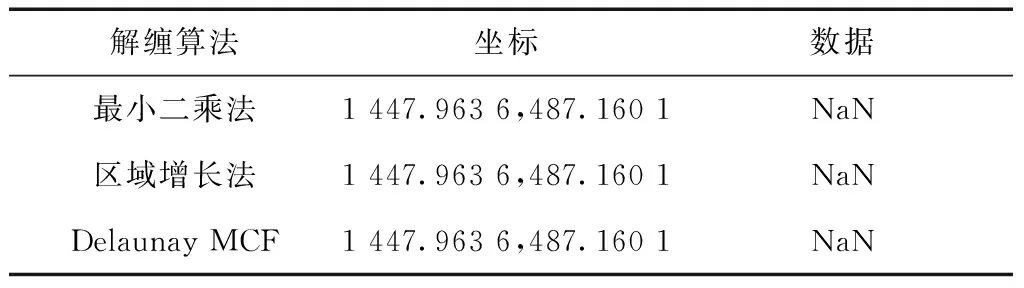
表1 3种算法在同一光亮位置时的统计差值

表2 3种算法在同一黑暗位置时的统计差值

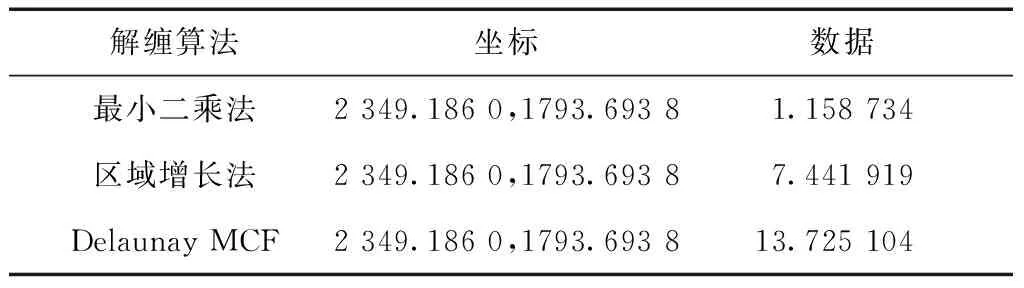
表3 3种算法在同一灰色位置时的统计差值

2.2.1 区域增长法

由图1可知，区域增长法的优点是同时考虑到多个方向的相位解缠信息进行解缠，具有很好的解缠精度和准确性。但是在噪声过大的区域，相位变化的部分在解缠后的图像上会出现“解缠孤岛”[3]。因此，该方法减少了由相位突变引起的误差，使得相位信息无法恢复，整个图像甚至可能会无法使用。

图1 3种相位解缠结果

2.2.2 最小二乘法

从图1可知，最小二乘法最终解缠结果受到低相干区域误差的影响，使低相干区域的误差累计到全程。总体来说最小二乘法的解缠效率偏低，但其解缠精度较高，解缠结果更为平滑。

2.2.3 Delaunay MCF网络流算法

区域增长法、最小二乘法都可以克服相位场的差异性，但并不能很好地兼顾算法的可靠性、效率和精确性等问题，所以在相位解缠的时候无论选择哪种算法都不能达到最优。直到Costantini等[16]于1996年提出网络规划的解缠算法，并利用网络规划算法妥善解决了上述问题，得到大家的认可和广泛应用。从图1可知,Delaunay MCF网络流算法消除了噪声这一影响因素，能够在含有比较严重的噪声干涉图中提取有用的数据。

2.3 不同阈值下的Delaunay MCF解缠

实验的第二部分则是在不同的阈值参数下针对Delaunay MCF进行研究。在将Delaunay MCF等级参数固定为1的情况下分别设置阈值0.01、0.1、0.2和0.5这4种情况，如图2所示。

图2 不同阈值的Delaunay MCF

由图2可知，从表面看来随着阈值的增加图中光亮点逐渐增加，黑暗点并无多大变化，当Delaunay MCF阈值设置为0.5时图中的亮点最多；当阈值更改为0.01时光亮点较为集中，数量相对较少；当Delaunay MCF的阈值设置为0.1时较为平滑。因此，阈值为0.1是Delaunay MCF较为适宜的阈值参数。

3 实验对比分析

3.1 解缠精度分析标准

不同的信噪比和信号将具有最佳或接近最佳的分解级别。分解级别对消除噪音的影响效果是巨大的，当分解等级过大时，对干涉图进行阈值处理会造成信号严重丢失。但是，噪声消除实际上会使信噪比降低，不仅如此还会导致运算量增大，进而使得处理变得缓慢;当分解级别太小时，去噪效果通常不尽人意，信噪比几乎没有改善，但信噪比并没有降低。

没有确定分解水平和阈值的固定经验或公式的情况下，通常只能通过对实验结果或信号特征进行反复测试，从而得到最优的结果。

3.2 解缠方法效率对比分析

相位解缠算法基本上是依靠解缠运行时间的速度和解缠精度的准确性作为解缠结果的评定标准。在相位解缠结束时如果所用的时间越长则解缠效率就越低，反之效率就越高。文中解缠精度准确性的高低是利用差值统计法，通过平均值和方差对比分析算法精度。

图3就是根据区域增长法、Delaunay MCF和最小二乘法绘制的统计图，从图中可以看出曲线普遍分布较好，且都较为光滑；Delaunay MCF和最小二乘法的零值较低，而区域增长法的零值过高。一般情况下，当零值过高时，认为数据在解缠的过程中存在一定的问题，可能是在中心区域存在较大的斑块，这种斑块会导致解缠不成功或者认定为解缠结果失败。

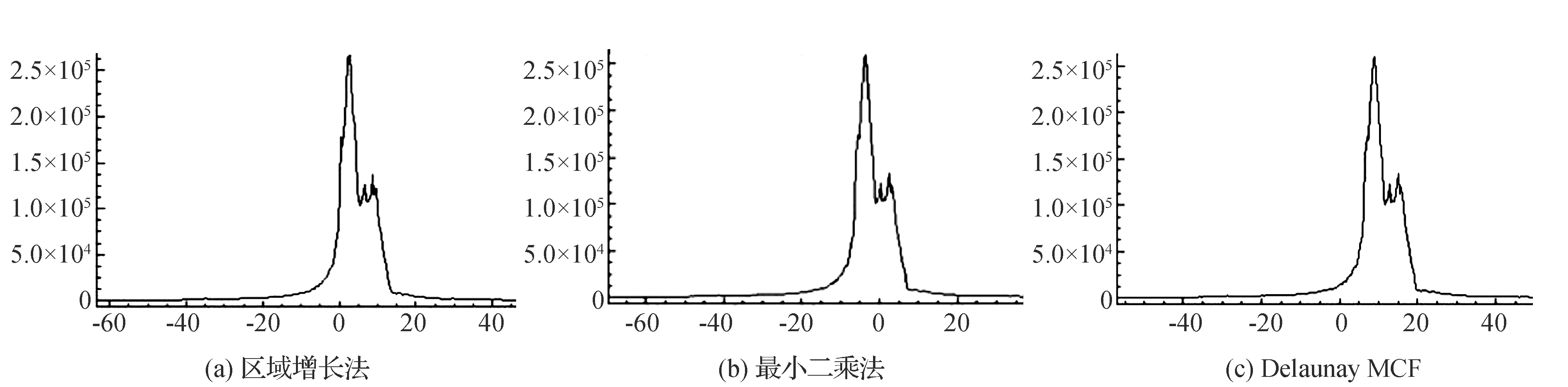
图3 3种解缠方法的统计结果

由于系统软件本身并没有计时功能，所以在此次实验中采用秒表计时。但由于操作时可能存在一定的误差，因此,采取多次计时求取平均值来减少误差。由表4可知，最小二乘法的解缠时间最快，而Delaunay MCF的解缠时间相对较少，区域增长法解缠所花费时间相对较多。

表4 3种算法解缠所用的时间

从表5可以看出,在0.01、0.1、0.2和0.5这4种阈值中的最小值基本一样，最大值、平均值和方差也没有多大的变化，但是随着阈值的增大可以发现最大值和平均值在逐渐减少，而方差则是先降低后增加。由于离散程度在数学中可以很好地评定一组数据的好坏，在一定程度上决定了相位解缠结果的偏差程度，因此，由表5中数据可知Delaunay MCF阈值在0.2是相对较为理想的阈值，离散程度也相对较小。

表5 Delaunay MCF在不同阈值时的比较

4 结束语

本实验主要通过对比不同的解缠算法来寻求适合低相干区的解缠算法，结果表明Delaunay MCF的准确性和解缠运行时间的效率较高。通过实验可以看出Delaunay MCF方法本质上来讲也属于路径追踪法，但与现在已经得知的任何路径追踪法又有所差异，因为三角网中只存在高质量的数据，消除了噪声这个对解缠结果有很大影响的因素，可以在含有比较严重的噪声干涉图中提取有用的数据。该方法可以有效地应用于低相干区域的解缠，提高干涉图的质量，为后续干涉处理提供更加可靠的数据。