同构法在高中数学题解析中的应用策略
秦波华,王勇强,吴利敏
(1.湖州市滨湖高级中学,浙江 湖州 313000;2.湖州市教育科学研究中心,浙江 湖州 313000; 3.湖州师范学院 理学院,浙江 湖州 313000)
数学中的同构不仅体现了数学的对称美与和谐美,而且运用同构法解题能够培养学生的化归思维能力.同构法是一种重要的思想方法和思维方式,在数学教学中有着非常重要的地位.但在当前的高中数学教学中,同构法的应用仍处于困境,因此有必要对其进行研究.本文在阐述同构的概念和同构法解题优势的基础上,探讨同构法在求解方程、不等式、数列、解析几何等方面的应用策略.
1 同构的概念与同构法的解题优势
在高中数学中,同构可定义为相同的结构.就表达式来说,可以定义为同构式,即除变量不同外,其余均相同的表达式;就方程来说,可以定义为同构方程,即除变量不同外,其余均相同的方程;就图像来说,可以定义为同构图像,即两个或两个以上的图形组合在一起共同构成一个新图形,这个新图形不是原图形的简单相加,而是一种对原图形的超越和突变.在高中数学教学实践中,很多问题都可通过寻找相同结构的表达式、方程和图形等来解决.如在恒成立求参数取值范围、证明不等式的过程中,同构法的运用不仅能够使学生理解和处理对象结构变得容易,还能使学者们对该领域有更深刻的理解[1].
2 同构法在高中数学题解析中的应用策略
2.1 集合中的“同构”定集合关系策略
例集合M={u|u=12m+8n+4l,m,n,l∈Z}与N={u|u=12p+16q+12r,p,q,r∈Z}的关系为____________.
应用策略本题是一道结构构造问题,可采用同构法构造20()+16()+12()与12()+8()+4(),只要()内是整数即可.
解决方案
u=12m+8n+4l= 12m+20l+20n-16l-12n= 20(n+l)+16(-l)+12(m-n),
其中,p=n+l、q=-l、r=m-n都是整数.同理,N⊆M.所以,M=N.
2.2 方程中的“同构”定参数值策略
例已知实数α、β分别满足α3-2α2+5α-17=0,β3-3β2+5β+11=0,求α+β的值.
应用策略两个方程都是3次方程,因此可采用同构法构造出f(x)=x3+2x-14,再证明函数在R上单调,且必与X轴相交,从而说明方程有唯一根.
解决方案由题意得(α3-3α2+3α-1)+2α-16=0,即得(α-1)3+2(α-1)-14=0,同理(β-1)3+2(β-1)-14=0,所以α-1、β-1都满足方程x3+2x-14=0.由f′(x)=3x2+2>0知f(x)=x3+2x-14单调递增,又f(0)=-14<0,f(3)=19>0,所以f(x)=0在R上只有一个实根(实质在区间(0,3)内有根),因此α-1=β-1,即α+β=2.
2.3 值域中的“同构”定参数范围策略
例若函数f(x)在定义域内存在区间[a,b],满足f(x)在[a,b]上的值域为[a,b],则称函数f(x)为“优美函数”.若函数f(x)=x2+k在(0,+∞)上为“优美函数”,则实数k的取值范围是____________.
应用策略如果方程f(a)=0与f(b)=0呈现同构特征,则a、b可视为方程f(x)=0的两个根.
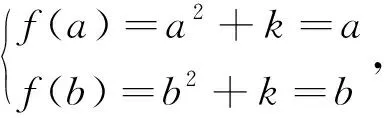
2.4 不等式中的“同构”定最值策略
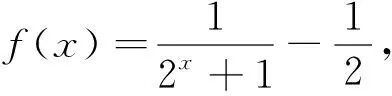
应用策略本题是解函数不等式,若采用直接代解析式,难度较大.此时常用的策略为:构造一个具有某些函数性质(如单调性、奇偶性)的函数,再利用函数的奇偶性和单调性解不等式.但此题还存在一个难点,即构造哪个函数.因此,应学会利用配凑或待定系数法去探求.
解决方案由已知得f(x+1-x2)-(x+1-x2)+f(x+2)-(x+2)<0,f(x+1-x2)-(x+1-x2)<-[f(x+2)-(x+2)].构造函数F(x)=f(x)-x,则F(x+1-x2)<-F(x+2).因此,可证明F(x)是奇函数.所以F(x+1-x2) 解决方案延长OG,交边AB于M,则M为AB的中点. (1) (2) 应用策略将递推公式变形为“依序同构”的特征,即关于(an,n)与(an-1,n-1)的同构式,从而将同构式设为辅助数列,以便于求解. 解决方案[3]由原式变形得: 记 则 (3) 例已知点P是y轴左侧(不含y轴)的一点,在抛物线C:y2=4x上存在不同的两点A、B,且满足PA、PB的中点均在C上.设AB中点为M,证明PM垂直于y轴. 应用策略为满足方程f(x1,y1)=0与方程f(x2,y2)=0,可构造同构方程f(x,y)=0,从而得出A(x1,y1)和B(x2,y2)都在曲线Ω:f(x,y)=0上.当方程f(x,y)=0是关于x、y的二元一次方程时,曲线Ω就是直线AB. 例已知函数f(x)=x2e3x.若x>0,恒有f(x)≥(k+3)x+2lnx+1,求实数k的取值范围. 同构是数学解题中的一项重要方法,它是数学本质最直接的体现.代数的根本在于运算和运算律,几何的根本在于空间的基本结构和基本性质.对核心问题的解析,唯有从构造入手,特别是从同构入手,才能真正揭示问题的核心[6].基础数学的本质是精简朴实的,其根源是自然直观的.在数学中,很多问题从表面看是纷繁芜杂的,但利用同构法可使它们变得简约明了.2.5 向量共线的“同构”两方面策略
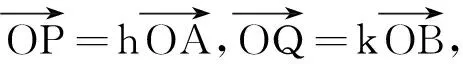

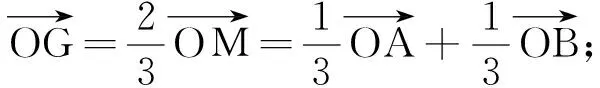

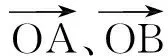
2.6 数列中的“同构”递推依序策略


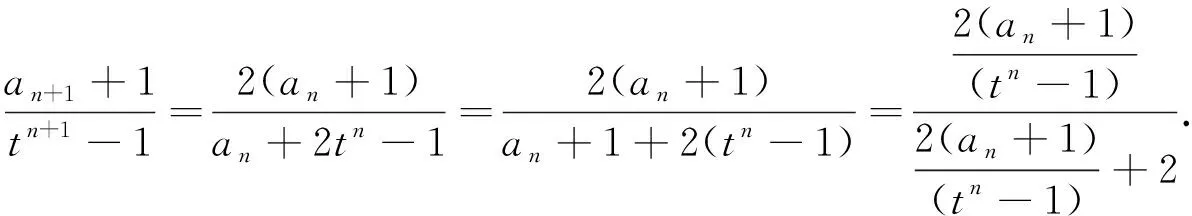
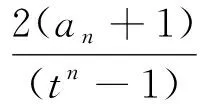

2.7 解析几何中的“同构”简化计算策略

2.8 导数中的指对跨阶“同构”策略

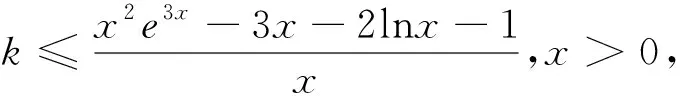
3 结 语

