MATLAB在均质土坝渗流计算中的应用

姚 震

(甘肃省水利水电勘测设计研究院有限责任公司，兰州 730030)

1 概 述

土石坝的渗流计算主要是为了确定坝体浸润线的位置，为坝体的稳定分析和布置观测设备提供依据；同时确定坝体与坝基的渗透流量，以便估算水库的渗漏损失，而且还要确定坝体和坝体渗流区的渗透坡降，检查产生渗透变形的可能性，以便采取适当的控制措施。在实用上，均质土坝渗流常采用分段法进行计算，而分段法需要求解非线性方程。Newton迭代法是解非线性方程最常用的方法，适用范围广泛，步骤简单。但如同所有的迭代法一样，它需要大量计算。MATLAB是一种强大的计算工具，利用MATLAB来实施Newton迭代法的计算可以大大节省时间[1]。本文以水平不透水层上均质土坝进行渗流计算。

2 渗流分析的水力学方法原理

2.1 水力学方法采用的基本假定

1) 坝体的材料为均质，且各点在各方向的渗透系数k相同。

2) 渗流为层流，认为渗透流速符合达西定律v=kJ。

3) 渗透水流是渐变流，认为任意过水断面上流速v相同。

2.2 计算简图

见图1。

图1 水平不透水层上均质土坝剖面图

图1中，H为坝高，m；b为坝顶宽，m；H1为坝前水深，m；H2为下游水深，m；hk为逸出点水深，m；a0为坝体下游逸出点距下游水面高度，m；ΔL为等效矩形体宽度，m；m1为上游坝面边坡系数；m2为下游坝面边坡系数；k为坝身的渗透系数，m/s。

2.3 水力学计算原理及过程[2]

在实用上，土石坝渗流计算常用分段法，并且又分为三段法和两段法两种。三段法是由巴甫洛夫斯基提出的，是将坝体内渗流区划分为3段，第一段为上游楔形段，第二段为中间段，第三段为下游楔形段。对每一段应用渐变流基本公式建立流量表达式，然后通过3段的联合求解，即可确定土石坝渗流量及逸出点水深，并可绘出浸润线。两段法是在三段法的基础上简化而来的，将上游楔形段和中间段合并，把土石坝渗流区划分成上游段和下游段两端。在下边的计算中，将用两段法来分析土石坝渗流。

在两段法中，把上游楔形段用假想的等效矩形体代替，即认为水流从垂直面渗入坝体，而矩形体宽度的确定，应使在相同的上游水深和单宽流量的作用下，分别通过矩形体和楔形体的水头损失相等。现用两断法来进行分析，根据实验研究，等效矩形体的宽度可由下式确定：

(1)

式中：m1为坝上游面的边坡系数。

2.3.1 上游段的计算

渗流从过水断面A′B′到CG的水头差ΔH=H1-hk，两过水断面之间平均渗透路程Δs=L+ΔL-m2hk。其中L=(H-H1)m1+b+Hm2，m2为坝下游坡面的边坡系数，故上游段的平均水力坡度为：

(2)

根据杜比公式，上游段的平均渗透流速为：

(3)

(4)

很显然，要用式(4)计算渗流量还不可能，因为逸出点水深hk是未知数，所以还必须要对下游建立计算公式，以便和式(4)进行联解。

2.3.2 下游段的计算

当下游水深H2≠0时，应将该段分为Ⅰ、Ⅱ两部分。第Ⅰ部分位于下游水面以上，为无压渗流；第Ⅱ部分位于下游水面以下，为有压渗流，近似认为下游段内流线为水平线。

下游段单宽总渗流量为：

(5)

式(5)中a0=hk-H2，联解方程式(4)、式(5)，可求得土石坝单宽渗流量q及逸出点高度a0。

2.3.3 浸润线计算原理及过程

因用等效的矩形体取代上游三角楔形体，A′B′即为上游的入渗起始断面，今取以G为坐标原点的一组直角坐标系来研究浸润曲线的计算，X轴以向左为正。浸润曲线的方程式为：

(6)

假定一系列x值，可由式(6)算得一系列相应的y值，点绘成浸润线。由式(3)所绘出的浸润曲线，其上游端是从A′点开始的，而实际上入渗点应在A，故曲线的前端A′F应加以修正。在实用上，常采用近似方法来修正它，即把A点作为曲线的上游端起点，再选择(用曲线板)适当能与后半段曲线光滑连接的曲线AF去代替A′F即可。见图1。

3 牛顿(Newton)迭代法原理[3]

Newton法是求解非线性方程最常用的方法，它是根据对非线性方程逐步线性化建立起来的一种迭代格式。

设非线性方程f(x)=0，且f连续可微，x*是方程的实根，x(0)是它的一个近似值。在x(0)附近将f线性化，即用f(x)在x(0)的一阶Taylor公式代替f(x)，得

f(x)≈f(x(0))+f′(x(0))(x-x(0))

(7)

则方程近似地表示为线性方程：

f(x(0))+f′(x(0))(x-x(0))=0

(8)

只要f′(x(0))≠0，可得新的近似根，记为x(1)，则：

(9)

一般地，设x(k)已经求出，在x(k)处将方程线性化：

f(x(k))+f′(x(k))(x-x(k))=0

(10)

若f′(x(k))≠0，式(10)有唯一解，记为x(k+1)，则得迭代格式：

(11)

式(11)称为Newton迭代格式。

Newton迭代法有明显的几何意义。因为方程f(x)=0的实根是曲线y=f(x)和X轴焦点的横坐标，而x(k+1)是曲线y=f(x)在点Pk(x(k)，f(x(k)))处的切线与X轴焦点的横坐标，因此迭代过程是逐次以切线代替曲线，用切线与X轴交点的横坐标x(k)逼近曲线与X轴交点的横坐标x*的过程。见图2。所以Newton法又称为切线法。

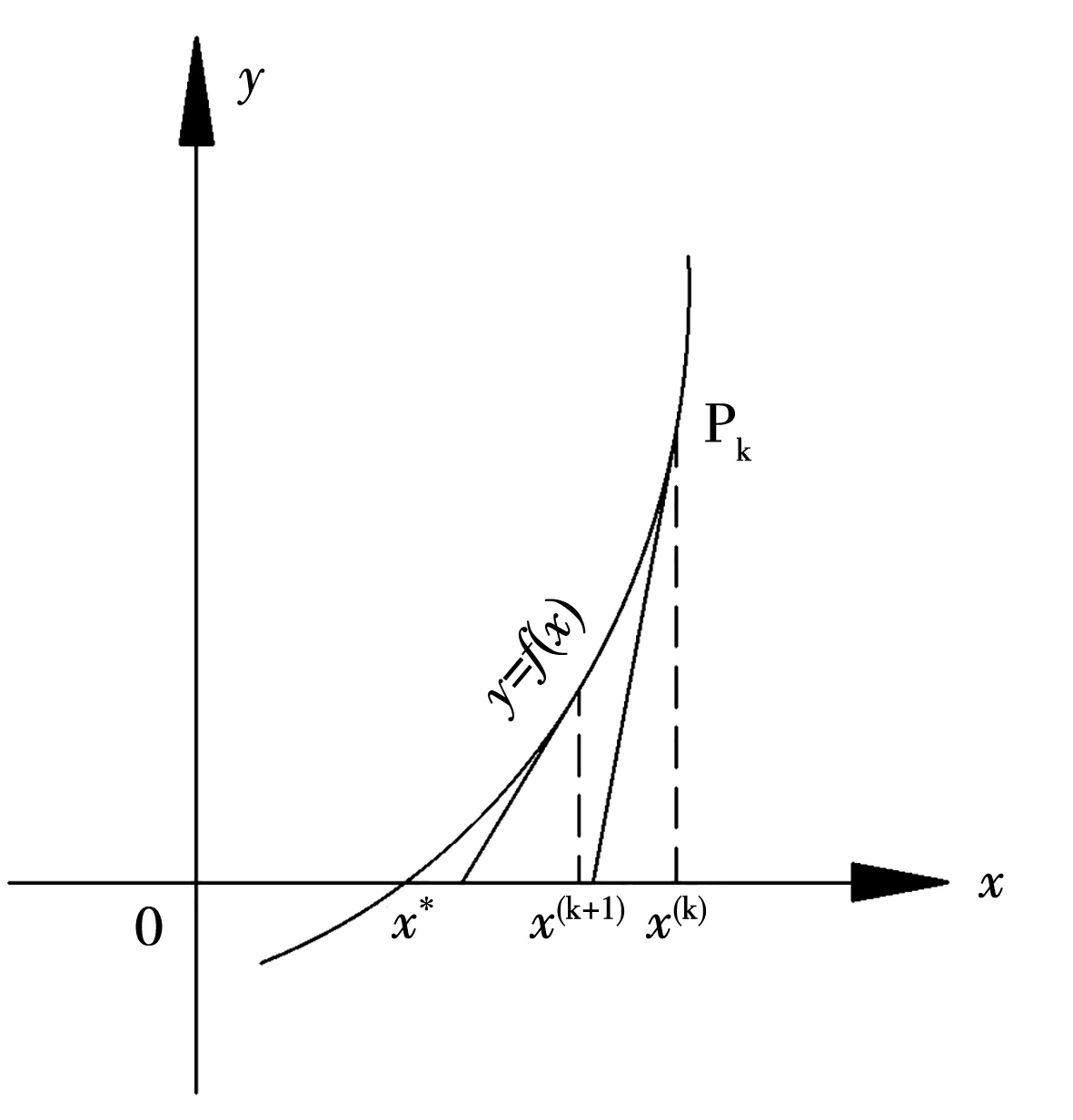
图2 Newton迭代法求根图示

4 用MATLAB实现某均质土坝的渗流计算

4.1 工程概况

某均质土坝建于不透水地基上，已知坝高H为17 m，上游水深H1为15 m，下游水深H2为2 m，上游边坡系数m1为3，下游边坡系数m2为2，坝顶宽b为6 m，坝身土的渗透系数k经实验测得为0.001 cm/s。

4.2 用MATLAB实现渗流计算

%水平不透水层上均质土坝渗流计算

%1、输入已知参数

H=17;

b=6;

H1=15;

H2=2;

m1=3;

m2=2;

k=0.00001;

%2、水力学法渗流计算过程

%2.1、上游段

%等效矩形体宽度

ΔL=(m1./(1+2.*m1)).*H1；

L=(H-H1).*m1+b+H.*m2；

%(1)q=k.*((H1.^2-(H2+a0).^2)./(2.*(L+ΔL-m2.*(H2+a0))))；

%2.2、下游段

%(2)q=(k.*a0./m2).*(1+2.3.*log10((H2+a0)./a0))；

%联立(1)、(2)可得下式

% k.*((H1.^2-(H2+a0).^2)./(2.*(L+ΔL-m2.*(H2+a0))))…

% =(k.*a0./m2).*(1+2.3.*log10((H2+a0)./a0))

%3、用牛顿迭代法求解渗流量

%3.1、m文件定义函数

function y=fun1(a0，k，H1，H2，L，ΔL，m2)

y= k.*((H1.^2-(H2+a0).^2)./(2.*(L+ΔL-m2.*(H2+a0))))…

-(k.*a0./m2).*(1+2.3.*log10((H2+a0)./a0))；

end

function Y=fun2(a0，k，H1，H2，L，ΔL，m2)

Y=a0-fun1(a0，k，H1，H2，L，ΔL，m2)./ diff(fun1(a0，k，H1，H2，L，ΔL，m2))；

end

%3.2、选定初始值

a0=0:0.000001:5；

y=fun1(a0，k，H1，H2，L，ΔL，m2)；

plot(a0，y)；

grid on；

%3.3、求出迭代函数

syms a0

%Y=a0-y./ diff(y)；

Y=fun2(a0，k，H1，H2，L，ΔL，m2)；

%3.4、实施迭代

%等价方程：a0=Y

a0=3；

i=1;

while i<=10

a0+1=subs(Y，a0)；

if (abs(a0+1-a0)>1e-5)

a0=a0+1；

else break

end

i=i+1；

end

fprintf(’a0=%f’，a0)

%3.5、求出单宽渗流量

q=(k.*a0./m2).*(1+2.3.*log10((H2+a0)./a0))

%4、绘制浸润线

x=[0：5：L+ΔL-m2.*(a0+H2)，L+ΔL-m2.*(a0+H2)]

y=sqrt((x./(L+ΔL-m2.*(H2+a0))).*(H1.^2-(H2+a0).^2)+(H2+a0).^2)

运行程序，输出结果：

a0=3.162856

q=2.36e-005

x=0 5.0000 10.0000 15.0000 20.0000 25.0000 30.0000 35.0000 40.0000 42.1029

y=5.1629 7.0859 8.5886 9.8651 10.9943 12.0179 12.9609 13.8398 14.6661 15.0000

5 与理正岩土渗流分析软件计算成果的比较分析及建议

5.1 理正岩土渗流分析软件计算成果

将上述工程计算参数输入理正岩土渗流分析软件渗流问题公式法模块，计算结果整理如下：

下游出逸点高度：a0=3.993(m)

单位宽度渗流量：q=2.34×10-5(m3/s·m)

5.2 计算成果比较分析及建议

比较本文水力学计算成果和理正岩土渗流分析软件计算成果，前者下游出逸点高度为3.163 m，后者为3.993 m；前者单位宽度渗流量为2.36×10-5m3/s·m，后者为2.34×10-5m3/s·m。造成两种计算方法下游出逸点高度差值较大的原因是：本文采用水力学渗流计算公式，理正岩土渗流分析软件依据《堤防工程设计规范》(GB 50286-2013)不透水堤基均质土堤渗流计算公式[7]，两种公式计算结果有差异。

依据《碾压式土石坝设计规范》(SL 274-2001)，贴坡排水顶部高程应高于坝体浸润线出逸点[8]。理正岩土渗流分析软件计算的出逸点高度较本文水力学渗流计算公式高，相应贴坡排水顶部高程也较高，理正计算结果对于工程来说更加保守。

6 结 语

本文结合实例，阐述了水平不透水层上均质土坝的渗流计算，可以看出利用MATLAB来实施Newton迭代法可以大大节省时间。MATLAB渗流计算程序具有通用性，对其它工程均质土坝渗流计算具有参考意义。通过分析比较本文水力学渗流计算成果和理正岩土渗流分析软件计算成果可知，理正计算结果对于工程来说更加保守。