中山市水资源系统动态模拟与敏感性分析

关雪桦,陈志和,叶智恒

(1.中山大学土木工程学院，广东 珠海 519082; 2.中山大学地理科学与规划学院，广东 广州 510275)

水是维持区域社会经济可持续发展的重要资源，亦是区域自然生态系统良性循环的控制性要素[1]。随着人口的增长与经济的发展，水资源短缺、水环境恶化的问题愈发突出[2-3]，严重制约着区域经济社会发展。如何实现水资源的开发利用与经济社会的协调发展已成为研究热点[4]。目前，已有学者从不同角度开展了水资源开发利用与经济社会发展耦合研究，为制定区域发展战略与实施规划提供了科学依据。李敏等[5]模拟分析了云南省水价、水利技术等条件的变化对经济社会的影响，指出缓解水资源供需矛盾的方法；卢超等[6]探究了水资源承载力约束下小城镇经济变化的趋势，提出构建节水型社会的建议；Kotir等[7]建立了系统动力学(system dynamics， SD)模型以探索水资源与农业生产之间的相互作用；焦士兴等[8]分析了河南省各市城镇化与水资源系统的协调发展状况,为提高城市发展质量提供了新思路。然而，传统的研究多为评估特定情景下区域水资源系统的变化趋势，但由于情景的设计往往基于经验估计，且特定情景存在可操作性不强的问题[9]，导致了水资源管理方案的实施效果不佳。对水资源系统进行敏感性分析以识别关键参数是制定有效管理政策的重要步骤，对实现协调可持续发展具有现实指导意义[10]。

本文运用SD理论，综合经济社会、水质、水量等要素构建SD模型，以中山市为例，模拟快速发展背景下水资源系统的变化趋势，并在此基础上采用熵权TOPSIS(technique for order preference by similarity to an ideal solution)模型对水资源系统进行敏感性分析，寻找对水质、水量以及经济社会综合影响最深的参数，以期为区域水资源管理者决策提供参考。

1 研究区概况与数据来源

1.1 研究区概况

中山市位于广东省中南部，处于粤港澳大湾区的中心地带，全境位于东经113°09′～113°46′、北纬22°11′～22°47′，总面积为1 800.14 km2。2000年以来，中山市形成了有较强竞争力的产业链和产业群，经济社会持续快速发展。2018年，中山市地区生产总值为3 632.7亿元，同比增长5.9%；常住人口331万人，同比增长0.962%；城镇化率为88.35%。

中山市属亚热带季风气候，雨量充沛，水资源量丰富，多年平均降水量为1 710.3 mm，平均水资源总量17.38亿m3(不含过境水)，多年平均入境水与过境水资源量分别为2 662.94亿m3和2 678.92亿m3。中山市现供水能力为168 619万m3/a，但其水资源主要依赖上游过境水量，且市内蓄水工程少，调蓄能力不强，应对污染事故等突发事件和水质性缺水状况的能力受到限制。在水质方面，根据2018年水质监测成果，中山市主要大江大河水质较好，但城市内河石岐河水质不达标(劣Ⅴ类)，主要是溶解氧、氨氮超标；长江水库为Ⅲ类水质，超标项目为总氮。

1.2 数据来源

本研究使用的人口、GDP、三产比例等社会经济数据来源于2005—2018年《中山市统计年鉴》；用水量、需水量、用水定额等数据则来源于2005—2018年《中山市水资源公报》；GDP、人口预期增长率、产业比例目标以及城镇化率目标根据国民经济规划、城市总体规划综合确定：中山市2020年和2030年GDP预期增长率分别为7.7%和5.0%，第一、二、三产业比例目标分别为1.6∶46.1∶52.3和1.2∶43.8∶55.0，人口预期增长率均为1.0%，城镇化率目标分别为89.13%和91.0%。

2 研究方法

2.1 中山市水资源SD模型

SD模型设定模拟时间为2005—2040年，其中2005—2018年作为模型验证，基准年为2005年，时间间隔为1 a。

2.1.1因果关系图建立

在建模过程中，根据对系统的分析结果，确定系统内部主要变量之间的反馈关系[11]，见图1。其中，蓝线代表同向影响，如农业需水量的增加将导致需水总量的增加；红线代表反向影响，如污染物入河量的增加将导致水环境容量余量减少。

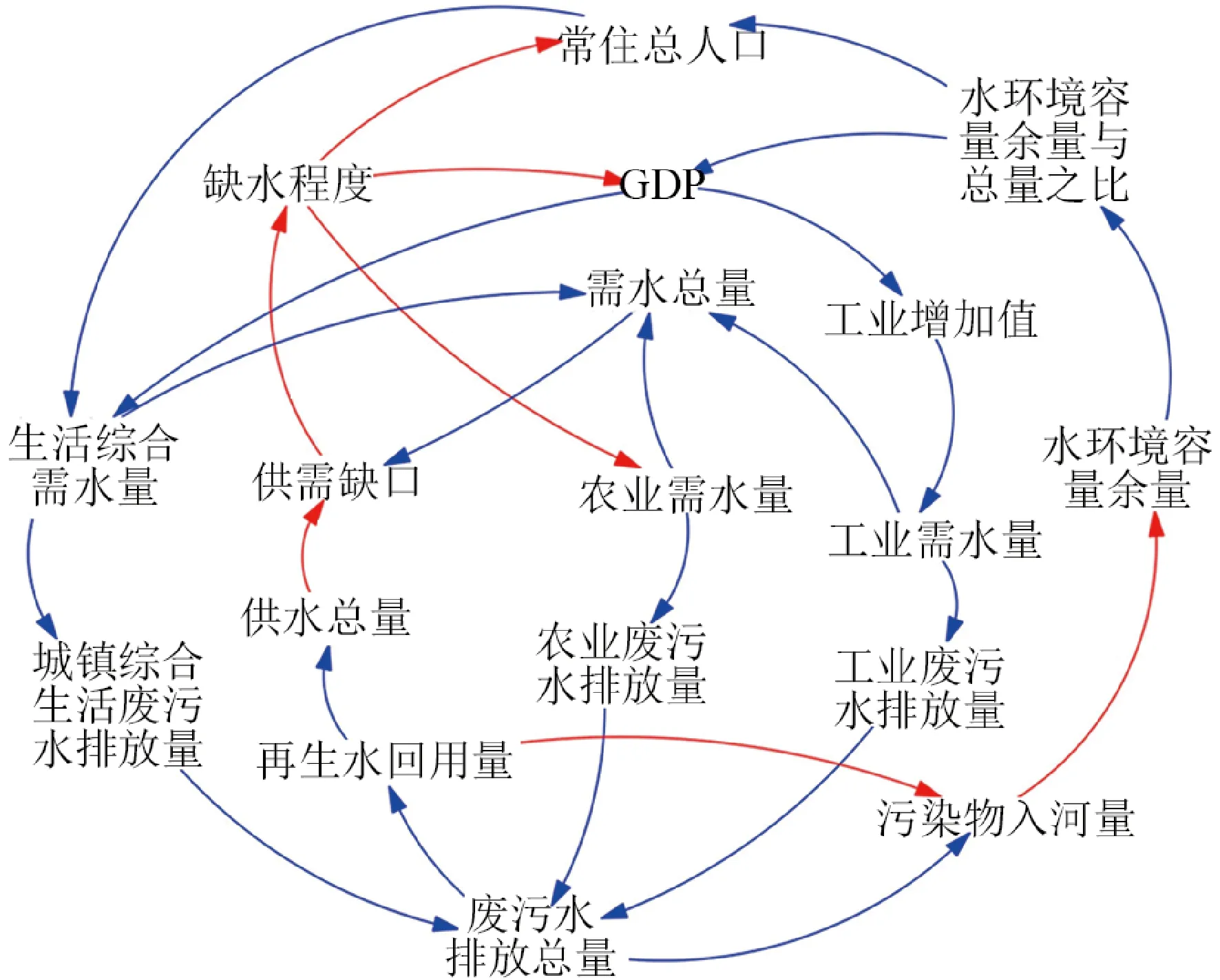
图1 主要变量的反馈关系

2.1.2模型结构划分及系统流图

结合收集到的相关信息以及中山市的实际情况，将中山市水资源系统划分为6个子系统。6个子系统彼此相对独立，但是在整个大系统中密不可分。运用SD专用建模软件Vensim-DSS构建了中山市水资源SD模型，其系统流图如图2所示。图2中状态变量是随时间变化的积累量；速率变量是表示累积效应变化快慢的变量；影子变量是绘图时调用的模型中另一子系统已定义的变量；〈Time〉为时间变量，用于确定变量与时间的表函数;其他辅助变量是系统中的信息量。

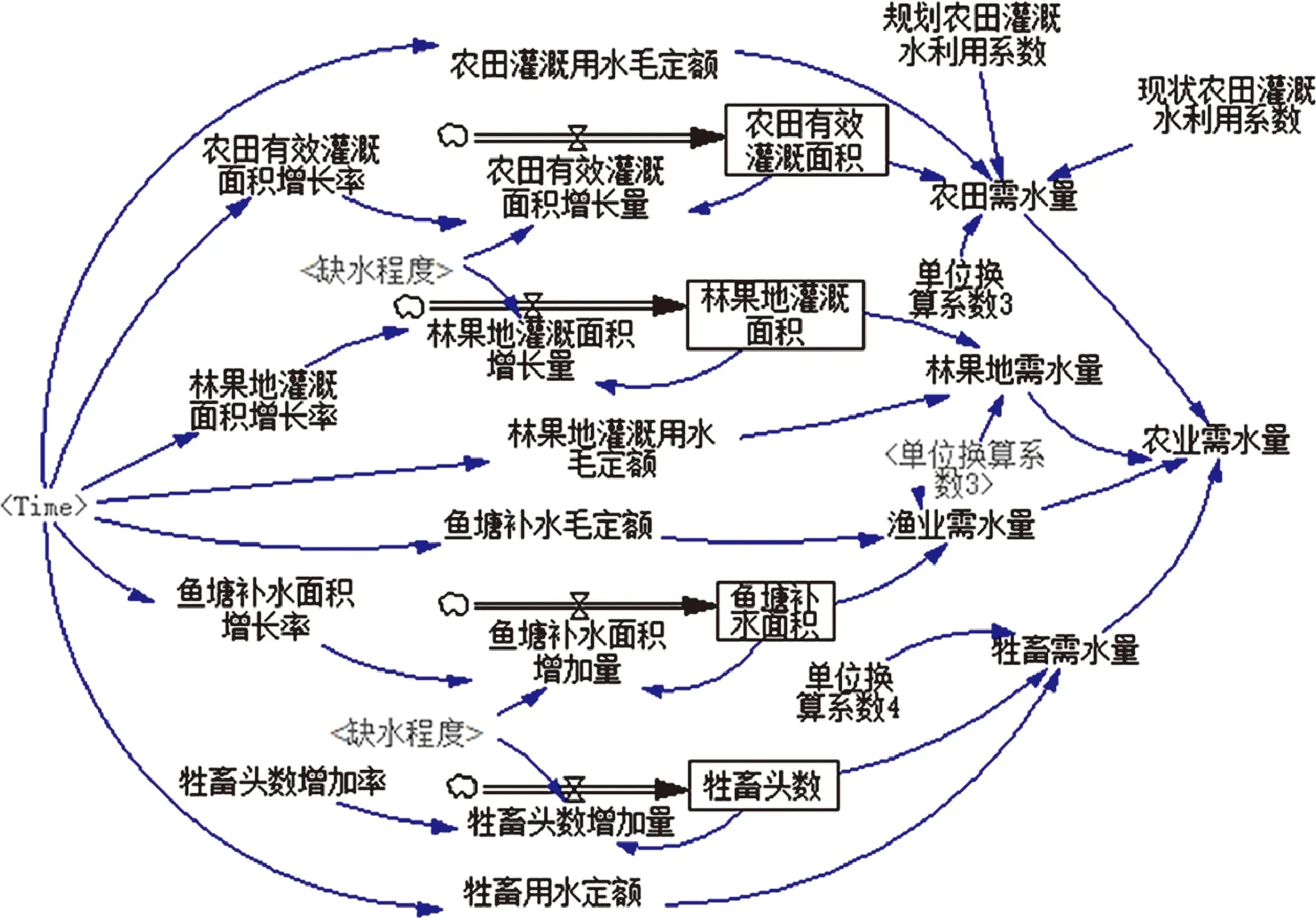
(a) 农业需水子系统

a.农业需水子系统。农业需水包括农田灌溉需水、林果地灌溉需水、鱼塘补水和牲畜需水。本文根据历史数据分析农田灌溉用水毛定额、林果地灌溉用水毛定额、鱼塘补水毛定额和牲畜用水毛定额，结合全市农田有效灌溉面积、林果灌溉地面积、鱼塘补水面积、牲畜头数等，采用用水定额法计算求得农业需水量。

b.废污水子系统。中山市的废污水主要来源于城镇综合生活废污水、工业废污水和农业废污水。

c.生活综合需水子系统。生活综合需水量包括城镇生活需水量、农村生活需水量、城镇公共需水量和城镇生态环境需水量。前两者主要采用人均日用水定额方法求得，城镇公共需水量和城镇生态环境需水量则分别采用万元产业增加值用水定额法、面积定额法计算求得。

d.水资源供需子系统。中山市供水主要来源于地表水和地下水，同时利用雨水、咸淡水和再生水以供给非生活综合需水的其他方面需水。

e.工业需水子系统。工业需水量包括一般工业需水量和火核电冷却需水量。其中火核电冷却需水量通过表函数形式表示；一般工业需水量则采用用水定额法计算；根据历史数据分析中山市万元工业(不含火电)增加值用水量的变化趋势，结合一般工业增加值的计算，得到一般工业需水量。

f.水环境子系统。考虑指标的代表性与可得性，本文研究的污染物为氨氮和化学需氧量(COD)。城镇综合生活和工业产生的污染物入河量根据城镇综合生活和工业废污水的排放量，结合处理率、达标率、处理前后的排放浓度等指标求得；对农田污染物采用源强系数计算方法，对牲畜养殖业通过排水系数、排放浓度等指标计算其入河污染物。

模型涉及的主要方程如下：

a.供水总量为

(1)

式中：ST为供水总量，m3；LS为用水总量限制标准，m3；CS常规供水能力，m3。

b.一般工业需水量为

DGI=DAIAI

(2)

式中：DGI为一般工业需水量，m3；DAI为万元工业(不含火电)增加值用水量，m3/万元；AI为一般工业增加值，万元。

c.工业需水量为

DI=DGI(1-RPR+RCR)-DIN(RC-RP)+DTP

(3)

式中：DI为工业需水量，m3；RPR为规划工业用水重复利用率，%；RCR为现状工业用水重复利用率，%；DIN为非自备水源工业取水量，m3；RC为现状管网综合漏失率,%；RP为规划管网综合漏失率，%；DTP为火核电冷却需水量，m3。

d.农业需水量为

DA=DC+DW+DF+DL

(4)

式中：DA为农业需水量，m3；DC为农田需水量，m3；DW为林果地需水量，m3；DF为渔业需水量，m3；DL为牲畜需水量，m3。

e.生活综合需水量为

DD=DAD+(DUD+DUP)(1-RC+RP)+DUE

(5)

式中：DD为生活综合需水量，m3；DAD为农村生活需水量，m3；DUD为城镇生活需水量，m3；DUP为城镇公共需水量，m3；DUE为城镇生态环境需水量，m3。

f.需水总量为

DT=DA+DI+DD-DR

(6)

式中：DT为需水总量，m3；DR为非常规水资源开发利用量，m3。

g.氨氮总入河量为

WTNH3-N=WANH3-N+WUNH3-N+WINH3-N-WRNH3-N

(7)

式中：WTNH3-N为氨氮总入河量，t；WANH3-N为农业产生的氨氮入河量，t；WUNH3-N为城镇生活产生的氨氮入河量，t；WINH3-N为工业产生的氨氮入河量，t；WRNH3-N为再生水回用减少的氨氮入河量，t。

h.COD总入河量为

WTCOD=WACOD+WUCOD+WICOD-WRCOD

(8)

式中：WTCOD为COD总入河量，t；WACOD为农业产生的COD入河量，t；WUCOD为城镇生活产生的COD入河量，t；WICOD为工业产生的COD入河量，t；WRCOD为再生水回用减少的COD入河量，t。

2.1.3模型参数的取值

模型2018年主要参数取值为：咸淡水再生水利用量、火核电冷却需水量分别为24 112万m3和 6 800万m3，万元工业(不含火电)增加值用水量、城镇公共用水定额分别为19 m3/万元和8.46 m3/万元，城镇生活污水处理率、规划管网综合漏失率、规划工业用水重复利用率分别为85%、12.18%和26.39%，农村人均用水定额、城镇人均用水定额分别为136 L/d和165 L/d,污水处理厂COD排放质量浓度、氨氮排放质量浓度分别为60 mg/L和8 mg/L，牲畜用水定额为11.26 L/(d·头)，环卫用水定额为2.1 L/(m2·d)，农田灌溉用水毛定额、林果地灌溉用水毛定额、鱼塘补水毛定额分别为10 680.00 m3/hm2、4 222.95 m3/hm2和9 726.60 m3/hm2。

2.1.4模型验证

为了验证模型的运行结果是否符合实际情况，对模型进行历史性检验。对比分析中山市2005—2018年模型模拟结果与实际数据(表1)可知：在所选取的变量中，生活综合需水量模拟值的相对误差较大，但超过10%的年份较少，其他变量模拟值的相对误差都在10%以下，大部分在5%以内。总的来说，模型的模拟结果有效地反映了实际情况，具有较高的可信度。

2.2 熵权TOPSIS评价模型的构建

2.2.1指标体系的选取

保护资源与环境是可持续发展的前提，为促进水资源开发利用与经济社会的协调发展，本文选取了水资源供需比、COD水环境承载系数、氨氮水环境承载系数和GDP作为评价指标。其中，水资源供需比为实际可供水量与经济社会发展需水量的比值，实际可供水量根据最严格水资源管理制度中用水总量限制标准确定；COD和氨氮水环境承载系数分别为COD和氨氮水环境容量与污染物入河量的比值。该指标评价体系遵循了系统性原则，表征了资源利用目标、环境目标以及经济目标3个层面[12-13]，具有一定的代表性。

2.2.2评价方法

TOPSIS法是根据评价对象与理想方案的接近程度进行排序的评价方法，具有计算过程灵活方便、评价结果合理等优点[14-15]，而熵权法是根据指标原始数据确定权重的一种客观赋值方法，将其与TOPSIS法结合，可克服TOPSIS进行评价具有主观性这一缺点[16-17]，能够客观评价不同方案对中山市水资源系统的影响。

熵权法的主要计算步骤为：

步骤1假定有m个评价对象，每个评价对象有n个评价指标，利用评价对象的不同评价指标的实测值构造判断矩阵。

步骤2将实测值构成的判断矩阵进行归一化处理，正向和负向指标归一化公式分别为

(9)

(10)

式中:xij为评价对象i的评价指标j的实测值；xjmax、xjmin分别为评价指标j对应的不同评价对象的最满意与最不满意的值。

步骤3计算各评价指标的熵值：

(11)

其中

(12)

式中Hj为评价指标j的熵值。

步骤4计算各评价指标的权重：

(13)

式中wj为评价指标j的权重。

TOPSIS模型综合评价法的主要计算步骤为：

步骤1数据同趋势化与无量纲化。通过反比将负向指标数据正向化，将正向化处理后的数据按下式进行无量纲化处理，即得到无量纲决策矩阵Z=(zij)m×n：

(14)

式中vij为正向化后评价对象i的评价指标j的值。

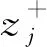
(15)

(16)

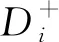
(17)

(18)

步骤4确定接近度Ci：

(19)

Ci值越接近于1说明该对象与最佳方案越靠近，即对象相对最优，最终按各对象接近度大小进行排序。

3 结果与分析

3.1 常规发展模式模拟

常规发展模式，即假定中山市维持现状供用水水平、节水强度和污水治理力度等，经济社会指标按照现行的城市总体布局和发展规划确定，不采取任何水资源管理措施的发展模式。在Vensim-DSS中运行所建立的中山市水资源SD模型，模拟常规发展模式下中山市2019—2040年的水资源供需、经济社会以及水环境状况的变化趋势，结果如图3所示。

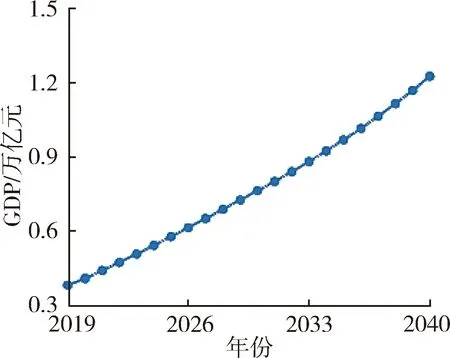
(a) GDP

在常规发展模式下，中山市未来的GDP将持续增长，2020年、2030年和2040年GDP分别为 4 093.43亿元、7 631.64亿元和12 237.70亿元；2020—2030年、2030—2040年GDP年均增长率分别为6.43%、4.84%，发展速度逐步放缓。中山市的需水总量持续增加，到2034年需水总量将达到14.93亿m3，届时将超过中山市供水总量，缺水量为0.42亿m3；到2040年，缺水量将达到4.02亿m3，水资源供需比仅为0.78。中山市的水环境承载系数将持续下降，2035年，中山市将出现COD水环境容量不足现象，COD水环境承载系数为0.98，至2040年，COD水环境承载系数将下降至0.80；氨氮污染则更为严重，2020年氨氮入河量为3 869 t，已超过中山市氨氮水环境容量315 t，且随着时间的推移，污染愈发严重，2030年和2040年氨氮水环境承载系数仅为0.57和0.38。

3.2 敏感性分析

在常规发展模式下，中山市的水资源问题愈发突出，将影响中山市的可持续发展，亟须制定水资源管理方案。为寻找对水资源系统影响显著的参数，为水资源管理提供方向，本文设计不同方案对水资源系统进行敏感性分析。

3.2.1方案设计及模拟结果分析

根据最严格水资源管理制度设立的目标及不同学者对华南河网地区水资源问题的研究[18]，本文初步设计了12个方案进行参数敏感性分析。方案设计的基本思路为：在常规发展模式的基础上，每个参数2030年的具体数值向有利于水资源系统发展的方向改变10%，且每次只变动1个参数。所选方案涵盖了水量调整与水质管控两个方面，且参数变化范围不大，具有一定的代表性与可行性。运行所建立的SD模型，得到不同方案下目标变量的变动情况。方案的具体设计及模拟结果如表2所示。

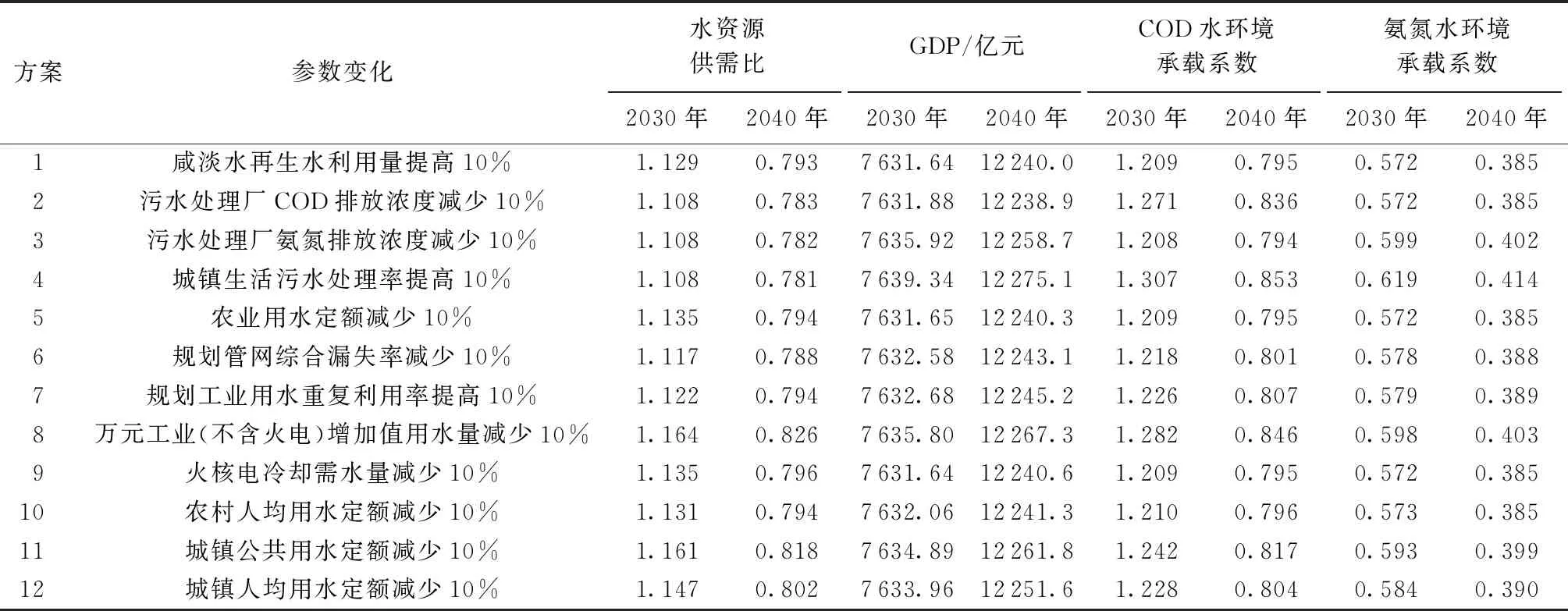
表2 方案设计及目标变量模拟结果

在缓解水资源供需矛盾方面，方案8取得最优效果，2030年和2040年水资源供需比较常规发展模式分别提高4.9%和5.5%。在促进GDP增长方面，方案4为最优方案，2030年和2040年GDP分别达到7 639.34亿元和12 275.1亿元，较常规发展模式分别增加7.7亿元和37.4亿元。在改善水质方面，方案4能同时提高了COD与氨氮水环境承载系数，是最有利于改善水环境质量的方案；而方案2和方案3仅能提高COD和氨氮水环境承载系数中的一个指标，不能系统地改善水环境质量。

3.2.2熵权法TOPSIS模型综合评价结果分析

由以上分析可知，同一方案能对其中个别指标产生明显作用而对另外指标影响较小。为衡量不同参数变化对整个水资源系统的影响，本文运用熵权TOPSIS模型进行综合评价并排序，从而得出优选方案。

根据中山市2005—2018年历史数据，利用熵权法对所选指标赋权。赋权结果为：水资源供需比、COD水环境承载系数、氨氮水环境承载系数、GDP的权重分别为0.338、0.239、0.227、0.196。在所构建的指标体系中，水资源供需比所占权重最大，水环境承载系数次之，而经济社会所占权重最少，赋权结果与珠江三角洲其他城市水资源承载力计算中指标赋权的结果相近[19-20]，是合理且可靠的。

利用熵权TOPSIS模型对方案进行综合评价。分别计算2030年和2040年各方案与最优解的接近度，根据接近度进行排序，如表3所示。

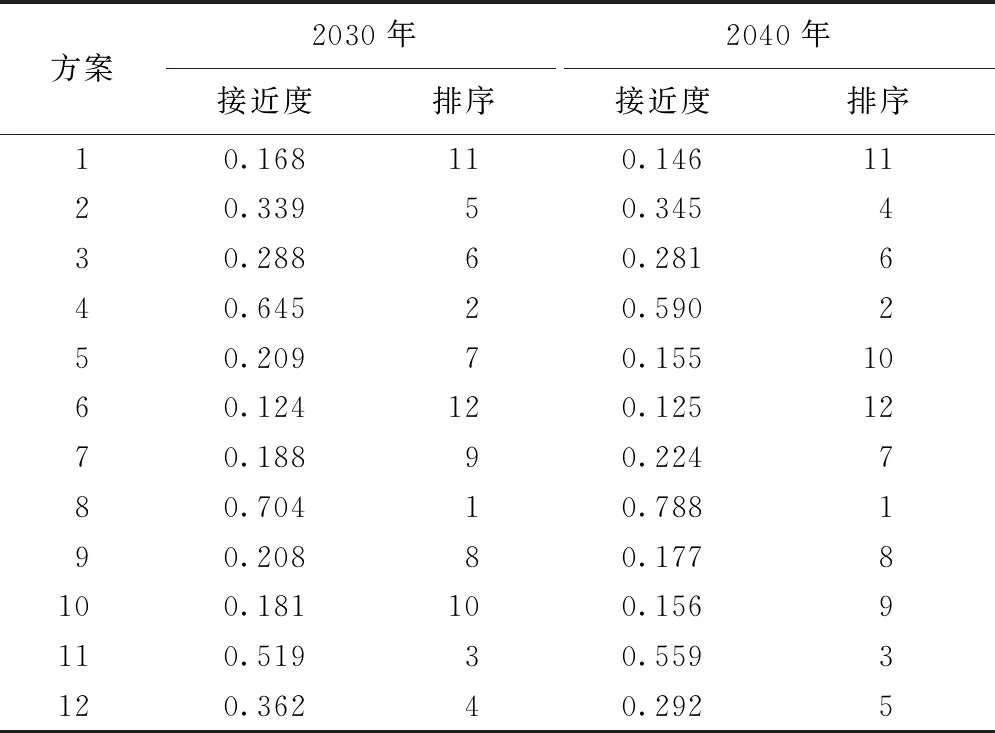
表3 方案综合评价结果

根据2030年综合评价结果，方案8对中山市水资源系统的综合影响最大，为所有方案中的最优方案。方案8能有效促进工业节水，在减少需水量的同时减少相应的污染物排放量，延缓水环境恶化；而水资源供需矛盾减缓、水环境的改善又将作用于经济社会系统，促使GDP增速提高。方案8对4个指标的改善均发挥明显作用，故对整个水资源系统产生显著影响，适用于调整中山市水资源管理政策。方案4能减少入河污染物的排放，有效改善水环境质量且促进GDP的增长，但该参数的调节对水量影响甚少，故对综合指标的影响低于方案8。方案11与方案12调整了城镇用水量，在减少用水量的同时也减少了污染物的排放，GDP增长速度也有所提高。从上述分析可以看出，控制用水量更容易促使系统达到全面平衡的状态，但控制不同部门的用水也会得到不同的效果，如方案5对系统的综合影响劣于方案8和方案11。

对比2030年和2040年的排序结果，12个调整方案对近、远期的影响程度有一定的区别。如方案5在2030年和2040年排名分别为第7和第10，表明减少农业用水定额对水资源系统近期影响较大，但随着时间的推移，其影响将会有所降低；方案7的效果则相反，表明工业用水重复利用率的提高对近期的影响较小，但随着时间推移，其影响会更加显著。2030年和2040年排在前50%的方案大体相同，但为了使水资源管理政策更加适合长远的发展，需重视远期作用更加明显的参数调整方案，如工业用水重复利用率的提高。水资源的管理不仅应着眼于当下，更应放眼未来，从而促使城市可持续发展。

4 结 论

a.常规发展模式下，中山市水资源供需矛盾逐渐凸显，水环境恶化愈发严重。

b.万元工业(不含火电)增加值用水量的减少对水资源系统的影响最大，相应的方案适用于调整中山市水资源管理政策。

c.控制用水量更容易促使水资源系统达到全面平衡的状态，有助于实现经济社会的可持续发展。

d.不同方案对近期及远期的影响不尽相同，为了使水资源管理政策更适合长远的发展，决策者应重视远期作用更为明显的参数调整方案。