基于机器学习的山洪灾害快速预报方法
周 聂,侯精明,陈光照,马红丽,洪增林,李新林
(1.西安理工大学省部共建西北旱区生态水利国家重点实验室,陕西 西安 710048;2.鄂尔多斯市水利勘测设计院,内蒙古 鄂尔多斯 017000; 3.陕西省地质调查院,陕西 西安 710054)
山洪指在山区溪沟中由于强降雨等原因引起水位短时间内暴涨形成的洪水,具有流速大、冲刷力强、破坏力强等特点,通常会给交通、农业、居民生命财产安全等造成巨大威胁[1]。据《2017年中国生态环境状况公报》统计,2017年洪涝灾害累计受灾人口5 515万人,因灾直接造成经济损失达2 143亿元[2]。随着全球气候变化,极端降雨事件频率增大,2018年全国累计454条河流出现超过警戒水位的洪水,其中24条河流发生超历史洪水[3]。由于山洪灾害具有突发性及破坏性特点,如何应对山洪灾害,降低损失,一直以来都是国内外学者研究的热点与难点。
山洪灾害模拟预报能够有效模拟山洪灾害的受灾范围,为山洪风险管理、应急决策提供依据,是协助防灾减灾工作的重要方式之一。众多学者对此进行了研究,包红军等[4]基于新安江模型开发了分布式混合水文模型,模型预报精度较高;胡国华等[5]用HEC-HMS半分布式水文模型进行山洪模拟,洪峰流量及洪量相对误差可控制在20%以内;孟天翔[6]基于MIKE FLOOD构建水动力模型开展山洪数值模拟,获得各类洪水淹没演进变化情况。然而传统山洪模拟研究都有一个共同的缺陷,即需要求解复杂的方程组,按步时顺序迭代以获取洪水的演进过程,模拟运算耗时长,无法满足紧急决策的需求。近年来,随着人工智能技术的发展,机器学习技术以其普适性与高效性,在医学、化学、数据挖掘等领域都得到了广泛应用并展现出突出优势[7-9],国内外学者也逐渐将人工神经网络、逻辑回归、极限树回归等机器学习算法应用于洪涝灾害的预测中[10-12]。阚光远等[13]将ANN与KNN方法相耦合,提高了ANN预报能力不佳等问题;张珂等[14]将洪水预报智能模型应用于中国半干旱半湿润地区,所建模型在半湿润区典型流域可获得良好的预报结果;张轩等[15]基于BP神经网络算法建立经验预报,模型预报精度可达乙级以上;Chang等[16]基于ANN构建了洪水淹没多步预测模型;Fauzi等[17]同样基于机器学习算法构建了海啸淹没的预报模型。这些研究表明,机器学习技术在洪水预报方面同样具有广阔的应用前景。
机器学习往往需要大量的训练数据,目前洪水灾害快速预报多基于水文站多年的实测数据,依靠完备的大数据进行训练,但对于未发生过洪水或历史淹没资料匮乏的地区无法进行有效预测。为此,本文基于高精度水动力模型与机器学习技术,选取王茂沟流域为研究区域,以数值模型模拟数据作为驱动数据,探索构建实测洪水资料匮乏流域的山洪灾害快速预报模型,旨在为紧急决策提供足够的前置时间,协助决策者更好地采取应对措施。
1 研究区概况与降雨资料
1.1 研究区概况
本文选取陕西省榆林市绥德县的王茂沟流域作为研究区域,该流域位于东经110°20′26″~110°22′46″,北纬37°34′13″~37°36′03″,总面积约为5.74 km2,王茂沟主沟长3.75 km,沟道平均比降为2.7%。流域海拔高度介于940~1 200 m,属温带半干旱大陆性季风气候,历史最大年降水量为735.3 mm,多年平均降水量为475.1 mm,7—9月降水量可达全年降雨的64%,且多为短历时强降雨,极易引起山洪、泥石流等灾害。2012年7月15日及2017年7月26日均出现高强度暴雨,形成山洪,造成巨大经济损失[18-19]。
地形精度对数值模拟至关重要,精度不足将无法反映实际地形特征,影响模拟的可靠性;精度过高对模拟精确性提高不大,但会严重延长模型的运行时间。经综合考虑,将研究区域以5 m的水平分辨率划分为232 037个网格,其数字高程图见图1,土地利用情况见图2。同时,为更好地表征下垫面信息,将研究区根据不同的土地利用类型,基于最大似然法划分为8类。预报模型采用Green-Ampt入渗模型,下渗系数根据文献[20]确定,土地的曼宁系数根据文献[21]确定,各土地利用类型具体参数见表1。
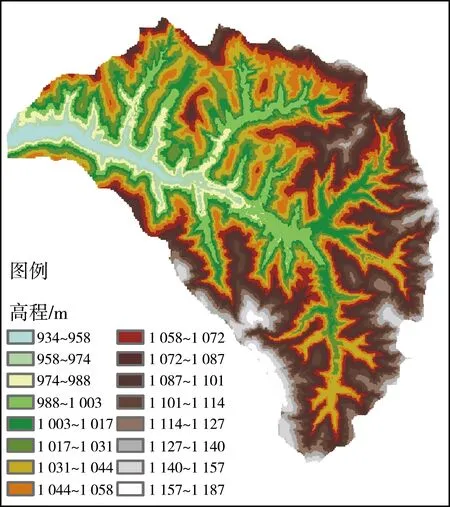
图1 研究区域数字高程
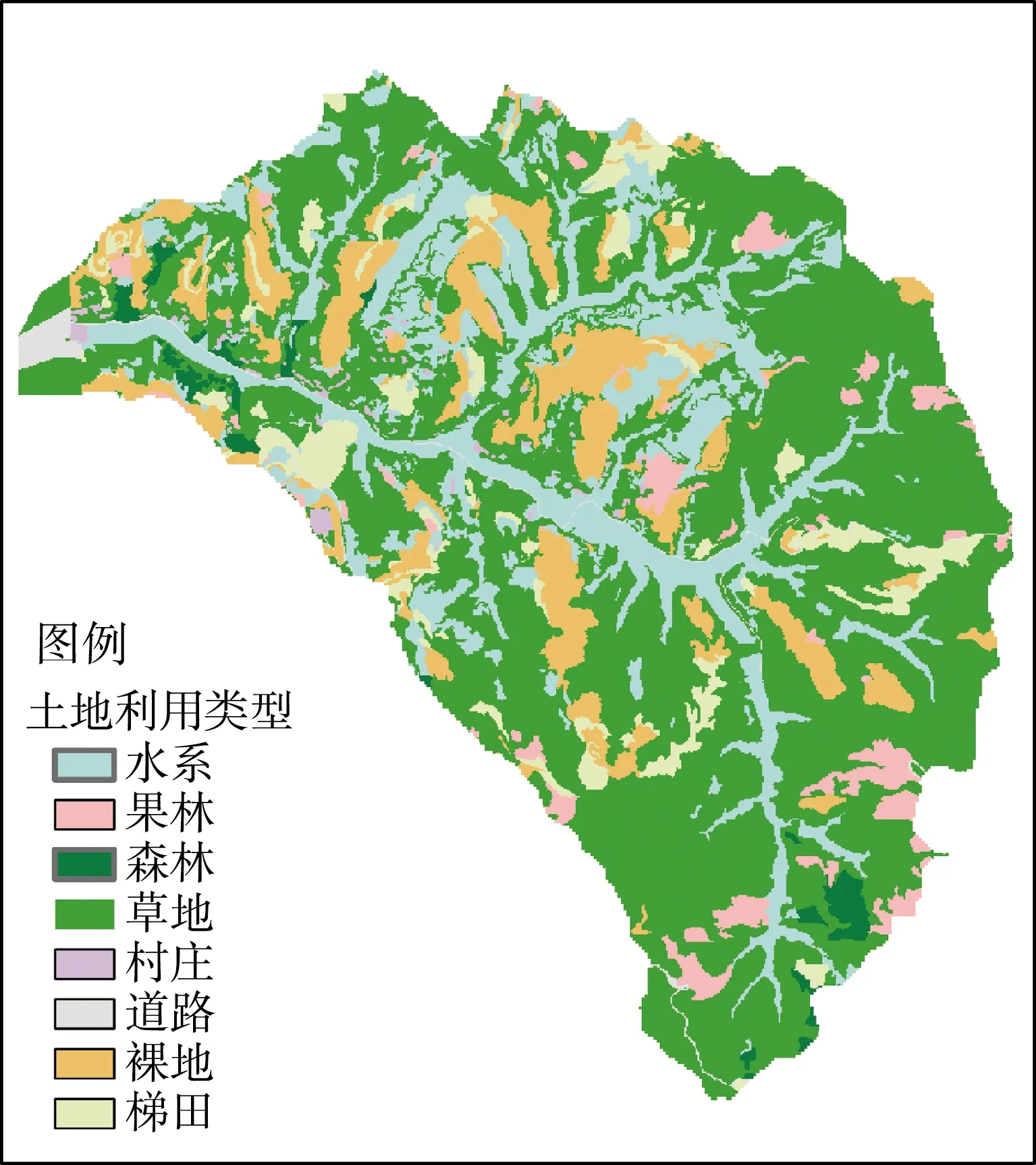
图2 研究区土地利用情况

表1 各类型土地曼宁及下渗参数
1.2 降雨资料
本研究降雨资料时间分辨率取1 h。研究区实测降雨资料有限,仅用历史数据无法完成模型训练,因此,在进行模型训练时,同时加入了历史降雨资料与设计降雨资料。张茹等[22]研究表明GPM(global precipitation measurement)在强降水区域表现出较高的命中率和较低的误报率,卫星产品对强降水的探测能力较优,故历史降雨资料从GPM网站(https://gpm.nasa.gov)获取[23]。本研究主要针对短历时强降雨引发的山洪事件,与芝加哥雨型具有一定相似特征,薛宇雷等[24-25]通过芝加哥雨型生成器生成短历时设计降雨,应用于周河流域及梅溪流域,均取得良好模拟效果。据此,研究选用芝加哥雨型生成器生成各类情况下的短历时设计降雨。榆林市暴雨公式为
(1)
式中:i为暴雨强度,mm/h;p为重现期,a;t为降雨历时,min。
2 快速预报方法
2.1 快速预报流程
为实现山洪灾害快速精准预测,基于水动力模型,结合机器学习算法构建了山洪灾害快速预报模型。预报流程图如图3所示,首先输入地形数据、降雨数据等驱动水动力模型,获得降雨-致洪数据,并将其划分为训练集与测试集,供机器学习算法拟合使用;同时,从降雨数据中提取特征参数,经相关性分析,获取用于算法拟合的最终参数;通过机器学习算法拟合训练集与特征参数,通过网格搜索算法寻找最优参数,获取初步模型;再通过机器学习算法预报结果与水动力模型模拟结果获得误差矩阵,并将误差作为训练数据生成误差修正模型;预报结果由机器学习算法预报模型与误差修正模型共同生成,同时为降低单一算法自身局限性,将两种算法(KNN算法和极限随机树(ERT)算法)结果按其在训练集中评价指标得分进行权值分配,生成混合模型预报结果,并以测试集数据检验模型预报可靠性,若误差过大,将参数调整后重新生成模型,直至预报精度达到要求后,得到最终预报模型。

图3 快速预报流程
洪水淹没范围、过水断面洪峰流量、最大流速以及最大水深是评价洪水风险的重要指标,因地形数据中可能存在的个别噪点会严重影响过水断面的最大深度,因而本文主要采用洪水淹没面积、断面流量、平均流速及水深来评价模型的可靠性。
2.2 水动力模型
模型控制方程为耦合水文过程的二维浅水方程,忽略运动黏性项、科氏力、风应力及紊流黏性项。其对应的二维非线性浅水方程守恒格式的矢量形式表示如下:
(2)
其中
式中:q为变量矢量,包括水深h以及x和y方向的单宽流量qx和qy;u、v分别为x和y方向的流速;F和G分别为x、y方向的通量矢量;r为净雨率;S为源项矢量;zb为河床底面高程;Cf=gn2/h1/3为河床糙率系数;n为曼宁系数。
模型选取对物理问题考虑最全面的动力波法进行地表洪水过程的模拟运算,通过基于Godunov格式的有限体积法进行空间离散求解二维浅水方程[26-27],并运用Runge- Kutta方法构造具有二阶时空精度的MUSCL(monotonic upwind scheme for conservation)型格式,确保物质守恒并有效解决不连续问题[28]。针对模拟过程中可能产生急变流与非连续等复杂问题,模型选用HLLC近似黎曼求解器对单元界面上的质量以及动量的通量进行求解。通过静水重构法处理干湿边界处可能出现负水深的问题[29],并以流速替代单宽流量作为计算变量,可在水深低于或流速高于一定值时,将易失稳的二阶格式有效地转换为稳定的一阶计算格式。保证计算精度的同时,将计算单元中的坡面源项转换为该单元边界上的通量,确保其在进行复杂地形计算时同样满足全稳条件。摩阻源项使用Hou等[30]优化的分裂点隐式法确保运算结果的稳定性。
该模型可对下垫面条件复杂区域进行高精度的雨洪模拟,并采用GPU(graphics processing unit)并行技术加速模拟计算过程,保障模型运算效率。侯精明等[31]对流域模拟数据与实测数据进行了可靠性对比,结果表明模型模拟性能良好;并且随后的文献[32]中另一区域模拟结果与实测数据同样符合,再次验证了模型的可靠性。
2.3 机器学习算法
机器学习是人工智能的核心,包含有SVM、逻辑回归、决策树、随机森林、KNN等算法,本研究主要选用ERT算法及KNN算法构建山洪灾害快速预报模型。
2.3.1ERT算法
ERT算法是Geurts等[33]于2006年提出的一种基于决策树的集成学习算法。该方法类似于随机森林算法[34],通过自上而下的方式生成若干决策树,运用多棵决策树的综合结果进行预测。训练模型时每棵决策树使用相同的训练样本;节点分裂时,省略对GINI系数或均方差的计算过程,采用参数完全随机的方式提升算法的随机性。因节点分裂属性完全随机决定,单棵决策树的拟合精度通常较低,但综合多棵决策树结果,可大幅提升其预报精度。
在ERT算法的众多参数中,模型性能对结点处随机选择的特征个数Max features及构成模型的决策树深度Max depth较敏感。对于同一组训练数据,Max features值越小,模型随机性越强,同时对训练样本的输出值的依赖性越弱。预测误差随Max depth的增加而减小,但Max depth值过大将造成模型的过拟合,致使模型在训练集上可达到近乎完美的表现,但在测试集中会出现较大误差,模型参数的选取需根据具体数据集确定[35]。
2.3.2KNN算法
KNN算法是Cover和Hart基于向量空间模型于1968年提出的一种机器学习算法[36],该算法具有理论成熟、方法简单以及鲁棒性良好的优势,可有效过滤训练集中的噪声。在KNN算法中,每个样本均被视为Rn空间中的向量或坐标点,利用距离公式找出与待分类样本最近的K个样本,以此进行样本估计。其主要步骤如下:
步骤1对已有样本进行实例化,转换为(x,f(x))的形式,其中x为样本的特征参数,x由(x1,x2, …,xn)表示,xn为样本的第n个属性值,即特征参数的数量等于向量组成的维度,实例化后所有的样本构成训练集与测试集。
步骤2给定一个新的测试样本xi,运用距离公式分别计算xi与训练集中各个原本样本之间的距离,并从中筛选出与xi距离最近的K个样本。其距离公式主要有:曼哈顿距离公式、欧式距离公式及闵可夫斯基距离公式等,通过拟合效果综合对比,最终选择在训练集及测试集上均表现良好的欧式距离公式:
(3)
式中:xi、xj为两个样本;xil、xjl分别为xi和xj的第l个特征值;L(xi,xj)为样本xi和xj之间的欧式距离。
步骤3将选择出的K个样本与未知样本的接近程度,按权重分配K个样本的预测结果,并将其分配给新的测试样本,作为预报值。
2.4 基于网格搜索的预报模型参数优化算法
机器学习算法对算法参数十分敏感,算法最大深度、最大特征数等参数的选取不合适将直接导致模型预报的失败。为使预报模型能有效拟合所提供数据,研究采用网格搜索的方法对机器学习算法参数进行优选。网格搜索是一种穷举型算法,可自动模拟各类参数的组合情况,进行多次模型训练,并由交叉验证进行误差对比,最终找到训练误差最小的模型,确定出最适合训练数据的最优的参数组合,进而通过对模型参数的优化提升模型的可靠性。研究中,交叉验证系数选取为0.2,最终确定ERT算法的最大深度为10,误差公式选取均方根误差(RMSE),最小分裂数为2;KNN模型K邻近个数取为3,采用球状树算法进行数据分割,距离公式选择为欧式距离公式。
2.5 误差修正及模型评价指标
为降低由水动力模型及机器学习造成的误差累积,利用水动力模型模拟结果与机器学习算法初步预报结果生成误差矩阵,而后以降雨特征参数为输入条件,误差矩阵为输出结果,运用机器学习算法建立降雨特征参数与误差矩阵之间的对应关系,构建误差修正模型。机器学习算法最终预报结果由初步预报结果累加上误差修正模型所得出的对应误差矩阵生成。同时,为降低由单一机器学习算法本身的缺陷产生的误差,通过将KNN算法模型及ERT算法模型的模拟结果依据其在训练数据集中的确定系数(R2),进行加权分配,获得混合模型预报结果。计算公式为
(4)
式中:RC为混合模型预报结果;RERT和RKNN分别为ERT模型和KNN模型各个网格上的预报结果;SERT和SKNN分别为ERT模型和KNN模型的R2值。
选择R2、绝对平均误差(MAE)和RMSE作为模型整体可靠性的评价指标。
3 结果与分析
在洪水安全应急管理中,决策者最关心的往往是洪水最大淹没面积及洪峰流量情况,据此,通过水动力模型累计模拟108场降雨事件,其中历史降雨事件为18场,设计降雨事件90场,获得其雨洪过程作为样本数据,运用ERT算法及KNN算法训练生成快速预报模型,运用R2、MAE和RMSE评估预报整体性能。此外,在流域主沟道下游出口处选择断面,通过计算出口断面的洪峰流量、流速及由流量与流速近似估算出的断面平均水深对模型预报性能进一步进行复核。
3.1 水动力模型模拟性能验证
快速预报模型的训练数据均为水动力模型模拟结果,因此在进行模型构建时,需先对水动力模型的模拟性能进行验证。模型验证所用降雨资料为王茂沟水文站观测数据,降雨开始于2012年7月15日00:25,降雨历时为5 h,流量资料为王茂沟水文站实测数据,模拟时长为10 h,流域出口处的模拟流量过程与实测流量过程对比见图4。由图4可见,水动力模型模拟结果与观测流量数据变化趋势基本一致,流量峰值滞后约0.5 h,流量消退过程较观测数据稍快,因遥测地形数据与实际地形存在差异,在进行土地利用划分时产生了一定误差,但模型总体效果良好,纳什系数可达0.78,可有效模拟该流域降雨致洪过程。

图4 流域出口流量过程对比
3.2 降雨特征参数相关性分析
在进行机器学习训练时,输入参数的选取至关重要,合理优选参数即可保证模型精度,也可增强模型的时效性[37]。因此,研究选用皮尔逊相关性分析方法对模型所选降雨特征参数进行相关性分析。皮尔逊相关系数小于0.4时为弱相关、极弱相关或无相关,0.4~0.6为中等强度相关,0.6~1为强相关或极强相关。计算公式为
(5)
式中:ρxy为皮尔逊相关系数;σxy是参数x和y的协方差;σx、σy分别为x和y的方差。
选用流域总淹没面积、总淹没水量与所选降雨特征参数进行相关性分析,相关系数计算结果见表2。降雨重现期、降雨峰值、最大3 h降水量、最大5 h降水量、累计降水量及峰值前降水量与淹没面积及淹没水量都具有较强的相关性。总淹没面积、总淹没水量与降雨历时的皮尔逊相关系数分别为0.054和0.096,属于极弱相关或无相关,因此最终降雨特征参数舍弃降雨历时,保留其余参数。

表2 降雨特征参数相关性分析
3.3 预报模型整体性能评估
选取93场降雨事件作为模型训练数据,15场作为测试数据,分别运用ERT算法、KNN算法和混合算法构建山洪快速预报模型,3种模型的统计指标如表3所示。由表3可知,所有模型R2值均可达到0.90以上,说明模型能对数据形成较好拟合,可应用于洪水快速预报研究。在对水深进行模拟时,各预报模型均能获得较好的得分,其中ERT模型略优,R2值为0.958 7,MAE值为0.001 4,RMSE值为0.010 0;在进行流速预报时,KNN模型预报效果最佳,R2值为0.951 7,模拟效果较好,ERT模型预报性能略差于KNN模型。混合模型在对水深及流速的整体预测上表现最好,R2值均达到0.95以上,MAE值和RMSE值均相对较小。
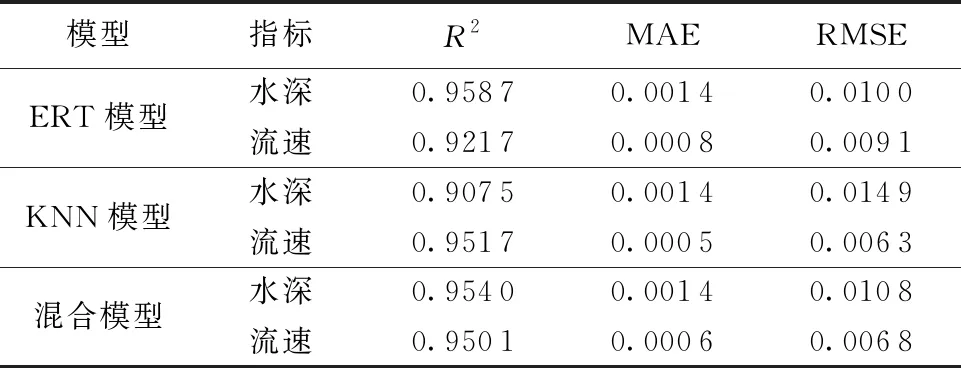
表3 快速预报模型评估指标值
图5为水动力模型、KNN模型、ERT模型以及混合模型在出口断面达洪峰流量时刻的水深图,可以看出,KNN模型、ERT模型以及混合模型在出口断面达洪峰流量时刻,对流域范围内水深模拟结果与水动力模型模拟结果基本一致,能准确反映各处水深与各沟道中的行洪情况。

(a) 水动力模型
图6为水动力模型、KNN模型、ERT模型以及混合模型对15场测试降雨事件模拟淹没面积和淹没水量的结果。图7为KNN模型、ERT模型以及混合模型对淹没面积、淹没水量和平均水深模拟的相对误差,忽略积水深度为10 cm以下的区域,在15场测试降雨事件中,模型对平均水深的预测最准确,对淹没水量的预测效果稍差。由图6可见,KNN模型、ERT模型以及混合模型模拟的淹没面积变化情况与水动力模型模拟结果相同,其中KNN模型误差较为稳定,平均相对误差为0.39%,ERT模型平均相对误差为1.14%,混合模型平均相对误差为0.69%,均达到了近乎完美的拟合效果。淹没面积与淹没水量的平均误差也可控制在5%以内,表明所构建的学习模型能较好反映山洪灾害整体情况,预报性能良好。

(a) 淹没面积

图7 3种模型模拟相对误差
水动力模型需从0时刻开始迭代运算,模拟单场降雨10 h致洪过程平均用时为1 688.4 s,KNN模型对15场降雨数据进行最大洪量预测累计用时为33 s,单场降雨平均用时为2.2 s。ERT模型速度略快,单场降雨平均用时为1.7 s,两类模型均能在极短时间内给出预测结果。混合模型需要综合ERT模型及KNN模型结果,因此模拟用时稍长,单场降雨平均用时约为4.1 s,亦可满足快速山洪快速预报需求。
3.4 流域出口断面分析
因山区地形起伏较大,在将地形网格化进行洪水模拟计算时,地势高的区域降雨将迅速向低洼区域汇集,这会使地势高的区域出现大量积水量极小的网格,因此预报模型在该区域将会达到近乎完美的预报效果,在运用传统指标进行模型可靠性评估时将会过高估计模型的实际预报效果。因此,本文以流域出口断面作为研究断面,通过分析出口断面的流量、流速及平均断面水深进一步验证模型预报性能。在15场降雨事件中,尽管模型在整体指标评估中均得到了较高的分数,但在实际的出口断面处,模型性能仍存在一定差异。4种模型在出口断面处平均水深、平均流速和断面流量模拟结果见表4。
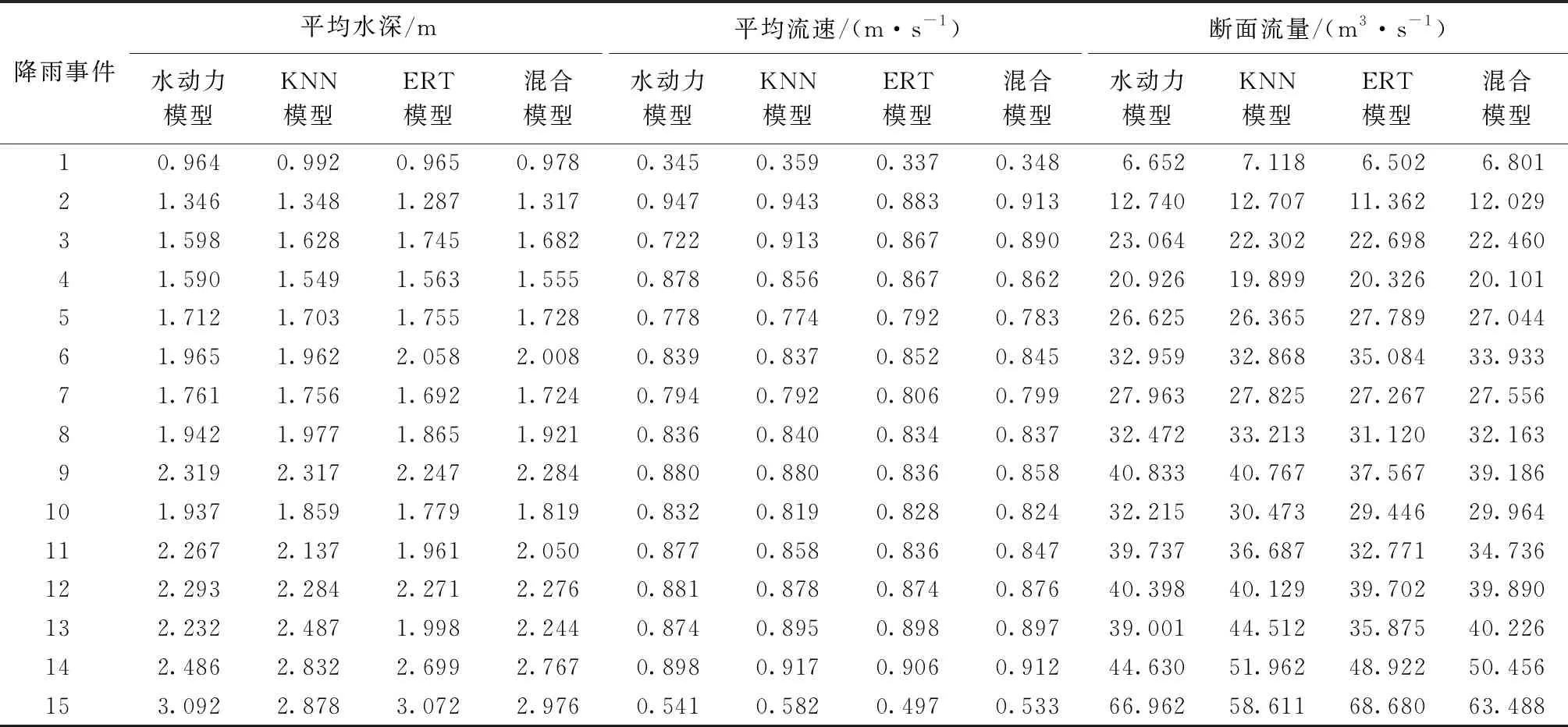
表4 出口断面处平均水深、平均流速和断面流量模拟结果
图8为模型在出口断面的平均水深、平均流速和断面流量的相对误差。由图8(a)可见,3种模型对断面平均水深预测的平均误差均小于10%,其中KNN模型平均误差为3.51%,ERT模型平均误差为5.98%,KNN模型整体误差较小;两种模型在对个别场次降雨模拟时仍然存在较大误差,KNN模型最大误差为13.90%,ERT模型最大误差为13.51%。混合模型平均误差为3.39%,最大单场降雨误差为11.27%,有效综合了两种算法结果,降低对个别场次降雨致洪信息的误报。由图8(b)可见,3种模型在进行流速预测时误差均较小。其中,KNN模型对断面流速预测性能最佳,平均误差为1.85%,比ERT模型低1.03%,同时,最大误差也最小,为6.00%。混合模型平均误差为1.92%,比KNN算法模型预报性能略差,这是由于在对流速进行预测时,KNN模型拟合效果普遍高于ERT模型,在这种情况下混合模型通过综合两种模型模拟结果对误差的校正效果不明显。由图8(c)可见,3个模型对于断面流速及水深的预测准确性要优于断面流量,这是由于断面流量是通过构成断面网格上的水深、流速计算求得,因此存在一定的误差累积现象,导致模型对流量的预报性能稍差。但所建混合模型对断面流量最大误差可控制在15%以内,平均误差为4.50%,低于10%,仍具有较高准确性,可满足紧急决策需求。

(a) 平均水深
4 结 论
a.经评价指标分析,本文选取的机器学习算法在进行山洪灾害预报时均能有较好性能,进行水深模拟预测时,各模型预报均能获得较好的得分,其中ERT模型最佳;进行流速预报时,KNN模型预报效果较好,ERT模型略差于KNN模型,混合模型可有效综合预报结果,可将整体误差控制在5%以内。
b.根据流域出口断面特征信息,算法对断面平均流速预测差距不大,KNN算法表现最佳,平均相对误差为1.85%,混合模型对误差降低不明显;在进行断面水深及流量预测时,算法预报效果差距较大,KNN算法模拟平均水深及断面流量平均误差分别为3.51%和5.10%,ERT算法表现稍差,平均误差均分别为5.98%和6.07%,混合模型对误差校正效果明显,最终平均误差分别为3.39%和4.50%,可为应急决策提供可靠依据。
c.所建模型单场降雨平均模拟时间可控制在10 s以内,可为紧急决策争取大量前置时间,协助决策者更好地采取应急管理措施。

