海堤外坡坡度对波浪溢流量的影响*
黄飞扬,潘 毅,周子骏,姜 昊,陈永平
(1.河海大学 水利水电学院,江苏 南京 210024;2.河海大学 港口、海岸与近海工程学院,江苏 南京 210024;3.南京水利科学研究院,江苏 南京 210029)
波浪溢流[1]是指沿海地区极端高水位和热带气旋产生的风暴潮导致海堤堤前水位超过堤顶、海堤受到越浪与溢流联合作用的现象[2]。在全球气候变暖的背景下,极端气候事件发生的强度和频率都在不断增加[3],这使得发生波浪溢流现象的概率也进一步提高。波浪溢流一旦发生,极易引起大规模的溃堤灾难[4]。2005 年“卡特里娜”飓风风暴潮期间,美国墨西哥湾沿岸由于波浪溢流产生的海堤内坡侵蚀破坏就多达43 处[5],大量的村庄和农田被海水冲毁。自此波浪溢流现象受到了海岸工程界学者的高度重视,波浪溢流也成为了海堤设计和安全评估中必须考虑的因素。
波浪溢流量是指波浪溢流引起的平均单宽越堤流量,是波浪溢流与海堤防护相关的最重要的水力学参数。自2005 年的“卡特里娜” 飓风风暴潮以来,国内外学者对此做了大量研究。2007 年出版的《欧洲越浪手册》[6]最早提出了波浪溢流量的计算方案,此方案作为波浪溢流灾害的应急处理方式直接将波浪溢流量视为稳定溢流量和越浪量的线性叠加;2008 年Reeve 等[7]基于雷诺时均的N-S 方程建立了数值水槽模型来研究不可渗透海堤的波浪溢流量,通过模拟结果拟定出无量纲波浪溢流量表达式;2009 年Hughes 等[8]在几何比尺为25∶1 的梯形截面海堤模型上开展了一系列波浪溢流水槽试验,给出了运用相对出水高度Rc∕Hm0计算波浪溢流量的方法;2012 年Li 等[9]分析大型水槽试验结果,得到了后坡材料为不透水碾压混凝土的波浪溢流量拟合曲线。
虽然Hughes 和Nadal 建立了利用相对出水高度计算波浪溢流量的方法,但是将影响波浪溢流量的原因只归结于溢流与越浪的占比问题;而后Li 等采用了大型水槽模型也得到了不透水海堤平均波浪溢流量曲线,并且在此基础上分析了不同相对出水高度条件下波浪和溢流对波浪溢流量的主导作用。但是上述物理试验都是在外坡坡度为1∶4.25的海堤模型中开展的,忽略了外坡坡度在计算波浪溢流量中的作用。然而van der Meer[10]在越浪的有关研究中指出了海堤外坡坡度对越浪量存在较大影响;波浪溢流作为一种极端的越浪,与越浪过程有很多共同点,海堤外坡坡度对波浪溢流也会存在一定影响,尤其是当水位高于堤顶数值不大时。因此,笔者在现有研究的基础上,采用水槽试验的方式,探讨了海堤外坡坡度对波浪溢流量的影响,提出了考虑海堤外坡坡度的波浪溢流量计算公式。此次研究成果提高了对波浪溢流量的估算精度,能够为波浪溢流期间海堤防御的相关研究和工程措施提供参考依据。
1 波浪溢流模型试验
波浪溢流模型试验在南京水利科学研究院河流海岸所的波浪水槽中进行,在距离造波机53 m处按照1∶10 的试验比尺布置海堤模型,各水力学参数依据弗劳德相似准则进行换算。该物理试验的海堤模型采用了PVC 板制作,中间设置钢架并填充沙石进行固定,接缝处做防水处理以保证模型整体为光滑不透水结构。模型高度为0.325 m、堤顶宽为0.260 m、后坡坡度为1∶3。试验的波浪溢流模拟及流量测量系统包括水槽进出水泵、双向泵、接水箱(包括配套的出水泵)、造波机、水位仪、波高仪、流速仪等。模型布置见图1。
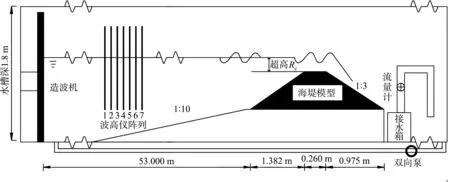
图1 水槽和海堤模型
试验开始时,首先开启水槽进水泵将水槽充水至堤顶,然后开启双向泵产生顺波向水流,此时堤前水位升高、堤后水位迅速降低,从而产生溢流。当溢流稳定后,调节双向泵和水槽进、出水泵控制流量,使得堤前水位达到试验工况所设定的超高,并在堤后形成自由出流。生成稳定的溢流后,开启造波机产生规定波浪要素的波浪(试验采用不规则波,不规则波谱为JONSWAP 谱)。由于本试验的波浪周期较多,为了尽量减少波高仪的移动、提高试验效率,在海堤模型外坡侧安装7 根电容式波高仪(图1),其中数据采集和处理采用DJ800 多点波高仪测量系统,该系统可以实现多个波高传感器的同步测量,误差绝对值小于0.1 mm。整个波高仪测量系统距海堤模型最远距离为6.0 m、最近距离为4.8 m,对不同周期的波浪,至少保证有3 根波高仪满足入、反射分离的间距要求。对于波浪溢流量的测量,由于堤顶水流流速较大且水体较薄,使用流速仪和波高仪测量水流流速和厚度的误差较大,所以本次试验先使用接水箱接取越堤水流,然后再通过流量计抽取箱中水体来间接计算平均波浪溢流量。试验组次见表1,其中海堤外坡坡度为m,有效波高Hm0为不规则波按波高大小次序排列后取前面1∕3 个波的平均波高,谱峰周期Tp定义为JONSWAP 谱中最大谱值所对应的周期,模拟时长T为不规则波到达海堤并且流量变化较为稳定后直至测量结束的试验时长。

表1 试验组次

续表1
2 海堤外坡坡度对波浪溢流影响分析
波浪溢流越堤流量是波浪溢流与海堤相互作用研究中最基本的参数。叠加于海堤稳定溢流上的波浪作用将直接影响越堤水流的形态和大小,在波浪溢流相关研究中主要通过Iribarren 数ξp(即海堤坡度与波浪波陡的比值)判断波浪破碎形式,特别是在堤顶水深较小的情况下,海堤剖面形状结构将会直接改变波浪溢流的越顶方式。本文基于上述物理试验模型,在相同波陡的情况下,通过改变海堤外坡坡度和波浪溢流超高,来观察试验中波浪破碎形式,试验现象见图2。


图2 不同外坡坡度下波浪溢流作用于海堤的过程
由图2 可见,当超高绝对值较小时(|Rc|=0.03 m),稳定溢流叠加波浪后,随着海堤外坡变陡,波浪在堤前破碎程度逐渐扩大,波浪反射程度减弱,并在堤顶前沿发生卷破破碎,产生了大量紊动流体,同时消耗了大量的波能,损耗能量的增加值远大于反射能量的减小值,不规则波列中只有个别大波可以不发生破碎越过堤顶冲向后堤。当超高绝对值较大时(|Rc|=0.06 m),不规则波列中的大部分波浪都能直接越过堤顶,水流状态基本不发生变化,此时海堤外坡坡度对波浪溢流水流特性作用也逐渐弱化。
为了进一步研究影响波浪溢流量的相关因素,对Hughes 和Nadal(2009)与Li 等(2012)的物理模型试验数据进行分析,结果见图3a),其中横坐标为超高和有效波高的比值,定义为相对出水高度,纵坐标为波浪溢流量与波浪相关参数进行组合的无量纲波浪溢流量。可以发现在相同海堤外坡坡度的情况下,无量纲波浪溢流量与相对出水高度在Rc∕Hm0≤-0.3 的范围内具有较好的相关性;而在-0.3<Rc∕Hm0<0 时相关性较差,二者试验数据存在一定的偏差。


图3 本文波浪溢流物理试验数据与前人物理试验数据比较
通过观察图2 的试验现象并分析图3a)的试验数据可知,不同的相对出水高度和海堤外坡坡度都会使波浪溢流的过堤形式发生改变,这种变化在堤顶相对出水高度较大时尤为强烈。利用平均波浪溢流量测量系统,测量不同相对出水高度的波浪溢流,结果见图3b)。其物理试验数据分布与Hughes 和Nadal 公式在趋势上较为吻合。Hughes 和Nadal 公式的表达式为:

式中:qws为波浪溢流量;Hm0为有效波高;Rc为水位超高;g为重力加速度。
在相同外坡坡度条件下,平均波浪溢流量随着相对出水高度的增大而减小。当Rc∕Hm0≤-0.3时,m=2.5 时的试验数据与Hughes 和Nadal 公式计算结果十分接近;而 当-0.3 <Rc∕Hm0<0 时,m=2.5 时的试验数据相较于Hughes 和Nadal 公式计算结果偏大。这主要是由于Hughes 和Nadal 公式中并没有考虑外坡坡度对波浪破碎形式的影响,使得在计算波浪溢流量时存在偏差。为进一步研究海堤结构对波浪溢流量的作用,分析在不同海堤外坡坡度的情况下波浪溢流量的变化情况,建立了如图4 所示的不同波高情况下无量纲化平均波浪溢流量qws∕(gHm03)1∕2随外坡坡度m的变化关系。

图4 不同波高情况下平均波浪溢流量qws∕(gHm03)1∕2随海堤外坡坡度m 的变化
3 考虑外坡坡度的平均波浪溢流量计算公式
由于波浪溢流过程十分复杂,试图从理论上对平均波浪溢流量推导数学公式常常难以得到满意的结果,因此,对于此类问题常采用因次分析方法进行分析。影响波浪溢流量的因素众多,其中相对出水高度是影响波浪溢流量的最主要原因,而当相对出水高度较大时,外坡坡度对波浪溢流量的作用同样不可忽略。
本文在Hughes 和Nadal 公式基础上增加坡度影响参数γm,以反映外坡坡度的影响,使得修正后的计算公式能够考虑到外坡坡度对波浪溢流量的作用。确定平均波浪溢流量计算公式的基本结构形式为:

式中:γm为坡度影响参数;qws为考虑外坡坡度影响的平均波浪溢流量测量值;为Hughes 和Nadal 公式中波浪溢流量的计算值;Rc为超高;Hm0为有效波高,g为重力加速度。图5 给出了不同坡度m分级情况下γm随相对出水高度Rc∕Hm0的变化关系,并选取相同外坡坡度条件下的试验数据进行拟合得到相关曲线。在对数据进行拟合时可以发现不同周期下的波浪溢流量也存在差异。

图5 坡度影响参数γm随相对出水高度(Rc∕Hm0)的变化
由图5 可知,当相对出水高度-0.6<Rc∕Hm0<0时,不同坡度下的有明显的差别,随着相对出水高度Rc∕Hm0的增大,这种差别会更加明显,此时坡度影响参数γm与Rc∕Hm0成指数关系;当相对出水高度Rc∕Hm0≤-0.6 时,波浪溢流主要由溢流占据主导地位,而溢流量只与堤顶水头有关,此时外坡坡度对溢流量几乎没有影响,所以平均波浪溢流量qws与溢流量qs比值随着相对出水高度Rc∕Hm0的减小逐渐接近于1。因此,针对不同坡度影响参数γm,可以使用公式(4)对图5 中的试验数据进行处理:

式中:A、B为经验参数,可根据不同外坡坡度条件下的平均波浪溢流量进行确定;γm为坡度影响参数;qws为考虑外坡坡度影响的平均波浪溢流量测量值;为Hughes 和Nadal(2009)公式中波浪溢流量的计算值;Rc为超高;Hm0为有效波高。
将试验测量的数据代入式(4),分别求解出经验参数A、B的值,计算结果见表2。

表2 不同坡度m 下经验参数A、 B 的值
为了得到不同外坡坡度m下的A、B值,可以通过表2 数据对经验参数A、B进行多项式数据拟合,得到的拟合曲线见图6。

图6 经验参数A、 B 随外坡坡度m 的变化关系
图6 中经验参数A、B的拟合公式为:

采用本文物理试验、Hughes 和Nadal 的物理试验、Li 的物理试验结果对公式(3)~(6)进行验证,验证结果见图7。平均波浪溢流量计算值与各物理试验测量值相关性较好,相较于Hughes 和Nadal 公式加入坡度影响因素的无量纲波浪溢流量公式计算精度更高;Li 的物理试验数据在无量纲波浪溢流量较大条件下与公式计算值相关性较好,而在无量纲波浪溢流量较小的条件下二者相关性较差。由上述分析可知,公式计算值与各物理试验值之间相对偏差都不超过20%。利用本文加入海堤外坡坡度因素影响下的波浪溢流量试验数据对公式(3)的计算误差进行统计,得出公式(3)的决定系数R2为0.993、均方根误差RMSE 为0.344。结果表明公式(3)的计算结果与试验数据吻合,因此公式(3)可以运用到实际波浪溢流量的计算当中。值得注意的是,当无量纲波浪溢流量qws∕(gHm03)1∕2数值小于0.1 时,公式(3)的计算值有所高估,其原因为该范围的数据点超出了试验的研究范围(如图7 中三角形符号所标识的数据范围),因此在超出本试验研究范围的情况下,应谨慎使用本文提出的公式。

图7 平均波浪溢流量计算值与试验值的比较
4 结论
1)相对出水高度Rc∕Hm0的大小影响海堤外坡坡度对波浪溢流量的影响程度。在-0.6<Rc∕Hm0<0的范围内,海堤外坡坡度对波浪溢流量产生明显影响;而在Rc∕Hm0≤-0.6 的范围内,海堤外坡坡度对波浪溢流量影响可以忽略。
2)在-0.6<Rc∕Hm0<0 的范围内,海堤外坡坡度影响到越堤水流形态,进而对波浪溢流量产生影响。海堤外坡坡度从1∶1.5 到1∶4.25 变化的过程中,同等波浪条件下的波浪溢流量呈现先减小后略有增加的趋势。根据试验现象观测,海堤外坡坡度从1∶1.5 变化到1∶2.5 时,波浪溢流量的减小是由于波浪破碎程度的增加消耗了水体爬高的动能;而随着坡度继续变缓,波浪溢流量略有增加则是由坡度变缓引起的波浪爬高增大引起。
3)Hughes 和Nadal 公式未考虑外坡坡度对波浪溢流的作用,但在1∶4.25 的海堤外坡坡度下表现较好,因此本文在Hughes 和Nadal 公式基础上增加坡度影响因子γm以反映外坡坡度的影响,拟合得到了包含海堤外坡坡度m的平均波浪溢流量公式(3),该公式可以计算不同外坡坡度下的平均波浪溢流量,拓展了波浪溢流量的计算范围。应当注意的是,在超出本试验研究范围的情况下,应谨慎使用本文提出的公式。

