密排桩式堤波浪透射系数数值研究*

童朝锋，唐 豪，魏芷阳，孟艳秋，崔国栋

(1.河海大学 港口海岸与近海工程学院，江苏 南京 210098；2.武汉长江航运规划设计院有限公司，湖北 武汉 430030)

密排桩式堤属于透空式堤的一种，与传统防波堤形式相比有诸多优点:可使水流从下部通过，促进内外水体流动，对工程区域自然状况影响较小，适用于深水情况，施工简便，造价低且建筑物对水流影响较小，是一种实用性较强的结构形式。密排桩式堤在波浪作用于桩体上时，反射部分波浪能，又消耗部分波浪能为紊动能，从而达到衰减透射波能的目的，因此密排桩式堤波浪透射率是其设计布置的关键。

防波堤的波浪透射系数，前人主要针对潜堤和浮式防波堤等形式进行研究[1-4]。对于密排桩式堤，Hayashi[5]在1966 年从理论和试验两方面研究单排密排桩式堤的水力特性，经分析发现防波堤中各桩所受的压力和弯矩随桩间距的增大而显著减小，具有很强的经济效应；Hayashi 等[6]还基于小振幅浅水波理论，对防波堤水波理论进行试验研究，修正了关于密排桩式堤波浪的透射和反射理论，考虑水深、堤前半个波长处波高、桩径、桩间净距的影响，得出密排桩式堤波浪透射系数与波浪反射系数计算表达式；Khader 等[7]提出一种由单排八角桩组成的防波堤，并对波浪透射系数和波压力进行分析，将理论分析结果与物模试验结果进行比较，发现与Hayashi 的方法求得的波浪透射系数值吻合良好；Truitt 等[8]通过物理模型试验研究不规则波通过密排桩式堤时的透射系数，发现波高会影响透射系数，但防波堤桩间净距与桩径比值对透射系数影响更大；周明奎等[9]以物理模型试验的方法研究不同桩间距的密排桩式堤在不同波高、周期下的波浪透射系数，结果表明桩间距对波浪透射系数变化有明显影响，透射系数随波高增加而减小，随周期增加变化不明显。

密排桩式堤消浪特征研究大多是基于物理模型试验，随着数值模拟技术的不断发展，不少学者通过数值波浪水槽模拟了波浪与建筑物之间相互作用过程[10-14]，但尚缺少密排桩式堤透射系数的数值研究。本文基于FLUENT 流体力学模型，数值求解Navier-Stokes 控制方程，并采用推板造波法造波和动量源消波法消波，建立数值波浪水槽，设置不同密排桩尺寸和不同波浪要素组合，通过数值模型试验研究建筑物尺寸和波浪要素变化对透射系数的影响。

1 数值模型

1.1 控制方程

利用FLUENT 流体力学模型，在气液两相流体不可压缩假定条件下，数值求解Navier-Stokes控制方程，包括流体质量和动量守恒方程，采用推板造波法造波，采用动量源消波法槽尾消波，建立数值波浪水槽。

流体质量守恒方程为:

式中:t为时间；∇为梯度算子；ρ为流体密度；v为单元流体速度矢量。

动量守恒方程为:

式中:p为压强；ρg为重力项；为应力张量项；μ为动力黏性系数；I为单位张量；∇v为体积变化项；F为流体单元受到的其他源项外力。

采取流体体积函数法(volume of fluid，VOF)跟踪气液两相间自由表面波动，自由液面处以混合流体处理，混合流体密度ρ和动力黏性系数μ由气液密度和动力黏性系数按其体积分数计算得到，混合流体单元气液相流体体积分数满足方程:

式中:αi为自由液面处的流体体积分数，i＝1 为液相，i＝2 为气相，α1＋α2＝1。

通过求解上述流体控制方程及流体单元的体积分数关系，模拟用于透射系数研究的液面波动。

1.2 造波理论

推板造波法的造波原理与实际物理模型中推板式造波机相似。将波浪数值水槽入口边界设置成虚拟推波板，添加动网格，并通过用户自定义功能设置推波板运动速度，使之水平运动带动水体有规律地波动，实现数值波浪的模拟。推板运动速度根据Schäffer[15-16]推得的推板位移变化与波面高度之间解析关系确定，其水平运动速度函数U(t)如下:

式中:η为波面升高；ω为角频率；c0为传递函数；k为波数；d为水深。

二阶Stokes 波波面升高函数表达式:

式中:A为波浪振幅；x为水平方向坐标；t为时间。

1.3 消波方法

在模型后端设置消波区以防止波浪反射影响，消波区采用动量源消波，给消波区水体动量方程添加阻尼源项实现消波效果，动量方程为:

式中:u、w为水平和垂直方向流速；z为垂直方向坐标；ν为涡黏系数；β为消波系数，为使波浪平缓过渡，β值随x坐标值增加由0 递增，其方程表达式为:

式中:a为常数，根据经验其取值范围可取1～50；x0为消波区起始位置水平坐标。

2 试验设置及组次

2.1 数值水槽模型验证

试验验证参考河海大学港池进行的某码头工程密排桩式堤波浪透射试验结果。试验采用透空式密排桩防波堤，防波堤堤顶到地面距离0.25 m，桩长0.128 m，桩径0.33 m，桩间净距0.05 m。试验密排桩式堤结构见图1。

图1 密排桩式堤结构

建立数值水槽验证模型如图2 所示，水槽总长8.5 m、高0.25 m、宽38.4 mm。数值计算中，紊流模型采用k-ε模型(k为湍能，ε为湍能耗散率)，采用耦合速度压力的非迭代算法(pressure-implicit with splitting of operators，PISO)求解控制方程，结合VOF 模型和几何重构法进行液面捕捉，数值水槽中工作区采用非结构化网格，其他区域均采用结构化网格，水槽两端的结构化网格步长取值为:x方向网格步长为25 mm，y方向网格步长为2 mm，z方向网格步长2 mm。水槽中间工作区采用的非结构网格步长为2 mm，时间步长取0.02 s。每步最多迭代40 次，迭代总时间不少于12 s。为确保波浪数值水槽模型试验方法的合理性，数值水槽及其建筑物尺寸与物理试验的尺寸一致，桩帽高度为35 mm。放置于x＝4 m 处，水槽末段设置长1.5 m 的消波区。造波波浪要素采用物理模型试验水深h＝0.163 m时测定的波浪要素对波高以及波浪透射系数进行模型验证，结果见图3。

图2 数值水槽验证模型(单位:m)

图3 模型验证结果

波浪透射系数误差e采用下式计算:

式中:ki为波浪透射系数数值模拟结果；k0为波浪透射系数物理模型试验结果。

通过图3 可看出，模拟的入射有效波高以及堤前、堤后有效波高和计算的波浪透射系数均吻合较好。透射系数模拟值与试验值误差百分比最大为8.95%，最小为2.06%，误差较小，说明所建立的数学模型模拟结果较为准确，可用于密排桩式堤波浪透射模型试验的模拟研究。

2.2 数值试验模型设置

用于试验计算的波浪数值水槽建立方法和过程与验证模型采用方法一致。模拟高13 m、长450 m 的数值波浪水槽，水深为10.8 m，消波区长60 m。密排桩的结构布置与网格划分与图2 一致，其中桩长为7.7 m，桩帽高度为2.3 m，数值水槽工作区非结构化网格步长为0.1 m，其他区域均为结构化网格，x方向网格步长为1.5 m，y和z向网格步长为0.1 m。

根据文献[9]的研究可知，影响堤波浪透射系数大小的因素主要有波陡、密排桩桩径、桩间距等，因此设置模拟工况如下:所有工况下的波周期为7.0 s，水深10.8 m，波长61.39 m。桩径从小到大分别取1、3、5 m，桩间净距从小到大分别取0.2、3.2、5.2 m，不同尺寸的建筑物分别对应0.015、0.030、0.045 这3 种波陡，用以探究桩径、桩间净距、波陡对密排桩式堤波浪透射系数影响。

3 结果与分析

3.1 桩径对透射系数的影响

采用数值模型试验模拟得出的不同波陡和桩间净距条件下，波浪透射系数与桩径的相关关系如图4 所示。桩间净距和波陡相同时，波浪透射系数随桩径增大先快速后缓慢地减小，建筑物对波浪阻挡作用随桩径增大逐渐增强。

图4 不同波陡条件下波浪透射系数与桩径关系

3.2 桩间净距对透射系数的影响

不同波陡和桩间净距条件下，波浪透射系数与桩间净距的相关关系如图5 所示。波陡和桩径相同时，桩间净距越大波浪透射系数越大，密排桩式堤消浪效果越差。且在桩间净距小于2.2 m时，波浪透射系数随桩间净距增加速度较快，桩径净距大于2.2 m 时增加速度较慢。这是由于建筑物其他尺寸不变，桩间净距较大时，建筑物对波浪阻挡作用较弱，随着桩间净距无限增大，建筑物对波浪的抵御效果趋近于0，波浪透射系数的增速也就越缓慢，此时波浪透射系数会逐渐趋近于1。

图5 不同波陡条件下波浪透射系数与桩间净距关系

3.3 透空率对波浪透射系数的影响

建筑物透空率η′的计算公式为:

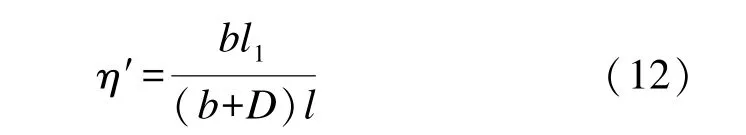
式中:l1为密排桩式防波堤桩长；l为密排桩式防波堤总高程。

不同波陡对应的波浪透射系数随透空率变化如图6 所示。可以看出，波浪透射系数随透空率增加而增加，且随透空率增加波浪透射系数值增速越来越低，透空率η′＜0.3 时增加速度较快，η′＞0.3增加速度较慢，此规律与文献[9]的物理模型试验结果相符。

图6 波浪透射系数随透空率变化

3.4 相对干舷高度对波浪透射系数的影响

不同建筑物相对干舷高度下波浪透射系数变化见图7，通过比较相同波陡条件下，建筑物相对干舷高度的变化所对应的波浪透射系数值变化，判断相对干舷高度对波浪透射系数的影响情况。从图中的波浪透射系数变化可看出，在干舷淹没情况下，密排桩整体位于水面下，随着淹没程度的增加，波浪的透射系数逐渐增加，密排桩对波浪的抵御效果逐渐减弱，当淹没至一定高度时，密排桩对波浪的影响效果较小，此时波浪透射系数也基本保持不变；非淹没状态下，水位位于建筑物下方，随着水深的减少，干舷距离水面高差逐渐变大，水面下降初期由于波浪受到桩帽的影响，波浪透射系数有所增加，随着干舷距离水面高差的进一步增大，波浪在密排桩的掩护下透射系数基本维持不变。

图7 不同相对干舷高度下波浪透射系数变化

3.5 波陡对波浪透射系数的影响

桩径分别为1、3、5 m，桩间净距b分别为0.2、2.2、4.2 m 时波浪透射系数随波陡变化如图8 所示。可以看出，随着波陡变化，波浪透射系数并没有明显变化规律，与文献[9]的关于桩式防波堤波浪透射系数随波陡增加而减小的研究结果不符。分析认为是由于本文研究的密排桩式堤结构桩顶部为桩帽，而文献[9]研究的桩式结构为等间距排列的圆桩，没有上部结构。当本文建筑物透空率较小时其结构形式接近于直立式潜堤，波浪透射系数随波陡增加而减小，当建筑物透空率较大时其结构形式接近于透空式防波堤，此时波陡对波浪透射系数没有明显影响。

图8 波浪透射系数随波陡变化

3.6 透射系数计算公式拟定

结合试验考虑的各因素对波浪透射系数的影响，根据试验结果可看出，影响波浪透射系数的因子主要有波陡(Hs∕L)、建筑物透空率(η′)、建筑物相对干舷高度(Rc∕Hs)，因此可建立密排桩式堤波浪透射系数(kt)无量纲函数表达式:

基于模型试验结果，采用多元函数非线性回归拟合的方法，拟合建立了带桩帽的密排桩式堤波浪透射系数与各影响因素的相关关系式:

拟合公式计算值与实测值对比如图9 所示，公式计算与数模试验值拟合后，两者相关系数为0.81，均方根误差为0.25，同时将公式与物理模型试验数据进行对比验证，两者相关系数为0.82，均方根误差为0.23。因此可在适用范围内利用公式对带桩帽的密排桩式堤透射系数进行估算。

图9 透射系数公式计算值与实测值对比

4 结论

1)密排桩式堤波浪透射系数随桩径增加先快速后缓慢减小；随桩间净距和透空率增加先快速后缓慢增大；干舷淹没情况下，透射系数随淹没程度的增大而增大并趋于平稳，非淹没状态下，透射系数随干舷距离水面高差的增大先增后趋稳；波陡对波浪透射系数没有显著影响。

2)基于数值模拟试验结果数据，拟合建立了密排桩式堤波浪透射系数随入射波波陡、建筑物透空率、建筑物相对干舷高度变化的计算表达公式(14)。