基于Apriori算法的特殊路段事故致因关联规则挖掘研究

文｜陈彬 于鹏程 张奇

【导读】

道路交通事故严重威胁人民群众的生命财产安全，影响经济社会的和谐稳定。为深入排查事故隐患，防范消除安全风险，进一步推进道路交通事故预防“减量控大”工作，本文通过Apriori算法对隧道、桥梁和弯坡路三种特殊交通环境下的交通事故致因进行关联规则挖掘，用以发现事故致因间的关联关系，可对道路交通事故防控起到一定的指导作用。

事故致因；关联规则；Apriori算法

一、藕合分析方法

为实现事故致因间的藕合分析，本文采用了挖掘关联规则的方法，其本质就是挖掘要素间的频繁项集合。以形式化的描述方式，介绍关联规则如下：

设I={I1,I2,I3,...,Ii,...,In}是一个项集总集，其中Ii表示第i个项，n为项的总数。事务ti表示I的某个子集，而由若干个事务t组成的集合D={t1,t2,t3,...,tn}为事务数据库。

在衡量项集间的关系时，常采用两个度量值：支持度（support）和可信度（confidence）。

支持度是指某个待分析项集占据数据总项集的比例关系。公式如下：

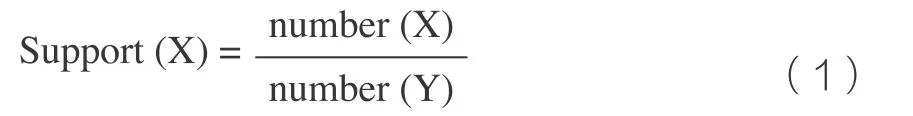
其中，Support(X)表示X项目的支持度，number(X)表示X项集的频数，number(N)表示数据集总项集的频数。而“最小支持度”则是根据经验预设定的一个阈值。

可信度也叫做置信度，是指两个具有关联的项集之间的比例关系。表示为前项项集出现的情况下，后项项集出现的概率。公式如下：

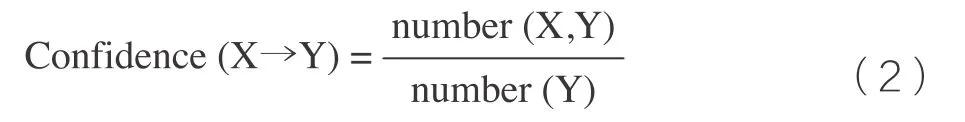
公式（2）的计算可以看作求条件概率Confidence(X|Y)，表示Y事件发生的条件下，X发生的概率，分子number(X,Y)表示X和Y两个项集都出现的频数。同理，“最小可信度”也是根据经验预设定的一个阈值。而在实际计算可信度时，往往直接根据已有的支持度数值做除法获得，公式如下：

推荐理由:本书专门研究和论述战略思维。战略思维能力，就是高瞻远瞩、统揽全局，善于把握事物发展总体趋势和方向的能力。马克思主义为我们正确认识和妥善处理中国特色社会主义事业中诸多重大关系，树立全局眼光、提高统筹能力提供了思想武器。

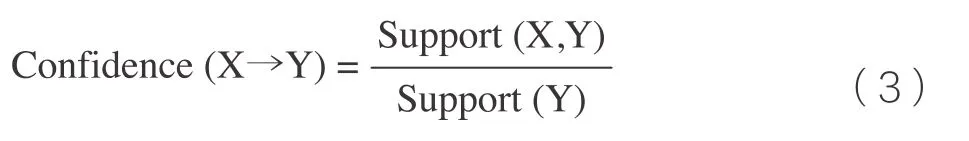
在最小支持度和最小可信度的选取上，一般有两种方式：根据经验和常用阈值数值进行规定设置，或者针对具体问题具体分析，直接选取前百分之N作为结果。

频繁项集挖掘，就是在已达到预设最小支持度的项集中，计算可信度。可信度也达到预设阈值后，才满足强关联规则的条件。本文根据频繁项集自身的性质，推导出两个原则，在寻找频繁项集时以此作为剪枝条件，可以简化计算复杂度，提高寻找频繁项集的效率。原则一是频繁项集的所有非空子集也为频繁项集；原则二是若某一项集不是频繁项集，则包含该项集的所有项集都不是频繁项集。

二、使用算法简介

本文实验主要选取经典的关联规则挖掘算法，即Apriori算法。该算法的原理如下：

第一步，输入数据集，从单元素开始计算支持度，筛选出满足最小支持度的频繁一项集；第二步，从这些频繁一项集中连接各个元素生成两个元素的候选二项集，计算支持度，筛选出频繁二项集；第三步，以此类推，直到不能生成新的频繁项集为止；第四步，从频繁二项集开始计算可信度，筛选出满足最小可信度阈值的关联关系；第五步，以此类推，遍历所有的频繁项集，进行第四步操作；第六步，至此，所有满足最小支持度和最小可信度阈值的关联关系，即为强关联规则。

以10条模拟事故数据分析为例，简单介绍Apriori算法的整体过程：事故数据如表1所示。10条记录共包含5种因素：夜间行驶、大雾天气、路面结冰、酒后驾驶、山路隧道。预设支持度阈值为0.2，可信度阈值为0.7。

表1 模拟事故数据

首先，遍历10条事故数据，通过计算事故因素的频数，计算出每个致因的支持度，生成候选一项集C1，再将支持度与阈值0.2做对比，将大于等于阈值条件的项作为频繁一项集L1（因为C1各项都满足，所以这里L1等于C1），如表2所示。

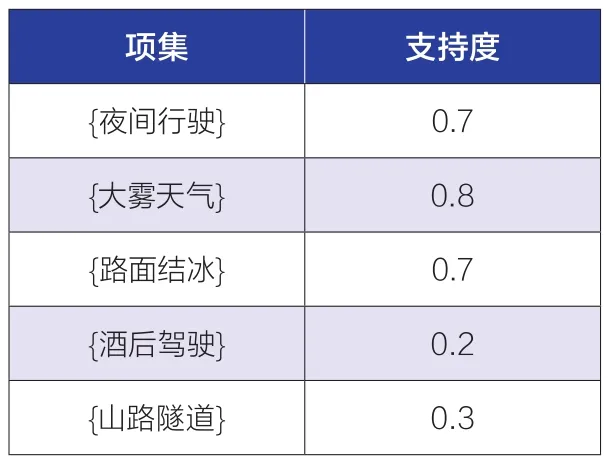
表2 候选一项集C1（频繁一项集L1）

通过L1中的频繁项，再遍历10条数据，生成候选二项集C2，以此类推，最终得到候选三项集C3和频繁三项集L3（这里计算得出恰好C3等于L3），结果如表3所示。

表3 候选三项集C3（频繁三项集L3）

L3中的两个集合自然连接的结果为{夜间行驶，大雾天气，路面结冰，山路隧道}，根据频繁项集的性质1可知，如果该自然连接结果也是频繁项集，那么其所有非空子集都应该也是频繁项集，但很明显其3项子集只有L3中的2个是频繁项集，所以不满足性质1，已经不能再衍生出频繁项集L4。至此，得到了所有的频繁项集和其支持度数值。

下一步，从L2开始，计算每个频繁项集中各个元素间的可信度。{夜间行驶，大雾天气}的可信度计算如下：

因为Confidence(夜间行驶→大雾天气)=0.71＞0.7，所以由“夜间行驶”推测出“大雾天气”是强关联规则。

表4所示为该10条记录的所有强关联关系计算结果。

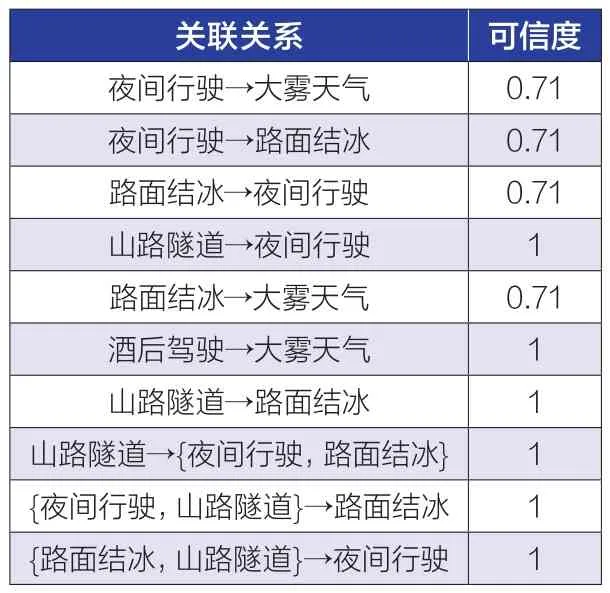
表4 关联关系结果

三、实验分析

（一） 实验数据和关联属性

实验分析使用道路交通事故抽样数据，抽样范围为2015年至2019年间的道路交通事故，记录了“数据编号”“事故发生时间”等在内的33项属性，以及“人员编号”“人员类型”等21项附加属性。经数据处理后，发现有16项事故影响属性可能与事故发生存在强关联关系，如表5所示。

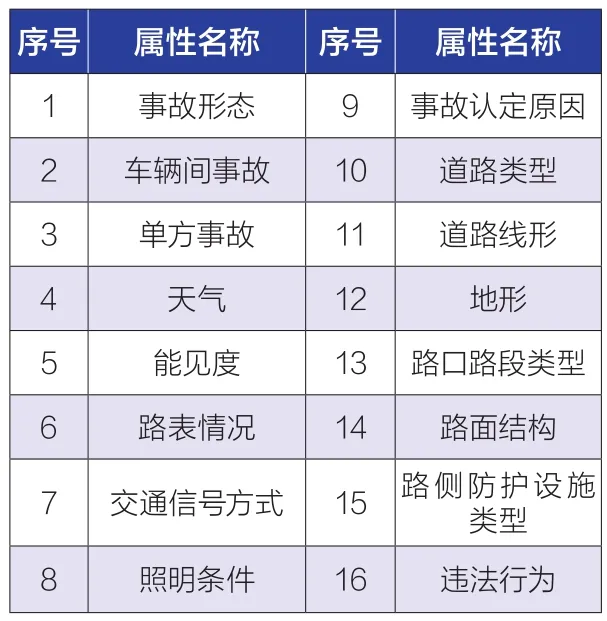
表5 事故记录属性

（二）实验条件和实验结果

本文实验针对三种特殊路段场景进行关联分析，包括隧道、桥梁和弯坡路。为了保证实验结果不遗漏有效信息，实验设置上相对选取了较小的最小支持度（min_Sup）阈值和最小可信度（min_Conf）阈值。

1.隧道场景

隧道场景下，取最小支持度min_Sup = 10/N（隧道），其中N（隧道）为隧道场景下数据采样量总量。取最小可信度min_Conf= 0.05。通过python编程，经Apriori算法计算，典型违法行为和事故形态间的强关联规则示例，如表6所示。

表6 隧道场景强关联规则结果

2.桥梁场景

桥梁场景下，取最小支持度min_Sup = 10/N（桥梁）、最小可信度min_Conf = 0.05。通过python编程，经Apriori算法计算，典型违法行为和事故形态间的强关联规则示例，如表7所示。

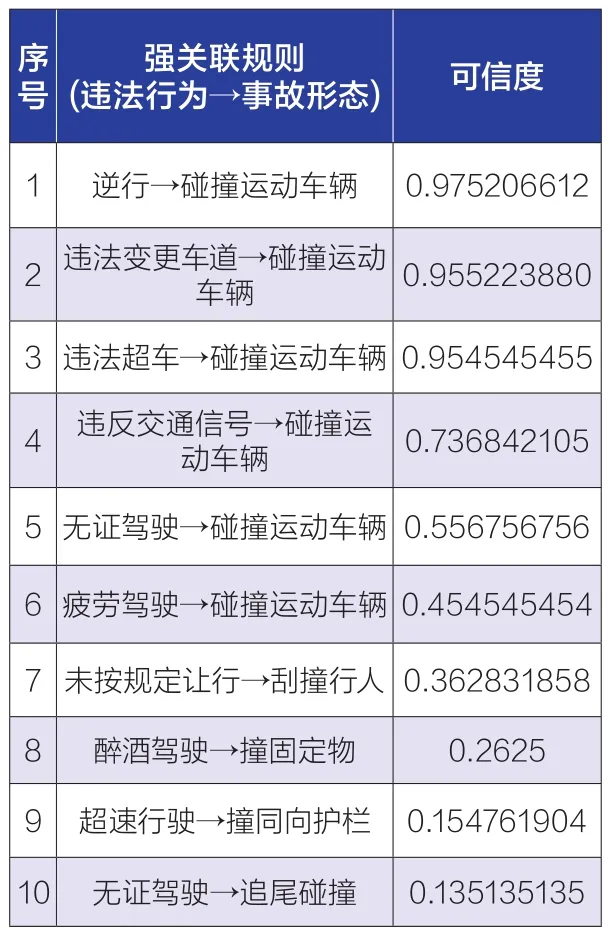
表7 桥梁场景强关联规则结果

3.弯坡路场景

弯坡路场景下，取最小支持度min_Sup=100/N（弯坡路）、最小可信度min_Conf=0.05。通过python编程，经Apriori算法计算，典型违法行为和事故形态间的强关联规则示例，如表8所示。

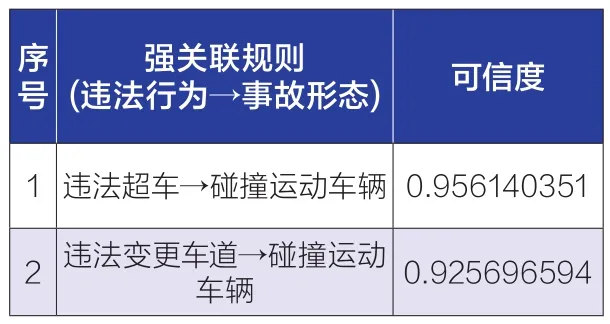
表8 弯坡路场景强关联规则结果

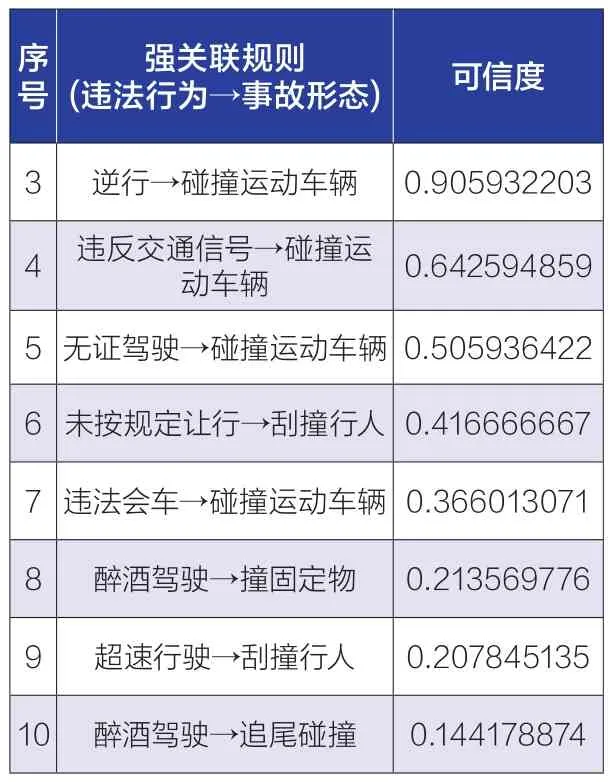
序号强关联规则(违法行为→事故形态) 可信度3 逆行→碰撞运动车辆 0.905932203 4 违反交通信号→碰撞运动车辆 0.642594859 5无证驾驶→碰撞运动车辆 0.505936422 6 未按规定让行→刮撞行人 0.416666667 7 违法会车→碰撞运动车辆 0.366013071 8 醉酒驾驶→撞固定物 0.213569776 9 超速行驶→刮撞行人 0.207845135 10 醉酒驾驶→追尾碰撞 0.144178874

（三）实验分析和总结

根据三组实验的数据结果，隧道、桥梁和弯坡路场景下的强关联规则既有相同性，也有差异性。

相同性主要体现在：一是在发生事故的前提下，发生“碰撞运动车辆”的事故形态的强度都很高。最高在隧道场景下，“违法超车”“违法变更车道”的行为发生时，会有100%的概率导致“碰撞运动车辆”的事故结果；最低在隧道场景下，“醉酒驾驶”的行为会有约48%的概率导致“碰撞运动车辆”的事故结果。二是三种特殊路段场景下，强关联规则相似。“违法超车”“逆行”和“违法变更车道”三种违法行为的强关联规则强度都很高，在90%以上。

差异性主要体现在：一是不同场景下相同违法行为导致相同事故形态的关联度有差异。“逆行→碰撞运动车辆”的关联，在三种场景的关联度都在90%以上，但是“疲劳驾驶→碰撞运动车辆”在隧道场景下的关联度在61%左右，而在桥梁场景下的关联度在45%左右，在弯坡路场景下的关联度在36%左右。“无证驾驶→碰撞运动车辆”“违反交通信号→碰撞运动车辆”的关联，在三种场景的关联度也存在一定差异。二是不同场景下相同违法行为导致不同事故形态的关联度上有差异。“醉酒驾驶”违法行为，在隧道场景下导致“碰撞运动车辆”的事故形态在48%左右；在桥梁场景下导致“撞固定物”的事故形态在26%左右；在弯坡路场景下导致“追尾碰撞”的事故形态在14%左右。

四、规则完善

使用Apriori算法对事故数据进行关联规则挖掘分析，可以精准定位到各因素间的关联关系，指导道路交通事故防控。下一步计划从两个角度进行优化研究：一是将关联规则分析由单点分析拓展为多维度分析；二是进行多种事故场景分类综合对比分析，最终形成事故致因的关联规则库，为道路交通事故预防“减量控大”工作提供支撑。