非整数极距次级双边直线感应电机推力特性计算

刘慧娟,张 千,宋腾飞,张振洋

(北京交通大学 电气工程学院，北京 100044)

长初级双边直线感应电机(Double-sided Linear Induction Motor，DLIM)的次级质量轻、结构简单、可靠性高，适用于航母舰载机电磁发射、无人机弹射、碰撞试验系统等短距离大加速度的应用领域[1-2].

针对大推力电磁弹射用长初级双边直线感应电机，文献[3-4]提出了多定子共用同一次级的电机结构，并分析了定子之间的耦合作用.文献[5]分析的十二相长初级双边直线感应电机，相较于多定子电机，降低了电机的损耗，提高了效率，并解决了弹射系统中电力电子器件容量和系统冗余等关键问题.文献[6]提出的发卡式全填充绕组及开槽次级结构提升了长初级DLIM的功率密度，减小了推力波动.文献[7]对比了栅格次级和平板次级电机的性能，得出采用栅格次级能有效规范横向气隙磁场，提高电机的力功比[7].求解直线感应电机电磁性能、对电机性能优化设计主要采用有限元法(Finite Element Method，FEM)和解析计算两种方法[8-9].其中等效电路是解析计算的主要方法[3,5,10]，能直观反映电机的阻抗参数[11].对长初级直线感应电机的研究，次级长通常为整数极距，且以初级作为运动参考坐标系建立其矢量磁位方程[12-15]，求解等效电路参数并计算其性能.采用初级作为运动参考系虽能有效地反映电机的稳态推力性能，由于没有考虑边界条件随次级运动的产生变化，导致解析计算求解的推力波动频率主要为两倍电源频率，与实际为两倍滑差频率不符[16-17]，且计算电机推力忽略了后退行波磁场的影响[16].文献[18]通过解析计算说明了后退行波磁场在调速范围内对气隙磁场以及推力特性的影响.

与短初级直线电机结构不同，长初级双边直线感应电机的次级为长度有限的金属板，因此其长度可为非整数极距的任意值.然而，次级的长度对电机推力性能的影响，鲜有学者关注.长初级双边直线感应电机的次级长为非整数极距时，正常行波磁场产生的电磁推力还包含一定幅值的推力波动.因此，为考虑次级的长度对长初级双边直线感应电机稳态推力以及推力波动的影响，以长初级DLIM的次级为运动参考系建立求解模型，基于文献[18]，本文作者首先推导了恒流源供电时非整数极距次级DLIM的气隙磁场、次级电密的实数域表达式，并分析气隙行波磁场和次级电密的分布特点.其次，求解了气隙磁场分量和次级电密分量两两相互作用产生的电磁推力以及其波动的表达式.计算了各电磁推力分量的特性曲线，定量分析了由端部效应产生的推力对合成电磁推力的作用.最后，通过有限元电机模型计算的结果验证解析方法求解的电磁推力表达式的正确性.

1 气隙磁密

1.1 气隙磁通密度表达式

非整数极距次级DLIM截面如图1所示，图1中，L1为每段初级长度，L2为次级长度.根据假设条件[16]建立的以次级板为运动坐标系的电机数学模型如图2所示，模型由初、次级耦合区Ⅰ，无次级的非耦合区Ⅱ和Ⅲ组成.

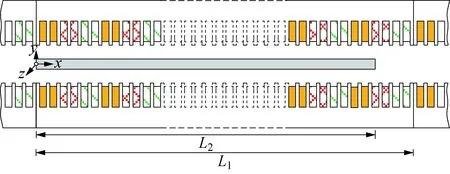
图1 非整数极距次级DLIM横截面示意图Fig.1 Cross section of long primary DLIM with secondary of non-integral pole pitch length

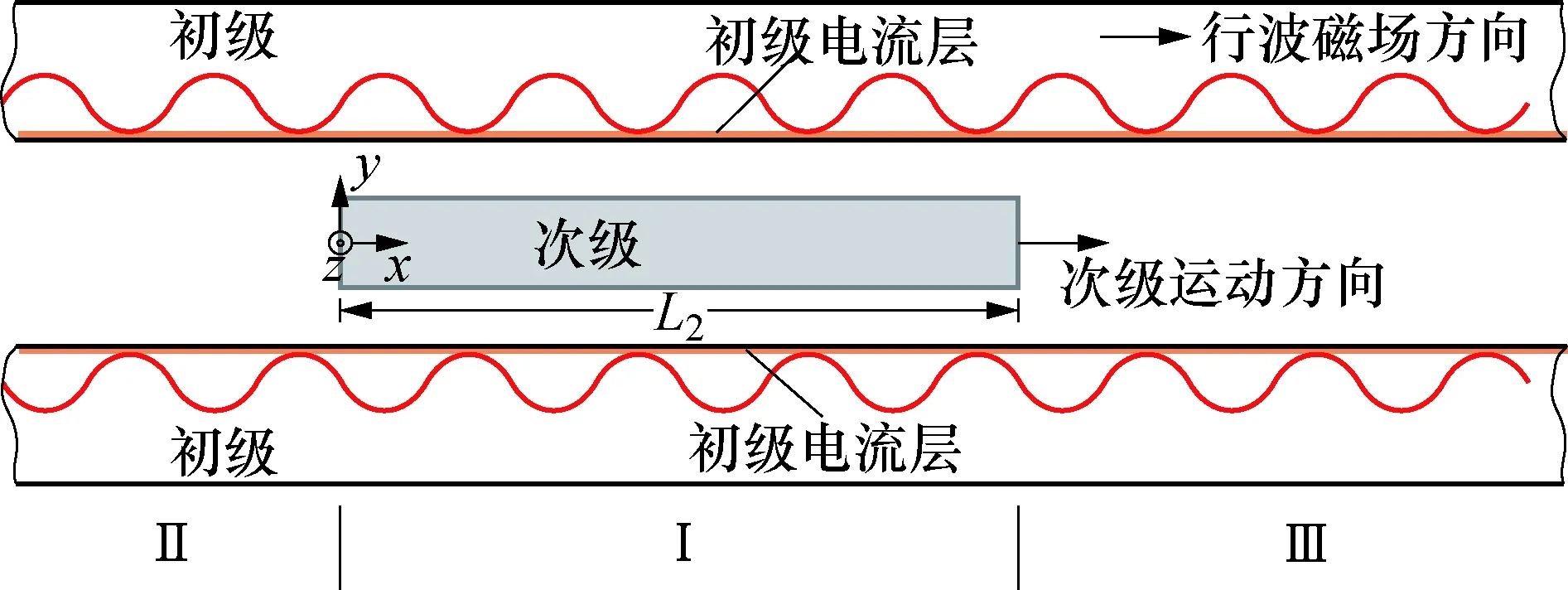
图2 非整数极距次级电机数学模型Fig.2 Mathematical model of DLIM with secondary of non-integral pole pitch length

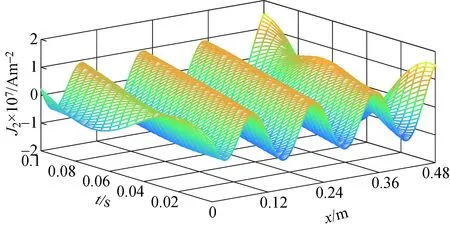
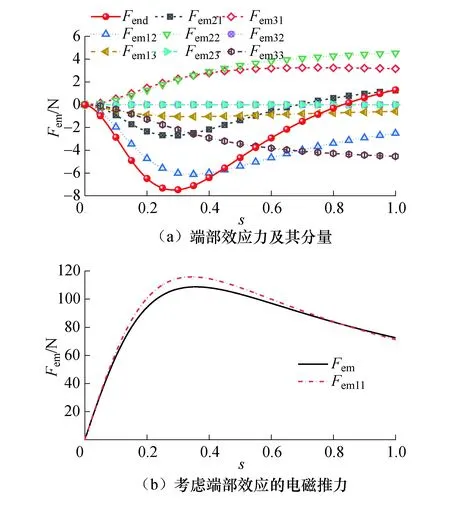
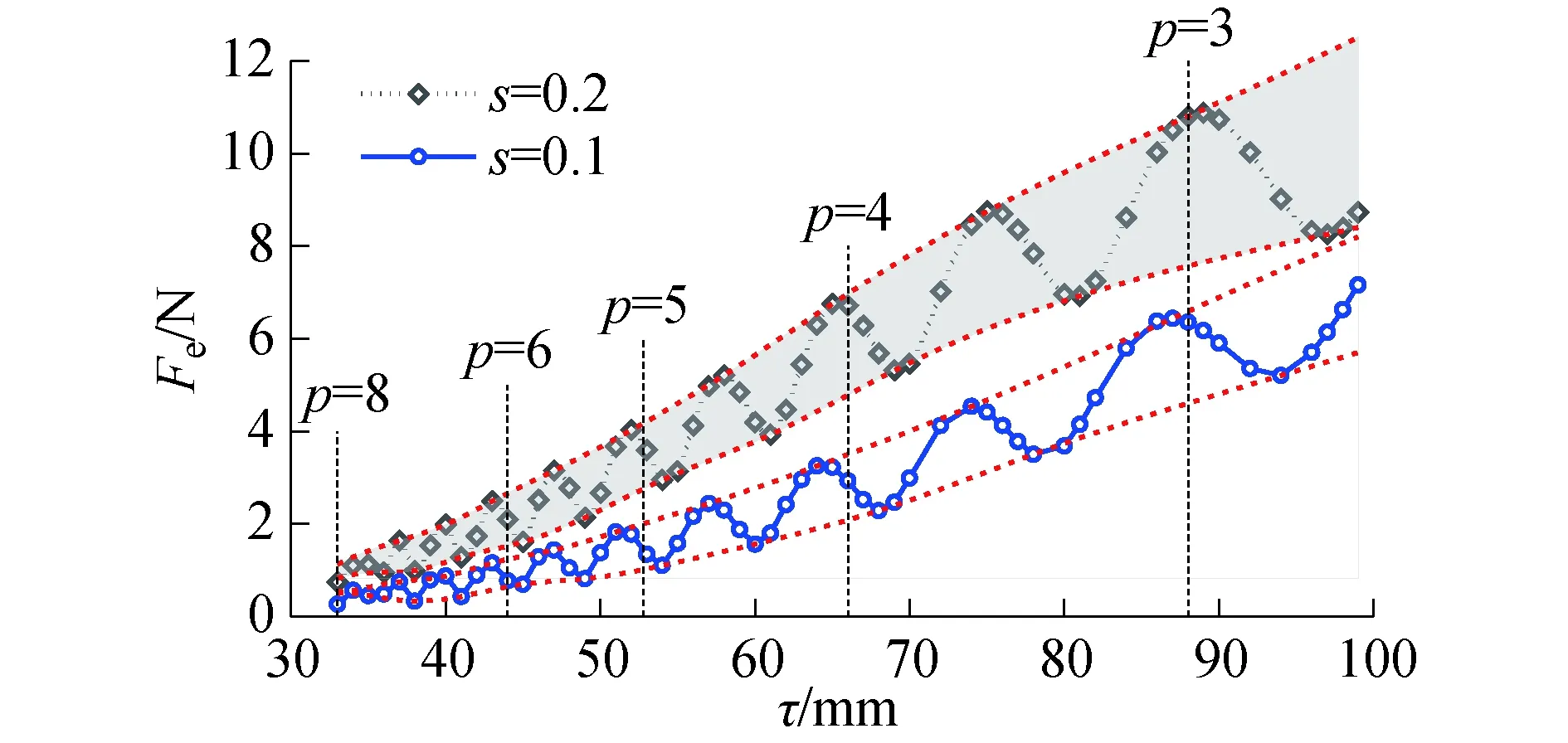
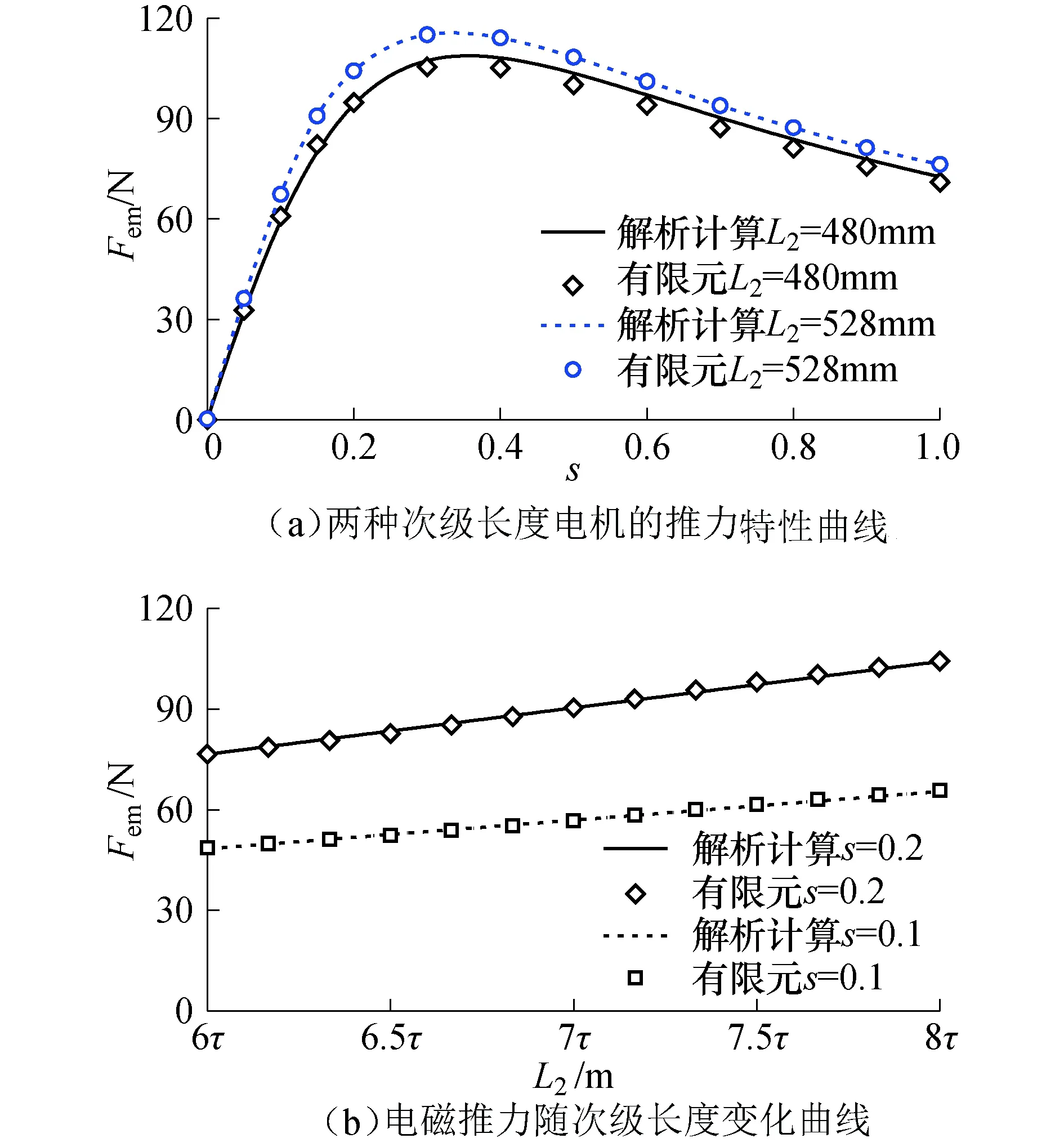
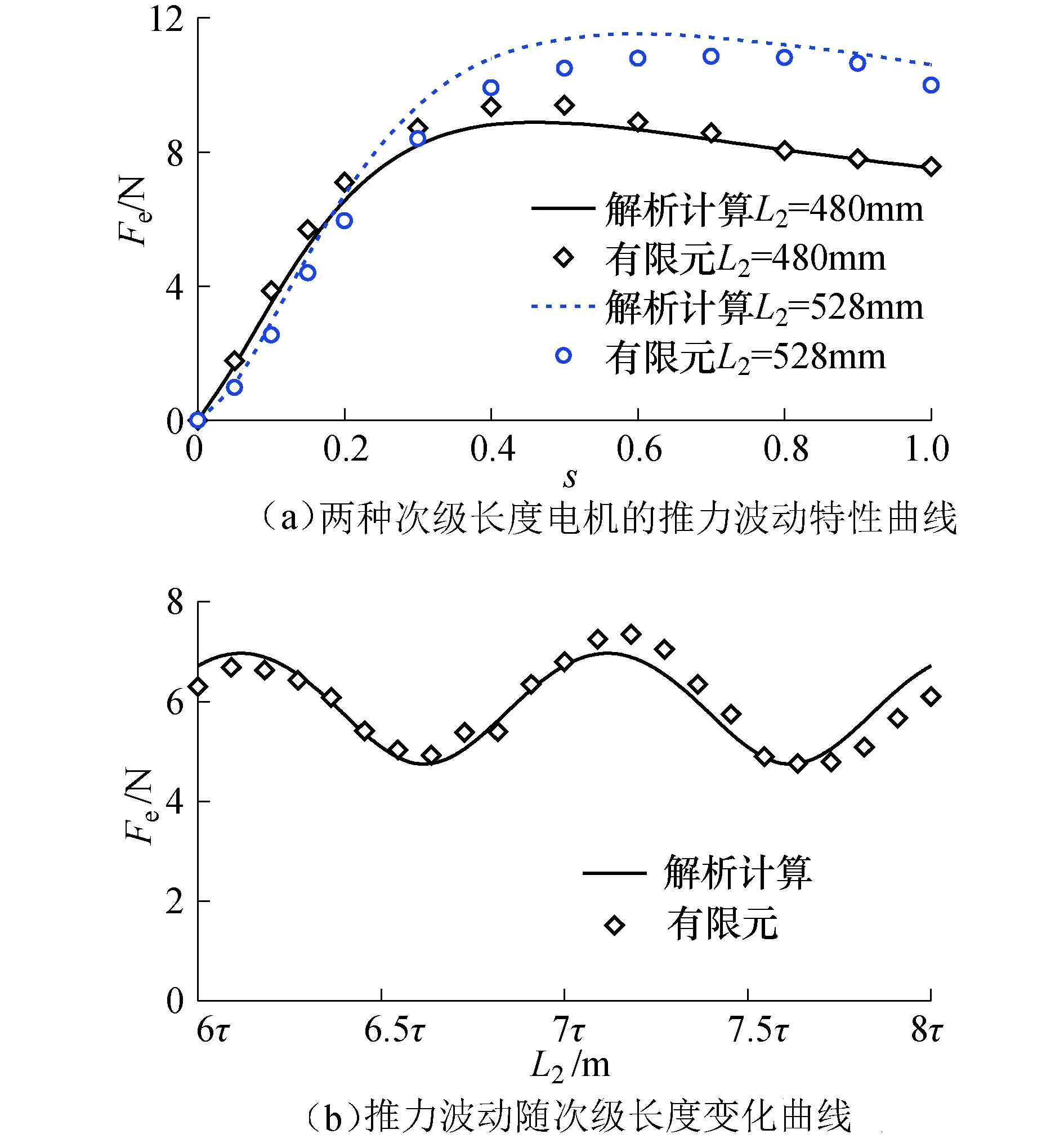
根据麦克斯韦方程组[21]，建立气隙磁场微分方程，并带入相应边界条件，求得耦合区域0

(1)

(2)

式中：s为滑差率；ω为电源角频率；μ0为真空磁导率；δ为等效电磁气隙长度；m1为相数；τ为极距；σs为次级导体面电导率；J1为初级电流层密度；G为电机的品质因数.

非整数极距次级DLIM耦合区I中的气隙磁场与整数极距次级电机的磁场相似[18]，其中B1y1为正常行波磁场，B1y2为前进行波磁场，B1y3为后退行波磁场.不同的是，整数极距次级长为2pτ，极对数p为整数，后退磁场B1y3相位中kL2=2pπ，因而可忽略不计.

非耦合区域Ⅱ、Ⅲ中气隙磁场与次级长无关，其实数域表达式为

(3)

1.2 气隙磁场分布

以表1中电机参数为例，分析非整数极距次级电机的气隙磁场分布特征以及力特性.

表1 长初级双边直线感应电机参数

耦合区Ⅰ以及次级两端非耦合区Ⅱ、Ⅲ的气隙磁通密度分布如图3所示，端部效应导致耦合区域气隙磁场在纵向存在畸变，气隙磁场的端部效应分量集中在次级两端一对极距范围内.

图3 气隙磁场分布Fig.3 Distribution of air gap flux density

不同滑差率时,合成气隙磁场幅值包络线如图4所示，图中0≤x≤0.48 m为初、次级耦合区域.耦合区内磁通密度幅值随滑差增大而减小，由于非耦合区域存在激励，次级两端的磁通密度幅值接近空载气隙磁通密度幅值.x<0 m以及x>0.48 m的非耦合区内气隙磁通密度幅值与滑差大小无关.

由于气隙磁通密度中仅B1y3的相位与次级长度相关，因此次级长仅影响合成气隙磁场出端相位，而不影响其幅值.与文献[18]对比分析表明，非整数极距次级DLIM与常规整数极距次级DLIM在耦合区内的气隙磁通密度的分布规律一致.

图4 合成气隙磁通密度包络线Fig.4 Envelopes of air gap flux density

2 次级电密

2.1 次级电密表达式

根据建立的磁场微分方程求得次级电密实数域表达式为

(4)

次级电密由正常分量j21、前进分量j22和后退分量j23组成.前进电密分量和后退电密分量的衰减时间常数均为1/α.

2.2 次级电密分布

根据式(4)可得次级电密的时间、空间分布如图5所示.次级电密为时间的正弦函数，空间上由于存在端部效应，在次级的出端和入端一对极距范围内存在较显著的畸变.

图5 次级电密分布Fig.5 Secondary current density distribution

滑差变化时次级电密幅值沿次级运动方向(纵向)分布如图6(a)所示，滑差s=0时，次级与初级磁场无相对运动，次级板中电密为0 A/m2.滑差率较小时，次级电密的后退分量增加出端电密幅值，前进分量减小了入端电密幅值，由于衰减时间常数1/α较大，前进和后退电密分量衰减较慢.滑差较大时，端部效应同时增大出端和入端电密幅值，此时衰减时间常数1/α较小，次级电密较快衰减至正常电密分量幅值；电机堵动，即s=1时，次级电密最大幅值在次级出端，其值超过正常分量的幅值两倍以上.

滑差率为0.2时，不同长度次级的电密纵向分布见图6(b).由于次级电密的正常分量幅值为恒定值，前进、后退分量幅值在次级两端一对极距范围内均能衰减至较小值，而衰减时间常数1/α与次级长度无关，因此，不同长度次级电机的电密分布趋势是一致的.

图6 次级电密纵向分布Fig.6 Longitudinal distribution of secondary current density

3 电磁推力

非整数极距次级的双边直线感应电机的电磁推力为

(5)

式中：2a为初级铁心宽度.推力表达式中除了含有恒定的推力Fem外，还含有不产生时间平均推力波动分量Fe.

3.1 稳态电磁推力表达式

求解式(5)可得，考虑纵向端部效应前进行波磁场和后退行波磁场所产生的总稳态电磁推力可表示为

(6)

其中，基本行波磁场与正常电密、前进电密、后退电密分量产生的电磁推力Fem11、Fem12、Fem13分别为

(7)

f11为正常行波推力密度，正常行波推力Fem11与次级板的长度成正比.

前进行波磁场与正常电密、前进电密、后退电密分量产生的电磁推力Fem21、Fem22、Fem23分别为

(8)

后退行波磁场与正常电密、前进电密、后退电密分量产生的电磁推力Fem31、Fem32、Fem33分别为

(9)

式中

(10)

推力分量Fem12、Fem13、Fem21、Fem31中包含衰减系数e-α的项的数值接近0N，可忽略不计.所有推力分量均可由正常行波推力密度表示.

除正常行波推力Fem11外，各推力分量之和为端部效应力Fend.

Fend=Fem12+Fem13+Fem21+Fem22+

Fem23+Fem31+Fem32+Fem33

(11)

滑差率s≠0时，端部效应力不为0，表明纵向端部效应影响电机的输出推力.

3.2 稳态推力特性分布

由式(7)～(11)可得，次级长度为0.48 m时，端部效应力及各分量、正常行波电磁推力Fem11以及输出电磁推力Fem等电磁力特性曲线如图7所示.

正常行波磁场与次级电密的前进、后退分量产生的电磁力Fem12、Fem13与正常行波推力Fem11方向相反，为减弱正常行波推力的制动力.由衰减方向相反的气隙磁场和次级电密分量积分得到的电磁力分量Fem23、Fem32的数值远小于其他电磁力分量，约等于0N，对合力贡献可忽略不计.Fem21的方向与k-α有关，α

因此，电机的稳态电磁推力求解可简化为

Fem=Fem11+Fem12+Fem13+Fem21+Fem31

(12)

端部效应力Fend可简化为

Fend=Fem12+Fem13+Fem21+Fem31

(13)

随滑差增大，端部效应力Fend，先增大后减小，主要表现为阻碍次级运动的制动力.

图7 电磁力特性曲线Fig.7 Characteristic curves of electromagnetic force components

保持磁动势幅值和次级长度不变，极距变化时，可知次级长度不恒为整数极距.不同极距电机的推力特性曲线如图8所示.

图8 不同极距电机的推力特性曲线Fig.8 Thrust characteristic curves of motors with different pole pitch

由于初级电流层密度与极距成反比[17-18]，系数k与极距成反比，等效电磁气隙随极距增大有较小幅度减小，由式(7)可知，对推力起主导作用的正常行波推力最大值与极距成反比，正常行波推力与滑差以及极距的关系为

(14)

因此推力特性随极距变大而变软，最大电磁推力随着极距增大而减小.

3.3 推力波动表达式

求解式(5)可得，推力波动Fe包含的9种分量为

(15)

基本行波磁场与正常、前进、后退电密分量产生的推力波动Fe11、Fe12、Fe13分别为

(16)

前进行波磁场与正常、前进、后退电密分量产生的推力波动Fe21、Fe12、Fe23分别为

(17)

后退行波磁场与正常、前进、后退电密分量产生的推力波动Fe31、Fe12、Fe23分别为

(18)

气隙磁场分量与次级电密分量两两相互作用产生的推力波动分量可使用正常行波推力密度f11表示，推力波动频率均为两倍滑差频率，与短初级双边直线感应电机推力波动频率为两倍频不同[17].

3.4 推力波动

根据式(16)～(18)绘制的推力波动的瞬时波形如图9所示.当次级长度为非整数极距时，正常行波磁场与次级电密正常分量作用产生的正常行波推力波动Fe11不为0，即正常行波磁场也产生一定幅值推力波动，而当次级长度为整数极距时，该项值为0N.波动分量中Fe23和Fe32分别由衰减方向相反的前进行波磁场与电密后退分量、后退行波磁场与电密前进分量相互作用产生，二者的波动幅值近似为0N，对总推力波动基本无影响.

正常和后退行波磁场产生的推力波动Fe11+Fe12+Fe13、Fe31+Fe33构成了总推力波动Fe主要部分，前进行波磁场产生的波动幅值较小.各推力波动分量中，由正常行波磁场与电密后退分量产生波动Fe13以及后退行波磁场与电密正常分量产生波动Fe31幅值较大，是推力波动主要来源.

图9 推力波动的瞬时波形Fig.9 Transient waveform of thrust ripple

保持磁动势幅值和次级长度不变，极距变化时，推力波动随极距增大呈现发散上升趋势，如图10所示.次级长度不变时，减小极距，极数相应增多，可减小推力波动.减小极距虽然能降低推力波动，但过小的极距会给电机制造带来困难，因此极距的选择需要综合考虑各方面约束条件.

图10 不同极距电机的推力波动Fig.10 Thrust ripple of motors varies with pole pitch

4 推力特性比较验证

通过FEM瞬态场仿真模型计算了非整数极距次级双边直线感应电机的电磁推力和推力波动特性曲线，以验证解析表达式的准确性.

4.1 计算电磁推力比较

次级长度分别为整数极距528 mm和非整数极距480 mm时，通过解析表达式计算的推力特性曲线与有限元计算的结果如图11(a)所示，解析法与有限元法计算结果吻合.有限元仿真计算的推力证实了推导的电磁推力解析表达式的正确性.

滑差率分别为0.1和0.2时，两种方法计算的电磁推力随次级长度变化如图11(b).由于次级长度通常大于2对极，端部效应力幅值与次级长度无关，端部效应力基本不受次级长度影响，且正常行波推力正比于次级长度，因此推力随次级长度线性增加.

图11 推力有限元验证Fig.11 Verification of analytical thrust by FEM

4.2 计算推力波动比较

次级长度分别528 mm和480 mm时的推力波动特性曲线如图12所示.

图12 电磁推力波动验证Fig.12 Verification of thrust ripple by FEM

两种次级长度电机的推力波动滑差特性曲线的趋势与推力特性曲线一致，在电机稳定工作区，推力波动随滑差增大而增大.

电源频率和滑差率一定时，推力波动值是次级长度的正弦函数，其周期为一个极距.次级长度为非整数极距，若长度取值合适，正常行波推力波动可抵消一部分端部效应推力波动，从而获得比次级长为整数极距时更小的推力波动值.

由于在解析计算过程中做了一定合理的假设，因而解析法计算的电磁推力、推力波动与仿真结果之间存在一定的误差.

5 结论

1)气隙磁通密度的时空分布规律与次级长度无关；端部效应的存在增加次级出端电密幅值，减小入端电密幅值.

2)次级长度为非整数极距时，端部效应电磁力在电机稳定工作区表现为阻碍次级前进的制动力.正常行波磁场和后退行波磁场是推力波动的重要来源.

3)次级长度不为整数极距时，正常行波磁场和电密正常分量产生一定幅值的波动分量.极距一定时，合适的次级长度可有效减小电机的推力波动.次级长一定时，合适的极距也可有效减小推力波动.