自适应学习率的增量强化学习飞行控制

刘俊辉，单家元，荣吉利，郑 雄

(1.北京理工大学宇航学院,北京 100081；2.北京理工大学飞行器动力学与控制教育部重点实验室，北京100081；3.中国运载火箭技术研究院，北京100076)

0 引 言

近年来，导弹、火箭等飞行器自主学习飞行控制问题得到广泛关注，未来复杂任务迫切需要增强弹/箭复杂飞行环境适应能力及突发事件的应对能力。跨域强对抗环境作战，未知环境与非预定任务场景下侦察、打击或对抗，由于飞行场景和任务变化，大气密度、飞行速度、环境温度、障碍物发生很大改变以及飞行器本体动力学发生突变等，传统的针对预先已知使用场景和作战任务而进行增益调度设计的飞行控制器需要各特征点下精确的系统模型，在未知、未探明环境中很难获得，并且设计过程非常繁琐，亟需突破以智能控制为核心的自主学习飞行控制技术，以弥补程序化控制策略带来的局限性，提升飞行器在复杂未知环境与突发事件下的自主性、强适应性与鲁棒飞行控制能力。

强化学习控制方法是一种不依赖于对象动力学模型并对环境变化与模型时变特性具有较强鲁棒性的控制方法，为飞行器自主飞行控制提供了有效可行的思路。强化学习方法起源于计算机领域，几乎同一时期最优控制领域学者Werbos, Bertsekas等开展了类似的近似动态规划和神经元动态规划的研究。这些方法的理论根基是1956年Bellman提出的动态规划方法。为了解决动态规划方法的维度灾难及逆向求解问题，Werbos在1977年提出了近似/自适应动态规划方法，该方法融合了强化学习和动态规划的思想。后续，强化学习方法在计算机和控制领域分别迅速发展，并且在航空航天领域进行了广泛探索研究，包括直升机、运载器、变体飞行器、制导系统的自适应飞行控制。为了实现在线求解飞行控制律，通常采用时序差分法(TD)来求解强化学习问题。TD结合了动态规划法和蒙特卡洛法(MC)的优势，既不需要对象与环境的模型，也不用端到端的训练过程，可以实现飞行控制器实时迭代更新。

自适应Actor critic designs(ACD)是一种基于TD的方法，结合Actor-Critic结构、动态规划、和神经网络的自适应/近似动态规划方法，是设计自适应最优飞行控制器的有效方法。ACD将策略评价(critic)和策略更新(actor)分离设计，能适应未知环境得到最优控制策略。ACD方法可以分为：启发式动态规划(HDP)、双启发式动态规划(DHP)、全局双启发式动态规划(GDHP)。DHP与HDP方法的区别在于DHP评价网络用于近似值函数相对于状态的偏导，而HDP的评价网络用于近似值函数。GDHP方法是结合DHP与HDP的一种强化学习方法。但是这些方法都需要在线或离线辨识被控对象的精确模型。直接在线辨识对象的精确模型耗时较长，很难在线完成，而事先的离线辨识又由于环境或模型不确定性无法获得对象的精确模型。文献[11-12]通过输入-输出数据辨识被控对象增量模型，提出了基于增量模型的双启发式动态规划方法(IDHP)，很好地解决了模型精度与在线实时计算的矛盾，并应用于飞行控制器设计。相比于直接辨识被控对象模型的DHP方法，IDHP具有更快的在线学习速度和更高的控制精度。

IDHP自主学习飞行控制律分为控制律学习阶段和飞行控制运行阶段。在控制律学习阶段，IDHP基于一定的学习策略，通过施加持续激励，采集系统响应数据来迭代更新行动和评价权值网络的权值，实现控制器的学习。但是并不是所有的控制器参数都能通过学习获得，在实施神经网络权值系数迭代学习之前需要根据一定的经验和收敛性分析确定动作和评价神经网络权值、学习率等超参数。不同的学习率对系统稳定性和控制精度有较大影响。文献[13]提出了两阶段切换控制策略，在预先训练阶段采用PID控制器辅助，并基于粗精度-高精度训练不断迭代训练神经网络权值系数，运行阶段采用IDHP控制器，此方法减轻了训练阶段控制的振荡，提高了学习成功率。但是，现有的方法大多是事先设定学习率、神经网络初值等超参数，而事先设定超参数的方式无法适应飞行器速度、大气密度大幅变化以及变体飞行器气动特性等被控对象动力学特性大范围变化情况下的自主飞行控制。文献[4]结合监督学习与强化学习，提出了监督Actor-Critic控制结构，监督结构提供额外的信息来进行评价反馈以“成形”最优学习策略，加速收敛。Dias等提出一种针对飞行器容错控制的基于监督器触发在线自适应学习控制。受文献[4,14]启发，本文提出一种自适应调整学习率的增量强化学习飞行控制方法，以适应飞行器动力学特性大范围变化时的自主学习飞行控制。

本文的主要贡献在于设计了一种基于梯度下降法的在线调整强化学习动作网络学习率超参数的算法。具体为：

1)在强化学习评价网络、动作网络和模型网络三层结构的基础上增加性能监督器，提出了基于实时控制性能监督评估的学习率在线调整框架；

2)利用小波分析方法构造飞行控制器稳定度实时量化评估指标，在线评估不同学习率参数下控制系统稳定度，为学习率参数实时调整提供依据；

3)将学习率在线调整转化为非线性优化问题，基于梯度下降法实现了学习率参数在线优化，提高了增量强化学习飞行控制律的成功率及在飞行器动力学特性大范围变化下的适应性，减轻了IRL飞行控制算法对预先设定学习率参数的依赖。

1 增量强化学习飞行控制律设计

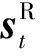
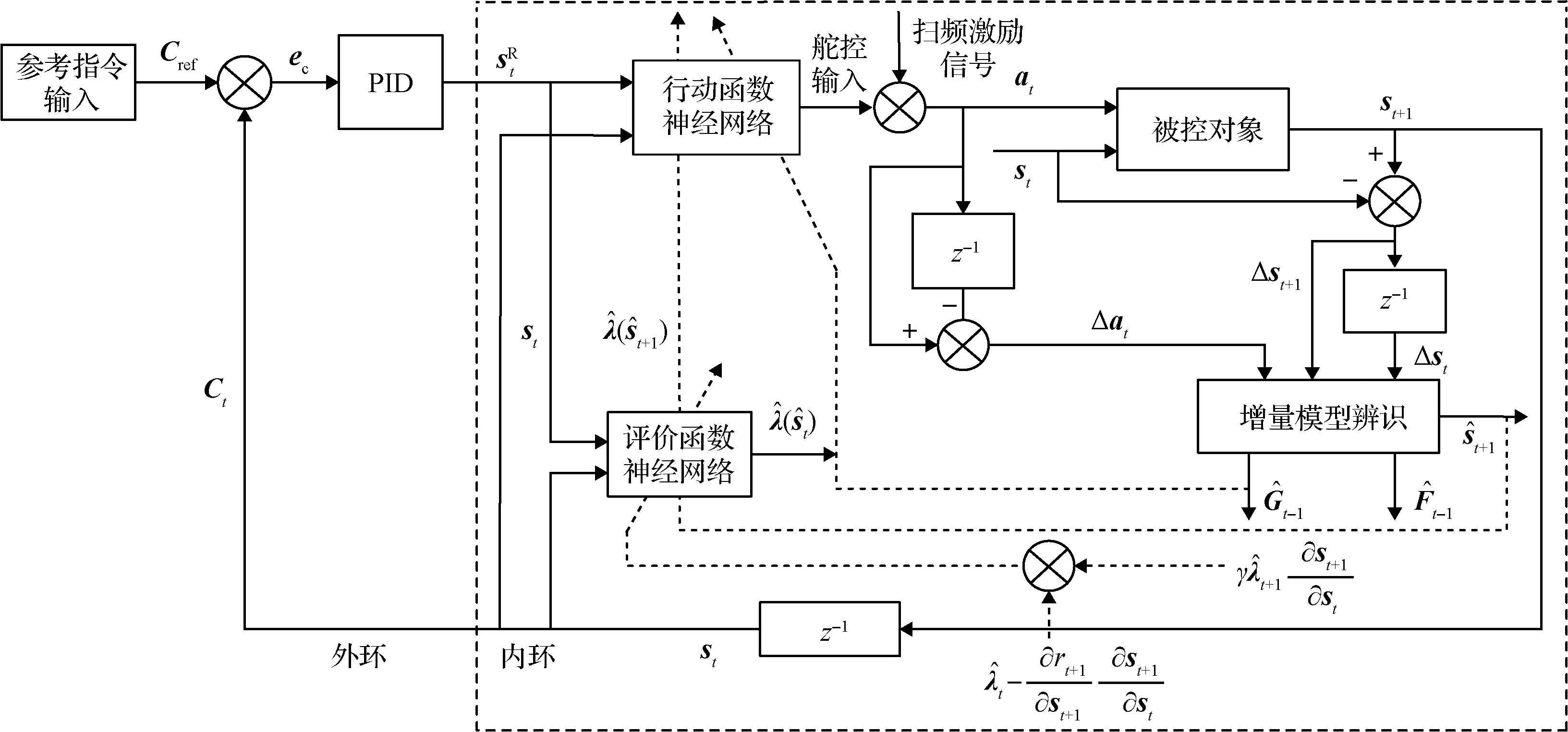
图1 增量强化学习简略图(实线表示前向信号流，虚线代表自适应调整路径)

1.1 问题描述

利用强化学习来求解飞行控制问题，首先要明确状态转移关系和价值函数。在高频采样假设条件下，基于离散时间模型描述非线性系统状态转移函数(,)∈×1，如式(1)所示。其中∈×1表示状态向量，∈×1为动作向量，和分别为状态向量和动作向量维数。

+1=(,)

(1)

式中：下标表示当前时刻，下标+1表示下一时刻。

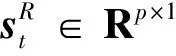
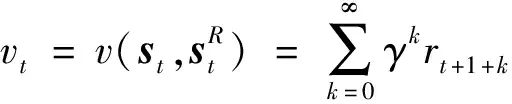
(2)

控制的目标是使飞行状态跟踪参考指令信息，因此一步回报函数设计为下一步状态与参考状态偏差的二次型形式

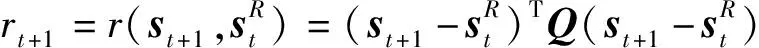
(3)

式中：∈×为给定的正定矩阵，下一步状态+1需要基于在线辨识模型进行预测。的取值将影响强化学习控制律的收敛性，较大的能够加快学习算法的收敛速度，而过大的容易使学习算法发散。

最优化控制策略为使价值函数取最大值的控制策略，如下式所示

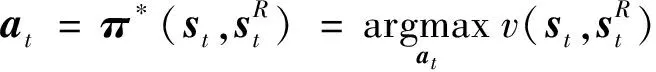
(4)

1.2 强化学习飞行控制问题求解

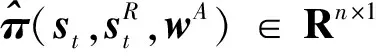
基于最小化TD误差原理来更新评价网络权值系数。评价网络更新的目标是使误差函数(5)最小。

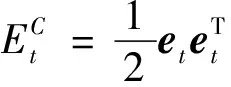
(5)

其中,误差定义为价值函数相对于状态量偏导的时序差分误差。

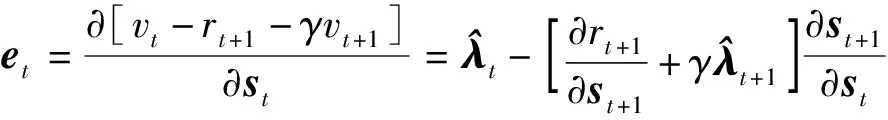
(6)

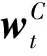
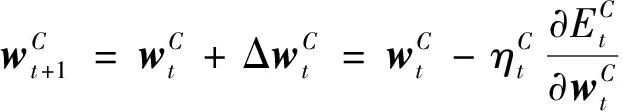
(7)

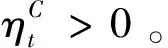
误差函数相对于权值系数的梯度计算公式为

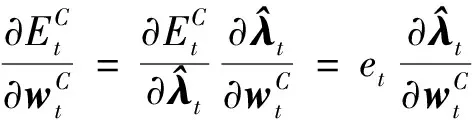
(8)

动作网络更新的目标是最大化值函数，基于Bellman最优性定理可以得到：

(9)

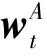
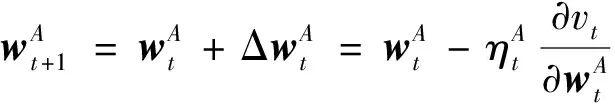
(10)

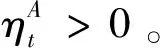
价值函数相对于动作网络权值系数的梯度计算公式为：

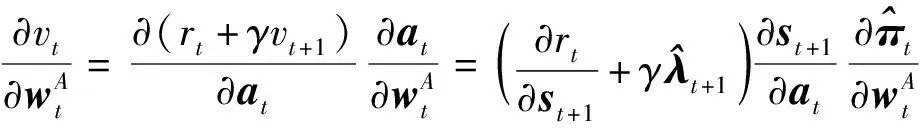
(11)

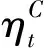
1.3 增量模型在线辨识

在增量强化学习控制律中，利用增量模型来近似非线性系统在时刻运行点(,)邻域内的模型。假设当前时刻→，基于一阶泰勒展开，得到离散的近似线性化模型为

+1≈(,)+(,)Δ+(,)Δ

(12)

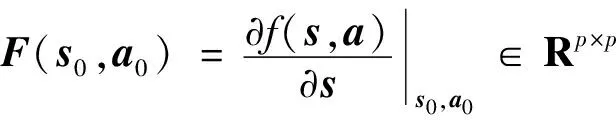
进一步，得到增量式动力学模型为

Δ+1≈-1Δ+-1Δ

(13)

其中,Δ=--1∈×1,Δ=--1∈×1分别为状态量增量和控制量增量。

在增量强化学习算法中，利用实时测量得到的状态量和控制输入数据，在线辨识状态转移矩阵和控制效果矩阵。基于辨识的增量模型来预测下一步系统状态，具体为

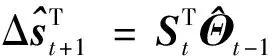
(14)

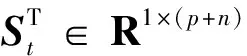
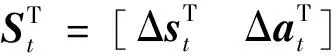
(15)

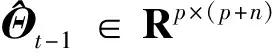
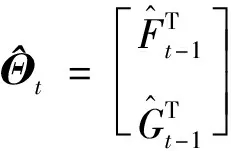
(16)

本文中参数矩阵应用参考文献[11]的递推最小二乘方法(RLS)来进行在线辨识。

进一步，可以得到式(6)和式(11)中，状态向量+1相对于上一步状态量和上一步控制量的偏导为

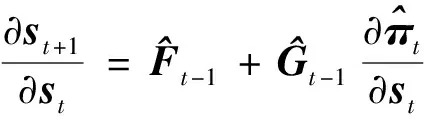
(17)

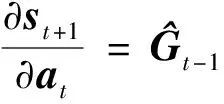
(18)

2 固定学习率增量强化学习控制实例及问题分析

以不同动压下飞行器参考攻角指令跟踪飞行控制为例来验证增量强化学习控制律，说明已有固定学习率算法存在的问题，并提出改进思路。将攻角和俯仰角速度作为系统状态，升降舵输入作为控制输入。并作如下假设：1)假设舵面偏转产生的控制力在攻角控制通道所起的作用可以忽略；2)假设飞行器机体本身产生的俯仰阻尼力矩足够小，可以忽略不计；3)假设推力与阻力平衡，由推力产生的攻角控制分量可以忽略不计。

建立飞行器纵向平面俯仰姿态运动非线性动力学模型为

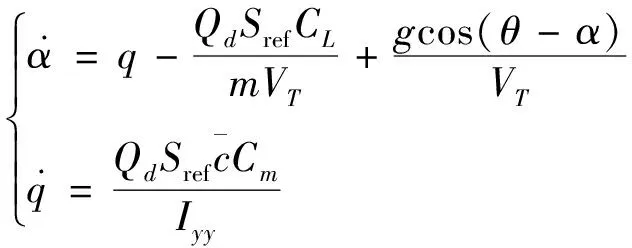
(19)

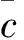
式(19)中升力系数和俯仰力矩计算公式为

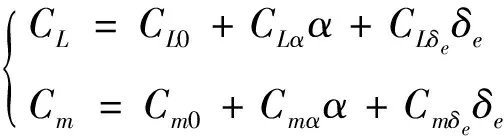
(20)

式中：0,0为零攻角升力和俯仰力矩系数;,为升力系数、力矩系数相对于攻角的偏导;,为升力系数、力矩系数相对于舵偏角的偏导。

外环采用PID控制，得到参考俯仰角速度指令：

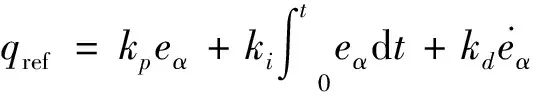
(21)

式中：=-;,,分别为比例项、积分项和微分项系数。

影响IRL算法的参考指令跟踪速度，过大的将使系统趋于不稳定，引入可以减小常值跟踪误差，有助于减弱参考指令跟踪振荡。根据PID参数调整原则，通过数学仿真确定，本文中取=188,=02,=015。

令强化学习算法中状态量、参考状态量和动作向量为

=[],=[],=[]

(22)

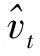
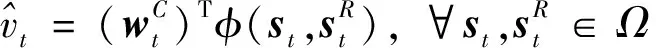
(23)

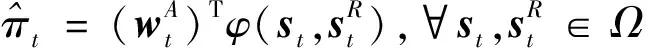
(24)

式中：函数:2→和:2→分别为选取的光滑的基底函数;,分别为评价网络与动作神经网络神经元个数，也可以选用多层神经网络结构来提高神经网络的非线性拟合能力。

为防止权值系数训练过程容易发散，选取具有有界性的双曲正切函数tanh(),∈(0, ∞]与tanh(),∈(0, ∞]组成的多项式作为评价网络和动作网络的基底函数。

=[[tanh()],[tanh()],

[tanh()]⊗[tanh()]]

(25)

=[[tanh()]⊗[tanh()]]

(26)

其中,⊗表示矩阵直积,下标,,,∈1,2,3,…,。

和的选取可以根据经验和仿真数据分析确定，从而确定神经元个数,(基底函数的总个数)和基底函数形式。神经元个数太多容易导致过拟合，太少将使拟合精度不够。因此,第一步，根据控制系统特性选取足够多的神经元;第二步，通过仿真剔除权值系数发散的神经元;从而可以确定动作网络和评价网络基底函数。本文中，取02,08,14,20,26,32;取02, 12, 24;取02, 32;取14, 26, 32。

进一步，计算得到

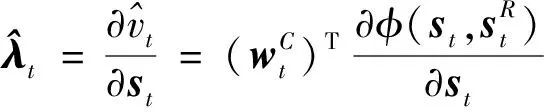
(27)

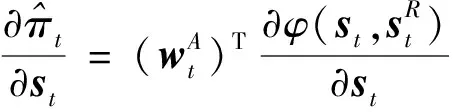
(28)

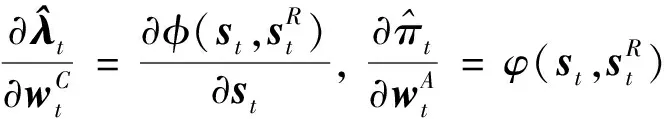
(29)

参考文献[12]，选取增量强化学习算法中的超参数，并根据经验及仿真结果，设定为常值，具体数值见表1。飞行阶段前20 s进行在线训练，在舵控指令上叠加扫频激励信号作为舵控指令，以满足充分激励(PE)条件，用于充分激励飞行器动力学模态，加快控制律学习过程和模型辨识过程。扫频信号的具体形式为：

=ej2π(+()2)

(30)

式中：初始频率取为=0.001 Hz;调制率取为=0.5。

参考文献[16]中飞行器的参数，取切换模态6下飞行器动力学参数。取回报函数权重=[50]，取任意参考攻角指令为：0～30 s 为3°，30～80 s为5°，80～120 s 为4°。初始状态取为=0, q=0，舵控指令限幅±10，飞行环境参数为0～50 s 动压为312.2 kg/(m·s)，50 s 以后动压变设为1311.2 kg/(m·s)。采用欧拉法进行数学仿真，仿真步长取为0.02 s，0～20 s 训练阶段在舵控指令上叠加扫频指令，并且动作与评价网络以较大学习率运行，以增强学习算法的探索能力，见表1，20 s以后的运行阶段调整动作网络学习率为较小值，以充分利用已学习到的经验。

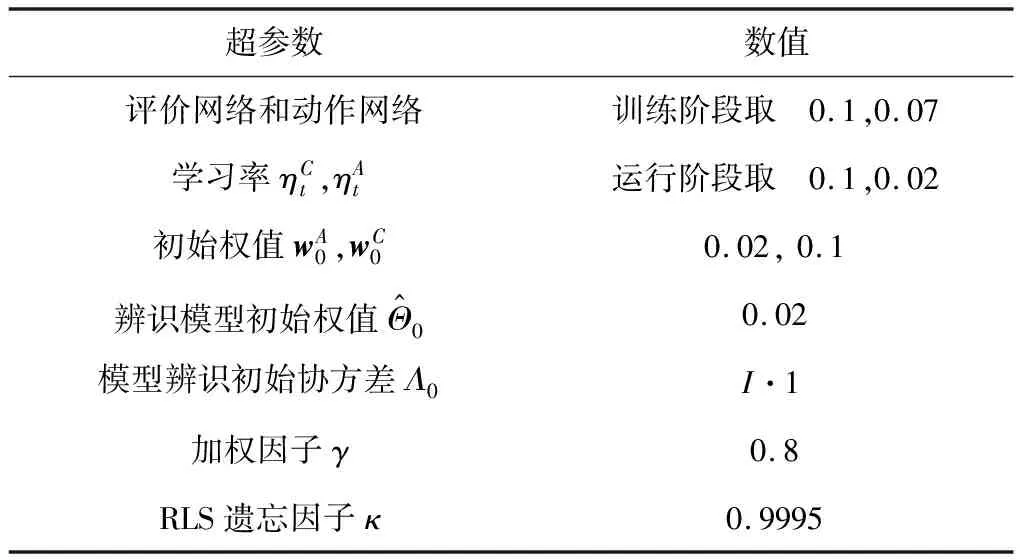
表1 超参数设定值

仿真结果如图2-3所示，可得到以下几点结论：

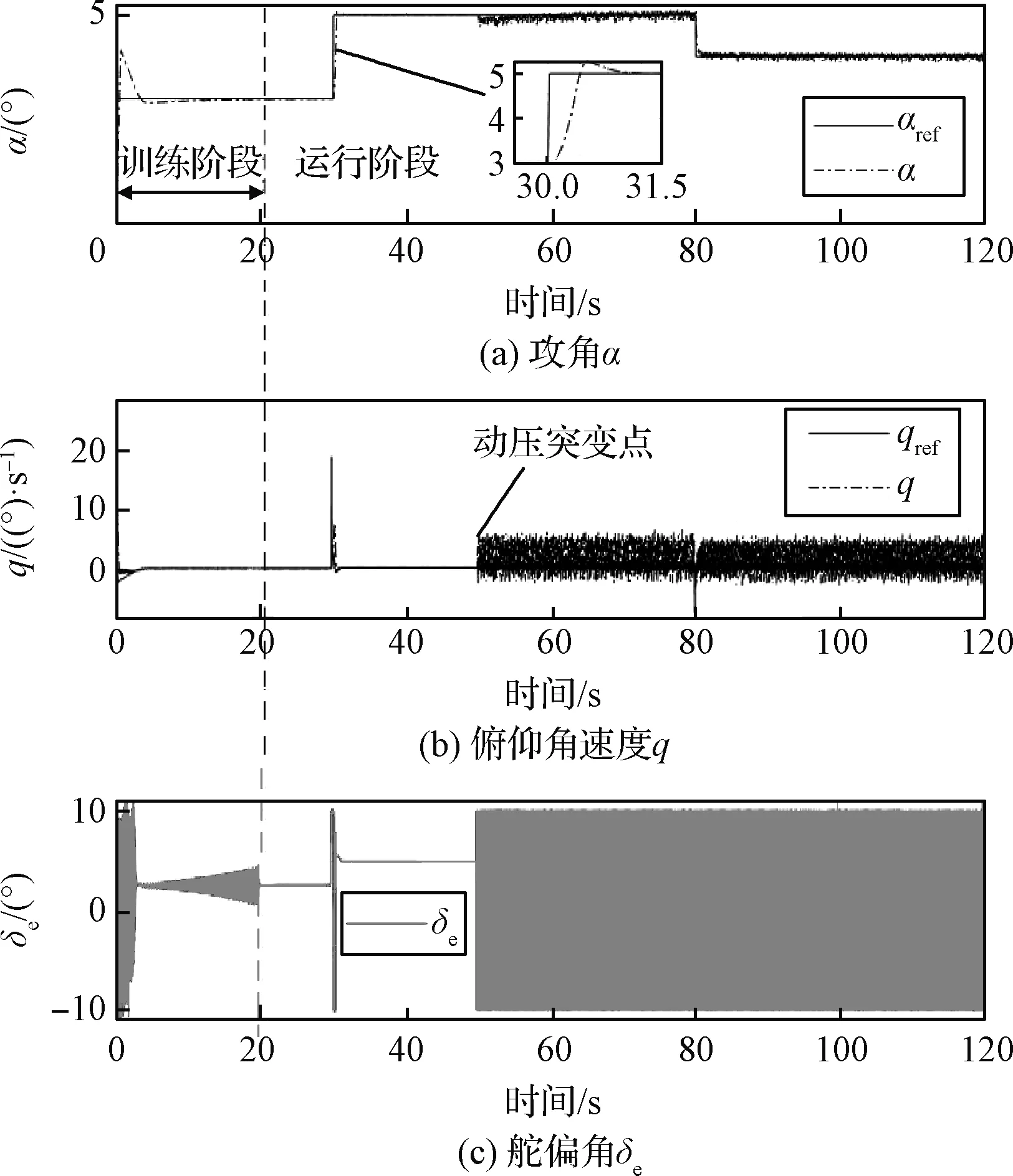
图2 固定学习率下飞行控制效果图

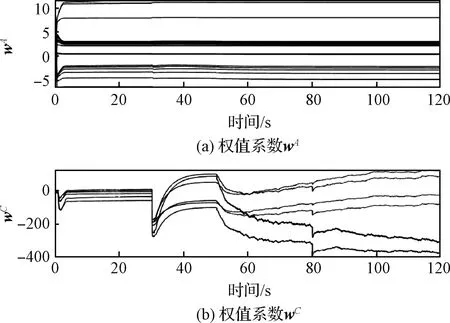
图3 固定学习率下评价网络与动作网络权值系数收敛结果

1)在20 s内的训练过程中，评价和动作网络权值系数较快收敛；

2)运行阶段，飞控能够跟踪不同于训练时刻的参考攻角指令；

3)在飞行器动压变化较大的情况下，基于预先设定学习率参数会导致IRL控制算法失效，评价网络权值系数发散。

3 增量强化学习控制器自适应学习率设计

飞行控制系统的稳定性可以通过观察飞行状态的振荡情况来进行分析，工程上通常采用阶跃响应振荡次数来作为飞行控制器设计输入。因此，本文的思路是实时监测飞行状态跟踪误差的振荡情况，根据飞行状态振荡程度迭代优化行动网络学习率超参数。基于性能监测的自适应学习率增量强化学习算法的结构如图4。本文改进的自适应学习率调整部分用于在线优化调整学习率参数。

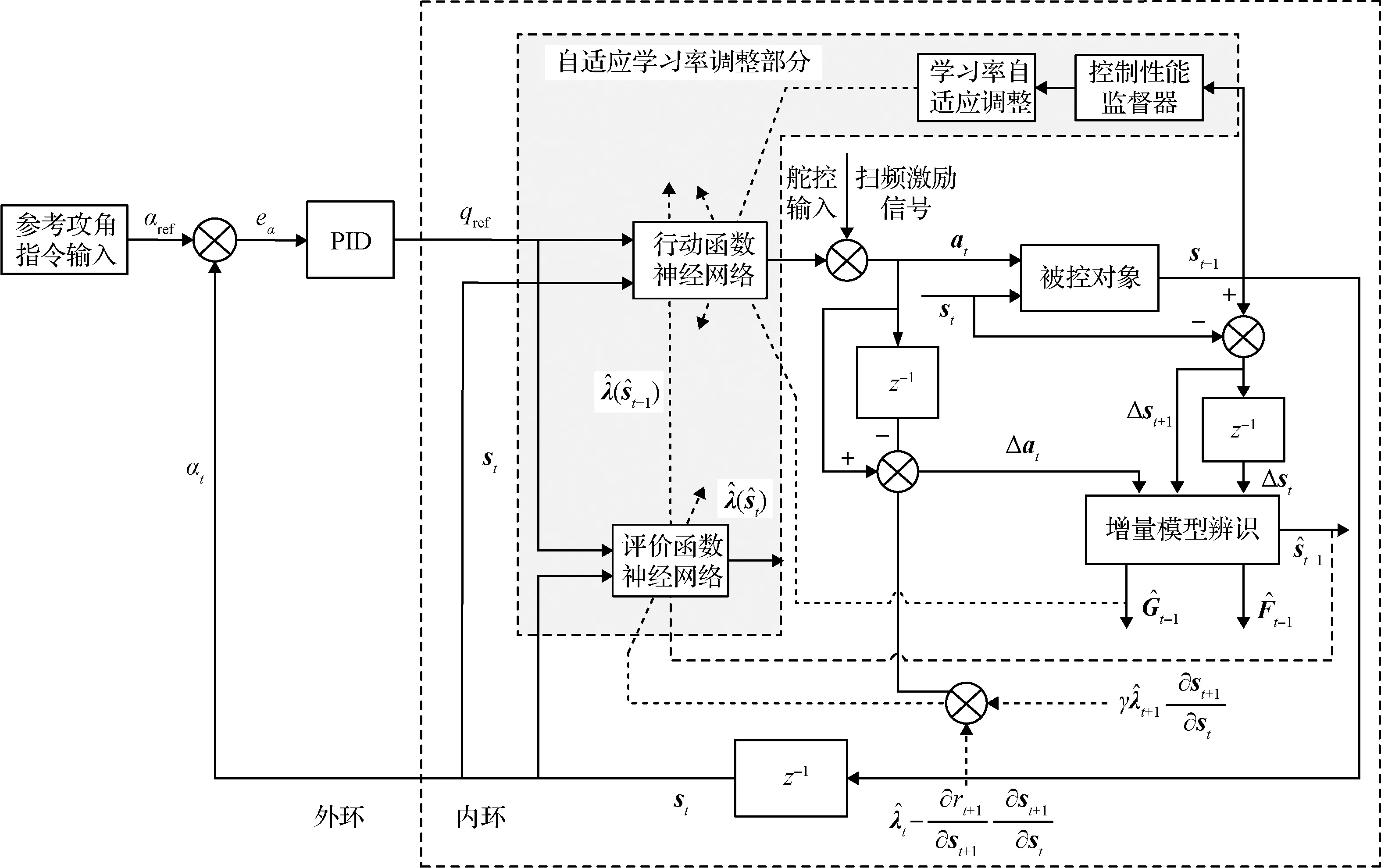
图4 自适应学习率增量强化学习算法框架(实线表示前向信号流，虚线代表自适应调整路径)

3.1 基于小波分析的状态信息振荡程度监测

小波分析是在20世纪80年代Morlet、Arens、Grossmannn等的研究基础上发展起来的应用数学领域成果。复Morlet小波在时频两域均具有良好的辨别能力，复Morlet小波母函数具有随频率参数改变而自动调节时、频分辨率的能力，在频域内，可将其视为一个窄带滤波器。本文利用其特性，分析评估飞行控制性能。

：在平方可积的实数空间()，即能量有限的信号空间中，设()∈()，其傅里叶变换为()，若()满足如下容许性条件：

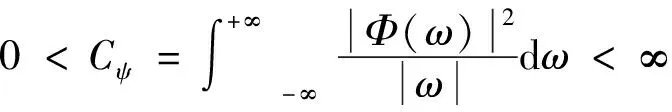
(31)

则称()为基本小波或母小波。

将基本小波()经过伸缩和平移后，便可以得到小波函数族：

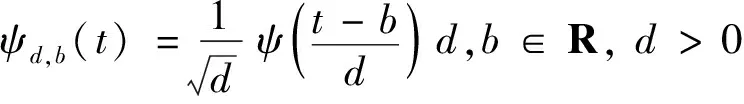
(32)

式中：为伸缩因子;为平移因子。

给定任意平方可积信号()，即()∈()，则经过小波变换后，得到

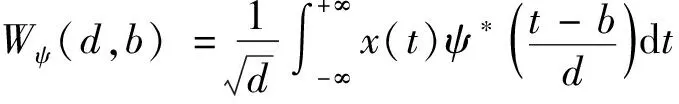
(33)

式中：()为小波函数()的复共轭;(,)称为小波变换系数。

在时域和频域范围内，复Morlet小波函数的定义如式(34)和式(35)。

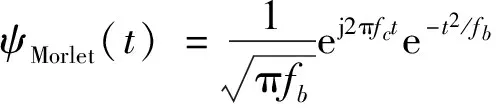
(34)

()=eπ(-)

(35)

式中：为中心频率;为带宽，需要根据实际信号特性来确定这两个参数。

飞行状态的振荡幅值及振荡次数反映了飞行控制系统的稳定性和稳定裕度。基于此思路，本文利用小波分析强大的时频分析能力，以俯仰角速度跟踪误差为输入，在线分析计算不同学习率下飞行器稳定性指标，然后基于梯度下降法迭代更新增量强化学习飞控算法的学习率。

3.2 动作神经网络学习率自适应调整策略

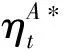
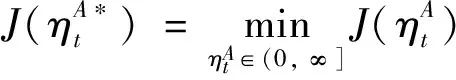
(36)

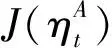
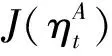
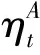
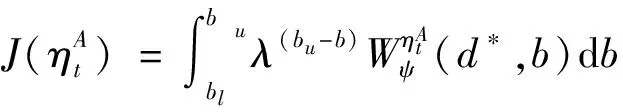
(37)

式中：，为小波分析输入信号的起始和终止时刻;0<<1为遗忘因子，用于增大靠近当前时刻的小波系数权值。

式(37)中为小波系数取最大值时所对应的频率值，计算公式为

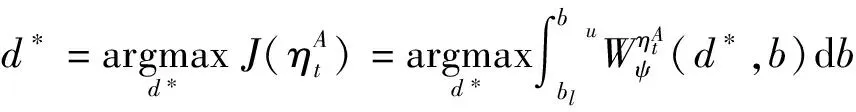
(38)

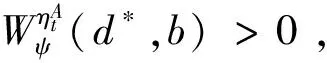
得到飞控系统稳定度评估指标后，基于梯度下降法设计学习率的更新率

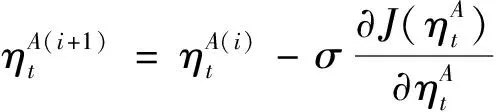
(39)

式中：上标+1表示第+1步;为更新率步长。

.

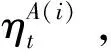
1)设置小波分析时间窗口Δ及学习率更新容许误差；

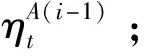
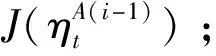
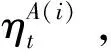
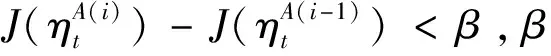
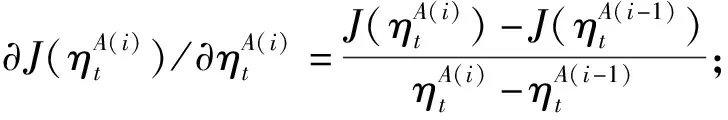
7)利用式(39)的更新率计算得到第步的学习率参数；

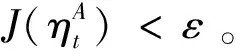
步骤5设置阈值主要是为了防止小波误差引起的学习率频繁更新。

4 仿真校验

在这一部分，将采用第二节提到的飞行器非线性模型及不同仿真条件来验证文中提出的自适应学习率的增量强化学习控制算法。

4.1 基于小波分析的控制器稳定性指标合理性校验

通过数学仿真对比分析固定学习率和自适应学习率下小波分析结果，校验控制系统稳定性小波分析的合理性。采用本文第二节中相同的仿真条件，在50 s时飞行器的动压突变，动作网络学习率为0.02和自适应学习率情况下小波系数如图5和图6所示。图5a和图6a分别为固定学习率和自适应学习率下小波系数图，图5b和图6b分别为式(38)最大小波系数对应频率下的小波系数。分析可知，固定学习率下小波系数在频率4 Hz附近取值最大，并且随着时间变化基本不衰减，而在自适应学习率下小波系数较小，并且衰减很快。图5和图6对应的时域轨迹曲线分别如图2和图7所示。对比分析可知，基于小波系数建立的评价函数能有效反映控制系统振荡程度，为控制系统稳定性实时评价提供性能指标。

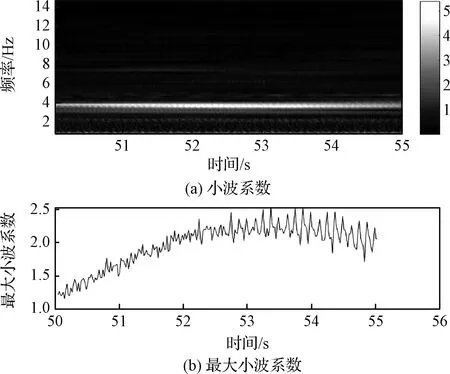
图5 固定学习率下小波系数图

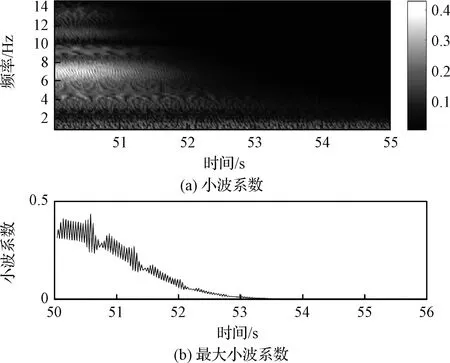
图6 自适应学习率下小波系数图

4.2 ALRIRL与IRL算法对比

A.动压大范围变化下算法对比

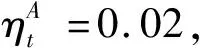
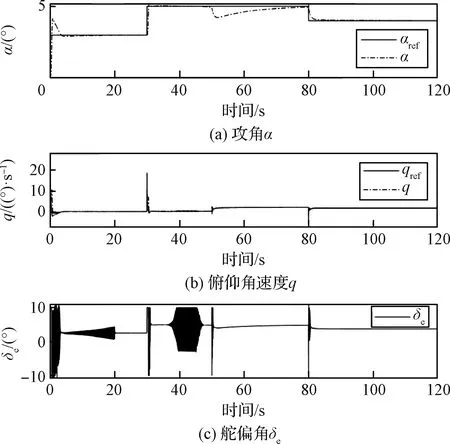
图7 自适应学习率下飞行控制效果图

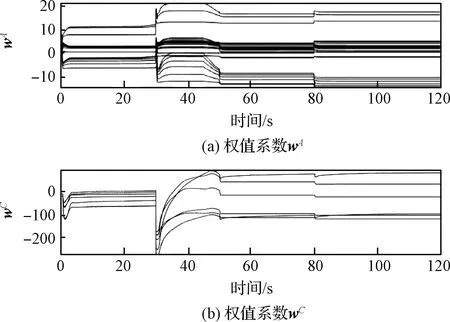
图8 自适应学习率下权值系数收敛结果

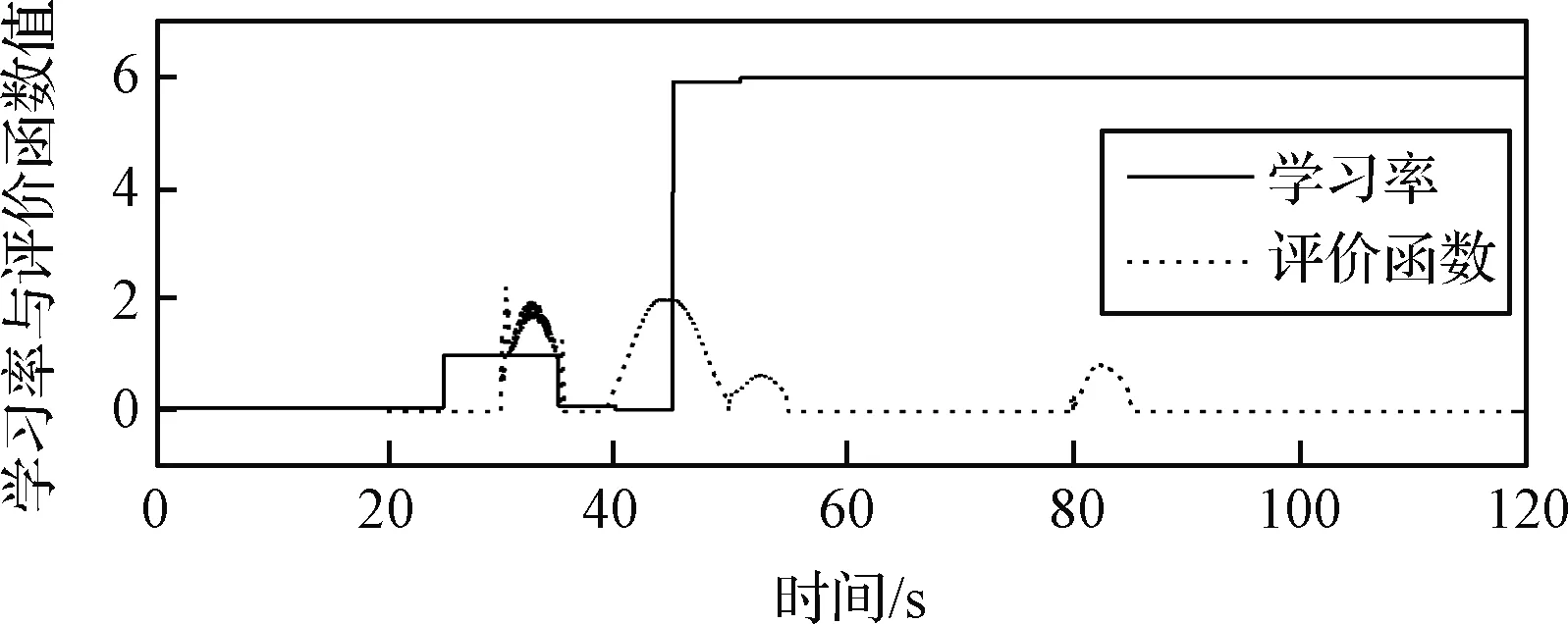
图9 自适应学习率与评价函数变化结果

B.ALRIRL与IRL算法稳定性对比

学习算法的收敛性和稳定性对于评估在线学习算法至关重要。目前，基于强化学习的飞行控制算法稳定性还没有得到严格的证明。本文中采用常用的蒙特卡洛打靶法来评价控制器收敛效果。利用运行阶段(仿真时间大于20 s为起始到仿真结束)回报函数式(3)的累积值来衡量控制器的性能。采用与上一节相同的仿真条件，而初值,随机生成，运行仿真程序。如果一次运行的累计回报值超过4000则认为此次控制失败，并进行标记。一次运行累计回报值4000对应俯仰角速度常值误差为≈0.89°。

随机生成初始状态,∈([-6 6],[-8 8])，运行100次仿真，统计累计回报值来评价学习算法的稳定性。在随机初始状态下，ALRIRL与IRL算法的累计回报值统计结果对比如图10-a所示。由仿真结果可知，ALRIRL算法下，累计回报值分布区域更小，大部分在2000以内，成功率由IRL的88%提高到99%，较大提高了学习算法的稳定性。

飞行器飞行动压在50 s随机变化，变化范围为1.4～4.2倍，运行100次仿真，统计累计回报值来评价学习算法的稳定性。ALRIRL与IRL算法的累计回报值统计结果对比如图10-b所示。由仿真结果可知，随机动压变化下，ALRIRL算法累计回报值更小，大部分在2000以内，成功率由IRL的0%提高到100%，大大提高了学习算法在动压突变情况下算法稳定性。

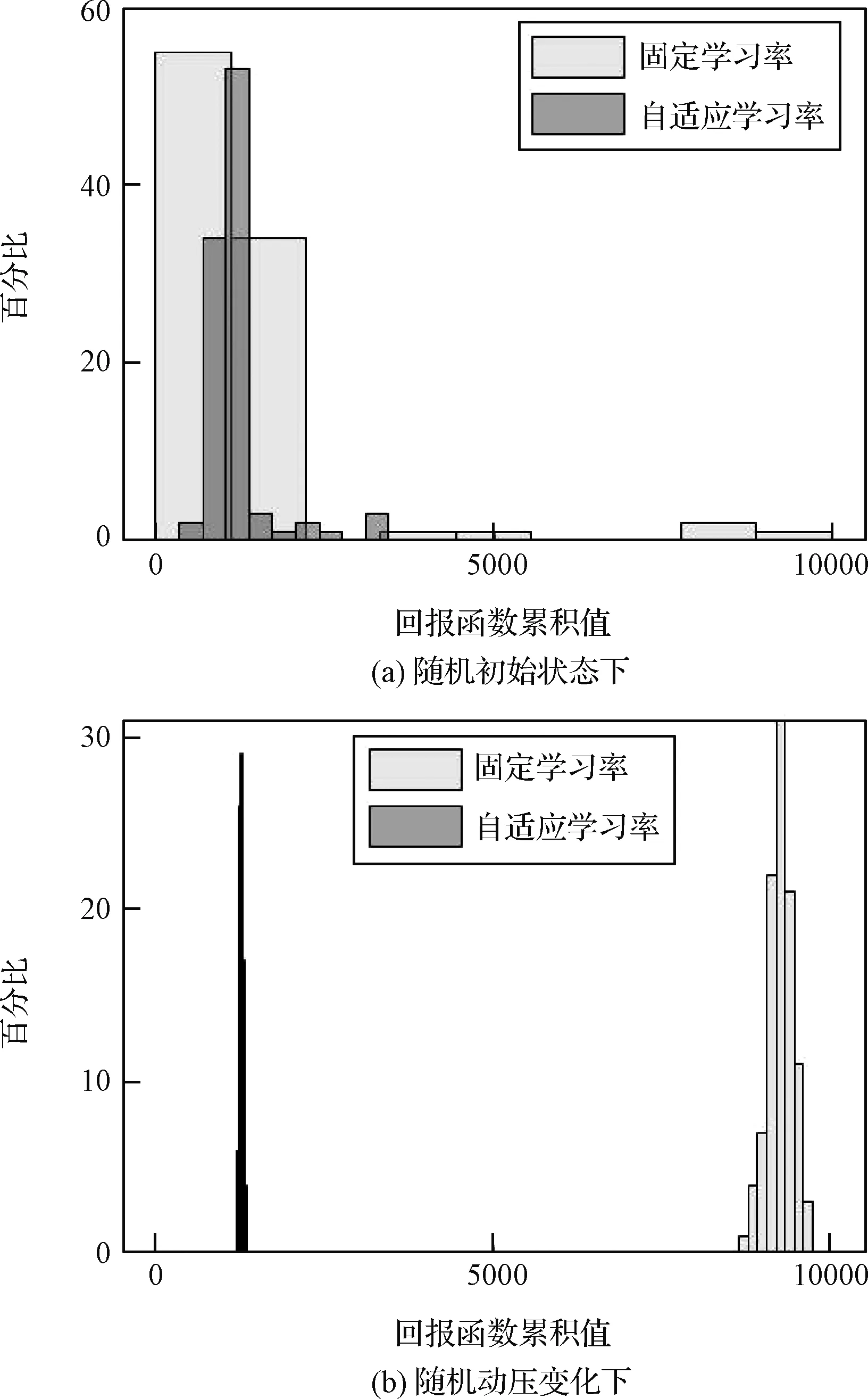
图10 ALRIRL与IRL算法累计回报值直方图

5 结 论

对于预先设定动作网络学习率参数的IRL方法飞行控制失败率较高，并且无法适应飞行器动力学参数大范围变化情况下的姿态稳定控制问题，本文提出利用小波分析方法在线监测IRL飞行姿态控制稳定度，基于梯度下降法在线自适应调整增量强化学习控制器学习率的方法。仿真实例表明，通过小波变换设计的飞行控制稳定度评价指标能够有效地反映飞控系统的稳定度。利用梯度下降法在线优化调整学习率参数快速有效。本文提出的ALRIRL飞行控制律能够有效提升强化学习飞行控制算法在随机初值及随机动压变化下的飞行成功率，减轻了强化学习飞行控制算法对于精确学习率参数的依赖。