天问一号着陆器大底分离触发条件设计方法

田 阳，陈 正，崔祜涛，黄翔宇，饶 炜，董 捷

(1.哈尔滨工业大学深空探测基础研究中心，哈尔滨 150001；2.北京控制工程研究所，北京 100094；3.北京空间飞行器总体设计部，北京 100094)

0 引 言

为确保着陆器能够安全降落在火星表面，火星着陆任务一般采用进入、下降和着陆(Entry，descent and landing，EDL)策略，如NASA成功实施的火星探测器，海盗号(Viking)、火星探路者(Mars pathfinder,MPF)、火星探测漫游者(Mars exploration rover,MER)、凤凰号(Phoenix)和火星科学实验室(Mars science laboratory,MSL)等。我国火星探测任务“天问一号”也采用了类似的方法，在进入段完成初步减速后，展开降落伞进一步将着陆器减速至亚声速，然后降落伞与着陆器分离，实施最后的着陆操作。

伞降过程中防热大底分离和背罩分离是比较关键且容易发生风险的阶段。防热大底外形为钝锥角球锥，安装在着陆器前端，如图1所示，通过火工品作用使其脱离着陆器。在分离过程中，当气流经过防热大底时，在其背后形成尾流区，背罩及内部的着陆平台处于防热大底的尾流区当中，由于回流的作用产生吸力，这种作用可能使防热大底的气动减速度大于背罩和着陆平台的减速度。另一方面，降落伞喘振等因素使着陆器姿态发生摆动，与防热大底形成相对姿态运动。这两方面原因造成分离过程存在防热大底碰撞背罩或着陆平台的可能性，威胁着陆平台安全。

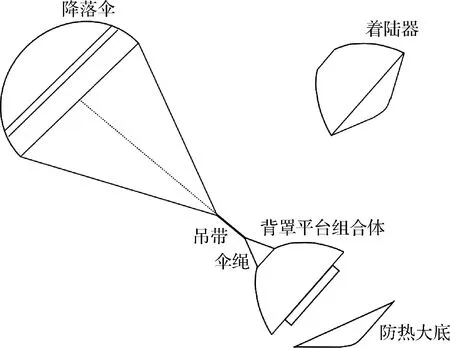
图1 火星着陆器模型

美国在火星探测器防热大底分离方面展开过很多研究，文献[10]介绍了针对海盗号防热大底分离过程的风洞试验，文献[11]进一步对试验的数据及结果展开了深入分析，并且仿真计算了分离动作弹簧弹力与分离时间之间的关系。国内学者在火星探测EDL技术方面也开展了相关研究，主要包括EDL方案综述及关键技术分析，进入段制导控制策略研究，以及防热大底、背罩和降落伞气动特性研究等。综合国内外研究现状，目前尚未见到针对防热大底分离安全性展开深入分析或确定分离触发条件的研究成果。

本文根据中国火星探测任务“天问一号”总体及控制系统设计的需求，研究防热大底与着陆器相对运动特性，量化分析造成防热大底碰撞的因素，给出无碰撞分离的触发条件确定方法。

1 火星着陆器模型

根据着陆器总体结构和伞降过程研究需要，将伞降阶段着陆器模型分为以下几个部分。

着陆器由防热大底、背罩及其内部的着陆平台组成。在防热大底分离后，着陆平台仍与背罩刚性连接，因此在研究中将背罩与着陆平台组合体视为单刚体，下文简称背罩平台组合体。

背罩通过四根伞绳与降落伞吊带末端连接，伞绳模型为带有速率阻尼的弹簧模型。

为了便于研究，在完成弹出和充气等动态过程后，将降落伞至吊带末端的结构视为刚体建立动力学模型。

2 防热大底分离后长期运动趋势分析

防热大底在火工品作用下与着陆器分离后，受到气动力、气动力矩和火星引力的作用，与着陆器产生相对平动运动和旋转运动，这两种运动都可能使防热大底再次接触着陆器并发生碰撞，影响着陆器的安全性。这里首先分析防热大底在气动力及引力作用下相对速度的长期变化趋势，确定防热大底分离后可能再次接触着陆器的可能区间，为进一步分析确定安全分离条件奠定基础。

由于降落伞、背罩平台组合体及防热大底的气动参数存在一定的偏差，在分析过程中需要确定最不利于分离的仿真参数偏差情况，建立防热大底分离恶劣仿真条件。显然当防热大底阻力系数偏差为上限、降落伞和背罩平台组合体阻力系数取下限值，不利于防热大底分离。同时，考虑到马赫数对气动力的影响，分离时刻速度越大，气动力作用越强，越不利于分离，因此给出如表1所描述的分离仿真条件，并在该条件下仿真分析防热大底分离后的相对速度。

表1 防热大底分离恶劣仿真条件

利用降落伞、背罩平台组合体以及防热大底六自由度数学模型仿真分离后的运动状态，背罩平台组合体以与防热大底相对速度结果如图2所示。

图2 防热大底与背罩平台组合体相对速度

由于在马赫数0.8到1的区间内，马赫数效应因子(MEF)值较小，意味着在这个速度区间内降落伞受到的气动阻力较小，导致大底分离更加困难。因此仿真主要对分离触发马赫数0.8到1的弹道进行分析，这里分离触发马赫数即分离时刻着陆器的速度。

图2所示曲线由左到右分别对应分离马赫数为1.0、0.99、0.98、……、0.8的相对速度时间历程，在防热大底开始分离但未脱离导轨过程中，由于火工品推力作用，防热大底相对背罩平台组合体速度迅速增大。脱离导轨后，分离触发马赫数大于0.91的弹道，其相对速度出现减小趋势，但防热大底下降速度仍比背罩平台组合体下降速度大。

根据不同分离马赫数的仿真结果可以看出，分离后防热大底长期运动趋势是加速远离背罩平台组合体，最易发生碰撞的阶段是防热大底脱离导轨最初的数秒内，此时相对距离较小且与相对姿态运动耦合，防热大底最有可能再次接触背罩平台组合体。

3 防热大底分离后短期运动与安全性关系分析

防热大底短期分离是指火工品推力作用于防热大底使其沿导轨运动，直至防热大底与背罩平台距离大于数倍防热大底直径的过程。沿导轨分离阶段受到导轨约束和火工品推力作用，防热大底不会与背罩平台组合体发生碰撞。而脱离导轨后，防热大底与背罩平台组合体独立运动，若两者有较强的相对姿态运动，且两者距离较小则可能发生碰撞。

事实上，脱离导轨瞬时防热大底和背罩平台组合体具有相同的姿态和角速度，相对姿态运动产生的原因除了气动力矩的差别之外，主要是降落伞伞绳力矩。为了说明这一问题，首先通过典型弹道仿真数据阐述伞降段姿态运动基本规律。

3.1 伞降段着陆器姿态运动规律

利用着陆器和降落伞组合体六自由度动力学模型，根据伞降段标称弹道条件及气动参数进行了仿真，姿态运动及伞绳力结果如图3至图5所示。

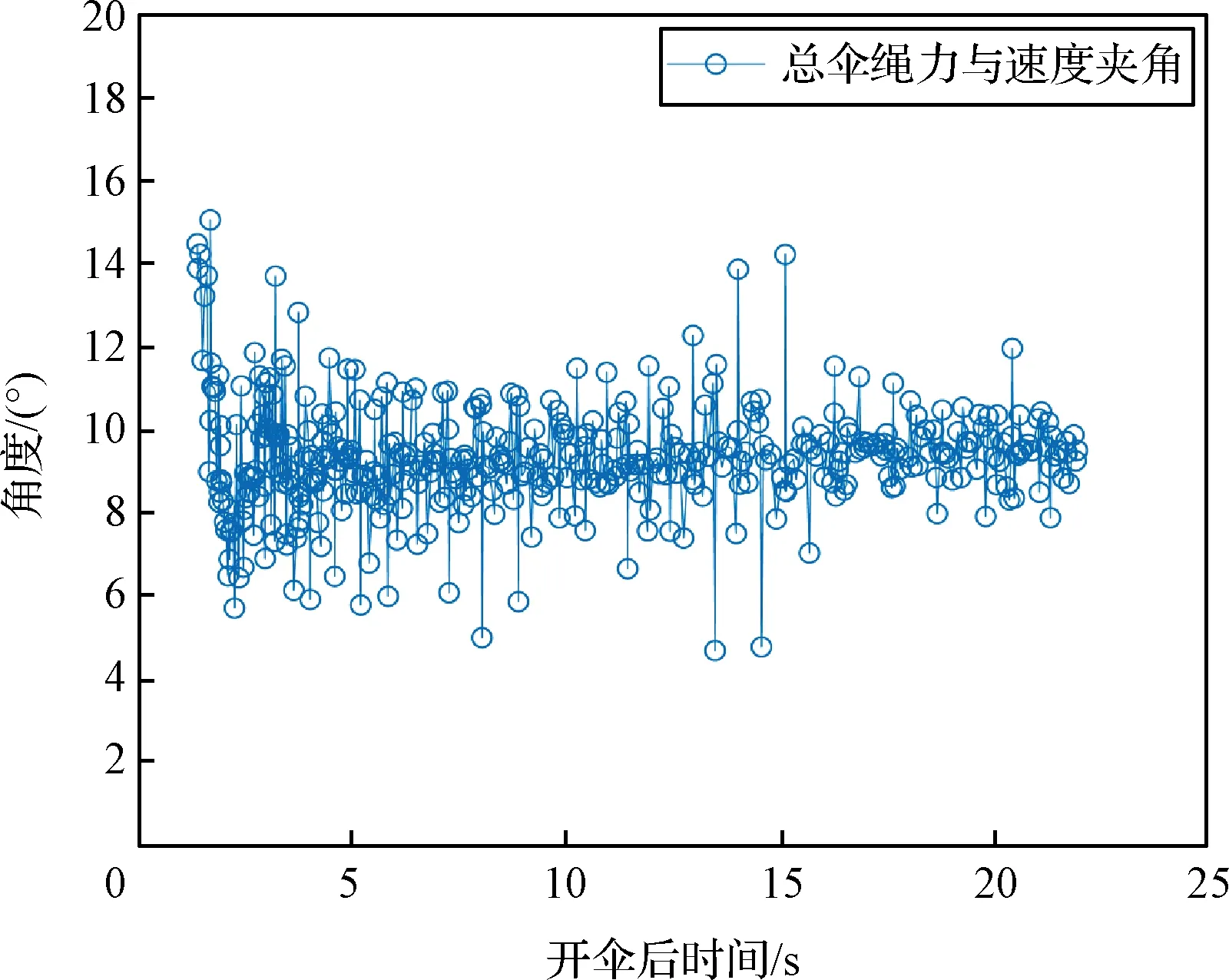
图3 总伞绳力方向与着陆器速度方向夹角

图4 总伞绳力在着陆器弹道系中的三轴分量

图5 着陆器姿态及总伞绳力在着陆器弹道系下的方向角

图3给出了降落伞弹出后，总伞绳力方向与着陆器速度矢量夹角曲线。结合图5中总伞绳力矢量在着陆器弹道系下的方向角(俯仰及偏航方向)结果，可以看出降落伞作用在着陆器上的总伞绳力方向绕着陆器速度方向缓慢旋转，且与着陆器速度方向夹角约等于降落伞平衡攻角。图5还给出了着陆器姿态运动特点，根据着陆器攻角和侧滑角变化规律，说明着陆器在伞绳力矩的作用下快速摆动，且平衡位置(平衡方向)近似为总伞绳力方向。

防热大底分离后，背罩平台组合体姿态同样快速摆动，因此产生相对姿态运动。

3.2 相对姿态运动对安全性影响分析方法

伞绳力矩使背罩平台组合体姿态按照近似正弦规律摆动，在分离高度、马赫数等条件固定的条件下，防热大底脱离导轨瞬时背罩平台组合体姿态摆动相位，以及短期分离过程中的峰值角速度将决定后续的相对姿态运动。因此需要首先分析这两个因素与分离安全性之间的关系。

首先定义描述分离安全性的定量指标，防热大底与背罩平台组合体最近距离(以下简称最近距离)。该最近距离是指防热大底与背罩平台组合体外包络形状距离的最小值。在仿真分析过程中，通过以下策略近似计算最近距离。设置由背罩平台组合体质心均匀射出若干射线，每条射线分别与防热大底和背罩平台组合体外包络形状相交，射线起点到两个交点距离差为射线方向上的距离，全部距离最小值为防热大底与背罩平台组合体最近距离。当最近距离小于或等于0时表明发生碰撞。显然在整个分离过程中，最近距离的极小值越大，分离安全性越高(如图6所示)。

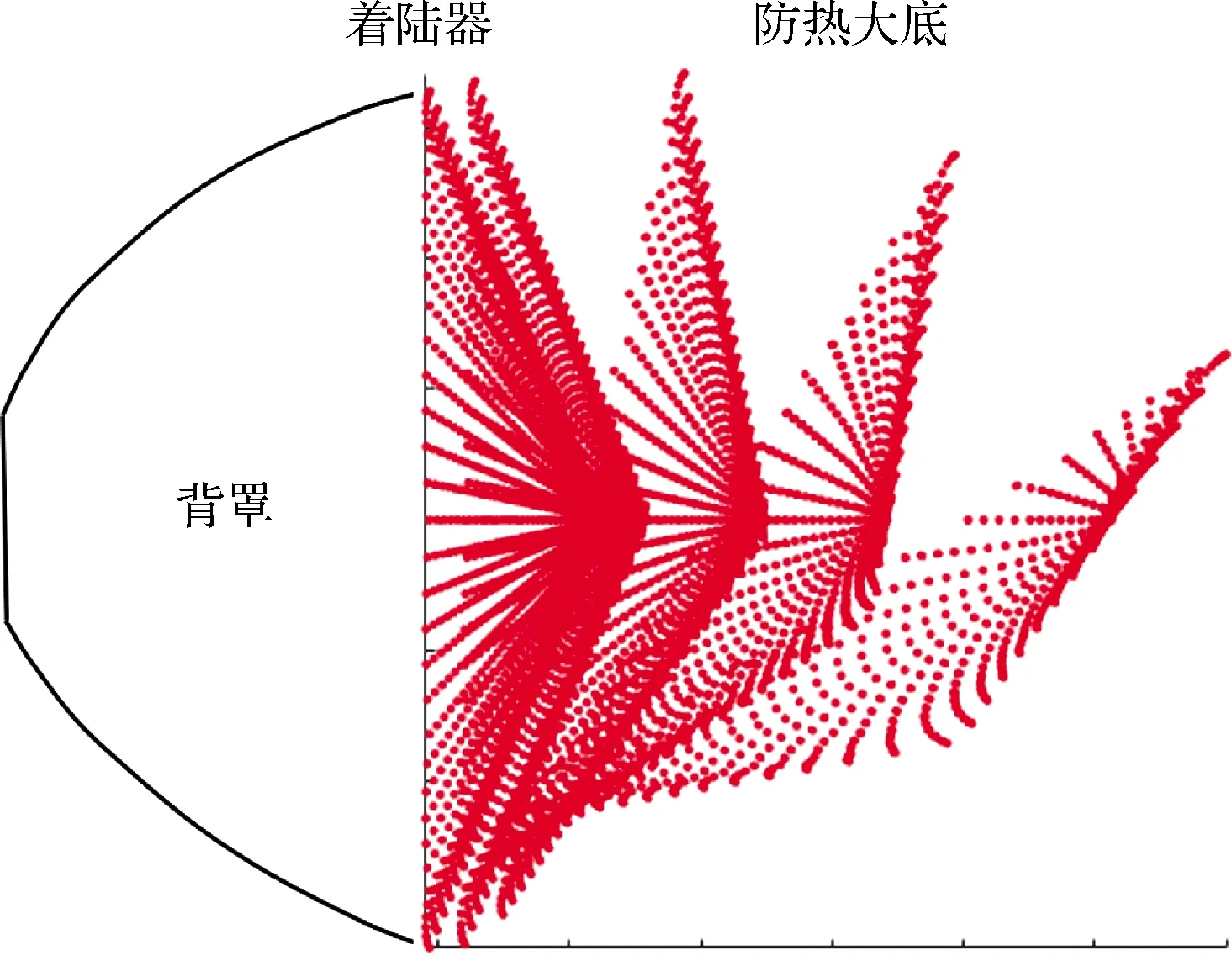
图6 射线与防热大底交点

为了定量地给出不同峰值角速度和姿态摆动相位与最近距离关系，我们将背罩平台组合体、伞绳吊带以及降落伞构成的复杂多体动力学问题转化为背罩平台组合体单刚体动力学分析问题，建立一种近似分析模型，解决完整多体模型难以根据分析需要设定系统状态的问题。例如，完整多体模型在给定背罩平台组合体姿态和角速度后，降落伞姿态及角速度由于缺乏约束而难以确定。下面给出分析模型建立的主要思路。

根据图4给出的总伞绳力时间历程曲线，充气等动态过程结束后，总伞绳力大小基本保持稳定。另外根据图5所示的着陆器弹道系下总伞绳力方向角时间历程曲线，总伞绳力方向变化周期约为20 s，分析短期分离相对姿态运动可以忽略降落伞质量，并假设总伞绳力为一恒定矢量，其大小由背罩平台组合体马赫数及降落伞气动系数计算。

给定总伞绳力大小和方向条件下，总伞绳力对背罩平台组合体产生的力矩按照以下方法计算。

如图7(a)所示，背罩通过四根伞绳与降落伞连接。当伞绳全部拉直时，总伞绳力作用点为伞绳汇交点。在背罩平台组合体摆动过程中，可能出现部分伞绳松开的状态，此时总伞绳力作用点需要根据总伞绳力在背罩平台组合体本体系下方向具体分析。

假设总伞绳力矢量的反向延长线与背罩上伞绳连接点，，和构成的平面相交于点，如图7(a)所示，显然当位于以，，，为顶点的矩形内部时，有3或4根伞绳拉直，总伞绳力力臂可以根据伞绳汇交点位置计算。当点位于其它区域时，可能有1或2根伞绳拉直，具体拉直数量如图7(b)所示。1根伞绳拉直情况下，总伞绳力作用点为拉直伞绳连接点。2根伞绳拉直情况下，每根伞绳上的力按照矢量分解规则确定，作用点为对应的两个伞绳连接点。

图7 总伞绳力方向与拉直伞绳数量关系

图8 分析模型俯仰偏角、偏航角速度仿真结果

给定总伞绳力大小和方向，可以根据上述规则计算总伞绳力产生的力矩，并进一步根据角速度和摆动相位分析计算背罩平台组合体的姿态运动。

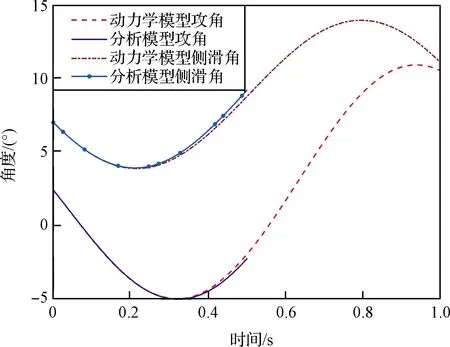
图9 分析模型攻角、侧滑角仿真结果

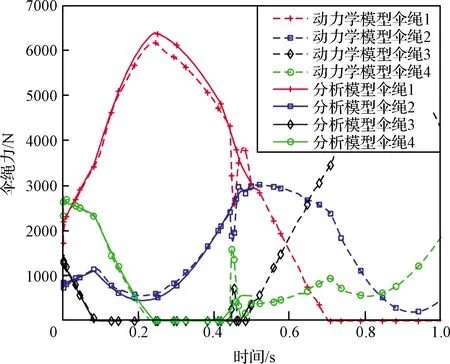
图10 分析模型伞绳力仿真结果

为了验证该分析模型的正确性，利用典型弹道数据与分析模型仿真结果进行了比较，结果如图8至图11所示。可见在防热大底脱离导轨后的0.5 s内，分析模型与完整多体模型仿真的背罩平台组合体运动状态基本相同，角速度误差小于2(°)/s，姿态误差小于0.2°。说明分析模型可以在简化模型复杂程度的情况下准确模拟分离时的相对运动状态。

图11 分析模型背罩平台组合体位置仿真结果

3.3 分离相位与最近距离关系分析

利用分析模型确定背罩平台组合体摆动相位对最近距离的影响，首先需要确定摆动相位与角速度的对应关系。图12给出了背罩平台组合体俯仰角速度和攻角关系。可见角速度的峰值与攻角的平衡状态对应，角速度的平衡状态与攻角的峰值对应。由图中数据可知，初始角速度为120(°)/s时攻角的极大值为4.367°，极小值为-19.96°。以此为基础，设定四个防热大底分离相位，见表2，分别为角速度下限、平衡攻角；角速度为0(°)/s、下限攻角；角速度上限、平衡攻角；角速度为0(°)/s、上限攻角。对应背罩平台组合体的姿态运动状态分别为：向下摆动至平衡攻角且角速度达到峰值；向下摆动至极限负攻角处且角速度为0(°)/s；向上摆动至平衡攻角且角速度达到峰值；摆动至极限正攻角处且角速度为0(°)/s。

图12 俯仰角速度与攻角的相位关系

表2 分离相位(铅垂面内摆动)

根据设定的四个防热大底分离相位，利用分析模型计算对应的最近距离，如图13所示，当背罩平台组合体于平衡攻角处并向上旋转时分离，防热大底与背罩平台组合体最近距离最小，发生碰撞的可能性最大。

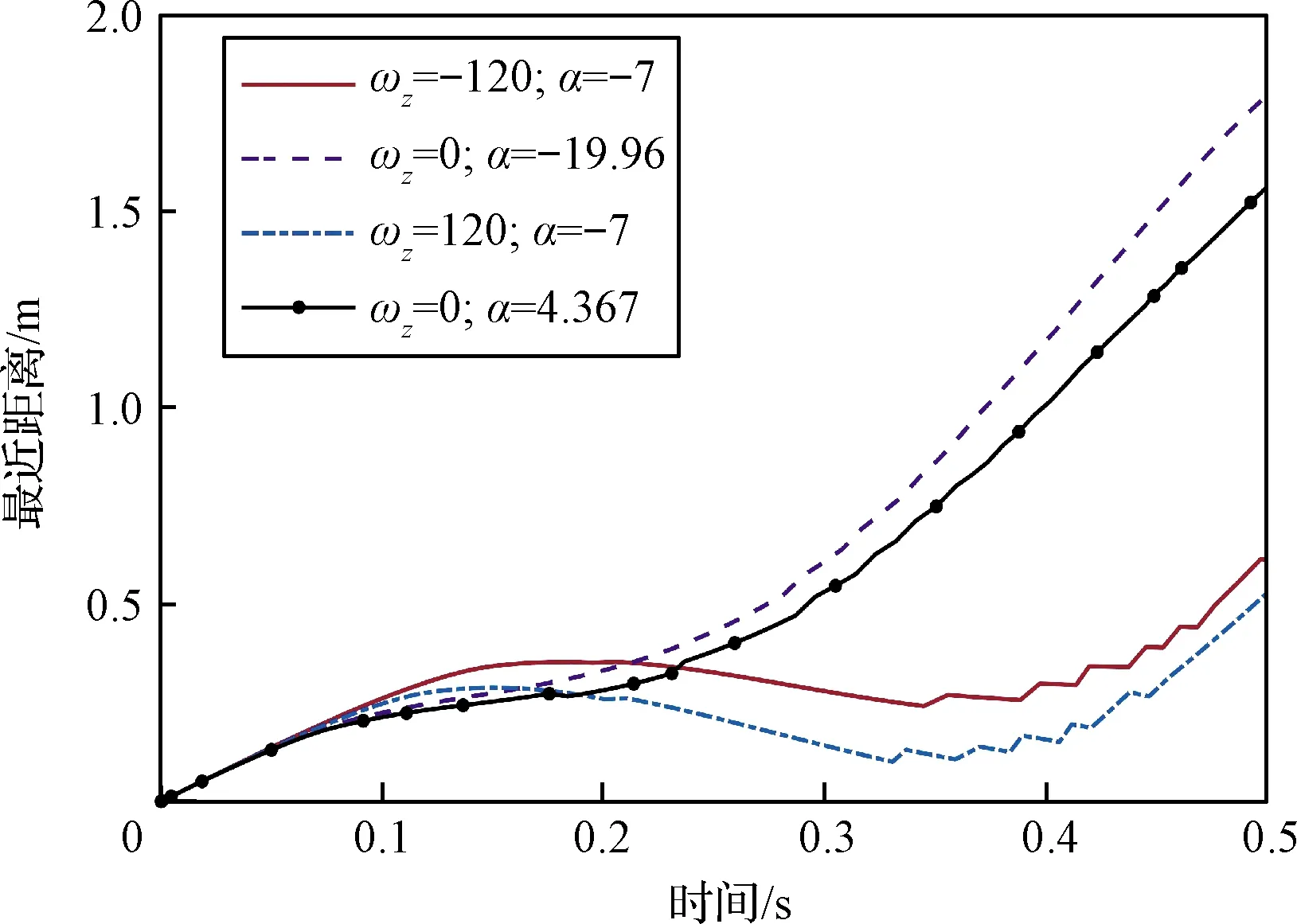
图13 不同分离相位对应的最近距离(铅垂面内摆动)

以上分离相位对最近距离影响的分析只考虑了背罩平台组合体在铅垂面内摆动的情形，下面利用相同的方法对水平面内摆动的情况进行分析。

水平面内分离相位与最近距离关系的仿真结果如图14所示，当背罩平台组合体处于平衡侧滑角时分离，防热大底发生碰撞的可能性最大。

表3 分离相位(水平面内摆动)

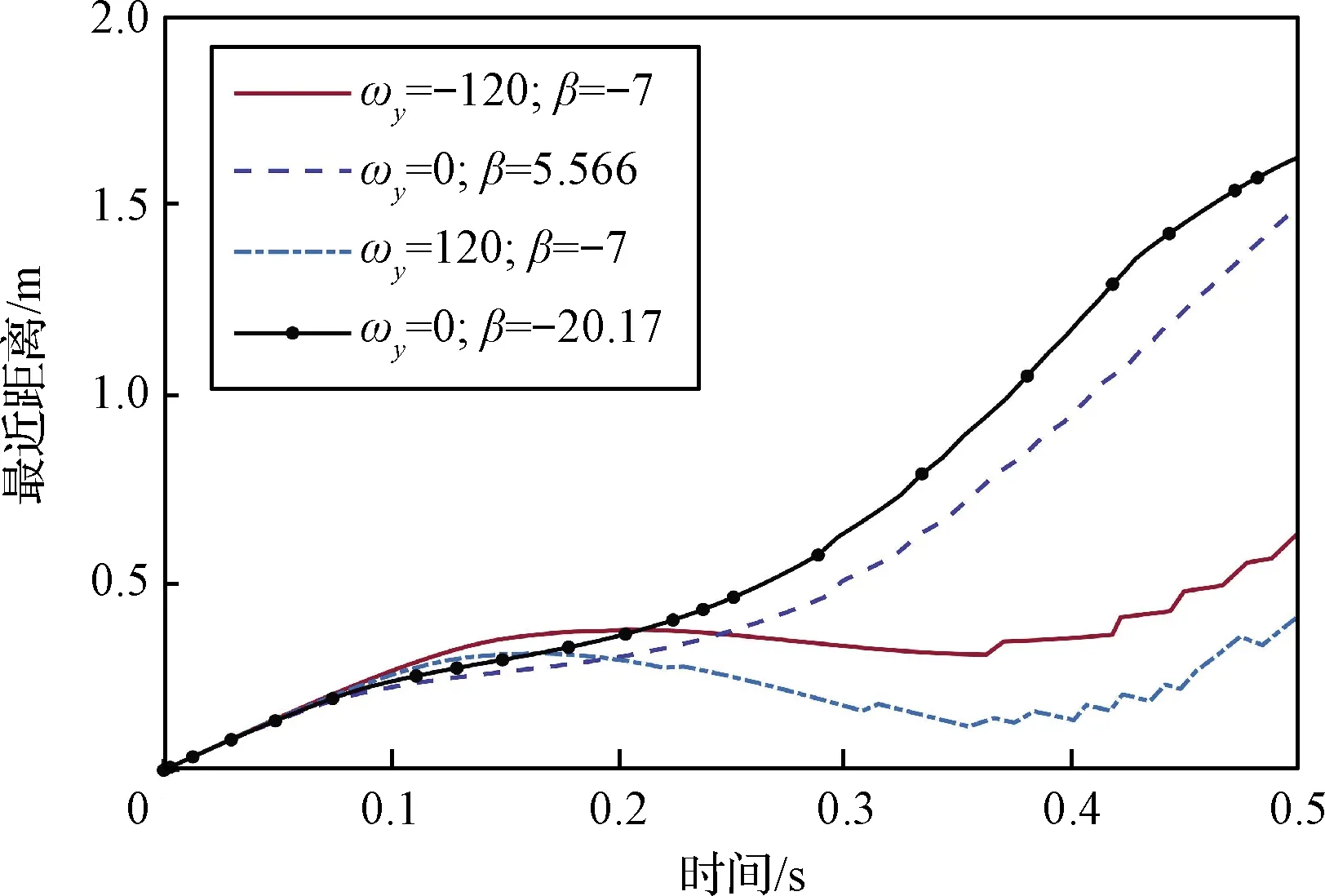
图14 不同分离相位对应的最近距离(水平面内摆动)

根据铅垂面和水平面内对分离相位的分析可知，当背罩平台组合体处于平衡位置时，防热大底分离的危险性最高。因此在三维空间中分析分离相位与最近距离关系时，将背罩平台组合体处于平衡位置视为危险相位，在此基础上分析俯仰与偏航两个方向运动对防热大底分离安全性的影响。为保证对比合理性，给定背罩平台组合体俯仰和偏航两轴合角速度为120(°)/s，总攻角为7°，将合角速度对应的俯仰、偏航轴角速度分为8种情况，总攻角对应的攻角和侧滑角分为8种情况，如表4所示。

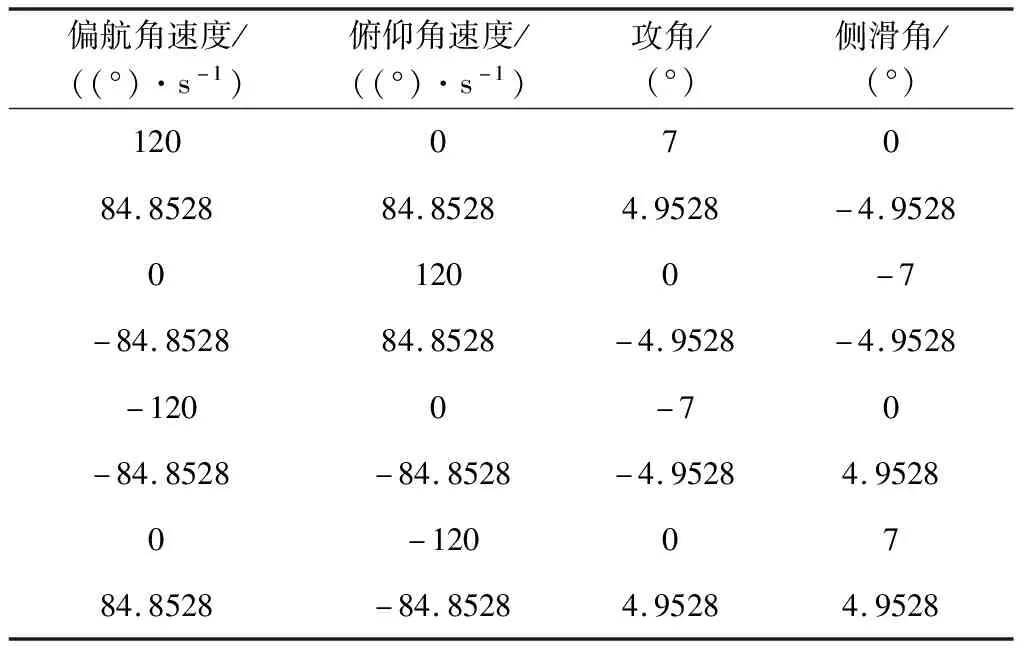
表4 分离相位(三维空间内摆动)

表4给出的攻角、侧滑角组合，对应了空间中8个姿态摆动平衡位置，代表不同的总伞绳力方向。偏航/俯仰角速度组合则包括了不同的摆动方向。在各平衡位置设置8种不同摆动方向，可获得覆盖三维空间各种摆动的64种情况。利用分析模型计算这64种情况对应的最近距离，其中最危险的分离相位为：偏航角速度为0(°)/s，俯仰角速度为120(°)/s，初始攻角为-7°，侧滑角为0°。

由此得出结论：防热大底分离最危险相位为背罩平台组合体在铅垂面内摆动，且分离时背罩平台组合体处于平衡攻角并向上旋转。

3.4 最危险分离相位原因分析

上述仿真结果表明，当背罩平台组合体在铅锤面内摆动，且分离时处于平衡攻角向上旋转时，防热大底分离发生碰撞的可能性最大。直观上，防热大底与背罩平台组合体均为轴对称外形，其气动参数也应具有对称特性，那么背罩平台组合体处于平衡攻角向下旋转时分离，最近距离大于最危险分离相位的原因需要进一步分析。

在最危险相位分离，防热大底初始攻角为-7°，分离后在惯性的作用下向上旋转，其攻角由负攻角变为0°再逐渐增大，在这一过程中，防热大底所受气动阻力相比分离瞬时逐渐增大，在0°后逐渐减小。而处于平衡攻角向下旋转时分离，防热大底攻角不断减小，所受气动阻力相比分离瞬时逐渐减小。因此最危险分离相位情况下，防热大底所受平均气动阻力大于向下旋转的情况，防热大底与背罩平台组合体质心距离也小于另外一种情况。

3.5 摆动峰值角速度与分离马赫数对安全性影响

在确定最危险分离相位的基础上，分析背罩平台组合体姿态摆动峰值角速度以及分离马赫数对安全性的影响。

分离时刻马赫数影响降落伞、背罩平台组合体及防热大底的气动参数，根据图2的仿真结果，当分离马赫数较大时，可能出现防热大底的气动减速度大于背罩平台组合体的现象。此时与摆动峰值角速度的影响叠加，使最近距离大幅减小。因此具体分析方法为给定摆动峰值角速度和不同分离时刻马赫数，利用分析模型仿真计算短期分离过程中最危险相位对应的最近距离，保守地确定安全分离峰值角速和马赫数范围。

设定摆动峰值角速度范围为60(°)/s至160(°)/s，利用分析模型每20(°)/s进行一组仿真，每组仿真考察分离马赫数分别为0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9和1.0时对应的最近距离，仿真结果如图15至图20所示。

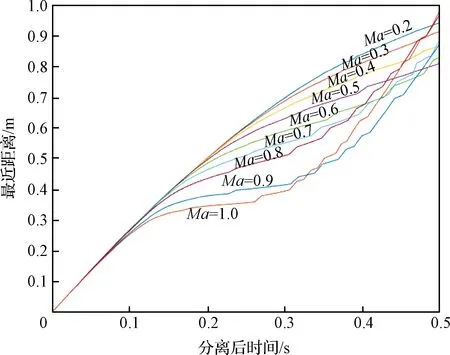
图15 不同马赫数对应的最近距离(峰值角速度60(°)/s)

图16 不同马赫数对应的最近距离(峰值角速度80(°)/s)

图17 不同马赫数对应的最近距离(峰值角速度100(°)/s)

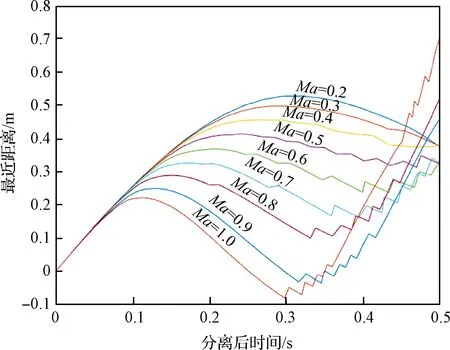
图18 不同马赫数对应的最近距离(峰值角速度120(°)/s)

图19 不同马赫数对应的最近距离(峰值角速度140(°)/s)

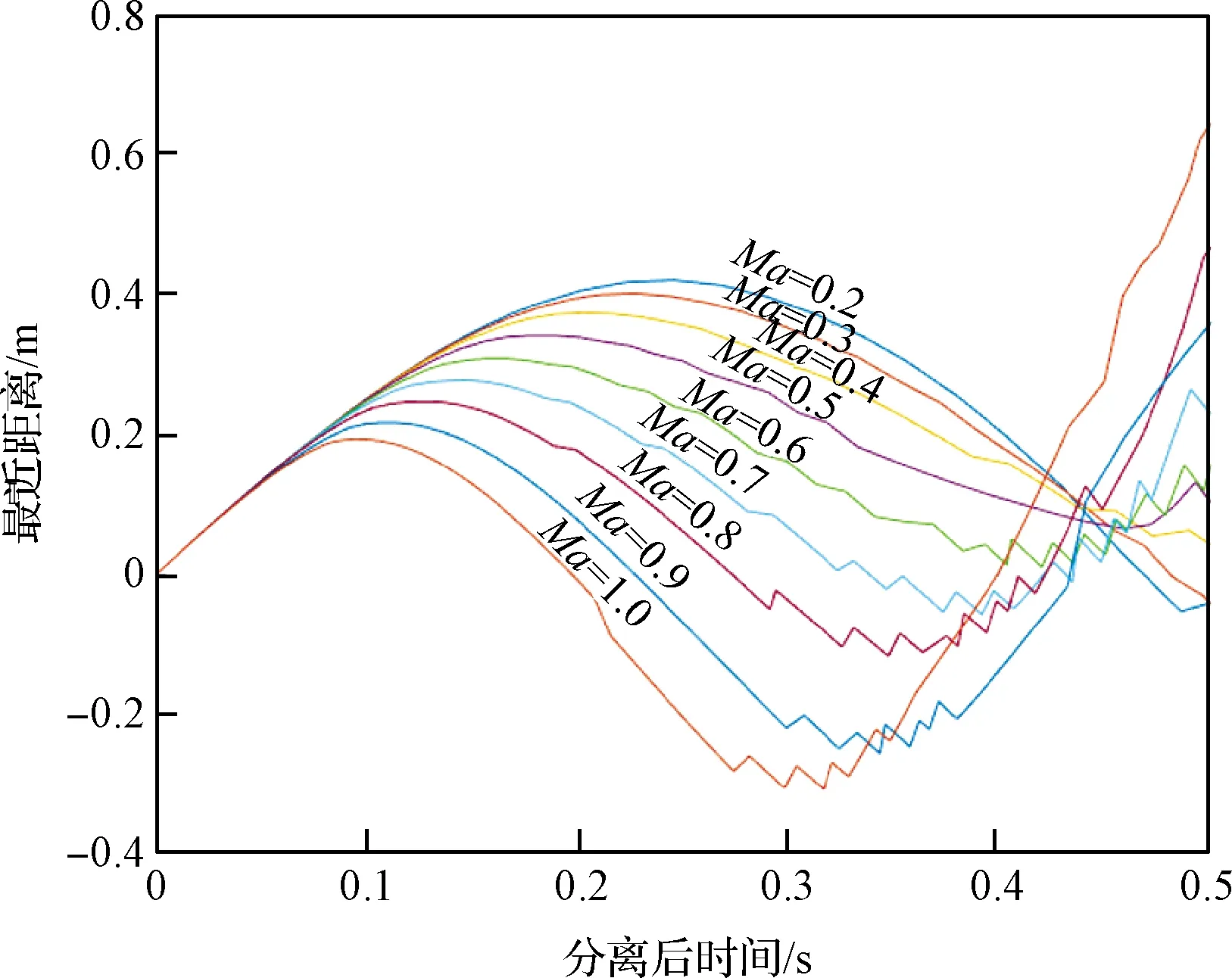
图20 不同马赫数对应的最近距离(峰值角速度160(°)/s)

由仿真结果可以得出：相同峰值角速度条件下，马赫数在0.2～1范围内，分离马赫数越大，防热大底与背罩平台组合体发生碰撞的可能性越大；同一分离马赫数条件下，峰值角速度越大，碰撞的可能性越大。

另外根据仿真结果，当分离马赫数为0.7时，峰值角速度小于140(°)/s可以保证防热大底脱离导轨后最近距离极值大于0 m，即安全分离。同样的，当分离马赫数分别为0.8、0.9和1.0时，峰值角速度需分别小于130(°)/s、110(°)/s和100(°)/s才能确保安全分离。将可以安全分离的马赫数和峰值角速度范围描绘出来，如图21所示，点划线区域为可安全分离的马赫数和峰值角速度区域。

4 防热大底安全分离条件

我们已经通过最危险分离相位给出了防热大底安全分离的马赫数与摆动峰值角速度范围，但摆动峰值角速度很难直接测量，无法直接用于分离触发判定。不过在伞降过程中，着陆器姿态摆动产生的原因主要是降落伞喘振，且随着喘振过程结束，降落伞伞绳力矩将逐渐消减摆动角速度，这使得摆动角速度峰值与着陆器马赫数存在一定的关联关系。这里将通过蒙特卡洛仿真给出着陆器峰值角速度与马赫数的统计关系，进而确定防热大底安全分离的马赫数范围。

利用降落伞和着陆器组合体六自由度动力学模型进行了2000次蒙特卡洛仿真，着陆器俯仰与偏航合角速度峰值外包络与马赫数关系如图21中实线所示。为了忽略部分极端峰值角速度的影响，我们计算每条合角速度曲线的外包络线，近似得到每条弹道对应的峰值角速度曲线，并在每个马赫数处统计2000个峰值角速度标准差，根据3法则将3处的峰值角速度作为该马赫数对应的最大峰值角速度，从而给出峰值角速度统计规律与马赫数关系。

图21 安全分离触发马赫数确定

着陆器姿态运动由于伞绳力矩作用主要为俯仰和偏航轴有较大角速度，而滚转角速度可以忽略。2000条弹道对应的角速度与马赫数关系说明在降落伞喘振结束后，着陆器角速度峰值随着马赫数的减小而逐渐减小。

结合安全分离峰值角速度范围，当最大峰值角速度降至安全范围内时，对应的着陆器马赫数则为防热大底安全分离马赫数。

5 结 论

本文针对中国火星探测任务“天问一号”防热大底分离过程进行了深入研究，通过分析脱离导轨后的防热大底与背罩平台组合体相对运动特性，揭示了降落伞伞绳力矩使着陆器产生的姿态摆动是尾流区回流作用之外又一个产生碰撞的主要原因。利用建立的相对姿态运动分析模型，定量地给出了分离时姿态摆动相位与最近距离的关系，确定了最易发生碰撞的危险分离相位，并基于该工况联合分析了分离马赫数、姿态摆动峰值角速度与分离安全性之间的关系，给出了可安全分离的马赫数-峰值角速度范围。最后，根据着陆器姿态摆动峰值角速度随马赫数降低而减小的规律，将峰值角速度限制转化为马赫数约束，给出了防热大底安全分离的触发条件。本文所给出的防热大底分离安全性影响因素分析方法同样也是完整的分离触发条件确定流程，可为我国后续的火星探测任务设计提供借鉴。