Comprehensive compensation method for the influence of disturbing gravity field on long-range rocket guidance computing

Yansheng WU, Zongqiang WANG, Bing ZHANG

a China Aerospace Science and Technology Corporation, Beijing 100048, China

b Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China

KEYWORDS Disturbing gravity field;Long-range rocket;Online compensation;Stellar guidance;Vertical deflection

Abstract With the improvement of the accuracy of the inertial system, the influence of the disturbing gravity field on the accuracy of long-range rocket has become increasingly prominent.However, in actual engineering, there are problems of low accuracy and being time-consuming for disturbing gravity field compensation. In view of this, this paper proposes a set of online comprehensive solutions combining disturbing gravity reconstruction and stellar correction. According to the pre-launch binding parameters, the net function assignment method is used in the navigation system to calculate disturbing gravity in the boost phase online. In the guidance system, a closed-loop guidance online compensation method is proposed based on the state-space perturbation method for the disturbing gravity in the coast phase. At the same time, the vertical deflection can also be corrected by stellar guidance. The calculation results are simulated and verified under different circumstances. Simulation results show that the proposed online compensation algorithm has an accuracy improvement compared with the element compensation algorithm on ground.And the stellar guidance algorithm can further correct the impact deviation. The impact deviation after comprehensive compensation does not exceed 50 m, and the compensation percentage is greater than 65%.

1. Introduction

The factors that affect the accuracy of the long-range rocket’s impact deviation mainly include the vertical deflection of the launch point and the disturbing gravity during flight. The latter can be divided into the boost phase disturbing gravity and the coast phase disturbing gravity.For a long-range rocket with a range of 10000 km, the impact deviation caused by the disturbing gravity field can reach the order of kilometers.In the case of maneuver launch,the influence of initial localization and orientation errors can also reach the order of kilometers.As we all know,with the improvement of inertial devices,the influence of tool error on the accuracy of the impact deviation has been significantly reduced. And the trust deviation and aerodynamic deviation will not cause the impact deviation when the guidance system is well designed. Thus, in order to improve the accuracy of the next generation of long-range rocket, it is necessary to compensate for the disturbing field.

According to the analysis of the existing data, the longrange rockets of the United States,Russia and other countries have compensated for the influence of the disturbing gravity field. The American ‘‘Trident” is the world’s most advanced submarine-launched long-range rocket. The impact deviation can reach 90 m with a maximum range of 11000 km.Russia’s ground-based mobile rocket, RT-2PM2, has a short preparation time for launch, and the impact deviation can reach 350 m when the range reaches 10500 km.The French submarine-launched rocket, the M51, which entered service in 2015, adopts the inertial-stellar guidance system. When the maximum range is 10000 m,the impact deviation can reach 200 m. Without the implementation of disturbing gravity field compensation, these accuracies are difficult to achieve.

Some scholars have also studied the impact and compensation of the disturbing gravity field. Without considering the earth’s rotation and oblateness, Gore analyzed the influence of initial localization and orientation errors based on a series of simplifications, and deduced the mapping relationship between the shutdown point state deviation and the vertical deviation.Jia improved this method by taking into account the influence of the earth’s rotation.However, the above methods only consider the influence of the geometric term of initial localization and orientation errors,but not the influence of the force term. Wang et al. studied the conversion relationship between the launch point’s geodetic coordinate system and the astronomical coordinate system, and analyzed the influence of initial localization and orientation errors on the force exerted during the flight, so as to improve the analysis accuracy of error propagation.Chatfield et al.and Hidebrant et al.analyzed the effect of imprecision of reference gravity model on inertial navigation performance. Wells et al. discussed the method of gravity gradiometer to improve inertial navigation.Ma et al.distinguished the influence mechanism of the vertical deflection on the standard trajectory and the actual flight trajectory. Besides, an analytical model about how the vertical deviation affects the navigation and required velocity calculation was derived. Zhao et al. adopted the cubic equidistant b-spline function approximation method and the finite element interpolation method to assign the disturbing gravity, thereby improving the accuracy of the disturbing gravity assignment.Zhou et al.deduced the mathematical relationship between the terminal position deviation and the various corrections, and compensated for the gliding trajectory affected by perturbation factors. Renanalyzed the influence of the disturbing gravity on the missile’s free flight phase trajectory.He not only constructed the perturbation equations of three methods of isometric, isocentric distance,and isochronous,but also derived the analytical solution of the state transition matrix of the perturbation equation,which provided a new way for the rapid analysis of the influence characteristics of the disturbing gravity in the free phase. On this basis, Zhengput forward the state space perturbation equation of free phase with equal height model.Xie et al.made a rapid evaluation of the disturbing gravity with the ‘‘funnel-shaped” finite element construction method of standard trajectory. Under the premise of ensuring accuracy, the single-point disturbing gravity assignment for the boost phase and the coast phase did not exceed 20 us. Wang et al.studied the influence of disturbing gravity in the boost phase and coast phase on the closed-loop guidance,and compensated the disturbing gravity of coast phase.

The above references mainly compensated for the influence of vertical deflection or disturbing gravity at the algorithm level. However, in the actual flight process of long-range rocket, it is comprehensively affected by both vertical deflection and disturbing gravity.In this paper,a complete compensation scheme is put forward for the practical engineering application. Combined with the configuration of the onboard control system, the disturbing gravity field is well compensated with the consideration of vertical deflection and disturbing gravity during flight.That is, the disturbing gravity of boost phase is calculated quickly with the net function assignment method in the navigation system. The initial state error and the disturbing gravity of coast phase are compensated in the guidance system. Aimed at the non-spherical gravity in the free phase, this paper proposes an on-line compensation method for long-range rocket closed-loop guidance considering the earth non-spherical gravity perturbation in the free phase based on the state space perturbation method. Simulations show that this scheme has the characteristics of short ground preparation time, high compensation accuracy and strong engineering practicability.

This paper is divided into seven parts. Following the introduction,the impact mechanism analysis of the disturbing gravity field on the long-range rocket is introduced in Section 2.Next, the comprehensive compensation idea is presented in Section 3.Section 4 and Section 5 describe the proposed compensation method in the navigation system and the guidance system respectively. Simulations and analysis are shown to prove the effectiveness of the proposed scheme in Section 6.Finally, the conclusion is presented in Section 7.

2.Impact mechanism analysis of disturbing gravity field on longrange rocket

2.1. Impact mechanism of initial state error

Initial state errors include the vertical deviation calculation error, the transmitting azimuth error, the geodetic longitude error, the geodetic latitude error, the geodetic elevation error,etc.They will lead to the reference error of coordinate system,the initial positioning error, the initial velocity error and the force error caused by initial state errors.Among them,the reference error of coordinate system is the most important,which can be characterized in the form of error angle, that is, the misalignment angle of the rocket reference platform.The misalignment angle of platform α is the error angle between the inertial platform system P and the launching inertial coordinate system I.Considering that α is a small quantity,the transformation matrix from P to I can be expressed as

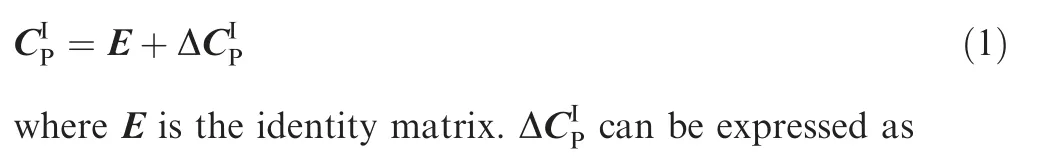
where Wis the apparent acceleration,which can be measured by the accelerometer.

At present, long-range rockets generally adopt closed-loop guidance scheme, and the navigation errors will directly affect the calculation of the required speed. Then the accuracy of impact deviation will be affected.It can be analyzed as follows.

After calculating the state errors at the shutdown point through Eq.(5),the impact deviation caused by the initial state error can be obtained according to the partial derivative of the impact deviation with respect to velocity and position:

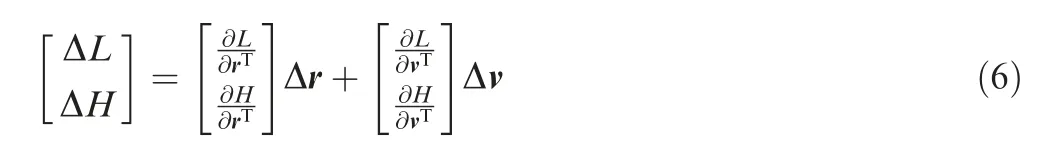
where ∂L/∂r, ∂H/∂r, ∂L/∂vand ∂L/∂vare the partial derivative of the impact deviation with respect to velocity and position at the shutdown point.

2.2. Impact mechanism of boost and coast phase disturbing gravity

The influence of boost phase disturbing gravity on the longrange rocket control system is mainly manifested in the calculation of the true velocity and position. The true velocity and position increment of the boost phase can be obtained from the following equation:

where F(v;ρ;t)is the expression of the required velocity when the coast phase disturbing gravity is taken into consideration,and F (v;ρ;t)is the expression of the required velocity when the coast phase disturbing gravity is not taken into consideration.Combined with Eq. (5), the impact deviation caused by the boost phase and coast phase disturbing gravity can be obtained.

3. Comprehensive compensation idea

According to the above analysis, the following compensation strategy is adopted to compensate the impact of the disturbing gravity field as much as possible. The impact of the boost phase disturbing gravity is compensated in the navigation system. For this reason, it is necessary to solve the problem of rapid calculation of the high-order disturbing gravity. And the impact of coast phase disturbing gravity and the initial state error is compensated in the guidance system. Among them, the former is compensated by the required speed, while the latter is compensated by the stellar guidance. The above compensation strategy is divided into two parts: Pre-launch work and on-line work.

3.1. Pre-launch work

For long-range rockets, the pre-launch preparations for disturbing gravity compensation mainly include:First,a standard trajectory without considering the disturbing gravity is determined according to the launch mission. Then, a flight pipeline based on the standard trajectory is constructed, and the flight pipeline is divided by the finite element method. Based on relevant measurement data of perturbed gravitation, the node coordinates disturbing gravity of the boost phase and coast phase are calculated by means of point mass or spherical harmonic function. Grid division diagrams of boost and coast phases are shown in Fig. 1.In the stellar correction section,the optical navigation star is calculated by simplex tuning method according to the rocket parameters, the standard trajectory, and the loaded ephemeris. On this basis, four optimal correction coefficients can be calculated.And the preparation for the stellar correction is completed.The specific process is shown in Fig. 2.

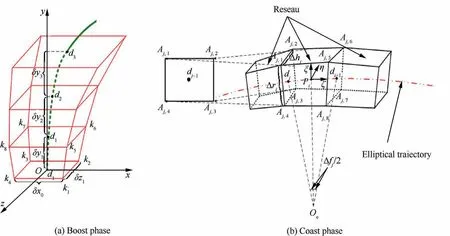
Fig. 1 Schematic diagram of space grid division for boost and coast phases.

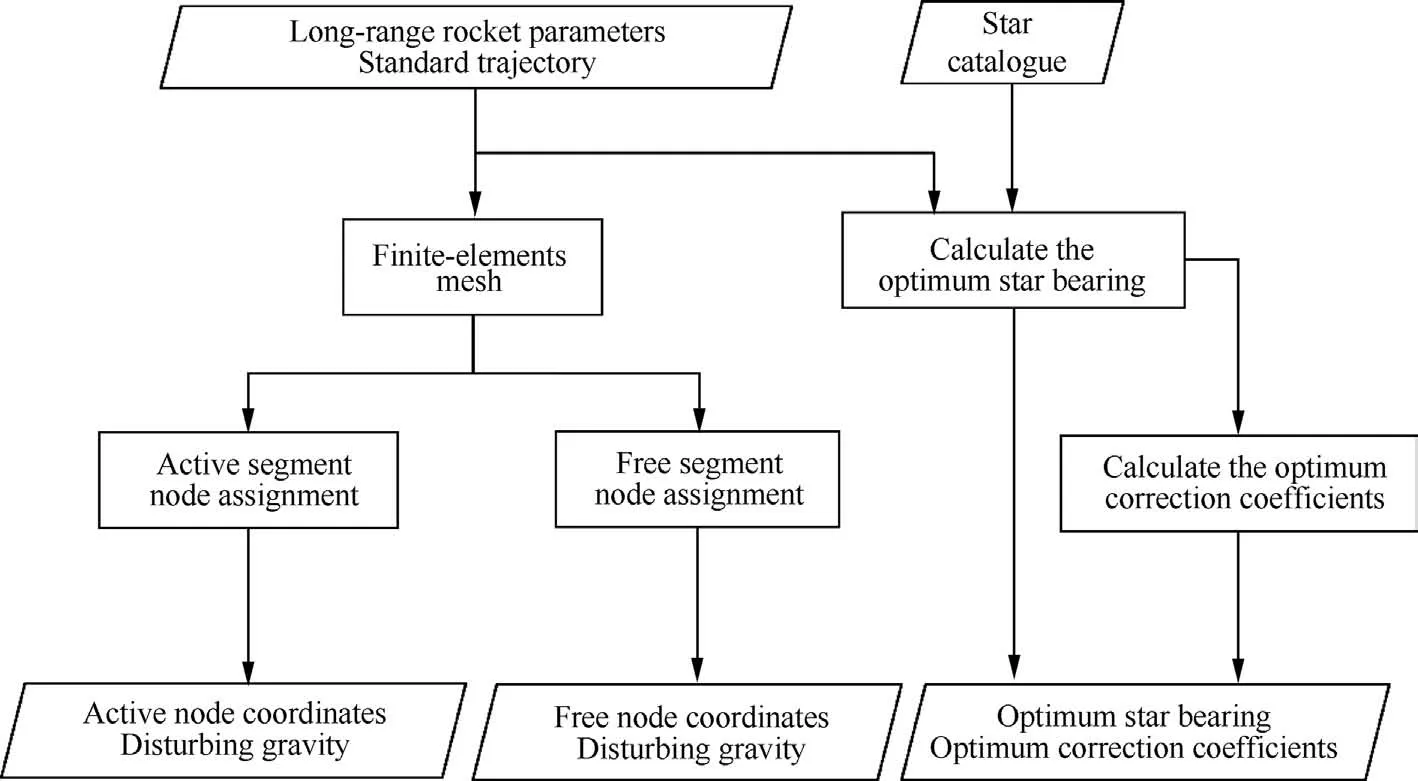
Fig. 2 Pre-launch flowchart of long-range rocket.

To sum up,in addition to the routine preparation of launch parameters, the following parameters need to be calculated and bounded as well:

(1) The elements required to compensate the boost phase disturbing gravity: boost phase node coordinates, node disturbing gravity.

(2) The elements required to compensate the coast phase disturbing gravity: free phase node coordinates, node disturbing gravity.

(3) The elements required to compensate the initial state error: Ephemeris, the optical navigation star and optimal correction coefficients.

3.2. Online work

Fig.3 shows the online workflow of the disturbing gravity field compensation. According to the required parameters of prelaunch bounded, true velocity, true position and guidance instructions can be obtained by compensating the impact of disturbing gravity field in the navigation and guidance system.In the navigation system, the unit where the rocket is located can be rapidly calculated based on the current position of the rocket. Therefore, the disturbing gravity acceleration of the current position can be calculated quickly and introduced into the navigation equation. Combined with the inertial navigation measurement, true velocity and position can be obtained. In the guidance system, the impact deviation caused by the free phase disturbing gravity is calculated based on the pre-launch bounded elements. And the required velocity correction is further calculated. In the final modification section,the total required velocity correction can be obtained by combining with the impact deviation caused by the estimated initial state error measurement. Finally, according to the guidance system without considering the impact of disturbing gravity,the guidance instruction is generated,and the impact deviation can be corrected.

Fig. 3 Online compensation flowchart of perturbed gravitation.

4. Navigation system compensation

The basic method of boost disturbing gravity compensation is to calculate the disturbing gravity acceleration quickly based on pre-launch bounded parameters and introduce them into navigation equations. Since the element subdivision and node assignment have been completed before launch, the work on the rocket is mainly to judge where the rocket is located, and calculate the disturbing gravity with the unit node value.

The disturbing gravity can be quickly calculated by the type function assignment method and the net function assignment method.Because the net function assignment method has high precision and is acceptable, this paper mainly introduces how to calculate the boost phase disturbing gravity with the net function assignment method.

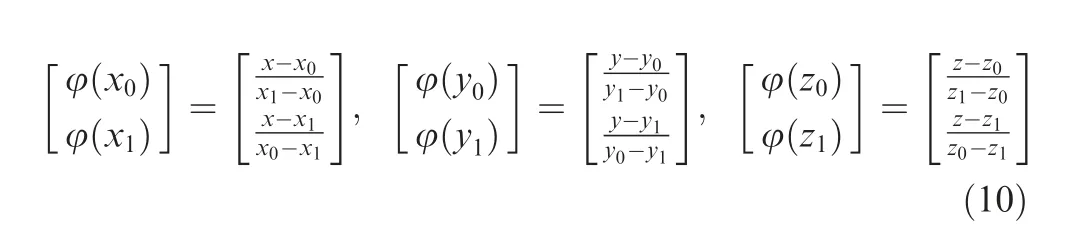
According to the net function approximation theory, the disturbing gravity at any point in the unit can be calculated as

Fig. 4 Network function cell diagram.

5. Guidance system compensation

The idea of the guidance system compensation adopts the reconfiguration model of the disturbing gravity to quickly predict the trajectory terminal deviation caused by the disturbing gravity at the final stage and convert it into the required velocity correction. Then before final repairing, adjust the attitude according to the bounded parameters, so that the star sensor is aligned with the optimal navigation star. Therefore, the azimuth and the elevation of the optimal navigation star can be measured through the star sensor, and the impact deviation caused by the initial state error can be further calculated.Combined with the impact deviation caused by the disturbing gravity in the free phase, the velocity correction amount is calculated. The impact deviation can be corrected in the final repair section.

5.1. Closed-loop guidance compensates for the free-phase nonsphere gravity online

Closed-loop guidance is one of the guidance methods for advanced spacecraft at present. The basic idea is a guidance method that uses the concept of required speed to associate the target position with its current position according to the target position and the current state. Closed-loop guidance can calculate the deviation to the required terminal conditions in real time, and form guidance instructions accordingly, which can control the missile in real time and eliminate the deviation to the terminal conditions.When the terminal deviation meets the guidance mission requirements, the command is issued to shut down the engine.The American ‘‘Apollo” spacecraft adopted the speed gain guidance method of closed-loop guidance.In order to overcome the influence of atmosphere and earth oblation in the reentry stage, many researchers have proposed a variety of closed-loop guidance methods in literatures, such as the predictive closed-loop guidance method based on Runge Kutta method,the ballistic iterative determination method based on the virtue target point,and the improved closed-loop guidance method based on impulse.Conventional rocket closed-loop guidance mainly compensates the perturbation factors such as the earth oblateness by strategy of calculating the virtual target point before launch, which is not good for the quick launch of rockets due to the long pre-launch preparation time. And the compensation effect is poor when the actual flight trajectory of the rocket is quite different from the standard trajectory. To solve the above problems, this paper proposes a closed-loop guidance online compensation method based on the state space perturbation method with considering the non-spherical gravitational perturbation of the free phase. The specific compensation process can be described as follows:

Step 1. In each guidance period, the required velocity vshould be calculated based on the two-body dynamics model. The core is to solve the problem of Lambert.

Step 2. Taking the real-time predicted shutdown point state and target point position on the projectile as input conditions, the rocket terminal state deviation ΔXcaused by the non-spherical gravity in the free phase can be calculated online with the analytic prediction model proposed in Refs.In order to ensure the calculation accuracy of ΔX, Ref.divided the free-phase non-sphere gravity into Jterm and the disturbing gravity term, and derived the corresponding analytical calculation model of ballistic error propagation respectively. The analytical calculation model of ΔXcan be obtained by linear superposition of the two:

Step 3. Calculate the gain velocity correction Δv. According to the error propagation perturbation equation in the free flight section of the trajectory, the following equation should be satisfied if the gain velocity correction amount can eliminate the position term and time term deviation in the rocket terminal deviation.

5.2. Starlight guidance compensates for initial state error

For submarine-launched or land-launched long-range range rockets, it is difficult to establish an accurate global vertical deviation model. And the alignment error is large. Therefore,the inertial-stellar guidance system can be adopted to compensate. In the inertial-stellar guidance system, the misalignment angle caused by the initial state error can be calibrated taking advantage of the directionality of star. The impact deviation can be corrected according to the misalignment angle, so as to improve the guidance accuracy of long-range rockets. The flow of stellar guidance to compensate for the initial state error can be described as follows:

Step 1. According to the selected navigation star and misalignment angle, the measurements can be calculated by

Step 3. Calculate the corrected gain velocity Δv. On the basis of calculating the stellar composite guidance impact deviation, the required velocity of the guidance point can be further calculated. Then the velocity correction Δvcan be obtained according to the actual velocity and required velocity. The corrected gain velocity Δv can be obtained by combining the gain velocity correction Δvof the coast phase disturbing gravity.

where Δv is the gain velocity before correction.

6. Simulation analysis

Fig. 5 show the influence of the disturbing gravity field in four regions and the comparison results of compensation. It can be seen from the figures that the influence of the disturbing gravity field on the long-range rocket is not only related to the launch position,but also related to the launch azimuth.More-over, both the method proposed in this paper and the element compensation algorithm can effectively compensate for the influence of the boost and coast phase disturbing gravity,and improve the accuracy of the long-range rocket. At the same time, it can be seen that the scheme proposed in this paper is more effective than the element compensation algorithm on ground in most cases.

Table 1 Launch sites with large difference in topography.

Fig. 5 Comparison of compensation results in 4 regions.

In order to better compare the proposed method in this paper with the element compensation algorithm on ground,Fig.6 show the comparison of the disturbing gravity compensation error percentages in four regions. And Table 2 shows the comparison results of the two methods when the shooting direction is 120°.

It can be seen from the figures that, in most cases, the method proposed in this paper can better correct the impact deviation caused by the disturbing gravity compared with the element compensation algorithm on ground, and the disturbing gravity compensation percentage is more than 10%.Even in a small number of cases, the compensation effect of the element compensation algorithm on ground is better and no more than 4%.And it can be seen from the figure that when the launch azimuth is 0°, the element compensation algorithm cannot effectively correct the impact deviation caused by the disturbing gravity. Then the scheme proposed in this paper is used to comprehensively compensate for the initial state error,the boost and the coast disturbing gravity. The compensation percentage of the disturbing gravity field in the four regions are shown in Fig. 7.

Fig. 6 Percentage comparison of disturbing gravity compensation in 4 regions.

Table 2 Compensation results of four regions when shooting direction is 120°.

It can be seen from the figures that the initial state errors also have a great impact on the impact deviation. After correcting the influence of the disturbing gravity, correcting the impact deviation caused by initial state errors can further increase the percentage of disturbing gravity compensation.

In order to reflect the computational efficiency of the proposed method in this paper, it is compared with the RKF(Runge-Kutta-Fehlberg) method. The calculation time under different disturbing gravity models is calculated respectively,and the results are shown in Table 3.

It can be seen from the table that the calculation time of RKF numerical method under different disturbing gravity models is different. Under the condition of the same calculation accuracy,the calculation time of 8*8-order model is about 0.0234 s. And the calculation time of 36*36-order, 72*72-order, and 108*108-order model is 0.376 s, 1.195 s and 3.663 s respectively. The calculation time of the proposed method in this paper is 0.0040 s, and the calculation time is independent of the order of the disturbing gravity model. At the same time, it can be seen that the higher order the disturbing gravity is, the more significant the relative calculation efficiency of the analytical solution is.

As an example of 120 degrees shooting, Table 4 shows the compensation results of four regional disturbing gravitation.It can be seen from the table that different launch positions have great influence on the impact deviation caused by disturbing gravity, but the impact deviation caused by the initial error has almost nothing to do with the launch position.By comparing the calculation results,it is found that the compensation percentages of the disturbing gravity field in the four regions are 91.11%,79.93%,92.22%and 91.17%respectively,which indicates that the scheme proposed in this paper can effectively compensate for the impact deviation caused by the disturbing gravity impact.

Fig. 7 Percentage comparison of disturbing gravity field compensation in 4 regions.

Table 3 Comparison of calculation time under different disturbing gravity models.

Table 4 Compensation results for four regions at 120 degrees.

7. Conclusions

In the compensation scheme for the influence of the disturbing gravity field on the accuracy of the long-range rocket,the influence mechanism of the disturbing gravity field is analyzed.Combined with pre-launch preparations and online work, a comprehensive compensation idea is determined. The navigation system is used to compensate for the boost phase disturbing gravity, while the guidance system is used to compensate for the coast phase disturbing gravity and the initial state error.Numerical simulations verify the necessity and feasibility of the scheme, and the results show that the scheme proposed in this paper can effectively compensate for the impact deviation caused by the initial state error, the boost phase and coast phase disturbing gravity.Therefore,the accuracy of long-range rocket can be improved.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This work was supported by National Basic Research Program of China (No. 613222)