实践中的生本四环课堂教学研究

孔令锋

【摘要】课堂教学改革不能只从理论上去研究，更要付诸于课堂实践中进行探索反思。任务驱动、问题引导式“生本四环”自主课堂又称“生本课堂”。生本课堂注重各层次学生的能力发展，以“学”为出发点，体现的理念是：把课堂还给学生，把学习时间交还学生，把发言权交还学生。重视“学的过程”要远远大于“学的结果”育人为上的一种课堂教学行为。

【关建词】小学数学;导学设计;先学后教

任务驱动、问题引导式“生本四环”自主课堂又称“生本课堂”。

课堂教学所体现的理念是：把课堂还给学生，把学习时间交还学生，把老师解放出来，“以生为本，以学为主;先学后教，兵教为主”的一种课堂模式。其特色是：先学后教，学是学生学，教是学生教。是以发展学生的学习能力为前提，重视“学的过程”要远远大于“学的结果”的一种育人为上的课堂教学。下面以《分数的简单应用》为例解读生本课堂的导学设计與课堂流程。

一、导学设计前的教材分析

分数的初步认识是在三年级上册第八单元开始学习，其要求是初步认识1/几/几，;会读写简单的分数，通过图示来比较简单分数的大小，能计算简单的同分母分数的加减。能解决有关分数的简单实际问题。感悟数形结合的数学思想、方法、发展数感，体会分数的应用与价值。

对于如何具体描述分数的意义和性质、单位“1”的理解，则是在五年级下册才开始学习。关于分数的乘除法学习则是在六年级上册的教学内容。

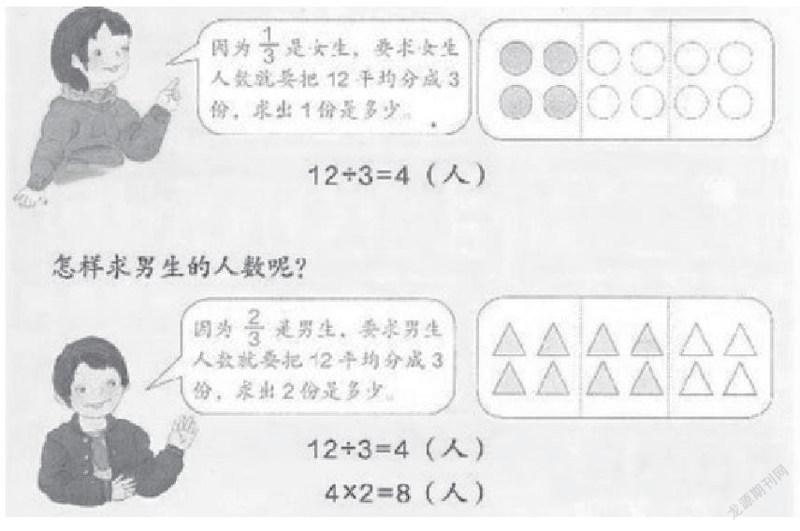
比如三年级《分数的应用》例2的数学信息：有12个学生，其中的1/3是女生。问：女生有多少人？实际就是高年级里的“求一个数的几分之几是多少”用乘法来解决的数学问题。

关于分数的应用，高年级常见的分率句有：女生人数是总人数的1/3;或女生人数占总人数的1/3......但在三年级分数的应用例2的教学中是以“有12个学生，其中的1/3是女生”来描述数学信息。编者的意图很明显是为了区分，避开了高年级的数学思维。三年级的学习是要学生理解：把12平均分成3份，每份是多少？“分母是几就平均分成几份”的平均分数学思维。而不是根据分数乘法的意义来计算“12的1/3是多少”的数学思维。

因此，该课的重点是通过数形结合让学生对分数有着进一步的理解。分数的应用是通过多元表征之间的转换来逐步加深对分数的认识。如：根据已知分数进行分一分、涂一涂、说一说的数形结合来加深理解分数的含义。例2由数到形是在例1由形到数基础上的一种思维转换。要启发学生的多角度思考，就要找准思考的切入点。该课的特点是：图形、语言、算式三种表征的结合，而且是要让学生在图形、语言、算式表征不断转化的过程中掌握解决这类问题的方法。因此，该课的切入点重在理解：把哪个数平均分？怎样平均分？为什么要这样分？这就要联系到例1。例1由形到数，也就是看图形平均分成几份，分母就是几;取几份，分子就是几。例2由数到形，就要反过来思考，看分母是几，就平均分成几份。看分子是几，就取几份。

二、导学案的作用与设计意图

综上对教材的理解，该课的导学设计是建立在“以学为主，兵教为主”的理念，培养学生自学自探的能力为前提来构思：问题引导，怎样才能起到精准导学的作用。

（一）导学案的学习目标是针对学生的课堂学习，要突出“我”主人翁的主体地位：

1.加深理解分数的含义，我能用平均分的方法来解决数学问题。

2.通过自主学习，合作交流，提高我的分析、判断、创编说理能力（语言表达、交流能力）。

重点：用平均分的方法来解决数学问题;难点预测是学生对图式结合的数理分析。体现在学生自主探究与合作交流中对于“几/几、图形、算式”相互转化的过程能否把思路说得清楚。这也是本课导学设计首要思考如何突破的问题。这个问题得到突破，那么该课的知识目标就得到达成。更体现了“自主学习，合作交流，提高我的分析、判断、创编说理能力”的情感、能力目标得到落实。

其次，思考①：例2为什么在描述“1/3是女生”时用   来独立作一个图解，在描述“2/3是男生”时又另用   一个图来独立分析？为什么不两图合一？我认为是为了更直观的帮助学生理解“平均分”“取几份”的归一问题。因此，重在理解“平均分”“取几份”“怎样算”，对学生的自学也降低了难度。附例2图：

思考②能不能通过两图合一理清“1/3是女生”“2/3是男生”？这是否会对于学生的学提高了难度？反复思考，我认为可取，把总数平均分成3份，明确了其中的1份是女生，那么另外的两份就是男生。这也是与前面课课例所学的由形到数的思维相符的。在“学”的设计上也各有优势，在导学案的独学设计中又更显得精简。而且也是有据可依。

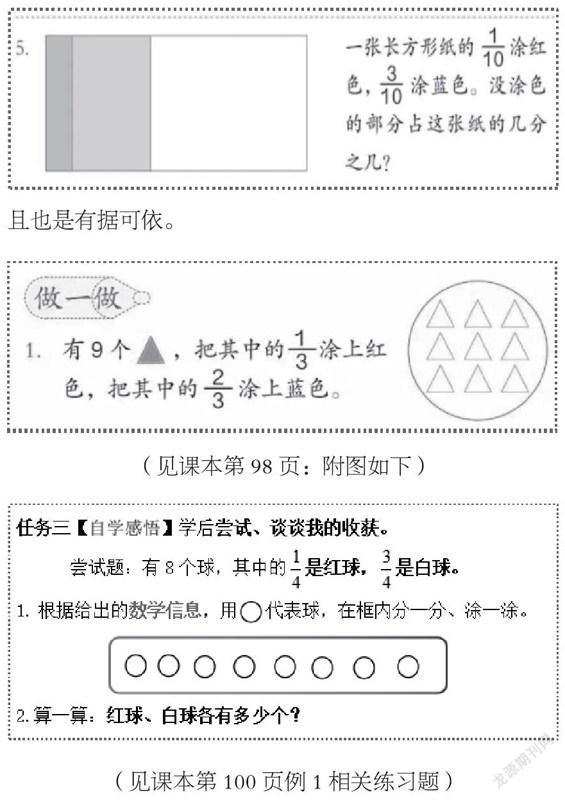
因此，在独学任务三尝试题的设计中本着“利用好教材，又不被教所利用，在操作上要实现化繁为简”的理念又大胆的把课例2的“两图析题”设计为“合一图解题”，同时又是为延学的创编埋下伏笔：（附下图：尝试题设计）

导学案的设计是否能够实现“精心编导”也与教者对教材的理解，以及如何挖掘编者的意图有关。对教材存在不同的理解，在导学设计上也存在较大的偏差。同时也要备学情，不同的班级，引入的设计，问题的设计，习题的设计都有差别。导学案设计总的意图在于“以生为本，以学为重”把课堂还给学生，把老师解放出来。追求“先学后教，教与学两者合一，学是学生学，教是学生教”的“兵教兵”学习环境。也就是说教与学都是发生在学生的身上。杜绝“讲授式”“填鸭式”。导学案的作用不是为做题而做题。导学案的使用不只是检查学生获取知识的效果，更是要凸显学生获知过程中的学习能力，语言表达能力，合作精神是否得到提升。

导学案的作用在于“引”与“导”，路还是得学生自己走才能有“跑得快”的脚力。在导学案的任务驱动，问题引导下，学生站老师的前面，教师则站在学生的背后看着学生跑。体现 的是“若不摔倒，绝不相扶的高度信任;如若摔倒也是先鼓励互助、自强”。

（二）导学设计的开放性

导学案的设计总体上显得比较开放。如《分数的应用》例2学案，独学任务一复习引入“我知道……”这是要体现学生收集数学信息的能力，也是语言表达能力的一种培养。又是为任务二的新课而埋伏笔。学生可以不写出来，但在合作学习中可以说：

我知道：把12个平均成3份……我知道：有2份没涂色。我知道......

（不同层次的学生获取不同的信息，问题的开放看似提高了难度，实则又是降低了难度，面向全体）

独学任务三谈谈我的收获：通常 是“我知道……我发现……我学会……”的句式。

是方法的归纳，是知识的整理，是学说一句完整的话，是语言表达能力的培养。该课的自学感悟，不同层次的学也有不同的学习体会，学生可以说：

我发现：  分母是几，就平均分成几份。 分子是几就取几份。 我能够：能用平均分的方法来解决数学问题。  我有疑问：为什么要平均分成3份……

老师在点评时，还是要引向方法的归纳，知识的整理：分母是几就把总数平均分成幾份，先求每份是多少。

延学环节的“百花竞放”是要发散学生的思维，是对获取新知的内化，更是要求对“语言表达能力的提升”作进一步的训练。同时又要照顾到各层次学生的学习能力。使其学科兴趣得到提高。在设计中也要预设到不同层次的学生会有不同的表现手法（如下图）：

不同的学生就有不同的分法，涂法，就会收集到不同的数学信息，也会有不同的数学问题：①红花多少朵？②白花多少朵？③红花、白花各 多少朵？④红花多还是白花多？⑤红花比白花多或少多少朵？……有的甚至一开始没有实现平均分，一份大，一份小，在历经“错”的分法后，才得以走回常规的思维“平均分”。那么我们就要启动一个“错”的功能。如下预计可能存在的学习现象：

4朵4朵的分，发现：不平均分。学生收集到的信息：1/5、4/5这些分数存在合理性吗？怎么办？原因在哪里？是学生对分法不撑握，还是对知识理解不透？

这种现象，我们要研究的是学生“学”的过程，“分”的过程，而不是“错”的结果。不能用一个错对的结果来评判学生的“学”。我们的设计不是为做题而做题。我们的设计是注重一个学的思维过程，兴趣的培养、能力的发展，创新的意识。

那么出现这样的现象，我们如何启动一个“错”的功能？借“错”而创新，拓展学生的思维。在此，我们首先要清楚我们的设计意图。这里的设计是创编数学题，是让学生运用所学的知识根据自己的能力来创出一道颇具合理性的数学题。目的是让学生在通过图形、语言、算式表征不断转化的过程中掌握解决这类问题的方法。从而实现巩固知识、反思提升，更是要促进语言表达能力，说理能力的提升。如何启动“错”的功能？

做法①“先补后割”的数学思维。让“错”的分法存在合理性，可行性，并进行深度思维的拓展，可谓一举多得。如下：（补2朵）

补2朵发现：平均分了，总数18朵变成了20朵，但得出的信息：其中的1/5是红花，可以求出 红花朵数了，

进入一个深度的思维，还可以求原来白花朵数。

深度的思维在哪里？思维的拓展在哪里？

“先补后割”的数学思维一目了然。

做法②当学生发现“不平均”时，擦掉分割线，重新分。这是一个修正的办法，但是这样不清楚，也或是擦不掉了。学生用的笔不是铅笔。怎么办？还是补，补害线。如下：

启动“错”的功能，撬动学生的思维，这就是一种机智。老师不可轻易就否定学生的劳动成果，重在鼓励为主，引其纠正。在展评时，既肯定学生的创编思维，又要回归课的重点。引导学生判断信息与问题的合理性。提高创编能力，说理能力。错与对，要体现的是学生是否参与了学习的过程，这里要凸显的就是学生个性的张扬，这才实现“百花竞放”的设计理念。

如果是为做题而做题，在传统的教学模式思维中是：老师讲新课，学生做练习，如果有学生做错了;这时老师再讲一次，学生再练一次.....表现上是老师讲了很多次，甚至老师讲的比学生做的时间更多---满堂灌。可就是塞不进学生的大脑。又或者是当堂做对了，可两天后再做却又是云里雾里。如此循环，优生倦了，学困生还是得不到帮助。优生、学困生对于老师的讲授无动于衷了。尽管老师恨不得把课堂时间平均分一节课下来，只能感叹“悲哀”。

因此，在课堂教学中注重一个学的过程远比注重一个做题错对的结果更为重要。

三、展示功能与课堂流程

导学案不必每题必展，导学案要展示的是核心问题，课的重点，学生的成果。如该课只建议展示尝试题与创编题。通过尝试题的展示来触及任务一、任务二的信息采集，新课例的三个问题要点;通过尝试题的展示来反映学生自学课例的能力，通过点评来突破重难点，并归纳方法、要点。通过创编题的展示来巩固知识，提升能力。生本四环环环相扣，生本课堂，又课课相通。每一课注重能力的提升，学法的形成，又都是在为下一课服务。

生本四环总的来说是一个“由静而动，再由动而静”环环相扣的学习过程。

独学环节从任务一到任务三是引导学生先走进课本，再走出课本。是培养学生阅读文本、收集信息、处理信息的自学能力。独学是一个“静”的学习场面。需体现出静而不闲。

互学环节一个兵教兵“动”的学习场面，要有“动而不乱”“善于沟通”“乐于沟通”的真学习。特别是在自由学，跨组学的时候，一定要做到“动而不乱”才能起到“乐中有学，学中有获”的效果;才能真正发挥小老师应有的功能;才能使能力目标，情感目标得到落实;又能最大限度的把老师从课堂中解放出来。

共学环节是体现成果展示、聚焦问题、互相赏析，又相互质疑，据理力争、敢于辩驳、达成共识的群学阶段。共学阶段，学生要聆听，教师也要静听。想说就说，是让学生先说，鼓励学生据理辩驳;对于一些问题，当生生之间，争议无果或是全班都没有异议时，都没有发现，没有达到点子上时;或是说，经过学生的展示、交流、争辩都没有实现“自主突破要点、难点”时。老师才加入点评，提出简单问题，追加深度问题。也就是说在问题之中追加问题。目的是要把学生引到点子上来讨论问题。而不是老师单方面过多的开展“师讲生听”的“填鸭式”“池灌式”“镶入式”的学习场面。

互学与共学既体现学生的合作能力，交流能力，又体现老师课堂上的驾控能力，教学机智。老师是听众又是学习的参与者;同时也是一个带着欣赏眼光的裁判。教师的语言要惜字千金，言之有果。切忌在同一个问题上重重复复的唠叨，要舍得放，就要点到即止。尽量做到把更多的时间交还学生。

延学环节是查漏补缺，也是思维巩固，通过1、2题的牛刀小试，检测达标、再进入到信息的处理，加工，创作成果，反思升华。这里就不单单是知识层面上的思维发展，更是注重不同层次的学生学法上，能力上的巩固提升，兴趣的培养。

课堂教学改革不能只从理论上去研究，更要付诸于课堂实践中进行探索反思。生本课堂总体上基于一个原则：把课堂交给学生，把时间还给学生，“放”是为了让学生跑得更快！

参考文献：

[1]蔡遥炘，冯荣雄，周存逃.乐从镇课堂教学改革规范与指南[M].佛山新城.