地裂缝场地隧道暗挖地表沉降影响因素分析

曹原， 黄强兵,2*， 康孝森,2， 苟玉轩， 王庆兵

(1.长安大学地质工程与测绘学院， 西安 710054； 2.西部矿产资源与地质工程教育部重点实验室， 西安 710054； 3.北京市政路桥集团股份有限公司， 北京 100045)

随着中国城市化进程的不断加快，城市规模不断扩大，人口也迅速增长，面临巨大的交通压力，发展大容量的公共交通是缓解城市压力，解决人地矛盾的有效措施[1]。西安市作为中国四大古都之一，是“一带一路”的核心区，由于近年来人口增长，地铁建设列入了西安城市可持续快速发展的重要任务。西安市地处汾渭盆地，地质条件复杂，过去超采地下水导致城区先后出现了14条地裂缝，而规划地铁线路几乎不可避免穿越地裂缝[2-3]，这些地裂缝的存在及发展，严重制约西安地铁建设，也成为西安市轨道交通的“心病”。

为了确保地铁隧道穿越地裂缝场地的安全性，目前已建和在建的线路基本均采用浅埋暗(明)挖法施工，结构上采用分段设缝加柔性连接、扩大断面等特殊措施来应对地裂缝对地铁工程的影响[3-4]，但该方法与措施在施工中产生较大扰动，对周边环境影响大，加之地裂缝场地地层破碎，在场地附近建(构)筑物密集的情况下暗挖施工对邻近建(构)筑物威胁较大，可能导致建(构)筑物变形与开裂破坏，从而造成不可预计的损失。

关于地铁隧道施工引起地表沉降的问题，中国学者已经开展了大量研究并取得了许多成果，如刘洪洲等[5]采用有限元法分析了盾构推进中地面沉降影响因素的影响规律；孙钧等[6]研究了盾构推进中交叠隧道土层地表沉降曲面的发展变化；郑淑芬[7]研究了盾尾注浆、上层覆土条件、双线隧道和掘进压力的不同开挖顺序等对地表沉降的影响规律；李小青等[8]分析了盾构隧道引起的位移场、应力场变化，讨论了不同的土体本构模型、不同的地层损失、土体排水和不排水条件下盾构施工引起的地表沉降规律；刘金慧等[9]研究了地层损失率和地表沉降槽宽度的变化规律，并给出了修正系数的范围；王昊统等[10]模拟了硬岩地区隧道的施工过程，并通过室内试验验证了五步开挖下隧道施工与地表沉降的关系；韩昌瑞等[11]采用数值模拟分析了隧道埋深、地层情况以及不同间距对地表沉降的影响；代维达[12]基于地表沉降监测数据分析，研究了开挖面积、车站埋深等对地表沉降的影响；韩煊等[13]基于沉降观测数据，讨论了Peck公式在不同地区的适用性，并给出了相关计算参数的建议值；徐明祥等[14]研究了地裂缝场地暗挖隧道施工影响范围等，上述研究基本集中在地铁隧道施工沉降的预测、施工过程的影响及沉降控制技术等方面，而地裂缝场地的地铁隧道施工地表沉降及其影响因素的研究鲜有报道。

因此，现针对地裂缝场地地铁隧道暗挖施工引起的地表沉降问题，以西安地铁6号线穿越f8地裂缝场地为工程背景，建立不同开挖施工方向(包括从地裂缝上盘至下盘、下盘至上盘)、不同隧道埋深、不同隧道洞径及穿越地裂缝角度4个不同因素影响下地铁隧道-地裂缝-地层地质力学模型，通过多工况有限元数值模拟计算，分析上述4个因素对地铁隧道穿越地裂缝场地暗挖施工地表沉降规律的影响，并给出地裂缝场地地铁隧道暗挖施工的影响因素优先顺序，以期为西安地裂缝场地地铁隧道暗挖施工及地表沉降控制提供科学依据。

1 工程背景

西安地铁6号线总长约39.94 km。一期工程线路起于西安市高新区南客站，止于劳动南路，全长约20.52 km(图1)。该线路穿越的地貌类型从西向东依次为皂河冲洪积平原，黄土梁、洼，浐灞河冲洪积平原(图2)，且沿线地形中间高，两边低，地表高度为405.9～426.8 m，地形总体平坦。线路穿越f8地裂缝场地位于丈八四路～丈八一路区间的锦业路，该段呈东西走向，区间全长1.08 km，其中f8地裂缝走向约北偏东43°，倾向南偏东45°，倾角约80°，与地面线路夹角约47°(图1)。该区间隧道穿越的f8地裂缝地层为：杂填土、黄土状土、粉质黏土、粉质黏土、粉质黏土、中砂、粉质黏土(图1)，隧道围岩综合分级为VI级[15]。隧道断面设计开挖跨度为9 m，高为9.2 m，埋深约9.5 m，如图3所示。该f8地裂缝场地采用传统的浅埋暗挖交叉中隔墙(cross diaphragm, CRD)工法，是一种应用于软弱地层、湿陷性黄土地层及地裂缝破碎带等不良地质条件下的城市地下工程建设工法。该工法是把隧道断面分开为4个开挖面(图1)，独立开挖支护，及时布设临时支护和初期支护，封闭成环；待隧道结构及周围岩土体变形稳定后拆除临时支护，随后进行隧道二衬施工。CRD工法各个导洞独立封闭成环，减小了隧道施工对周围岩土体的扰动，保障了隧道围岩的稳定性和施工过程的安全性。

图1 地铁6号线及研究区域情况Fig.1 The condition of Metro Line 6 and research area

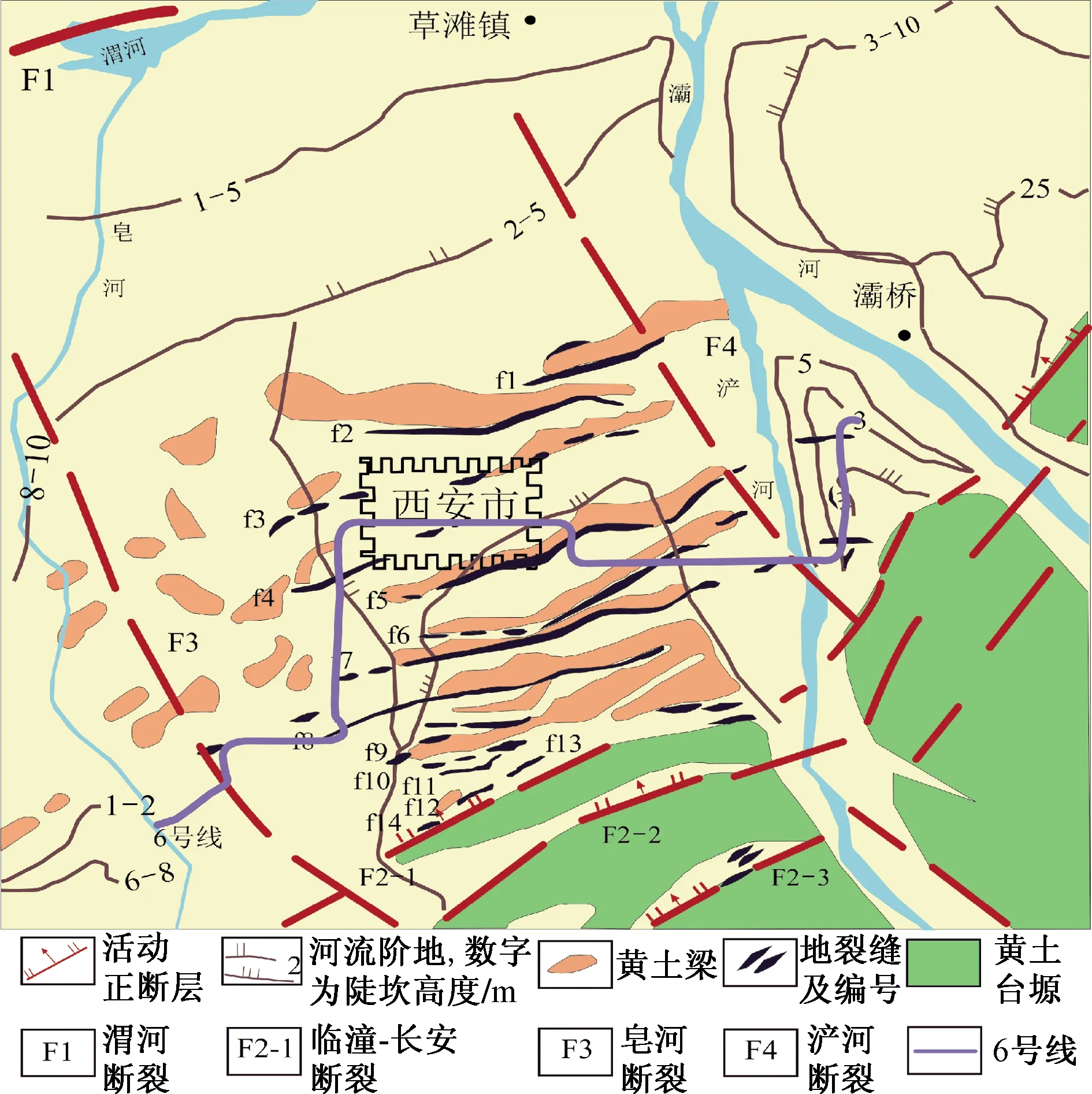
图2 地铁6号线沿线地貌Fig.2 Landform along Xi’an metro line 6

图3 隧道断面Fig.3 Tunnel section

2 有限元模型的建立和参数的选取

选取丈八四路～丈八一路右线K21+851.412～K21+996.412区间隧道穿越f8地裂缝为研究对象。采用Midas GTS NX软件模拟隧道施工穿越地裂缝的情况，数值模拟中各地层材料参数如表1[14-15]所示。地裂缝采用interface接触面模拟[16-17]，地裂缝参数如表2所示。

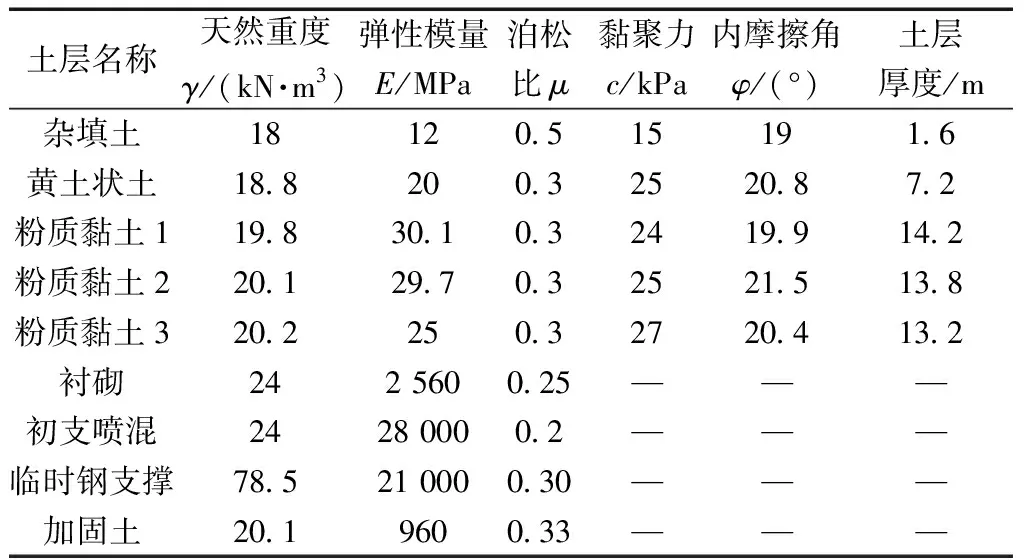
表1 模型材料参数Table 1 Model material parameters

表2 地裂缝参数Table 2 Ground crack parameters

地铁隧道暗挖施工穿越地裂缝带计算模型如图4所示，模型尺寸：长×宽×高=135 m×70 m×50 m，隧道埋深9.5 m，断面为马蹄型，地裂缝倾角为80°，与地铁隧道走向夹角为47°，初始应力场仅包含土体自重应力，不考虑附加荷载作用；围岩采用3D实体单元，简化为均匀连续介质，采用Mohr-Coulomb理想弹塑性本构模型；隧道结构中的临时钢支撑、初期支护均采用2D板单元模拟，设置固定参数属性，用弹性本构模型。边界条件为：x方向和y方向施加水平约束，模型底部施加z方向的垂直约束，模型顶部为自由面。

施工过程的计算结合前述的暗挖隧道施工工法进行了合理有效的简化，导洞开挖时先进行超前注浆加固地层，之后进行1导洞—2导洞—3导洞—4导洞开挖，如图5所示，当1导洞封闭成环5 m后，开挖2导洞，当2导洞封闭成环10 m后，开挖3导洞，当3导洞封闭成环5 m后即当开挖至如图5(右)所示各导洞位置时各导洞开始同步向前开挖(每一施工步为5 m)，这一施工过程可在分析中逐步激活导洞的相应区域实现。

图4 隧道暗挖施工穿越地裂缝带计算模型Fig.4 Calculation model of crack tape in tunnel dark excavation construction

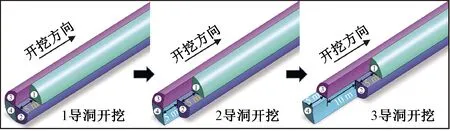
图5 暗挖施工过程Fig.5 Construction process of tunnel excavation

3 计算结果及分析

地裂缝场地CRD工法施工时，隧道开挖方向(包括从地裂缝上盘至下盘、下盘至上盘)、埋深、洞径及与地裂缝相交角度4种因素均对地表沉降有影响。考虑实际施工方案，分别以不同开挖方向、不同埋深、不同洞径以及不同斜交角度穿越地裂缝为单一分析变量进行11组工况的模拟(表3)，分析4种因素影响下的地表沉降规律。

3.1 不同开挖方向施工对地表沉降的影响

为分析隧道施工以不同方向穿越地裂缝过程中的地表沉降规律，在地表横向布设5条测线监测地表横向沉降量，即分别在开挖进尺15、40、65、90、115 m位置设测线J1、J2、J3、J4、J5(图6)。选取测线与隧道正上方地表中轴线相交点布设5个监测点，其中D0位于地裂缝处，S1与S2、X1与X2分别位于地裂缝上、下盘距地裂缝带25、50 m处。

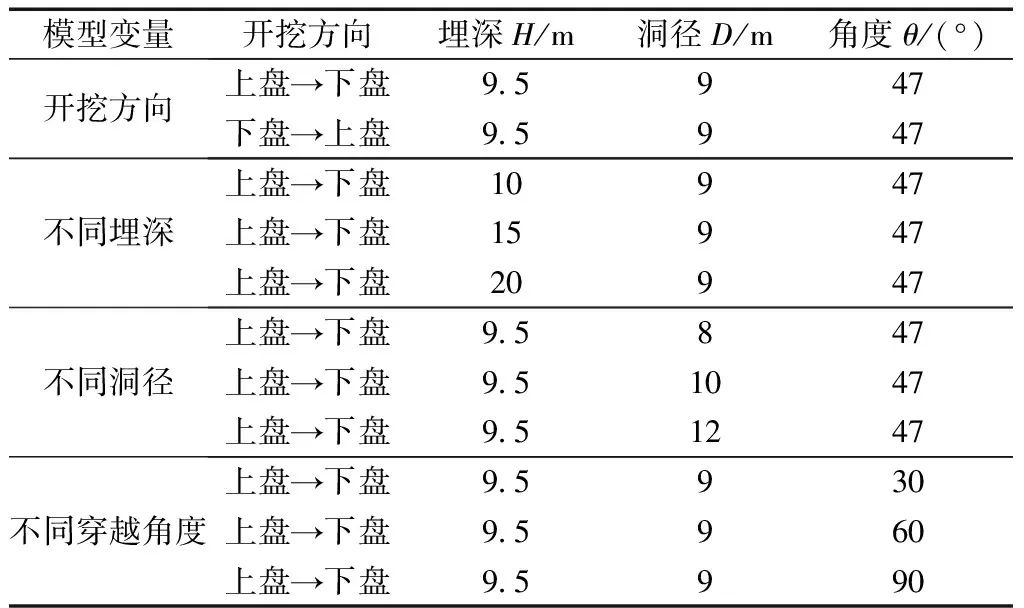
表3 模拟计算工况Table 3 Simulation calculation

图6 地表测点布设图Fig.6 Place of surface measuring point

3.1.1 地表沉降变化规律(纵向)

图7 不同开挖方向施工时地表监测点沉降变化曲线Fig.7 Surface monitoring point settlement change curve during different excavation directions construction

从上盘至下盘和从下盘至上盘两种不同开挖方向工况下隧道正上方地表监测点的沉降曲线如图7所示。由图7可知，隧道正上方地表沉降变化随开挖进尺呈反S形，其变形大致分为三个阶段：刚开挖时小变形、开挖中急剧变形以及开挖后平稳变形。隧道施工开挖时，隧道正上方监测点离开挖掌子面越近，受影响程度越大，沉降量越大，上盘监测点(S2、S1)沉降稍大于下盘(X1、X2)，地裂缝处地表监测点(D0)沉降最大。判断地裂缝场地隧道施工对上盘的扰动强于下盘，地裂缝处受扰动最强，易诱发地表破裂。

由两种不同开挖方向施工地表最终沉降对比曲线(图8)可知，开挖方向无论是从上盘至下盘施工还是从下盘至上盘施工，施工引起的地表最终沉降变化规律基本一致：沉降曲线均呈凹槽型，距地裂缝越近，地表沉降量越大；从上盘至下盘、下盘至上盘施工最大地表沉降量分别为33.96、33.86 mm，对于地表沉降控制而言，从地裂缝下盘至上盘方向施工略优于上盘至下盘。

图8 两种不同开挖方向施工地表最终沉降对比Fig.8 Two different excavation directions under construction surface final settling comparison

3.1.2 地表沉降影响范围(横向)

两种不同开挖方向下测线J3处横向地表沉降变化曲线如图9所示(不同位置的沉降曲线相差不大，因此仅给出地裂缝处沉降曲线)，横向地表沉降曲线呈凹槽型，隧道中轴线处地表沉降量最大，距隧道中轴线越远，地表沉降量越小。从影响范围来看，两种工况基本一致，说明两种开挖方向下地表沉降横向影响范围接近。地表沉降拟合曲线(R2=0.99)如图10所示。

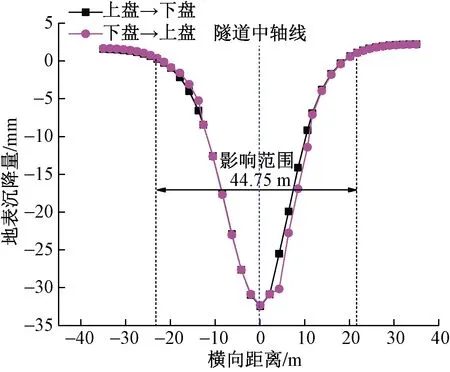
图9 测线J3横向地表沉降曲线Fig.9 Lands in the lateral surface settlement curve at J3

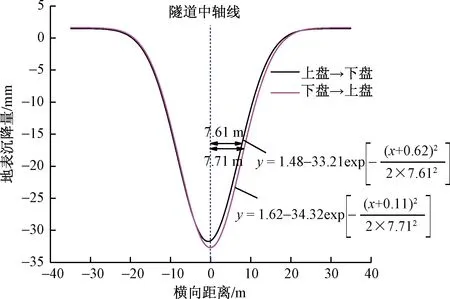
图10 地表沉降拟合曲线Fig.10 Surface settling fitting curve

3.2 隧道不同埋深施工对地表沉降的影响

3.2.1 地表沉降变化规律(纵向)

3种埋深(H=10、15、20 m)工况下地表监测点(图6)随开挖进尺变化的沉降曲线如图11所示。沉降规律与不同开挖方向一致，隧道正上方地表监测点沉降曲线呈反S形，地裂缝场地地铁隧道暗挖施工对上盘的扰动强于下盘，地裂缝处受扰动最强。

隧道中轴线地表最终沉降曲线如图12所示，3种工况下地表最终沉降变化规律基本一致，整体曲线呈凹槽型，地表最终沉降最大值均出现在地裂缝上盘，上盘地表最终沉降量大于下盘。隧道埋深为H=10、15、20 m时暗挖施工最大地表沉降量分别为34.83、38.87、42.35 mm，表明浅埋暗挖隧道穿越地裂缝带施工时地表沉降随隧道埋深的增大而增大，与韩昌瑞等[11]所得结论一致，即在地铁隧道埋深不超过30 m时，地表沉降量与埋深呈正相关。

图11 不同埋深(H)施工地表监测点沉降曲线Fig.11 Surface monitoring point settlement curve under different buried depth (H) construction

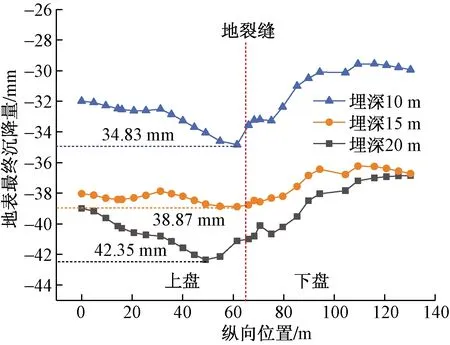
图12 不同埋深(H)施工地表最终沉降曲线Fig.12 Final settlement curve under different buried depth (H) construction

3.2.2 地表沉降影响范围(横向)

浅埋暗挖隧道以不同埋深(10、15、20 m)工况下测线J3处横向地表沉降曲线如图13所示，埋深对地表沉降的影响规律与不同开挖方向对地表沉降的影响规律相似，且此地表沉降曲线可以通过拟合曲线(R2=0.99)反映(图14)。从影响范围来看，地铁隧道埋深越深，地表沉降横向影响范围越大，表明地表沉降横向影响范围与地铁隧道埋深呈反比关系。

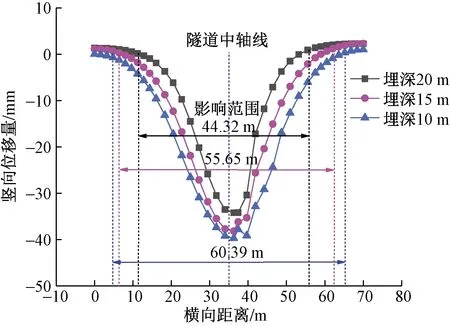
图13 测线J3横向地表沉降曲线Fig.13 Lands in the lateral surface settlement curve at J3

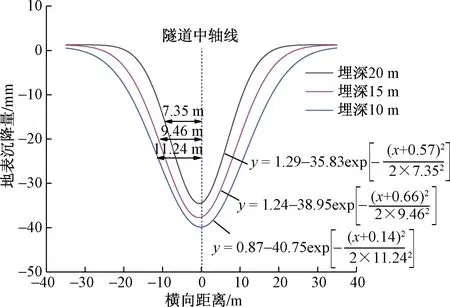
图14 地表沉降拟合曲线Fig.14 Surface settling fitting curve

3.3 不同洞径隧道施工对地表沉降的影响

3.3.1 地表沉降变化规律(纵向)

隧道3种不同洞径(D=8、10、12 m)工况下地表监测点(图6)随开挖进尺变化的沉降曲线如图15所示。总体变化规律与不同开挖方向、埋深条件基本一致，隧道正上方地表监测点沉降曲线呈反S形，地裂缝场地地铁隧道暗挖施工对上盘产生的扰动强于下盘，地裂缝处受扰动最强。

隧道3种不同洞径工况下隧道中轴线地表最终沉降曲线如图16所示，曲线整体规律基本一致，均呈凹槽型，隧道洞径为D=8、10、12 m施工时最大地表沉降量分别为36.85、61.89、102.89 mm，表明地裂缝场地地铁隧道穿越地裂缝带的洞径越小，所引起的地表沉降量越小。

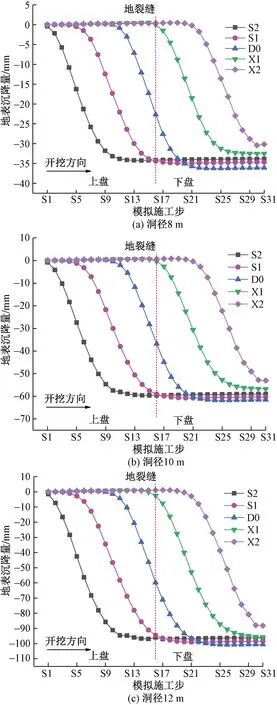
图15 不同洞径(D)施工地表监测点沉降变化曲线Fig.15 Surface monitoring point settlement change curve under different caviar (D) construction

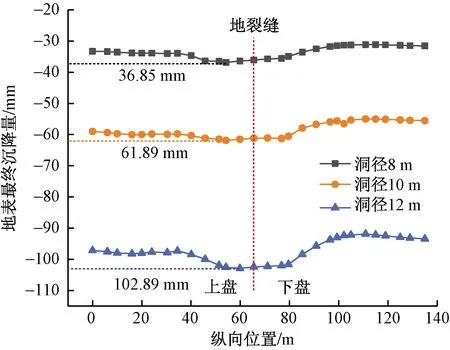
图16 不同洞径(D)施工地表最终沉降曲线Fig.16 Final settlement curve under different cavity (D) construction

3.3.2 地表沉降影响范围(横向)

浅埋暗挖隧道在3种不同洞径(8、10、12 m)工况下测线J3处(图6)横向地表沉降曲线如图17所示，由图17可知曲线规律与不同开挖方向的相似(图16与图8)，且此地表沉降曲线可以通过拟合曲线(R2=0.99)反映(图18)。从影响范围来看，隧道洞径越大地表沉降横向影响范围越大，表明地表沉降横向影响范围与隧道洞径呈正比例关系。

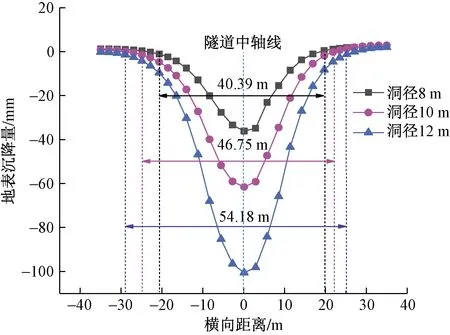
图17 测线J3横向地表沉降曲线Fig.17 Lands in the lateral surface settlement curve at J3

图18 地表沉降拟合曲线Fig.18 Surface settling fitting curve

3.4 不同角度穿越施工对地表沉降的影响

为了分析隧道不同角度(θ=30°、60°和90°)穿越地裂缝带时施工对地表沉降的影响规律，有限元模型尺寸为：长×宽×高=180 m×60 m×40 m。于隧道中轴线正上方地表布设监测点8个，即地裂缝处点D0，上盘分别距地裂缝20、40、60、80 m处的点S1、S2、S3、S4，下盘分别距地裂缝20、40、60 m处的点X1、X2、X3。除此之外，于地表横向布设5条测线，即分别在开挖进尺30、60、90、120、150 m处设测线J1、J2、J3、J4、J5，如图19所示。

3.4.1 地表沉降变化规律(纵向)

浅埋暗挖隧道以3种不同角度穿越地裂缝时地表监测点沉降随开挖进尺的变化曲线如图20所示，当地铁隧道正交和大角度斜交穿越地裂缝施工时，地表沉降变化规律基本一致，距地裂缝越近，地表监测点沉降量越大，且地裂缝上盘监测点沉降大于下盘，地裂缝处地表沉降量最大。由图20(c)可知当θ=30°(小角度斜交)施工时，地裂缝处地表监测点沉降量反而略小于上、下盘近地裂缝处的地表监测点，位移最大值出现在地裂缝上盘。表明正交或斜交穿越地裂缝带施工时对上盘的扰动强于下盘，且地裂缝处受扰动最强。

浅埋暗挖隧道以3种角度穿越地裂缝工况下隧道中轴线地表最终沉降曲线如图21所示，隧道中轴线地表最终沉降曲线整体规律基本一致，曲线呈凹槽型，最大沉降均出现在地裂缝上盘，且穿越角度为θ=30°、60°和90°时施工引起地表最大沉降量分别为51.88、33.26、28.23 mm，表明地铁隧道穿越地裂缝带的角度越小，引起的地表沉降量越大。

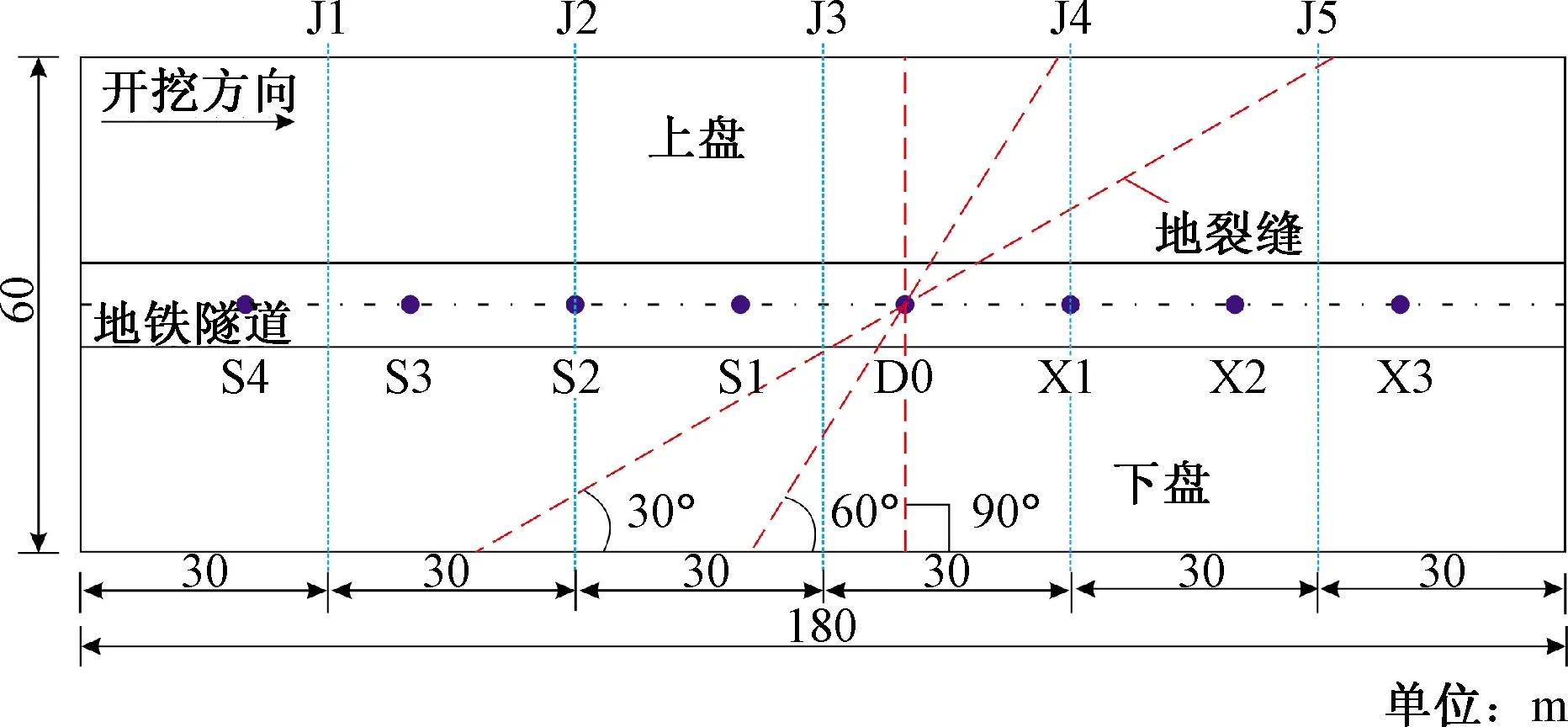
图19 地表测点布设图Fig.19 Place of surface measuring point

图20 不同穿越角度(θ)施工地表监测点沉降变化曲线Fig.20 Curve of surface monitoring point settlement changes under different crossing angles (θ)

图21 不同穿越角度(θ)施工地表最终沉降曲线Fig.21 Final settlement curve under different crossover angle (θ) construction

仅从中轴线地表最终沉降上看，隧道埋深、洞径与穿越地裂缝角度三个影响因素相较而言，地裂缝处均出现了差异沉降，且上盘沉降量均大于下盘，但不同洞径隧道穿越地裂缝的沉降变化较平缓。

3.4.2 地表沉降影响范围(横向)

浅埋暗挖隧道以3种角度(30°、60°、90°)穿越地裂缝时横向地表沉降曲线如图22所示，由图22可知此地表沉降规律与不同开挖方向的相似(图22与图9)，地表沉降曲线可以通过拟合曲线(R2=0.99)反映(图23)，不同工况下的地表横向影响范围相同，表明地表横向影响范围基本不受穿越地裂缝角度的影响。

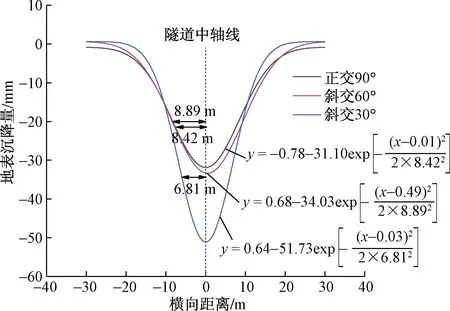
图23 地表沉降拟合曲线Fig.23 Surface settling fitting curve

4 工程中对各因素选择优先性讨论

以往研究表明地铁线路应尽量避开地裂缝地段，或者尽量与地裂缝正交或者大角度斜交穿越，避免小角度相交[2]，因此在浅埋暗挖施工过程中应首先考虑穿越地裂缝角度问题。另外，根据3.1节的计算结果表明，开挖方向对地铁隧道暗挖施工穿越地裂缝的地面沉降影响较小(图8)。而洞径和埋深对暗挖施工地表沉降影响程度的比较还需进一步讨论。因此选用正交试验设计进行二者的对比分析，开展2因子3水平的正交试验，分别以极差分析和方差分析来确定洞径与埋深的影响程度和显著性，以此对比各因子水平的改变对地表沉降的影响程度。

4.1 正交试验方案设计

以洞径D，埋深H作为正交试验设计的2个因子，洞径取8、10、12 m三个水平，埋深取10、15、20 m三个水平。选用L9(34)正交表进行方案设计和结果统计[18]，正交方案设计如表4所示。

表4 正交试验方案Table 4 Orthogonal test plan

4.2 计算结果与分析

为了更好地反映地裂缝场地地表沉降特点，取地裂缝中心测线J3(图6)横向地表沉降曲线，利用Gaussian函数进行拟合[13-14]，得到沉降量值y与距隧道中轴线横向距离x的指数函数关系式。

拟合公式为

(1)

式(1)中：A、C为曲线修正项；B为地表最大沉降量；Q为地表沉降槽宽度系数(取值如图10、图14、图18和图23所示)，即沉降曲线弯点到曲线对称中心的距离，反映了地表沉降的横向影响范围。计算结果如表5所示。

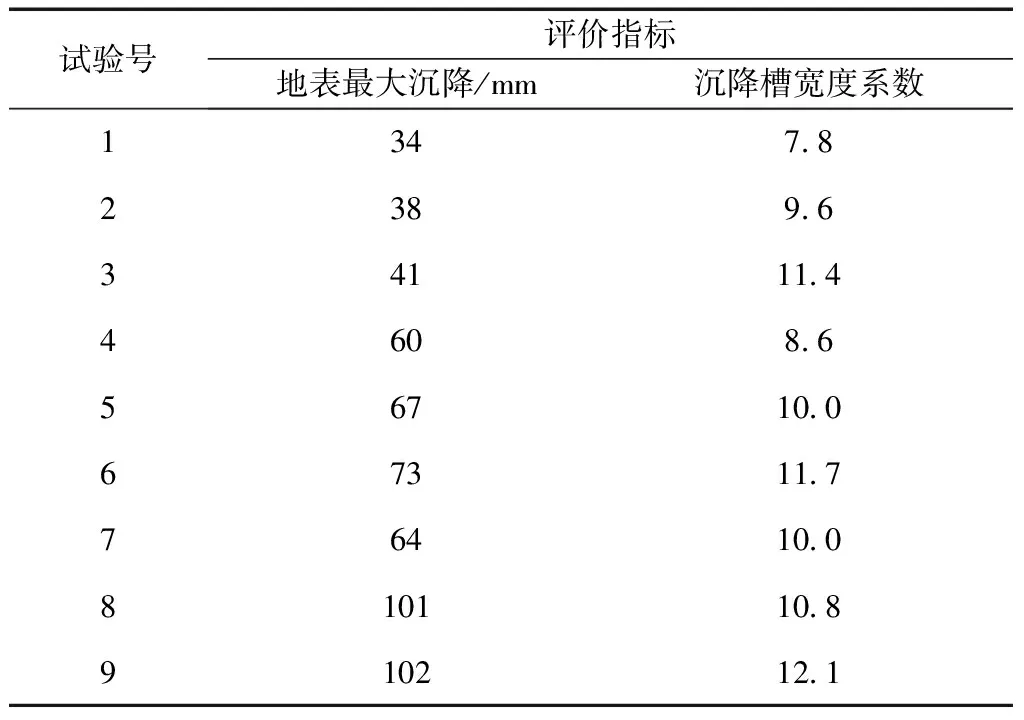
表5 数值计算结果Table 5 Numerical calculation results

4.2.1 影响因子极差分析

极差的大小反映了各因子水平改变对实验结果的影响程度[19]。地裂缝处地表最大沉降影响因子极差分析如表6所示。由表6可知，洞径和埋深的极差均大于误差项的极差，说明本次地表最大沉降正交试验设计是合理的。在此次正交试验设计中，由各因子水平变化梯度条件下极差的大小可知，在地裂缝场地上对地表最大沉降的影响程度：洞径D>埋深H。

沉降槽宽度系数影响因子极差分析如表6所示。由表6可知，洞径和埋深的极差均大于误差项的极差，说明本次正交试验设计是合理的。在此次正交试验设计中，由各因子水平变化梯度条件下极差的大小可知，在地裂缝场地上对沉降槽宽度系数的影响程度：埋深H>洞径D。

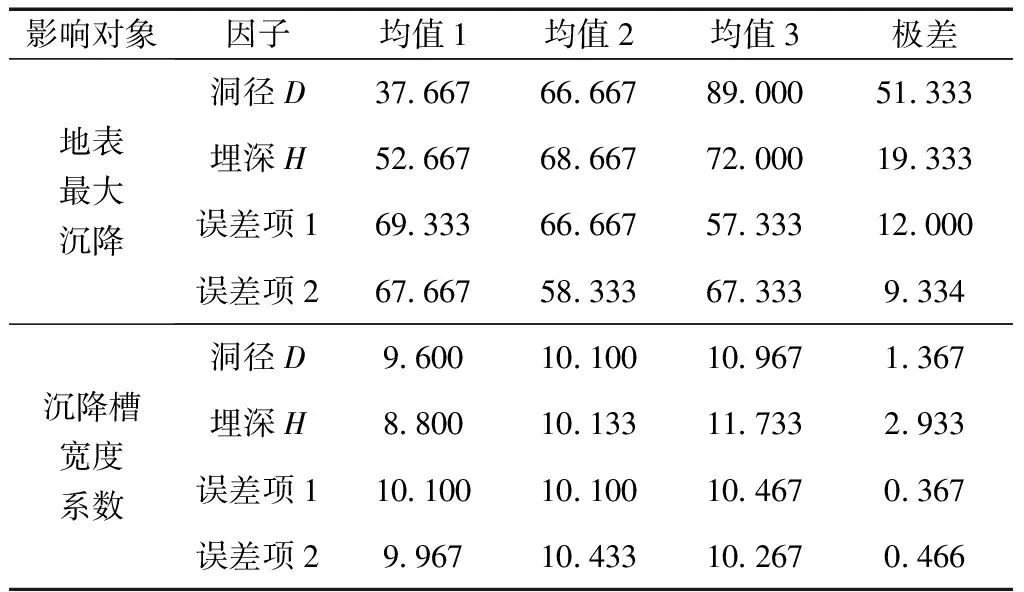
表6 影响因子极差分析Table 6 Pathorological analysis of influencing factors

4.2.2 影响因子方差分析

方差分析可以确定各因子对试验结果影响的显著性[19]。地表最大沉降影响因子方差分析如表7所示，由表7可知，在99%置信度(F临界值=6.940)下，地裂缝场地上对沉降槽宽度系数影响的显著程度为：洞径D较显著，埋深H不显著。

沉降槽宽度系数影响因子方差分析结果显示，与地裂缝处地表最大沉降相比，洞径和埋深发生改变时，沉降槽宽度系数均有不同幅度的变化，各因子均有显著性，且埋深H>洞径D。

表7 影响因子方差分析Table 7 Analysis of variance of influencing factors

综上所述，由于沉降槽宽度系数对各设计因子水平的改变较地裂缝处地表最大沉降敏感，因此以沉降槽宽度系数作为评价指标，建议在工程施工中对埋深的优先级应考虑排在洞径之前。

5 结论

以西安地铁6号线区间隧道暗挖段施工穿越地裂缝场地为工程背景，采用有限元数值模拟方法开展了不同开挖方向、不同埋深、不同洞径以及不同穿越角度等因素对地裂缝场地施工地表沉降的影响规律研究，并设计正交试验讨论了各因素的优先级，得出以下主要结论。

(1)不同开挖方向(上盘至下盘、下盘至上盘)施工引起隧道中轴线地表最终沉降曲线规律基本一致，地表横向影响范围不受其影响，但地裂缝场地地铁隧道从下盘至上盘施工更有利于控制地表沉降。

(2)地铁隧道浅埋暗挖穿越地裂缝场地引起的地表沉降量与隧道穿越地裂缝的角度呈负相关，与隧道埋深和洞径呈正相关。

(3)地裂缝场地地铁隧道浅埋暗挖施工地表沉降横向影响范围基本不受穿越角度的影响，但随埋深和洞径的增大而增大。

(4)基于正交试验设计的数值模拟，分析认为穿越角度对施工地表沉降影响最大，洞径、埋深次之，开挖方向影响最小。为了有效控制地表沉降，建议地裂缝场地地铁隧道暗挖施工方案优先采取顺序为：大穿越角度→浅埋深→小洞径→下盘至上盘开挖。