基于离散元的顺倾节理岩质边坡破坏过程分析

张水华，张 艳，梁栋才

(1.云南交投公路建设第三工程有限公司，云南 昆明 650103；2.云南省交通投资建设集团有限公司昆明东管理处，云南 昆明 650000;3.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，湖北 武汉 430071；4.中国科学院大学，北京 100049)

天然岩体由岩块和结构面组成，具有不连续性、非均质性和各向异性等性质。岩块的性质一般较为稳定，强度高，完整性好，不易变形，而结构面的力学性质较复杂[1]。结构面是岩体内部具有一定方向、规模和形态的连续或非连续面，如节理、裂隙和断层等[2-3]，其力学性质和分布状态直接影响着岩体的整体稳定性。

大量的工程实践经验表明，含有节理的岩质边坡发生破坏时，结构面往往起到主导作用。破坏沿结构面逐渐不断发育，最终贯通成滑面，导致岩质边坡发生整体滑动[4]。因此，准确获取结构面的力学参数对岩质边坡工程的设计和防护有重要意义。

对于岩质边坡的研究﹐一般是通过物理试验和数值模拟多种手段相结合的方式进行。物理试验结果真实准确，但存在不可重复、成本高等弊端；数值模拟具有高效率、低成本和可重复等优点，并且可对模型内部参数进行实时监测。颗粒离散元方法能够从细观尺度模拟岩石颗粒的摩擦特性和黏结特性，能模拟岩土体的几何及力学特性，可以直观地模拟岩体中裂纹的萌生、扩展和贯通过程。

目前，利用颗粒流离散元数值模拟结合物理试验对结构面性质的研究取得了一定的进展。在物理试验方面，Homand等[5]对花岗岩人工结构面循环加载，拟合出结构面循环剪切强度经验公式。Lee等[6]建立考虑结构面表面粗糙度的结构面剪切本构模型。Jafari等[7]和瞿佳美[8]使用水泥砂浆研究了剪应力和法向应力应变的变化特征。夏才初等[9]明确了随着法向应力的增大，结构面峰值抗剪强度增大。刘博等[10]等详细分析了结构面的变形破坏特征以及峰值剪切强度的劣化效应，拟合出了结构面循环剪切强度计算公式。由于物理试验监测手段有限，尤其是对结构面内部的监测不充分，大部分物理试验不能反映内部变形特征。在数值模拟方面，常文斌等[11]、Liu等[12]、Yoon[13]、何春梅[14]、黄达等[15]、王刚等[16]以及刘新荣等[17-18]、王雅婷等[19]、郑泽松等[20]通过考虑不同的法向压力、接触面粗糙度、边界条件等因素，使用PFC离散元法获得了岩体结构面细观损伤演化全过程及典型破坏模式。

上述内容为利用PFC2D软件研究含结构面岩质边坡破坏特征提供了强有力的借鉴。研究区露天矿边坡西南区域出现较大范围垮塌。根据地质调查结果，该区域边坡主要由灰岩组成，并发育有顺倾节理。本文采用颗粒流离散元软件PFC2D对边坡破坏过程进行模拟仿真，基于工程实地采集的灰岩样本和结构面样本的强度试验结果对离散元模型细观参数进行标定，监测边坡数值模型内部的位移、速度、裂隙发育和力链的发展过程，研究了顺倾节理对岩质边坡失稳破坏过程、破坏模式影响。

1 离散元模型细观参数

试验是确定岩体力学参数最基本的手段和方法。对于边坡工程，可通过室内试验，取得符合实际的岩体力学参数，再通过标定等手段将力学参数赋予数值模拟模型中，可直接检测到岩土体内部参数的动态变化，实现多角度岩土力学问题研究。在离散元模型研究中，细观参数选择的合理性直接影响到模拟结果的真实性。通常在选定离散元颗粒基本模型后，采用“试错法”反复试算标定模型细观参数。本节使用单轴压缩试验确定边坡主要岩层灰岩的细观参数，通过室内结构面剪切试验确定边坡体顺倾节理面的细观参数。

1.1 灰岩细观参数选取

根据某矿露天边坡的实际情况，选取有代表性的矿岩进行物理力学参数的试验测定。单轴压缩试验采用数字控制的电液伺服试验机RMT-150C岩石力学试验系统。试验时，采用力-位移的加压方式，以0.002 mm/s的速度均匀加荷，直到试样破坏。试验过程中试样加载前后对比如图1所示。

图1 试样加载前后对比图

依据《工程岩体试验方法标准》[21](GB/T 50266—2013)中相关规定采用下式计算岩石抗压强度：

(1)

式中：R为岩石抗压强度，MPa；P为最大破坏荷载，N；A为垂直于加荷方向的试样面积，mm2。

采用离散元软件建立单轴压缩试验模型时，颗粒间的接触选取平节理模型。平节理模型通过将接触模拟成由许多子接触组成的平线(2D)或圆盘(3D)来克服平行黏结模型的缺陷，在颗粒间接触破坏后，阻碍其旋转，能得到较为符合实际的压拉比。在软件中生成长10 cm宽5 cm的岩石样本，长度方向在岩石两个端面上以恒定速度0.002 mm/s来实现加载，借助软件中的FISH语言记录应力和应变。采用“试错法”最终得到数值模拟模型参数如表1所示。

表1 灰岩数值模型参数

数值模拟与室内试验破坏模式对比如图2所示，主要呈现为拉伸破坏与室内试验结果吻合。数值模拟试验的应力-应变曲线如图3所示，峰值大小与室内试验接近，由于天然岩石内部分布有一定的劣化面，因此峰值出现时间略早。总体而言，变形破坏趋势基本吻合，抗压强度的试验值83.16 MPa和模拟值80.48 MPa接近，误差小于4%。

图2 数值模拟与室内试验破坏模式对比

图3 单轴压缩应力-应变曲线

1.2 结构面细观参数选取

某露天矿边坡中，灰岩缓向反倾，但边坡普遍存在一组顺坡向结构面，对台阶及局部边坡稳定性起到控制作用。为此，在研究区对顺倾结构面取样，进行室内结构面剪切试验。根据《工程岩体试验方法标准》[21](GB/T 50266—2013)和《岩土工程勘察规范》[22](GB 50021—2001)、《非煤露天矿边坡工程技术规范》[23](GB 51016—2014)等规定，本次岩石结构面剪切试验进行五级法向应力的剪切试验，分别是500 kPa、1 000 kPa、1 500 kPa、2 000 kPa、2 500 kPa，剪应力分5级—10级施加，记录峰值剪应力作为结构面破坏强度。试验过程法向应力采用伺服控制，试样及试验情况，如图4、图5所示。

图4 结构面剪切试样

图5 结构面剪切试验

各法向荷载下，作用于剪切面上的法向应力和剪应力应分别按下列公式计算：

(2)

(3)

式中：σ为作用于剪切面上的法向应力，MPa；τ为作用于剪切面上的剪应力，MPa；P为作用于剪切面上的法向荷载，N；Q为作用于剪切面上的剪切荷载，N；A为有效剪切面面积，mm2。

使用离散元软件中的光滑接触模型模拟结构面，试验数值模型和破坏后数值模型如图6、图7所示。二维结构面剪切试验数值试块由三部分组成，分别是上部试块，下部试块和结构面，试块整体尺寸为30 cm×30 cm，采用单轴压缩数值模拟试验标定的细观参数，结构面处采用光滑节理模型，具体参数如表2所示。法向应力分别设置为500 kPa、1 000 kPa、1 500 kPa、2 000 kPa、2 500 kPa，并伺服控制，剪切速度为0.05 mm/s。通过FISH函数记录剪切力大小并转化为剪应力。

表2 结构面数值模型参数

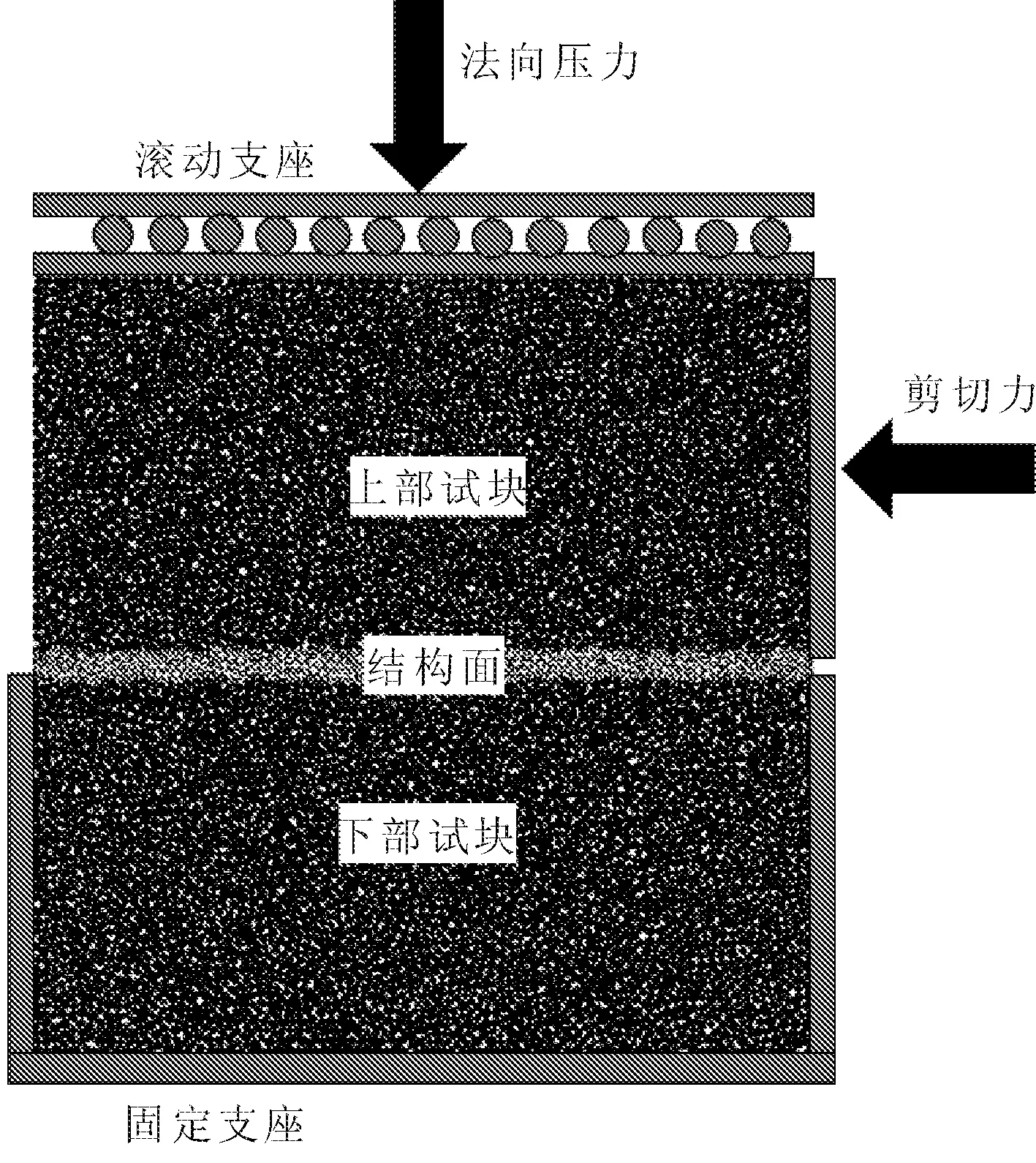
图6 结构面剪切模拟试验模型图

图7 结构面剪切模拟试验终止图

数值模拟试验和室内试验剪应力和法向应力关系如图8所示，绘制剪应力与法向应力关系曲线，并按库仑表达式确定相应的岩石强度参数(φ，c)见表3。数值模拟和室内试验得到内摩擦角和黏聚力接近，采用平滑接触模型模拟结构面具有可行性。

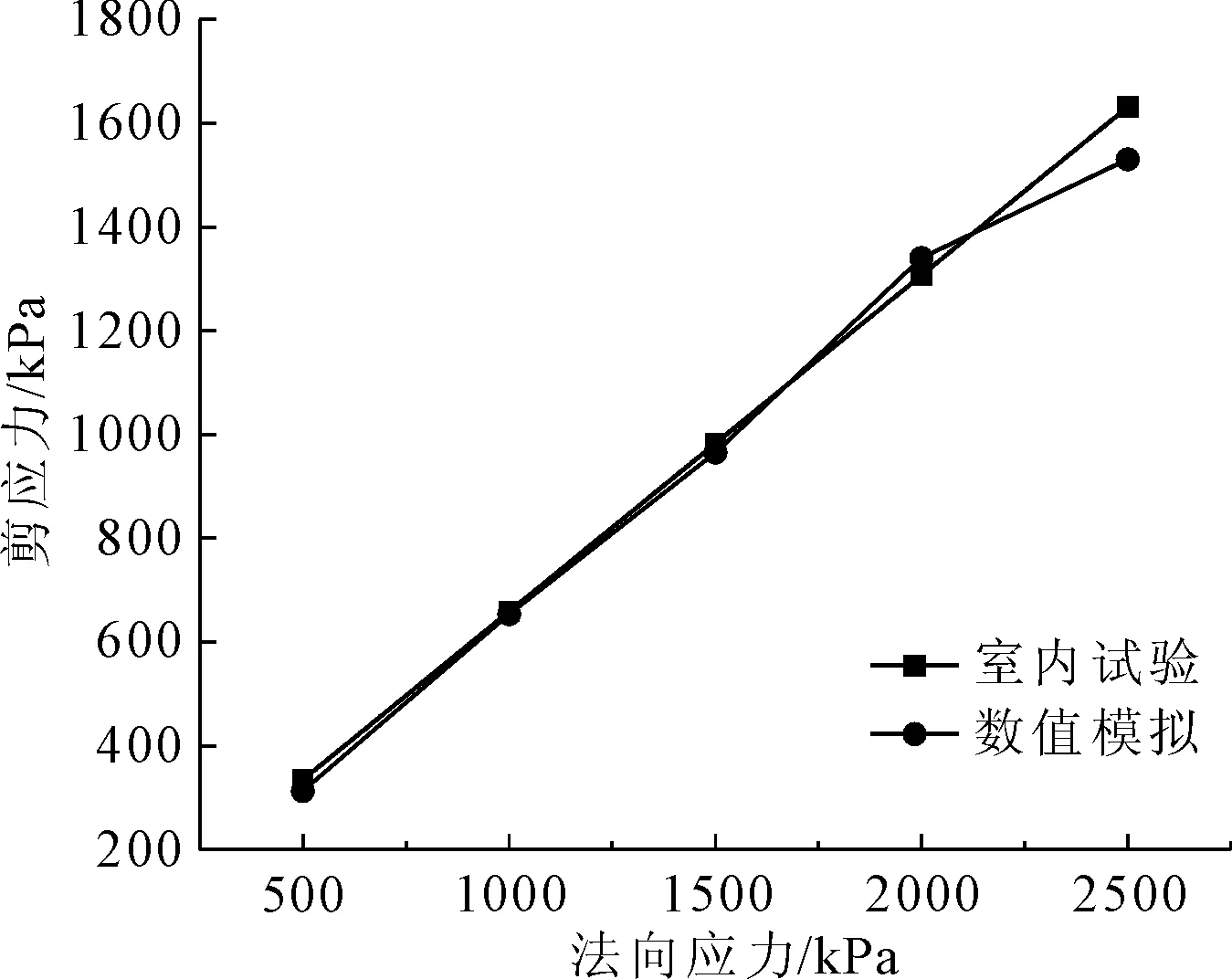
图8 室内试验和数值模拟结构面抗剪强度

表3 结构面直剪试验结果

2 滑坡数值模型

2.1 滑坡区概况

研究区历史滑坡主要是多台阶局部破坏，以圆弧破坏和楔形破坏为主。研究区域边坡于1 784 m～1 884 m台阶出现较大范围垮塌，涉及垮塌台阶10个，垮塌方量约为3.5万m3，如图9、图10所示。该段边坡是露天矿最陡的边坡，中上段平均坡角42°。通过现场调查，该区域岩层为灰岩，发育有一组倾角小于30°的顺倾向节理，与坡面小角度斜交，贯通长度几米到十几米为主。如果边坡坡度较大，容易形成一定规模的崩塌破坏，即使坡度稍缓，也容易形成台阶内的崩塌破坏。

图9 滑坡体整体状况

图10 崩塌滑坡体细部

2.2 边坡数值模型

通过无人机航拍三维建模获取研究区域包含地表色彩贴图的数值高程地图。根据穿过所有岩层，坡高最高、坡比大，能代表了该区域的最不利地层分布情况的原则选取典型剖面，见图11。典型地质剖面主要穿越地层为灰岩层，是整个矿区中最陡的部分，平均坡角达到41°。

图11 包含地表贴图的数字高程地图

根据边坡特征建立包含节理面的岩质边坡二维模型，如图12所示。坡高341.3 m，高度为183 m～313 m范围内沿坡表等间距设置5组倾角为20°的节理面。距离节理面上下各2 m处分别设置2个测量圆，用来监测节理面两侧应力、应变、孔隙率、颗粒运动和位移。其余部位沿坡表每间隔50 m距坡面的垂直距离为15 m左右设置一测量圆，依次进行编号。边坡整体采用平节理模型，结构面使用平滑模型，将室内试验标定过的自然状态下的参数代入模型中。6号—15号测量圆监测节理分布区域，1号—5号测量圆监测岩性中下部岩性较完整区域，16号—19号测量圆监测坡顶区域。

图12 典型剖面离散元模型

3 边坡数值模拟结果

3.1 整体破坏趋势分析

如图13所示，随着计算步增加，节理面上部颗粒的位移逐渐增大，下部受节理控制较小，随着上部颗粒卸载过程结束，位移趋于稳定。由于围岩完整性较好，边坡中下部基本趋于稳定，无较大位移。根据图14，当计算结束时，由于节理处颗粒间的强度较低，上层岩体受重力作用不断累积蠕滑变形，边坡节理分布区上方发生较大位移，滑面贯通，形成了滑坡体。边坡其余位置保持稳定。计算结束时，节理分布区上方测量圆的位移仍具有增加的趋势。15号测量圆靠近坡顶，其位移最小。除15号测量圆外，其余位于节理上方的测量圆位于节理上方的测量圆位移均大于节理下方。

图13 测量圆位移散点图

图14 最终状态(计算步1 000)边坡位移云图

根据图15、图16可知，滑坡体的前缘运动速度最大，节理上颗粒运动速度次之，靠近坡顶位置最低。在前缘的牵引下，节理上方的岩体沿节理加速下滑。此外，边坡中下部和坡顶没有位移，速度为0。节理分布区上放岩体逐渐沿节理面与坡体脱离，并且速度越来越快，呈上升趋势。节理分布区下方颗粒运动速度经历了初期短暂增长后，逐渐下降趋于平稳，摆脱滑坡体运动的影响。

图15 测量圆速度散点图

图16 最终状态(计算步1 000)边坡速度云图

1号—5号测量圆和16号—19号测量圆监测到坡顶和边坡中下部速度和位移基本为0。节理分布区6号—15号测量圆监测范围颗粒位移小于0.7 m之间，运动速度均小于2 m/s，且均有继续增大的趋势。随着时间推移，节理面上方颗粒的位移和运动速度大于下部且不断增大，有加速变形的趋势。根据速度和位移的变化规律，边坡破坏为受顺倾节理控制的加速滑动破坏。

3.2 内部表现分析

边坡内部应力和裂隙分布直接影响其破坏模式。边坡内部裂隙的发育、贯通导致的应力重分布是边坡失稳的主要模式。裂隙发育过程(左侧)和力链分布(右侧)如图17所示。

图17 顺倾节理分布区裂隙及力链分布图

计算步100时，裂隙快速发育，位置集中在顺倾节理之间岩桥区域，且多为张拉破坏；根据力链分布图中顺倾节理附近的拉力力链，可知节理附近产生了拉力，滑坡体的滑面将岩节理方向逐渐贯通。计算步500时，前缘区域裂隙已贯通至边坡表面，形成前缘滑动体，滑坡体其他区域也快速发育大量裂隙；节理区域的力链完全断开，滑面完全形成，上方的滑坡体与边坡基本脱离。计算步900时，裂隙发育已趋于稳定，没有明显新增裂隙；随着颗粒的移动，逐渐形成了“拱形”力链。力链是散体材料内部颗粒间作用力沿着接触网络传递的路径。节理面附近的颗粒对其上方岩体不起支撑作用，滑坡体自重依靠力链形成的拱传递到边坡体上。根据3.1节，该区域的位移和速度也较大。前缘的位移造成滑坡体其余部分失去支撑，随着计算步的增加，在滑坡体内部各个位置逐渐发育出密集的张拉裂隙，但增长速度逐渐减慢。随着裂隙的发育，颗粒间的力链断开，发生位移，形成新的力链。随着计算步的滑坡体内逐渐形成了顺倾力链，每条力链之间缺乏连接，这种结构极易产生滑动。滑坡体内部的颗粒不断位移最终形成了“拱形”力链。

如图18所示，最终状态节理面上方发育的裂隙以垂直于坡面的剪切裂隙为主，伴有少量张拉裂隙，边坡中的裂隙数增长速度逐渐降低，最终趋于0，如图19所示。坡体中的剪切裂隙削弱了颗粒间平行于坡面的连接，逐渐形成了如图20所示的“拱形”力链。这种近乎平行于坡面拱脚位于节理边缘的连续的“拱形”力链具有一定的整体稳定性，对上方岩体有一定的承载能力。若节理面强度足以维持“拱形”力链所在范围岩体的稳定，即能够承受“拱形”上方岩体重量，同时“拱形”连续完整，则该区域岩体会沿节理面整体下滑。但随着滑坡体内部不均匀滑动，“拱形”力链的“拱脚”可能逐渐破坏，滑坡体内部力链断裂，加剧裂隙发育，最终碎散。根据边坡整体破坏的特征分析，节理分布区域已经形成了滑坡体，连续的“拱形”力链不能保证边坡完整性，但滑坡体内部具有一定的整体性。

图18 最终状态(计算步1 000)边坡内部裂隙分布图

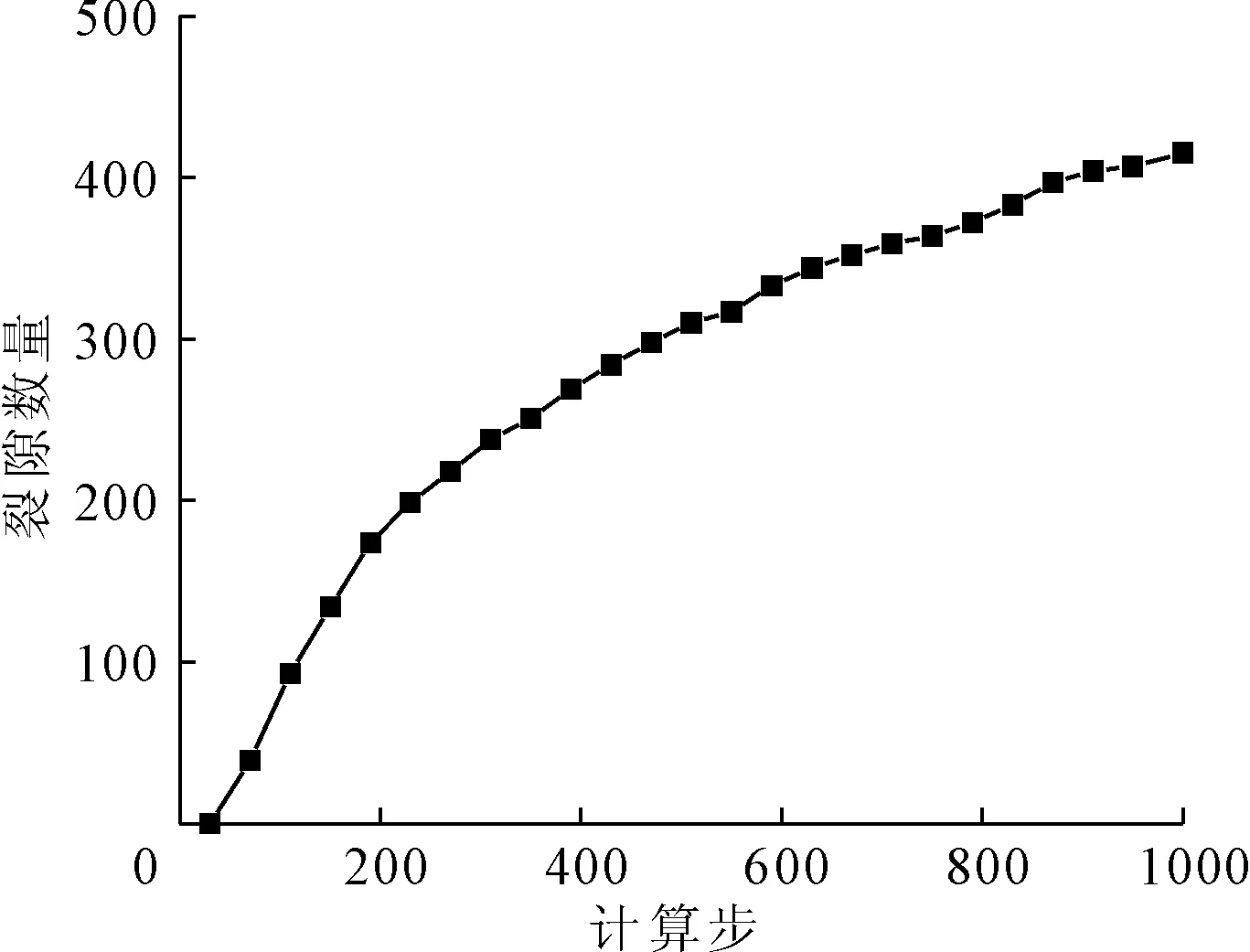
图19 裂隙数量变化图

图20 最终状态(计算步1 000)边坡内部力链图

结合速度和位移的变化规律，边坡破坏应为受顺倾节理控制的以剪切为主，辅以张拉破坏的前缘牵引滑动，裂隙的发育使节理面贯通，最终节理面上方岩体沿节理面和岩桥发生整体滑动。

4 结 语

依托露天矿边坡采用PFC2D数值分析软件建立了离散元边坡模型,并对顺倾节理岩质边坡进行了数值模拟研究，揭示了边坡的破坏过程特征:

(1)建立了岩体单轴压缩和结构面剪切模拟试验模型，通过室内试验对岩石和结构面离散元模型细观参数进行标定和验证，数值模拟结果与试验误差较小，采用PFC2D模拟岩质边坡结构面是可行的。

(2)数值模拟揭示的边坡破坏特征为：中下部节理面附近岩体发生剪切破坏和拉破坏，力链开始断裂；随着变形发展，顺倾节理处力链大面积断裂，坡体发生加速滑动，表现为以剪切破坏为主、辅以张拉破坏的牵引破坏模式；滑坡体内部形成了连续的“拱形”力链，使其具有一定的完整性，滑坡特征为沿节理面和岩桥的整体滑动。