基于多学科仿真的制动盘优化设计

方明刚，张 宁，杜利清，金文伟

（中车戚墅堰机车车辆工艺研究所有限公司，江苏常州213011）

制动盘作为轨道交通车辆基础制动装置中的重要执行部件，对其结构力学性能及热容量等均提出较高要求。现代制动盘研发流程中，依据车辆运行工况，在样品研制及台架试验前通过设计计算及仿真分析等方法，为新产品开发提供足够的设计依据，对缩短设计周期、降低研发成本起到越来越重要的作用。国内外学者在此方面开展了较多的工作，但多针对具体设计实例的仿真校核及验证等方面的研究，在最优化正向设计方面的研究尚少［1-2］。文中结合制动盘结构特点及运用实际，首先采用参数化方法实现制动盘参数化建模及多学科热—机械耦合参数化仿真，进而识别制动盘主要结构尺寸参数为设计变量，以制动盘温度及变形为约束，以制动盘质量最轻为目标开展优化设计，从而获得最优尺寸组合。

1 多学科仿真

车辆制动过程，车辆运行的动能通过制动盘与闸片之间摩擦产生的热能得以转换，该物理过程可通过在摩擦面施加随时间变化的热流密度的方式等效。

摩擦过程产生的热能主要通过热传导的形式传递至制动盘及闸片，其中大部分由制动盘吸收。制动盘吸收的热能进一步通过热对流及热辐射等方式释放到空气中。通过辐射释放的热量相对于对流换热较小，实际计算时考虑忽略。该物理过程可通过赋予制动盘散热筋及摩擦环非摩擦面等不同部位不同的对流换热系数实现对散热过程的模拟［3-4］。

通过对上述物理过程的模拟可得到制动过程制动盘的热力学仿真结果。通过提取温度等热力学仿真结果作为载荷输入，施加结构边界条件。进一步开展结构仿真模拟，获取制动盘不同部位应力及变形等结构力学结果。

2 优化设计

2.1 优化设计流程

通过建立参数化的模型，识别可驱动建模且最主要影响运用表现的结构尺寸作为设计变量，以参数化仿真模型及仿真过程，定义产品的使用要求限值作为状态变量，并定义设计目标，最终迭代执行优化设计。

对于大部分工程实践问题，目标函数及状态变量通常无法建立相对于设计变量的显式函数，一般可首先通过试验设计的方法得到一定数量的设计点，进一步拟合设计变量与目标函数及状态变量的响应曲面，从而实施优化设计。优化设计的流程如图1 所示。

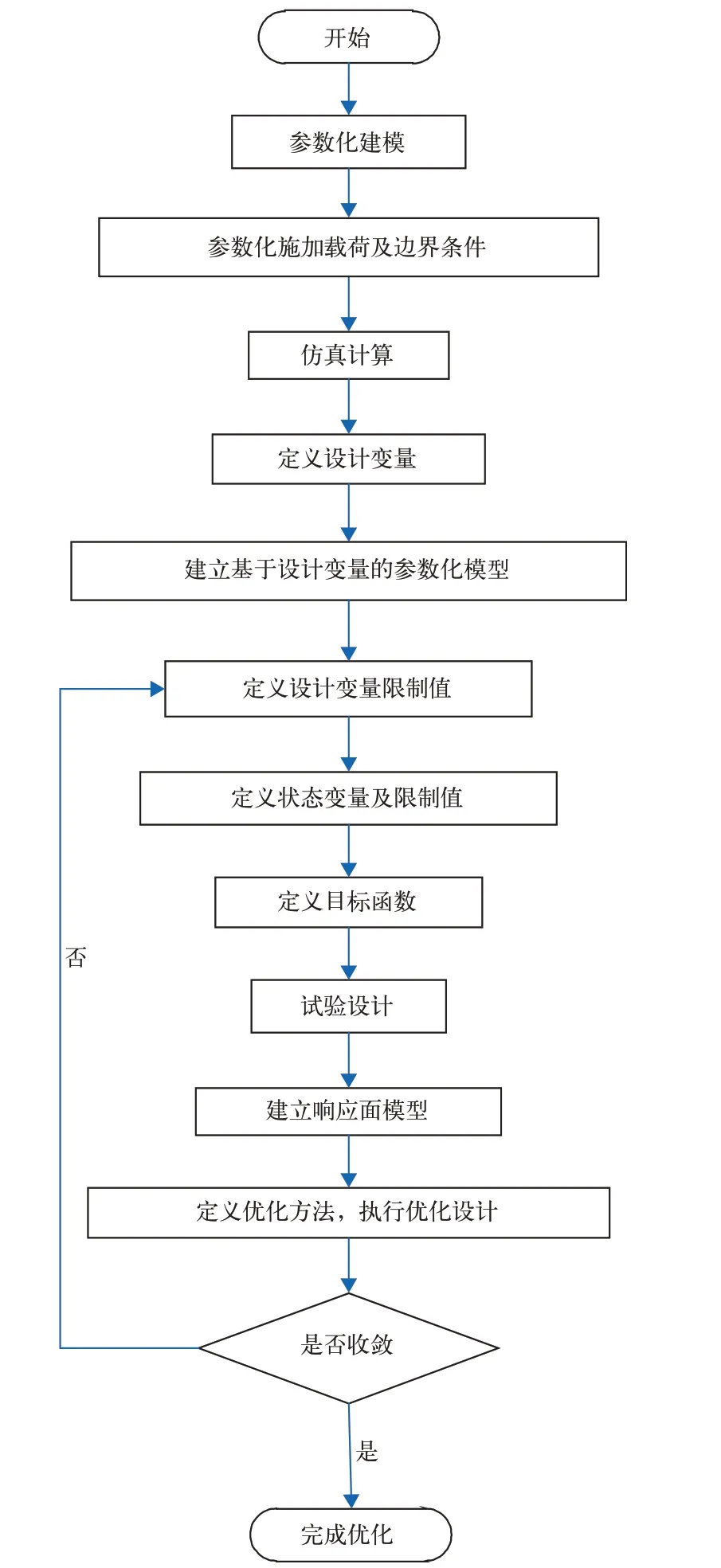
图1 优化设计流程

2.2 参数化建模

建立参数化的结构模型，是开展结构优化设计的基础。具体建模时，通常对尺寸维度较小的局部特征进行删减，在不影响优化结果的前提下降低计算成本。首先通过对模型结构及其三维特征的分析，确定所有模型特征，并形成合理的建模顺序。其次应对所有模型特征定义对应的参数，通过赋值驱动特征的建立，参数化整个建模过程。

通过对制动盘结构及模型特征的分析，以制动盘摩擦环为主要特征，通过建立参数化基本特征元素及布尔运算的方法建立其他辅助特征，搭建出制动盘特征的拓扑关系，建立了参数化的制动盘模型。

2.3 基于设计变量的参数化模型

以上建立的参数化模型中各个特征的驱动参数之间互为自由参数。建立基于设计变量的参数化模型，需创建其他所有特征的驱动参数与设计变量之间的尺寸关系式，从而在驱动设计变量构建模型时，所有模型的特征参数均被赋值。同时，在尺寸关系式中定义所有特征驱动参数的限值范围，实现所有建模特征的全尺寸封闭约束。通过约束设计变量的尺寸关系及控制驱动参数的变化范围，可以实现模型在设计变量的驱动下得以参数化构建且不产生畸变，保证所有特征的成功驱动。

综合制动盘模型特点及各特征参数对仿真结果的影响，识别制动盘外径、总厚度及摩擦环厚度作为目标参数，结合结构尺寸关系，建立上述各设计变量与其他特征参数的尺寸关系式，最终建立基于设计变量的参数化模型。

2.4 状态变量及目标函数

制动盘在实际运用过程中，摩擦面温度及盘环刚度应满足使用要求，因而定义制动过程摩擦面处的最高温度及摩擦环最外圈处的最大变形作为状态变量，结合具体制动盘材料的许用温度，给出摩擦面处温度上限，同时要求摩擦环最外圈处的变形小于最大允许变形。

随着制动盘本身材料体积的逐渐增加，其自身热容量不断提升，但同时制动盘本身质量不断增加，因此以制动盘整体质量最轻作为目标函数。

2.5 优化设计

（1）试验设计

试验设计是响应面模型构建的关键，直接关系着响应面模型的构造精度。选择合适的试验设计方法可以得到更优的试验点，从而更精确地反映输入参数与输出参数之间的关系。目前常用的试验设计方法有正交试验设计、拉丁超立方试验设计、全因子试验设计及中心组合试验设计等［5］。

（2）响应面分析

采用近似模型技术，以试验设计得到的有限量数据为基础，拟合输入参数与输出参数之间的函数关系，从而得到模型上其余未知点的响应函数。通过响应面分析方法可实现对试验因素的各水平的连续分析，从而得到各试验因素相应水平的响应值，为获取最优解提供依据。

由于各种类型的函数均可采用多项式逼近，因而多项式响应面模型可以拟合各类非线性问题，在优化设计中应用广泛［6］。

（3）优化设计

选择合适的优化算法，并定义一定的优化样本数执行优化设计。由于已完成响应面分析，所有优化样本将通过响应面快速获得而无需进行求解计算。同时，针对不同状态变量及目标函数，可定义不同的优化设计权重。

优化设计通常得到最优解集，可根据各目标函数结果改进优化的差异情况选择具体设计结果［7］。

3 仿真实例

3.1 热—结构耦合仿真

某车辆在AW3 载荷状态、平直道条件下实施连续2 次纯空气紧急制动，其制动参数见表1。

表1 车辆制动参数

拖车每轴布置2 套轴装制动盘，并采用某型号铸铁材料，初始设计的制动盘结构参数见表2。

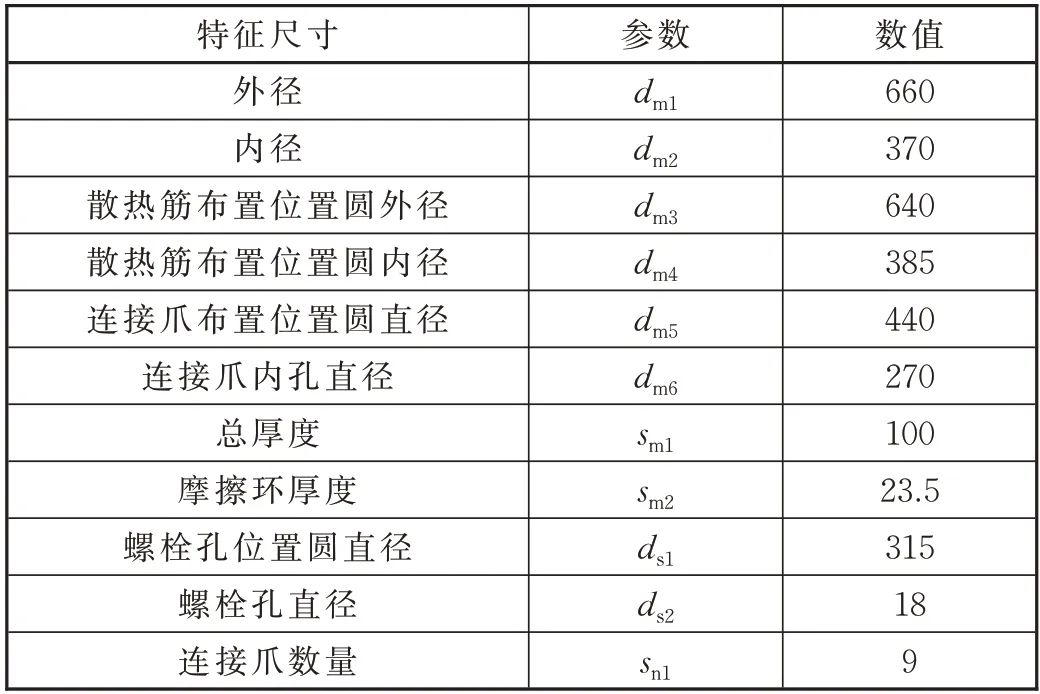
表2 制动盘参数 单位：mm

通过热力学计算得到制动盘摩擦面最高温度为261.28 ℃，进一步通过结构力学仿真得到摩擦环最外圈的最大变形量为0.743 mm。初始设计的制动盘质量为106.78 kg。

3.2 优化设计

定义设计变量制动盘外径dm1、总厚度sm1及摩擦环厚度sm2，并确定各设计变量的上下限值。定义摩擦面最高温度不超过350 ℃，摩擦环最外圈处最大变形不超过1 mm，并以制动盘总质量最小为目标函数。

从而得到制动盘优化设计数学模型为式（1）：

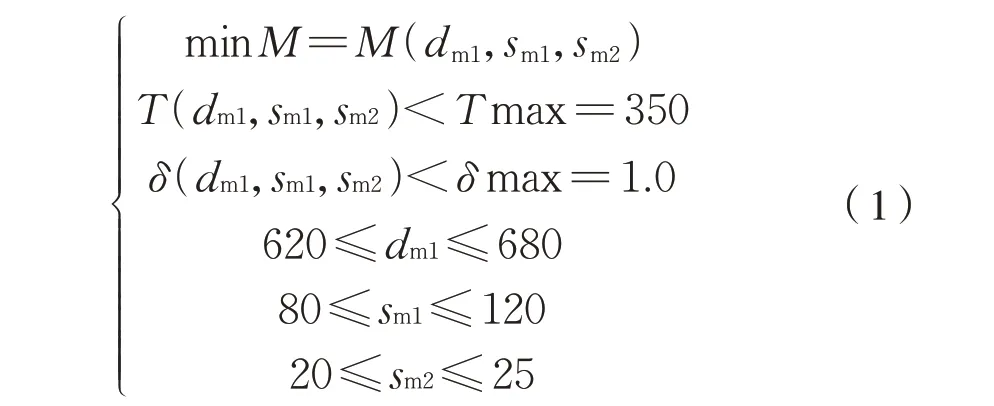
取5 个水平，得到设计变量的因素水平表见表3。

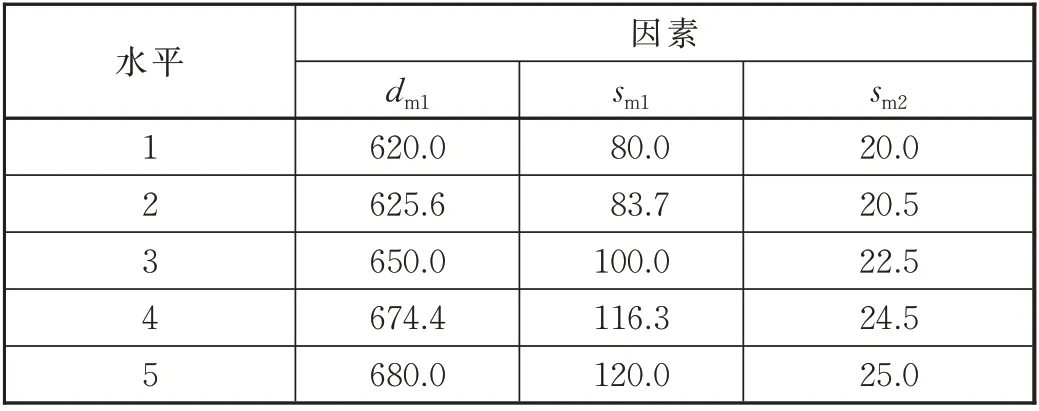
表3 因素水平表 单位：mm

采用中心组合设计法计算得到不同设计点，见表4。

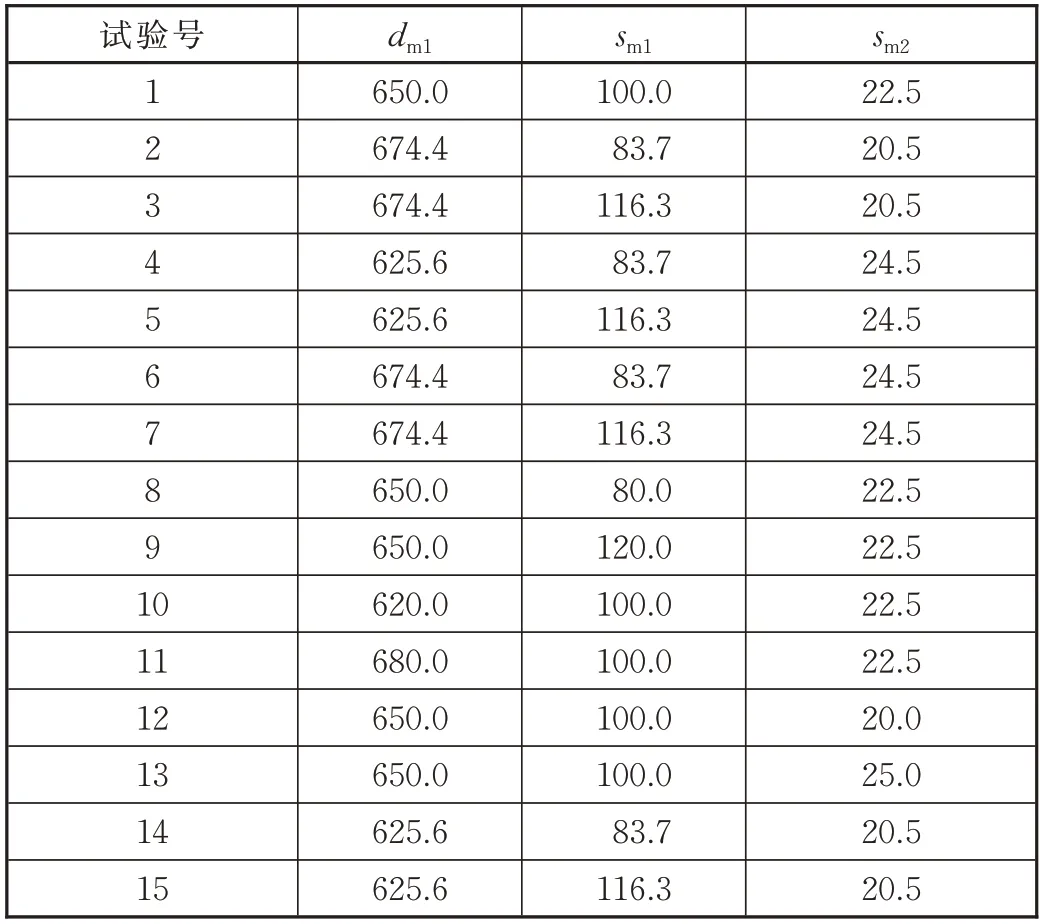
表4 试验设计方案 单位：mm

采用完全二次多项式法建立响应面模型，并定义100 个优化样本数执行优化设计，得到基于指定目标设计变量的3 组候选设计点表，见表5。

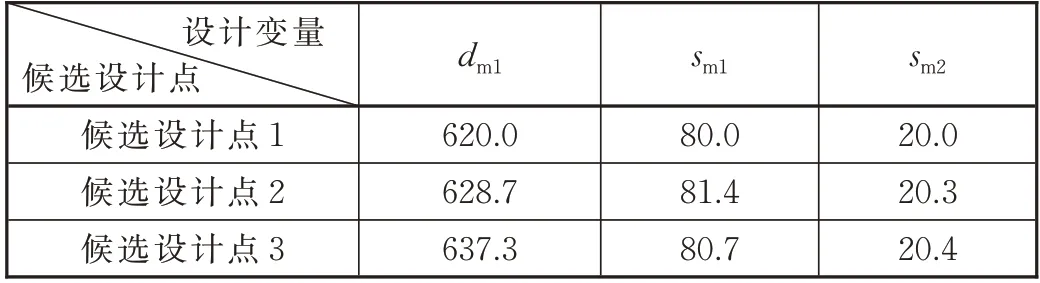
表5 候选设计点 单位：mm

3.3 优化结果

以候选设计点3 为例，采用该组优化结果计算得到制动盘摩擦面最高温度为280.68 ℃，温度云图如图2 所示；摩擦环最外圈的最大变形量为0.844 mm，变形云图如图3 所示。制动盘质量为88.23 kg。

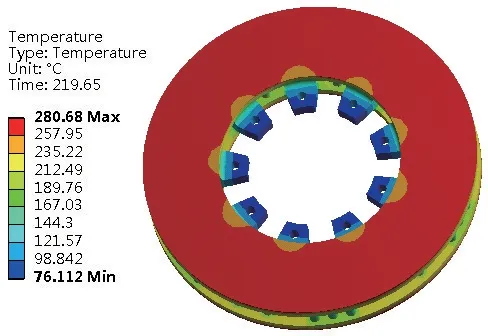
图2 制动盘温度云图

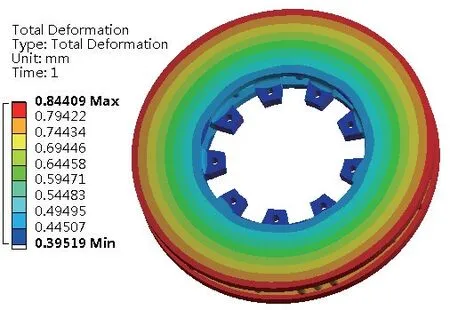
图3 制动盘变形云图

与初始设计仿真结果对比可以发现，采用候选设计3 中各设计变量建立的制动盘，其摩擦面最高温度及摩擦环最外圈的最大变形量略有升高，但制动盘质量减少较多，材料利用率提升较大，优化效果明显。

4 结 论

（1）梳理了制动盘多学科仿真及优化设计的流程，实现了制动盘参数化建模，建立了基于设计变量的参数化模型，并定义了状态变量及目标函数。

（2）采用某一具体制动盘运用实际开展了基于热—机械耦合的优化设计，结果表明了优化设计方法的可行性及有效性。

（3）提升了制动盘设计及验证手段，为制动盘及其他车辆制动部件的优化设计提供了新的设计方法及思路。