曲率半径对曲桥地震最不利输入方向影响研究

董 晨，邓通发

(江西理工大学 土木与测绘工程学院，江西 赣州 341000)

0 前 言

我国陆地总面积约960万km2，其中山地、高原和丘陵约占总面积的67%，这导致了我国桥梁形式的多样性,曲线梁桥在我国应用非常广泛。同时，我国地处环太平洋地震带和欧亚大陆地震带，使得我国的地震灾害频发，因此，研究曲线梁桥的抗震性能对于我国的桥梁发展具有极其重要的意义。曲线梁桥由于其结构的复杂性和不规则性，其受力特点也比较复杂，主要有：①在结构自重作用下，除支点截面以外，曲线梁桥外边缘的挠度一般大于内边缘的挠度；②在自重和外荷载作用下，梁截面在产生弯矩的同时，也会产生“弯-扭”耦合作用；③对于两端均有抗扭支座的曲线梁桥，其外弧侧的支座反力一般大于内弧侧，所以曲线梁桥抗震分析较规则直线桥更复杂，其中的难点之一就是最不利输入方向的确定，因此，研究曲线梁桥的最不利输入方向显得尤为重要。

1 曲线梁桥最不利输入方向研究现状

目前，我国规范[1-2]规定对曲线梁桥抗震分析中地震波的输入方式为分别沿两桥台连线的弦线方向及水平面内与之垂直的方向输入，当用曲梁单元模拟分析时，仅需考虑以一联中的两端连线方向及其垂线方向的水平地震输入，分别得出两个方向的最大地震反应后，再根据组合方法来确定最不利地震反应。张文学等[3]通过分析地震动输入角度对规则(墩高相等)和非规则(墩高不等)曲线梁桥地震响应的影响时发现：对于规则曲线梁桥，采用规范上的输入方式较合理；而非规则曲线梁桥，最不利值不一定出现在割线和垂直割线方向。丁印成[4]比较了沿曲线梁桥整体正交方向输入及沿每个桥墩切向和径向进行正交输入(称为全方向输入)两种地震波输入方式，认为两种输入方向下，某些桥墩的最大值和最小值相差近90%，所以在分析曲线梁桥等复杂结构的桥墩上的地震响应时，采用全方向输入方式更合理。冯云田等[5]认为无论简单或复杂结构，只需沿任意两个不重合的方向(为计算方便取垂直方向)输入地震动，经过少量计算，便能得到各点或截面的地震最大响应值和地震输入主方向。Abdel-Salam等[6]对比了反应谱分析法和时程分析法，认为反应谱法不能将曲线桥高频振动模态对结构的影响考虑进去，建议按照时程分析法进行结构抗震设计。现行的《公路工程抗震设计规范》(JTG B02—2013)在对桥梁进行地震作用计算时，主要采用截面内的最大内力(弯矩)进行设计，实际上自从E.L.Wilson等[7]于1982年首先提出了关于地震动主方向问题的讨论,大部分学者均以位移或内力(包括弯矩、剪力和轴力)的最大响应的方向作为最不利输入方向的准则。例如，lopez[8]和penzien等[9]认为扭矩、弯矩等内力响应最大值所对应的方向即为最不利输入方向；滕军等[10]分别以径向或切向的内力最大、位移最大作为判别最不利输入方向的准则；全伟[11]则以曲线梁桥桥墩顶的径向和切向位移最大值作为判别最不利输入方向的准则。

在曲线梁桥设计以及地震响应分析和抗震设计过程中，由于各种原因，不可避免地需要对曲线梁桥的这种参数进行优化调整，而结构参数的调整可能会引起地震最不利输入方向的改变，反复改变地震输入方向会给结构优化带来巨大的麻烦。因此，有必要研究地震作用下，曲线梁桥的最不利输入方向随着参数调整的变化规律，从而明确对曲线梁桥最不利输入方向有显著影响的关键参数。本文采用时程分析法，研究曲线梁桥在单维EL-Centro地震波的激励下，曲率半径对其墩底受剪力作用的径向与切向分效应的影响。

2 曲线梁桥数值模型的建立

本文选取的曲线梁桥整体布置及主要构件的截面尺寸如图1所示。该曲线梁桥为三跨曲桥，其曲率半径为50 m,每跨跨径均为20 m；上部结构采用单箱单室箱梁，材料为C50混凝土，曲梁宽为8.5 m,高为1.9 m。下部结构中，联端采用双柱墩，中间采用独柱墩，墩柱材料全部为C40混凝土，且墩高均为8 m,曲桥联端桥墩直径为1.2 m,中间桥墩直径为1.5 m,全桥采用板式橡胶支座，其中，支座竖向刚度认为无穷大，横向刚度为3 000 kN/m。

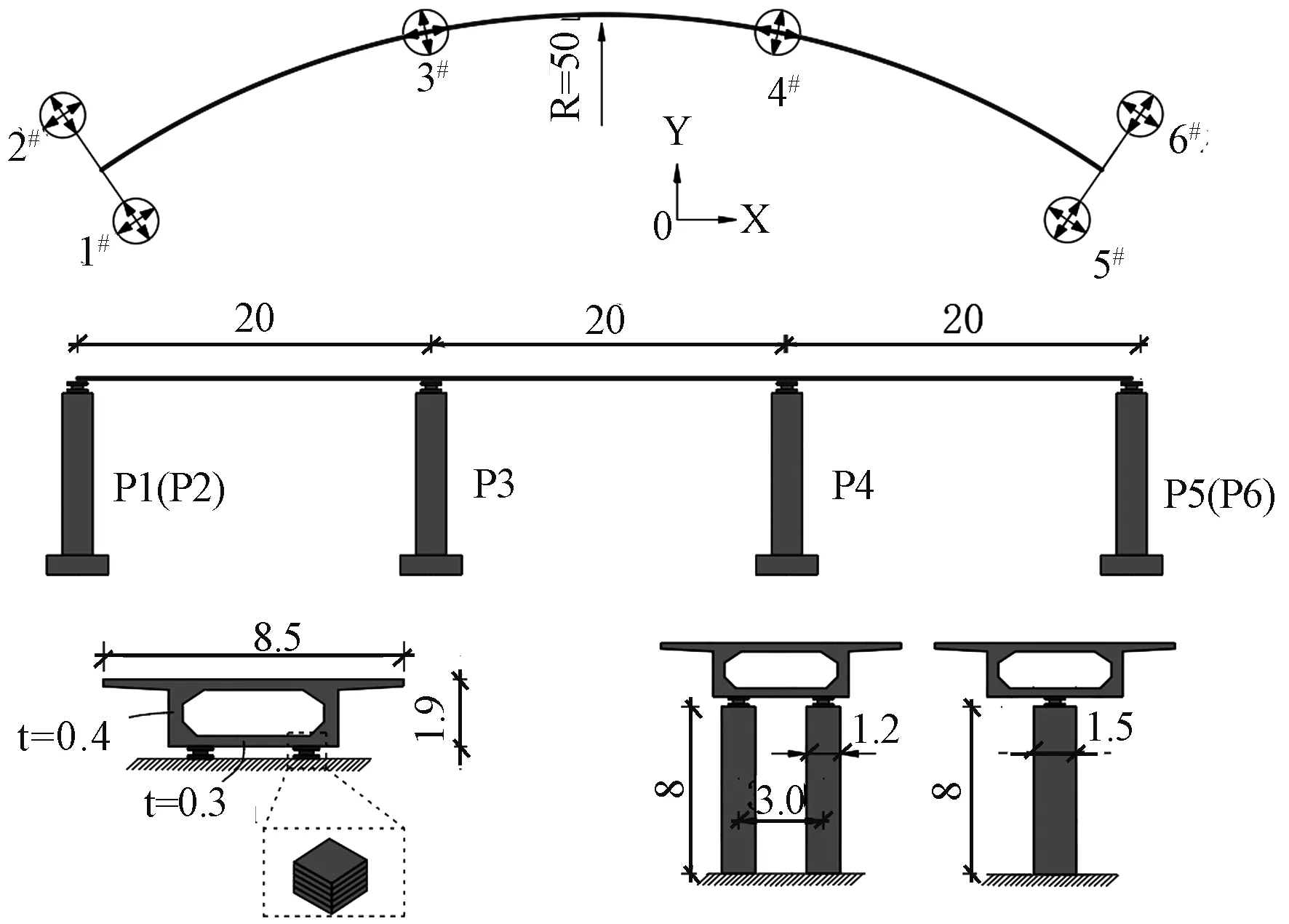
图1 曲线梁桥整体布置及截面尺寸图(单位：m)

本文采用SAP2000进行曲线梁桥有限元建模，该模型中，主梁采用板壳单元模拟，桥墩采用弹性梁单元模拟，支座采用线性连接单元模拟，不考虑桩-土间相互作用对结构的影响，墩底采用固结方式进行处理。

本文中，θ为地震输入方向与整体坐标系中X轴的夹角，θ沿逆时针方向旋转为正，因为文中的曲线梁桥的几何布置关于Y轴对称，故令0°≤θ≤180°。本文以P2,P3墩的墩底剪力为核心指标来确定曲线梁桥的最不利输入方向。

3 曲线梁桥对不同参数的敏感性研究

改变曲线梁桥的曲率半径，分别取R=20、30、80、120、200 m和∞(直桥)，分别研究这些参数的改变对曲线梁桥墩底剪力在径向与切向分效应的影响，结果见表1～2和图2。

表1 不同曲率半径情况下构件径向分效应对地震输入方向的敏感性

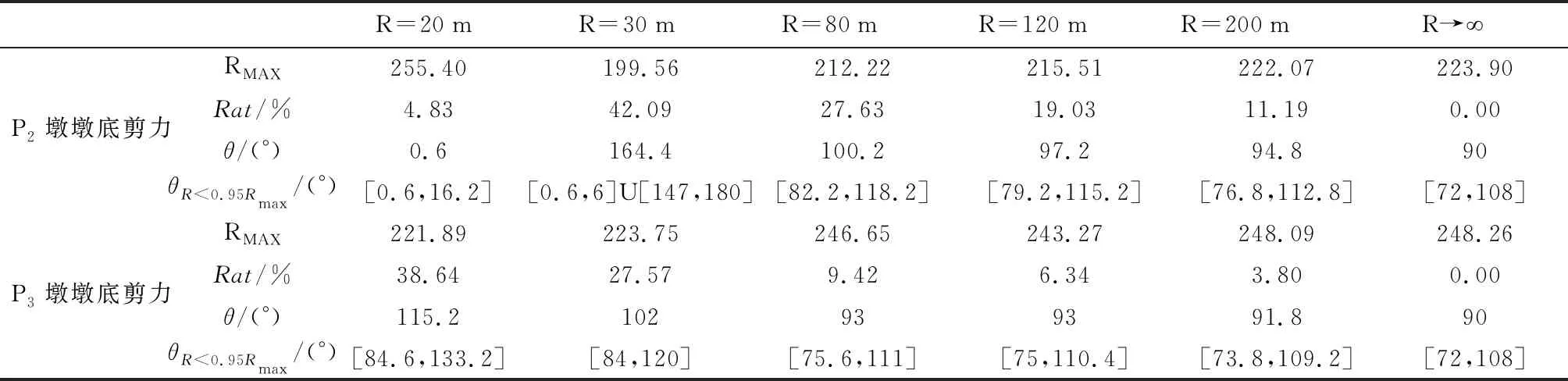
表2 不同曲率半径情况下构件切向分效应对地震输入方向的敏感性

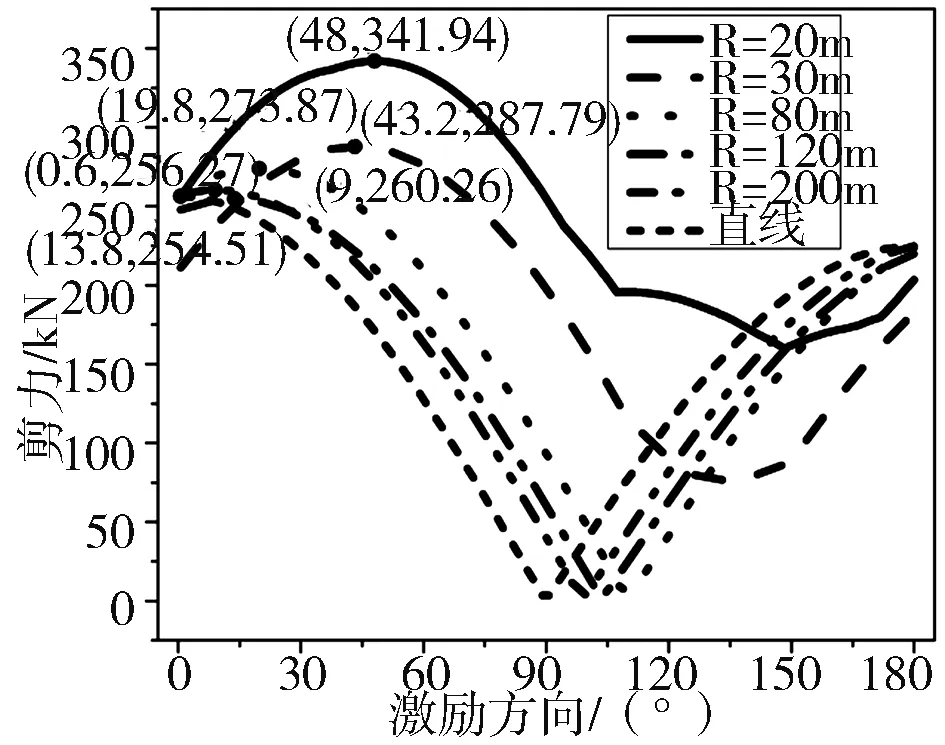
(a)P2墩底径向剪力

根据表1～2及图2，可以得出：①地震输入方向对分效应的影响幅度和最不利输入角容忍度范围随着曲率半径的增大而减小，说明随着曲率半径的加大，输入的方向对于曲线梁桥分效应的影响更加重要；②径向与切向的分效应的峰值随着曲率半径的增大而减小，且减小的幅度越来越小，逐渐趋于稳定；③曲线梁桥的径向与切向的最不利输入角度相差基本为90°，说明曲线梁桥的最不利输入方向为统一方向；④曲率半径对P2墩墩底剪力最不利输入方向的影响比其对P3墩墩底剪力最不利输入方向的影响小，说明中墩的敏感性高于边墩。

4 结 论

曲线梁桥的最不利输入方向为统一方向，随着曲率半径的增大，曲线梁桥墩底剪力分效应逐渐降低并趋于稳定。此外，曲线梁桥径向与切向受剪力作用的分效应对于曲率半径的敏感性较强，且中墩对于曲率半径的敏感性高于边墩。

[ID:012830]