多孔网幕泡破压力预测模型的建立及实验验证
王晔,张婉雨,汪彬,耑锐,任枫,蔡爱峰,杨光,吴静怡
(1 上海交通大学机械与动力工程学院,上海 200240; 2 上海宇航系统工程研究所,上海 201109)
引 言
随着探月、探火工程等深空探测任务的不断发展,高性能动力系统已成为实现深空高效轨道转移及运输的基础条件。低温推进剂因其高比冲的特点被认为是未来空间应用中的首选推进剂之一。在地面常重力环境或是空间加速飞行过程中,低温推进剂贮箱中的气液两相因密度差异自发出现相分离现象。而在空间滑行阶段,体积力作用不明显,贮箱内气液两相均匀混合且相分布不确定导致气液分离困难,若直接输送夹气燃料将导致发动机启动失效。常温推进剂在轨管理技术已经相对成熟,主要有惯性式、挠性隔膜式、电磁式等分离技术。然而,低温推进剂具有低沸点、低潜热、贮运成本高等特点,现有的相分离方式不再适用[1]。表面张力驱动式分离技术充分利用微重力环境下起主导作用的表面张力,不受低温流体蒸发的影响、无须消耗多余燃料,是一种极具前景的低温推进剂气液分离技术。金属网幕由于其比表面积大、物理稳定性高等优点,广泛应用于低温推进剂气液分离中,例如网幕通道式液体获取装置(liquid acquisition device, LAD)[2-3]、气口相分离装置(gas port phase separator, GPPS)[4-5]等。以网幕通道式LAD 为例,液体在压差作用下能够穿过多孔网幕进入液体输运通道,而气体因微米级孔隙中的液体毛细力而被阻挡于多孔网幕之外。由此在多孔网幕处实现了气液分离,可将纯液推进剂输送至发动机进液通道,保障发动机平稳启动。
泡破压力(bubble point pressure)定义为气泡突破多孔网幕束缚时所对应的两侧临界压差,是影响网幕相分离性能的最重要参数[6-7]。泡破压力越大,网幕的相分离性能越好,实际运行中纯液推进剂的获取效率越高。泡破压力与液体表面张力、接触角和网幕的等效泡破孔径有关[8]。然而多孔网幕的孔隙结构极其复杂,其等效泡破孔径难以直接测量[9-11]。现有的泡破孔径计算方法主要有以下三种:一是参考流体计算法,即测量标准参考流体的泡破压力,根据泡破压力、表面张力、接触角直接反算其泡破孔径,参考流体计算法的最大优点是一次泡破实验即可确定孔径,但是对实验测量过程的准确性要求极高;二是斜率计算法[12],即采用不同流体进行多次实验,以表面张力和泡破压力为横纵轴,根据数据趋势线的斜率计算泡破孔径,相较于参考流体计算法,斜率计算法的准确性更高,但是这种方法需要对每一种规格的网幕都进行多次泡破实验,工作量巨大[13];三是扫描电镜(scanning electron microscopy, SEM)图像法,即直接根据SEM 拍摄的网幕表面形貌图像来估算其孔径,公开文献中基于SEM 法获得的泡破孔径数据较少,且计算结果与斜率计算法的误差高达37%[13-14];这是因为仅依靠表面形貌图像无法表征实际的三维孔隙结构和气液交界面形状,所获得的泡破孔径结果具有较大误差[14-15]。
综上所述,多孔网幕的泡破孔径计算仍然未有通用且高效的方法。一方面,现有研究方法大多基于泡破压力实验,对实验准确性要求较高,且需要对多种工质进行实验,测量过程耗时长[6,13,16]。另一方面,当无法进行泡破实验时,扫描电镜图像法是目前唯一获得泡破孔径的方法,然而其准确性较差[14-15],无法推广。因此,建立一种简便可靠的泡破孔径测量方法势在必行。本文基于多孔网幕的三维孔隙结构,对气泡突破网幕时的孔隙截面沿流向的变化过程进行分析,建立一种多孔网幕静态泡破压力的通用型预测模型,同时,本文搭建了可视化泡破压力测试实验系统,以证明该解析模型的准确性和对低温工质的适用性。
1 理论分析
1.1 泡破压力模型
斜纹密纹多孔网幕的几何结构和SEM 图像如图1所示。斜纹密纹网的特点是经线直径及间距远大于纬线直径及间距,经线数量较少,纬线数量较多。直径较大的经线始终保持水平,较细的纬线紧密排列,交错穿过两根平行排布的经线,获得的多孔网幕编织紧密,具有较小的孔隙率和孔径。多孔网幕规格以nw×ns的方式命名,nw和ns表示单位英寸长度下的经纬线数目。图中lw和ls表示经纬线间距,dw和ds表示经纬线径,通过对不同规格网幕的详细扫描电镜图像分析,证明了多孔网幕的实际结构与制造结构具有一致性。
相分离装置正常运行过程中,气体因微米级孔隙中的液体毛细力而阻挡在多孔网幕之外。但在极限状态下,气体沿z方向穿过网幕将导致相分离失败。图2展示了多孔网幕内气泡突破过程的示意图。液体在毛细力的驱动下完全润湿网幕孔隙,气体在压差作用下会将气液交界处的弯月面沿孔隙通道向上推动[图2(a)]。弯月面在孔喉处曲率最大[17],此时需要更大的压差才能将弯月面进一步推动[图2(b)]。一旦弯月面通过孔喉,气体就能在压差作用下完全穿越孔隙通道,此时可以在液体侧观察到突破网幕的气泡。根据Young-Laplace 方程,将多孔网幕等效成一组毛细管,将泡破压力表征为弯曲界面处的压降,则静态泡破压力表达式可以简化为[8,13]:

图2 网幕孔隙和气泡突破过程的示意图Fig.2 Schematic diagram of pore channel and bubble breakthrough process across a metal wire screen

式中,σ是流体的表面张力;θ是流体在不锈钢表面的接触角;Dp是泡破孔径,即将多孔网幕中的孔隙通道等效成一个毛细管所对应的有效孔径,与多孔网幕的编制结构和规格有关。因此,多孔网幕的静态泡破压力直接依赖于其孔喉处的孔径。对多孔网幕的几何结构进行建模,获得实际三维孔隙是建立泡破压力预测模型的重要基础。
1.2 多孔网幕的孔隙结构分析
对于任意结构已知的多孔网幕,其等效泡破孔径均可以根据三维孔隙结构分析获得。以编制结构最复杂、应用最广泛的斜纹密纹网(图1)为例,以经线的中轴线为原点,作xy平面沿z轴的剖面图,图3 展示了孔隙形状沿气体流动方向的变化过程。图中灰色阴影区域为网幕的固体结构剖面,蓝色区域为气体可以流通的孔隙处。根据孔隙形状的变化过程可以看出,多孔网幕的孔隙并不是一个严格意义上的圆柱体通道,各孔隙间由三维孔道相互连通[图3(a)~(c)]。而在z=ds/2+dw/2 截面,即图1(a)中的横截面A—A 位置时,原本相互连通的孔隙被紧密相切的纬线阻断,形成多个异形平行四边形的孔隙截面。此处就是多孔网幕的孔隙通道中孔径最小的位置,如图3(d)所示。随后,由于相切的纬线在圆弧处产生的间隙,孔隙之间再次相互连通[图3(e)]。因此,图3(d)中的异形孔隙即为多孔网幕的孔喉位置,也是决定网幕泡破压力的关键孔隙截面。

图1 多孔网幕325×2300的几何编织结构Fig.1 Schematic diagram and SEM image of the metal wire screen 325×2300

图3 孔隙形状沿气体流向的剖面图Fig.3 Cross section views towards z direction showing the shape of the pore channel
2 基于孔隙尺度建立泡破压力预测模型
基于三维孔隙结构分析,将多孔网幕等效成毛细管并定量化表征其泡破孔径,建模过程中做出如下假设:(1)多孔网幕的纬线紧密相切;(2)经纬线均视为圆柱体,经纬线间互不干涉,不存在变形。基于上述假设,以图3(d)中黄色标记展示的一个典型异形孔隙截面为例,图4 展示了该孔隙的几何结构和经纬线编制结构示意图。如图4(a)所示,异形孔隙由四根相切的纬线构成,①号和④号纬线位于两根经线的上方,并在排布过程中存在偏移角度α。因此,其z=ds/2+dw/2 截面是沿中轴线相切得到的近长方形截面。②号和③号纬线以角度β环绕过经线,并交错穿插于相邻经线之间,如图4(b)所示。因此在z=ds/2+dw/2 处,②号和③号纬线随经线弯曲呈现出椭圆截面。最终获得的异形孔隙的上下边由直边-斜边-直边组成的折线——-AB构成,孔隙的左右两侧边则由椭圆的半周长构成。
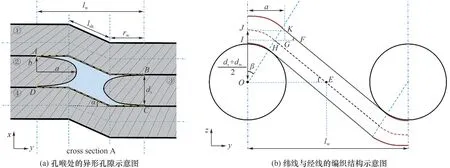
图4 泡破孔径计算的示意图Fig.4 Illustration of the effective bubble point diameter at the pore throat
基于孔隙的几何结构,可以将异形孔隙截面等效为毛细管所对应的有效孔径,进而获得泡破孔径的定量化表达[13]:


最后,将异形孔隙的面积和周长公式[式(3)、式(4)]、侧边公式[式(5)]以及椭圆长短轴公式[式(6)、式(7)]代进式(2)中,即可得到多孔网幕孔喉处的等效泡破孔径:

公式中涉及的经线径dw、纬线径ds、经线间距lw均为网幕的制造参数,在网幕编制时即确定;偏移角度α和环绕角度β可以由式(8)和式(10)求解。将等效泡破孔径的计算式代入式(1)中,最终获得斜纹编织密纹网的静态泡破压力预测模型:
至此,本文基于斜纹密纹网幕的孔隙尺度结构,得到了其静态泡破压力的解析模型。对于任意规格的多孔网幕和流体工质,只要知道网幕的结构参数(经纬线径、经线间距)和流体的表面张力及接触角,其静态泡破压力就可以完全确定,不依赖于实验测试。
3 模型准确性验证
为验证本文建立的静态泡破压力预测模型的准确性,搭建了可视化泡破压力测试实验系统。该实验系统由可视化实验管段、高速相机、压差传感器、气体质量流量控制器和数据采集系统组成,如图5所示。实验管段被网幕组件分为上下两个部分,下管段是由实验腔和润湿网幕组成的封闭腔体,上管段直接与大气连通。网幕组件以凸台压紧的方式组装进实验腔内,以保证网幕上下的实验管段光滑,便于相机记录气泡突破过程。压差传感器布置于网幕上下两侧,用于记录封闭实验腔与大气环境之间的压差。每次实验时,用实验工质将多孔网幕完全润湿,使网幕表面形成液膜,并在网幕上方进行液封,保证网幕与下管段组成一个完全封闭的实验腔体。预实验结果表明,通气速率为5、1 ml/min的泡破压力测量结果之间的偏差小于1%,证明在该范围内通气速率对泡破压力测量结果的影响极小。综合考虑实验效率和结果准确性,最终选择5 ml/min的通气速率将气体经气体流量控制器通入下管段,给封闭实验腔缓慢增压,保证封闭腔体的准静态过程[17],确保静态泡破压力测量结果的可靠性。同时将进气口布置在下管段底部,以保证泡破过程不受腔体内流场变化的干扰。数据采集系统和高速相机实时记录网幕前后的压差信号和气泡行为。泡破压力测量实验中使用的单晶硅压差变送器的型号为MeaconⓇMIK-501,气体流量控制器的型号为AlicatⓇMC-100SCCM,数据采集仪的型号为AgilentⓇ34970A,采集频率为3 Hz,高速相机使用YVisionⓇOSG030-815UM 工业相机,帧率为815 帧/秒。压差传感器的量程及精度为(20.000±0.015)kPa,温度测量误差为±1 K,实验工质表面张力的不确定度可以通过物性模型在Ttest±1 K之间的差值计算,接触角的测量误差为2°。每组流体-网幕测试进行三次重复实验,以减小测量过程中产生的实验误差。

图5 泡破性能实验系统及实验装置Fig.5 Experimental apparatus of bubble point pressure measurement
图6展示了测量过程中多孔网幕两侧压差随时间的变化曲线和泡破现象。在实验初始阶段,气体以恒定速率均匀注入封闭实验腔中,ΔP呈线性增加的趋势。当高速相机记录到第一个气泡突破网幕时[图6(b),首次突破],压差信号在ΔPbp处出现明显拐点,此时网幕前后的压差即为其泡破压力。随后,大量气泡从开放的孔隙通道中溢出(连续突破),网幕两侧压差逐渐回落,直到进气加压过程和泡破过程达到动态平衡。关闭进气阀门,停止对下管段加压后,气泡的突破速率减慢(间歇突破),最终气泡突破停止。本文以325×2300网幕为例,测量了流体工质水、HFE 7500、航天煤油的泡破压力,以验证本文建立的泡破压力预测模型的准确性,实验工质的物性参数如表1所示。

表1 101 kPa和20℃环境下实验工质的物性参数Table 1 Physical properties of the fluids at 101 kPa and 20℃

图6 泡破压力测量过程的实验结果和泡破现象Fig.6 Pressure difference during bubble point pressure measurement and images from high-speed camera at different periods
进一步收集了文献中基于实验获得的泡破孔径数据11组,涉及7种不同规格的多孔网幕,将文献中根据实验数据反算的泡破孔径值与基于本文式(11)计算的有效泡破孔径进行对比。表2展示了有效泡破孔径的模型预测值与实验测量值的对比结果。可以看到,本文预测模型与公开文献中实验测量值的平均误差仅为8%,最大误差在20%以内,证明了本文泡破孔径计算公式的准确性和对不同网幕规格的适用性。同时,模型预测结果与实验数据的一致性进一步证明了对于多孔网幕这一复杂的周期性排布结构,其等效泡破孔径是可以根据其孔隙尺度结构直接理论计算得到的。该解析表达式能在不进行实验的情况下有效预测多孔网幕的泡破孔径,且具有较高的准确性,大大简化了泡破实验测量过程。
另外,造成等效泡破孔径预测值与实验值偏差的原因主要有两点。一是实验数据的准确性。从表2 可以看出,200×1400 和325×2300 网幕的数据来源广泛,不同研究者们多次的测量过程降低了实验测量结果的偶然误差,因此模型预测值与实验测量值的误差较小。二是多孔网幕的制造误差。本研究在孔隙结构建模过程中做了将经纬线均视为圆柱体,且经纬线间互不干涉,不存在变形的假设。然而在实际生产过程中,经纬线均是由微米量级的金属丝线编织而成,金属丝线不可避免地会存在轻微的拉伸变形情况,这也会引起模型预测结果与实验数据之间的偏差。

表2 等效孔径的模型预测值与实验测量值的对比Table 2 Comparison between the measured and the predicted value of the effective bubble point diameter
除了对不同网幕规格的适用性,预测模型对不同工质的适用性也是一个重要考量指标。低温工质和常温工质的物理性质差异较大,低温工质具有低表面张力、低密度、低黏度等特殊物性。为验证本文泡破压力预测模型对低温工质的适用性,以200×1400 和325×2300 网幕为例,收集了文献中低温及常温工质在多孔网幕上的泡破压力实验数据250 余组,数据包含水、煤油、异丙醇、乙醇等常温工质,以及液氮、液氢、液氧、液态甲烷等低温工质[21-30]。图7 展示了基于泡破压力模型[式(12)]的预测值与文献、本文实验数据的对比。可以看出,泡破压力(ΔPbp)与表面张力(σcosθ)成正比,证明了基于Young-Laplace 方程将多孔网幕等效成毛细管的有效性,证明简化模型[式(1)]能够准确预测多孔网幕的泡破压力。对比结果表明,本文的泡破压力解析模型的预测结果与低温、常温工质的实验结果均吻合良好,平均误差均小于10%。已有研究证明,网幕的几何结构受温度的影响较小,在液氢温区,网幕孔隙的最大收缩量小于0.7%[21-22]。因此,基于三维孔隙结构推导的解析模型受低温工质的影响极小,证明了本文模型对低温工质和常温工质的适用性。该解析模型的最重要意义在于能够在没有实验数据的情况下,有效预测多孔网幕的等效泡破孔径,进而预测其泡破压力。

图7 泡破压力的实验数据与模型预测值比较Fig.7 Comparison between the experimental value and the predicted value of bubble point pressure
4 结 论
针对影响相分离性能的关键参数泡破压力,本文建立了一种基于三维孔隙结构的多孔网幕静态泡破压力的通用型解析模型。该模型可以根据网幕几何结构和流体物性参数直接预测其泡破压力,大大简化了泡破实验测量过程。以编制结构最复杂、应用最广泛的斜纹密纹网为例,多孔网幕的三维孔隙结构模型表明,其静态泡破压力直接依赖于其孔喉处的孔径。模型预测结果与本文实验、文献中的实验数据对比结果表明,该模型的平均误差仅为8%,最大误差在20%以内。一方面证明了基于Young-Laplace 方程的静态泡破压力模型的有效性,另一方面也验证了该解析模型的准确性和对不同网幕规格、常温和低温工质的适用性,能够为基于多孔结构的表面张力式液体获取装置的设计与性能预测提供参考。后续可以在该静态泡破压力预测模型的基础上进行优化,对加压速率产生的惯性力项进行修正,进一步开展高流速时的泡破压力预测模型研究。

