度量偏好直觉模糊序决策信息系统的分布约简
徐伟华,蒋宗颖
(西南大学 人工智能学院,重庆 400715)
0 引 言
直觉模糊集[1]是保加利亚学者Atanassov在1986年提出的一种基于模糊集理论[2]的推广.其核心思想是在模糊集隶属度的基础上,增加了非隶属度以及犹豫度的概念,以期能够更加全面、清晰地描述和理解模糊概念.直觉模糊集理论提出以来,受到了国内外学者的广泛关注,也成功应用到物流服务、图像融合、决策判断、机器学习、医疗诊断等领域[3-7].当前已经成为处理模糊性和不确定性问题的有效工具.
粗糙集[8]是1982年波兰学者Pawlak提出的另一种处理不确定性问题的工具.该理论强调从数据本身出发,不需要任何所研究问题的先验知识便可以从数据中发现知识.属性约简[9-10]是粗糙集理论研究中最为重要的内容之一,其基本内容是指在保持决策能力不变的前提下尽可能去除冗余元素,降低知识库的内存存储空间,有助于在知识获取过程中降低时间复杂度.此外,众多学者从不同的角度对属性约简进行了研究,并取得了很多重要成果[11-14].
现实生活中,决策信息系统一般不是基于等价关系,而是基于条件属性取值为直觉模糊数的优势关系,这更符合实际需求.本文通过对隶属度、非隶属度和犹豫度加权定义了一个加权得分函数,从而定义了一种直觉模糊偏序关系,并在此基础上构造度量偏好直觉模糊序决策信息系统.进一步在度量偏好直觉模糊序决策信息系统中引入了分布(最大分布)函数和分布(最大分布)辨识矩阵,给出获取决策信息系统全部分布(最大分布)约简的方法,并通过一个具体实例分析比较了两种约简方法的优劣性.
1 度量偏好直觉模糊序决策信息系统
信息系统通常由论域和条件属性构成,特别地,当信息系统中具有决策属性的时候,称该信息系统为决策信息系统.为了更好地理解决策信息系统,在此给出相关的基本概念[15-16].

定义2给定一个决策信息系统DI=(U,AT∪{d},F,G),对任意f∈F,g∈G,a∈AT和x∈U,有f(x,a)=(θa(x),ϑa(x)),g(x,d)∈R(R为实数集),分别表示对象x在条件属性a和决策属性d下的取值.其中,函数θa:U×a→[0,1]和ϑa:U×a→[0,1]分别表示U中对象x在条件属性a下的隶属度和非隶属度,并且满足0≤θa(x)+ϑa(x)≤1,称f(x,a)为直觉模糊数.
进一步,记h(a)={(θa(x),ϑa(x))|a∈AT},称h(a)为U上的直觉模糊集.如果满足上述性质,则称IS=(U,AT,F)是直觉模糊信息系统,DI=(U,AT∪{d},F,G)是直觉模糊决策信息系统.
定义3已知DI=(U,AT∪{d},F,G)是直觉模糊决策信息系统,∀x∈U,∀a∈AT,定义对象x对属性a的加权得分函数为:
Sa(x)=ω1θa(x)-ω2ϑa(x)-ω3πa(x)
其中:θa(x)和ϑa(x)分别表示U中对象x在条件属性a下的隶属度和非隶属度,并且始终满足0≤θa(x)+ϑa(x)≤1,πa(x)=1-θa(x)-ϑa(x)表示对象x在条件属性a下的犹豫度,从而加权得分函数可以进一步表示为:
Sa(x)=(ω1+ω3)θa(x)+(ω3-ω2)ϑa(x)-ω3
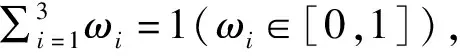
下面将定义直觉模糊决策信息系统中条件属性值和决策属性值的偏序关系.
定义4给定DI=(U,AT∪{d},F,G)是直觉模糊决策信息系统,对于∀f∈F,∀g∈G,∀a∈AT以及∀x,y∈U,有:
h(x,a)≥h(y,a)⟺Sa(x)≥Sa(y)
g(x,d)≥g(y,d)
则称DI=(U,AT∪{d},F,G)为直觉模糊序决策信息系统,记DI≥=(U,AT∪{d},F,G).
根据直觉模糊序决策信息系统的构造,可以得到基于条件属性和决策属性的递增或递减的偏序关系.若某一条件属性下得到的条件属性值域构成了一个递增或递减的偏序关系,则称该条件属性为该直觉模糊决策信息系统的一个准则,同理可以获取相对应的决策准则.根据上述讨论,可以获取由条件属性值域和决策属性值域递增或递减偏序关系构成的优势关系.本文主要讨论由递增的偏序关系获得的优势关系,不失一般性,本文方法在递减的偏序情况下同样适用.

因此,在度量偏好直觉模糊序决策信息系统中,如果a∈AT,∀x,y∈U,x、y之间存在优势关系“≥”,则用“x≥y”表示x在准则a下优于y.


={(x,y)∈U×U|Sa(x)≥Sa(y),∀a∈A}


={y∈U|Sa(y)≥Sa(x),∀a∈A}
2 度量偏好直觉模糊序决策信息系统的分布约简

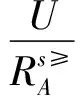
引理1设α=(a1,a2,…,an)T,β=(b1,b2,…,bn)T是两个n维向量,如果ai=bi(i=1,…,n),则称向量α等于向量β,记作α=β;如果ai≤bi(i=1,…,n),则称向量α小于等于向量β,记作α≤β;如果出现其余情况,则称向量α不小于等于向量β,记作α>β.
由引理1和分布函数以及最大分布函数的定义,可以获得在度量偏好直觉模糊序决策信息系统下的相关性质.






(2)~(4)可以由定理2.1(1)和分布函数以及最大分布函数的定义可得.








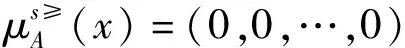
因此,原定理成立.

证明:与定理2.3类似.
3 度量偏好直觉模糊序决策信息系统的分布约简方法
在第2节给出了在度量偏好不协调直觉模糊序决策信息系统下分布(最大分布)函数的定义以及判定定理,这是在准则集下判断分布约简的基础.在本节中,将通过定义分布辨识矩阵的方式给出具体计算分布约简的方法.






因此,原定理成立.



是该度量偏好直觉模糊序决策信息系统的分布辨识公式.


4 案例分析
假设某医院的10位医生对7个病人(x1,x2,x3,x4,x5,x6,x7)进行联合诊断,他们分别对这些病人的病症(a1,a2,a3,a4)做出判断,病症通常为心痛等模糊性词语,医生基于病人描述以及从医经验给出这些病人拥有这些病症的程度,从而判断该病人此刻的病情状况,病情状况分为A、B、C三种.表1给出了10位医生对7个病人的诊断情况,在表1中这样解释病人x1在病症a1下的直觉模糊数:一共有10位医生,有4位医生认为该病人具有病症a1,5位医生认为该病人不具有病症a1,还有1位医生无法给出准确判断.这时,认为病人x1对病症a1的隶属度为0.4,非隶属度为0.5,犹豫度为0.1,记作f(x1,a1)=(0.4,0.5).可以类似地解释其他直觉模糊数.此外,在加权得分函数中,人们往往更看重隶属度,所以在此设置偏好权重为ω1=0.6,ω2=0.3,ω3=0.1.

表1 度量偏好直觉模糊序决策信息系统
为了便于后续计算在该度量偏好直觉模糊序决策信息系统中的分布约简以及最大分布约简,在表2计算了任意对象x∈U对任意属性a∈AT的加权得分函数.
根据表2,可以知道:

表2 上述决策信息系统的加权得分函数

方法1:利用定义6求解分布约简与最大分布约简.
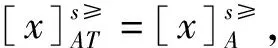
方法 2:利用定理3.2求解分布约简与最大分布约简.
根据表1的度量偏好直觉模糊序决策信息系统,可得该系统下的分布约简辨识矩阵,如表3所示.

表3 上述决策信息系统下的分布辨识矩阵
特别地,便于记录,在表3中,用属性的下标表示属性,用0表示分布可辨识属性集为空集的情况.
由此可得:

(a1∨a4)∧a4(a1∨a3∨a4)∧(a2∨a3∨a4)∧(a3∨a4)∧a3(a2∨a3)∧
(a1∨a2∨a3∨a4)∧(a1∨a2)=a1∧a2∧a3∧a4
因此,{a1,a2,a3,a4}是该度量偏好直觉模糊序决策信息系统的分布约简,由定理2.2可以知道{a1,a2,a3,a4}也是该决策信息系统的最大分布约简.
根据计算出的分布约简以及最大分布约简,可以知道,条件属性集AT是使每个病人在病情决策类中隶属度保持不变的属性集,同时它也是每个病人在最大分布病情决策类中保持不变的属性集.
比较方法1和方法2,发现二者的计算结果都相同,但是它们所需要的时间未必相同,为了更加客观地比较不同方法在计算时间上的优劣,分析了这两种方法在最坏情况下的时间复杂度.为了计算时间复杂度,把任意两个对象在任一属性下关于加权得分函数的一次比较作为一次基本运算,那么在最坏的情况下,可算得方法1的时间复杂度为O(|U|2×|AT|×2|AT|),方法2的时间复杂度为O(|U|2×|AT|).比较最坏情况下不同方法的时间复杂度,认为在保持结果一致的前提下应该采用方法2,即分布辨识矩阵的方法来求解分布约简,因为这能大量减少时间成本.
5 结 论
本文在直觉模糊序决策信息系统中,借助偏好权重定义了加权得分函数,从而构造了度量偏好直觉模糊序决策信息系统.通过研究分布约简的性质得到了相应的判定定理,给出了两种获取分布约简的方法,并通过一个具体的实例验证了两种方法的可行性与有效性.

