含层间水的双层加筋板结构声振传递特性研究
杨智雄,殷学文,吴文伟,王纬波
(中国船舶科学研究中心 船舶振动噪声重点实验室,江苏 无锡 214082)
0 引 言
双层周期加筋板结构通常具有良好的力学性能和抑振隔声性能等多功能特性,已被广泛用作高速机车、飞机以及舰船的壳体结构等。这类结构层间通常存在流体介质,当内板受到激励力振动时,振动波将同时通过加筋板和层间流体的双通道路径传递到外板上,所以探究双板结构的连接介质(加筋板、层间水层等)对双板结构声辐射的影响有着重要的意义。数十年来人们围绕周期性加筋单板/壳结构开展了大量富有成效的工作,为双层周期加筋板结构的振动和声学研究奠定了基础。典型的研究有:Mace[1-2]应用傅里叶积分变换方法,分别对平行分布和正交分布线支承的无限大单板在点力激励下的声辐射问题开展了研究;Burroughs[3-4]将Mace的方法推广到单点激励下双周期加肋无限长单层圆柱壳的远场声辐射中,并用有限长的双周期加肋壳体进行了数值验证;吴文伟等[5-6]进一步地应用傅里叶变换技术,分别给出了等间距相同加强单板以及双层圆柱壳在浸入无限大理想可压流体中的辐射声解析公式,系统评估了各要素对远场辐射声压级的影响;Maxit[7]充分考虑了加强筋的弯曲和扭转运动,从波数空间中结构声振耦合角度考察了周期加筋板在点激励和流体载荷作用下的振动和声辐射特性。针对周期性加筋单板/壳的声辐射问题,近年来的研究重点逐渐从匀质结构转移到复合材料结构上来,其中以Yin等[8--9]、Cao等[10-11]的工作最具代表性。
针对双层板加筋结构,Wang 等[12]基于空间谐波展开法建立了层间平行加筋的双层板传声理论模型,结合频散关系详细分析了传声过程中相关现象的物理机理;在此基础上,Legault和Atalla[13]对典型飞机机身结构的传声损失特性进行了研究,即层芯空腔填充纤维吸声材料的平行加筋双层板结构。Xin 等[14-15]应用傅里叶变换法,建立了二维周期正交加筋三明治夹层板结构声辐射理论模型,考虑了加筋板的拉伸运动、弯曲和扭转运动,同时考虑了加筋板的质量惯性效应。针对有限大结构,通常采用模态分析或数值分析方法。沈承等[16]采用模态函数法研究了对边简支加筋三明治板的隔声特性,通过将板的另一维度作为无限大,将三维结构问题简化为二维问题。最近,张冠军等[17]采用结构有限元/声学自动匹配层直接声振耦合计算方法,以四边简支双层加筋板为对象,研究了双层加筋板结构单面触水下的声场特征。
综上所述,现有公开文献仅考虑了加筋板的单一层间振动传递方式对双板结构传声以及声辐射特性的影响,而同时考虑层间水影响的相关研究未见报道,层间流体声振传递途径、产生条件和影响机理尚不明晰。本文在Xin等[14]的方法基础之上,进一步建立了含层间水的正交加筋双层板结构声辐射理论模型,完善了通过层间连接结构和流体介质的双通道传递路径下的双板结构声振耦合特性研究;模型精确考虑了加筋板的横力、弯矩、扭矩作用以及质量惯性效应,并从考察远场辐射声压频谱和位移波谱的角度,详细讨论了不同激振位置、层间介质以及加筋参数的变化对其声振传递特性的影响,相关结论对该类结构的减振降噪有着重要的意义。
1 理论模型
本文采用的含层间水的正交周期加筋双层板模型如图1所示,双层板单面触水,集中点力作用于上面板,激发结构弯曲波经由层芯加筋板和层间水传递到下面板,经流固耦合作用向半无限大声场中辐射噪声。上下面板的面密度分别为m1和m2,厚度分别为h1和h2,并由两组分别平行于x轴和y轴方向的正交加筋板连接,其间距分别为lx和ly,厚度分别为tx和ty,线质量密度分别为mx和my,高度均为d。简谐激振力q0eiωt作用于上面板坐标为(x0,y0)处,将两面板考虑为Kirchhoff 薄板,加筋板同样考虑为薄板结构,据此建立点力激振下含层间水的正交加筋双层板声辐射理论模型。
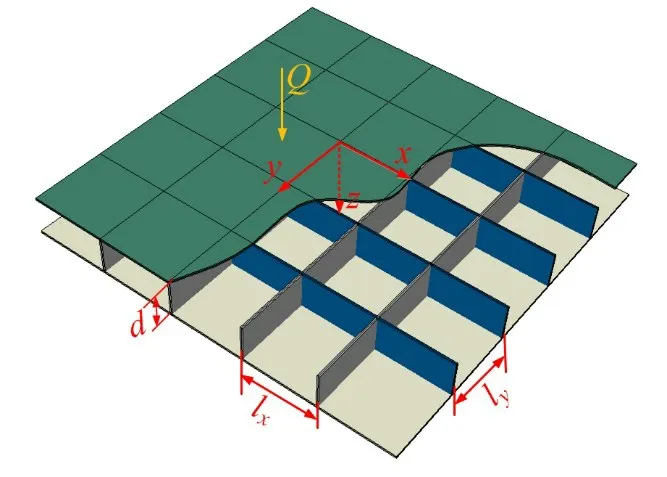
图1 含层间水的正交加筋双层板结构示意图Fig.1 Orthogonally rib-stiffened double-panel structure with inner water
1.1 运动控制方程
上面板除受到集中点力以及层芯加筋板反作用力外,还受到层间流体的声压载荷作用,其振动控制方程为

式中,依赖波数(α,β)的项用符号“~”标记,表示其为相应项的傅里叶变换。
1.2 层间与半无限外场声压载荷
假设层间与半无限场均为理想流体,则层间流场声压p1与外流场声压p2均满足如下波动方程:

式中,k2=ω/c2为外场流体波数,c2为外场介质声速。
1.3 加筋板作用力
加筋板分别作用于上下面板的横力、弯矩和扭矩的表达式参见文献[14],对其进行傅里叶变换,横力的傅里叶变换为
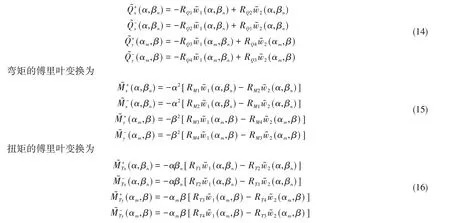

式中,(GxJ*x,GyJ*y)为半个加筋板的扭转刚度,(Jx,Jy)为加筋板的扭转惯矩。各参数表达式详见文献[14]。
1.4 波数域位移
将式(6)~(19)代入式(4)和式(5)可得

将式(20)和式(21)中的(α,β)替换为(α′m,β′n),由此产生两组联立代数方程组:

在保证级数结果收敛的前提下,对上述联立方程组进行截断取值,得到有限大代数方程组(-m̂ 选定球坐标系(r,θ,φ)的原点为激励点(x0,y0),由下面板振动响应位移w͂2(α,β)辐射的远场声压p2(r,θ,φ)为 层间水对双层加筋板声振传递特性的影响机理通过数值分析结果来研究。模型均为钢制材料,其结构阻尼通过复弹性模量E(1+iη)起作用,其中损失因子η=0.002,弹性模量E=210 GPa,密度ρ=7800 kg/m3,泊松比υ=0.3;上下面板厚度h1=h2=15 mm,加筋板厚度tx=ty=10 mm,间距lx=ly=500 mm,高度为d=50 mm;空气密度为1.21 kg/m3,声速为343 m/s,水中密度为1000 kg/m3,声速为1500 m/s;单位简谐点力作用在上面板(lx/2,ly/2)位置;声压场点位于r=100 m,θ=φ=0°。在讨论中,如果没有特殊的说明,这些参数保持不变。 本文采用自行编程进行计算,将理论模型对考虑内外场均为空气时的弱耦合作用下的正交加筋双层板预测结果与Xin 和Lu[14]的结果进行对比,验证本程序的正确性和可靠性。模型的几何参数与材料属性参见文献[14]。 图2~3 分别对应(0,0)、(lx/2,ly/2)激振点处双层加筋板辐射声压级曲线。由图可见,两种激振情况下理论模型的预测结果与文献中的结果符合得很好。有些激振频率下的细微差异主要是由于该理论模型同时考虑了层间和外流场空气与双板的弱耦合作用,而Xin 和Lu[14]的理论模型则没有考虑这一点。当激振点位于板格中心时,空腔与双板之间的弱耦合作用更加强烈,SPL曲线上具有更多的峰谷值。 图2 正交加筋双层板结果对比(lx/2,ly/2)Fig.2 Comparison between present results and those by Xin and Lu[14]for the orthogonally rib-stiffened double-panel structure at location(lx/2,ly/2) 图3 正交加筋双层板结果对比(0,0)Fig.3 Comparison between present results and those by Xin and Lu[14] for the orthogonally rib-stiffened double-panel structure at location(0,0) 当内底板受到激励时其振动波由内底板传递到外部流场中的途径有两种:(1)通过层间流场传递。内底板振动波通过层间流体介质传播到外底板并激励外板,与此同时产生反向波经层间流场向内底板传递,并激励内板振动。这种正向波和反向波产生相互耦合作用,时而抵消时而加强,最后通过外板振动向外场辐射声波;(2)通过加筋板传递。当内板受激振动时,振动波通过加筋板传向外板并激励外板振动,同样外板振动时产生反向激励,通过加筋板返回到内板,相互耦合后再通过外板向外场辐射。由此,本节讨论仅由层间水传递(A模式)、仅由层间加筋传递(B模式)、同时由层间水与加筋板传递(C模式)这三种模式对双层板远场声辐射的影响。 图4 和图5 分别对应(0,0)、(lx/2,ly/2)激振点处,双层板在不同层间振动传递模式下的声压级随频率的变化曲线,此时外流场与下板的耦合作用很小。由图4 可以看出,A 模式下的SPL曲线在4200 Hz附近存在明显的峰值,这与双板空腔结构的耦合共振有关;B模式下,板内弯曲波经由周期加筋板,产生复杂的波数变换和波型叠加效应,并由上板-加筋板-下板强耦合在一起,导致声压级曲线上出现了丰富的峰谷值。此外,由于加筋板与面板的强耦合作用,其传递的振动能量要大于介质水传递的能量,由此产生的远场辐射声压级整体较大,其整个带宽内的声压总级为59.0 dB,高于A 模式下带宽内的声压总级55.9 dB。C模式在2500 Hz以下的中低频范围内的辐射声压总级为41.4 dB,显著低于B模式在同频段的辐射声压总级52.4 dB,这是由于双板与层间水在低频耦合效应较强,其传递的振动波与加筋板传递的振动波存在相位差导致的,整体上表现为抑制了结构振动;在2500~8000 Hz 频段范围,C 模式辐射声压级曲线有大于B 模式的趋势,二者辐射声压总级分别为63.4 dB 和57.9 dB,表明此时层间水与加筋板具有同步促进振动传递的效果。 图4 层间振动传递模式对双层板在空气中辐射声压级影响(lx/2,ly/2)Fig.4 Comparison of SPL in air between three different transmission channels at location(lx/2,ly/2) 图5 层间振动传递模式对双层板在空气中辐射声压级影响(0,0)Fig.5 Comparison of SPL in air between three different transmission channels at location(0,0) 当激振点作用于强筋处时,图5中B、C 模式下声压级曲线各峰值水平较低,计算得到的声压总级分别为43.6 dB 与40.6 dB,与图4 中点力作用于板上的结果相比,辐射声压级显著降低。这是由于加筋板阻抗增大,抑制了双板的振动响应,从而导致了声压级普遍降低。此外,当点力作用在强结构上时,整体上振动能量传递由加筋板主导,尤其在中低频,层间水的传递能量相对较小,因此两种模式下声压级曲线的低频差异较小;随着频率升高,加筋板阻抗逐渐增大,对振动具有抑制作用,层间水的影响相对凸显,从而导致二者声压级曲线在高频有明显的错峰现象。 图6 和图7 分别给出了上述两处典型激振位置下的双板结构在不同振动传递模式下的水下辐射声压级曲线。由于振动波在相邻加筋板与上下面板间的传递、反射以及叠加作用,形成了一系列的驻波共振和驻波衰减,体现为图中B 模式下相比于A 模式,声压级曲线上出现了一系列峰值和谷值,因此远场辐射声压级在某些频段增大,某些频段减小。 图6 层间振动传递模式对双层板的水下辐射声压级影响(lx/2,ly/2)Fig.6 Comparison of SPL in water between three different transmission channels at location(lx/2,ly/2) 图7 层间振动传递模式对双层板的水下辐射声压级影响(0,0)Fig.7 Comparison of SPL in water between three different transmission channels at location(0,0) 从图6 可以看到,当点力作用在面板上时,在中低频B、C 模式下的水下远场辐射声压级数值相当;在高频C 模式曲线数值高于B 模式。这是由于在中低频,外场水与层间水分别与面板的耦合作用相反,外场水对下面板振动有正相激发作用,层间水有反相抑制作用,二者作用相互抵消,导致两种模式的曲线在中低频差异较小;而在高频,二者对振动影响与加筋板作用一致,均有同相促进作用,且相对于仅层间水的单面耦合作用,内外水域的双向耦合作用强烈,更有利于双层板间振动传递至下面板向外辐射噪声。当点力作用在加筋强结构上时,观察图7可看到,整个计算频段内的振动传递主要由加筋板主导,尤其在中低频;在高频,随着加筋板阻抗升高,振动传递减弱,下面板的双面耦合作用相对明显,导致B、C曲线差异变大,这与上述结论一致。综合图4~7,加筋板仍然是双板层间振动传递的主要途径,决定了SPL曲线的总体变化趋势;但加筋板与层间水的双通道振动传递叠加结果与具体分析频段和激振位置有关,还受外场流体介质耦合作用影响。 当激振频率为f=5 kHz的简谐点力作用在(lx/2,ly/2)位置时,下面板在上述三种振动传递模式下的位移波谱云图如图8所示,亮点代表位移幅值较大。从图8(a)可以看到,仅含层间水的双板结构与无限大单层板具有特征相同的位移波谱云图,表明二者的动力学特性相似。其中明亮窄圈半径对应层间水耦合的双板结构的自由行进弯曲波数;暗圈半径为流体波数,暗圈以内对应超音速波,可以向外场辐射声;暗圈以外对应亚音速波,为近场攸逝波。图8(b)显示了正交加筋夹层板的横向位移波谱,可以发现加筋板显著改变了结构的动力学特性,亮点以明亮窄圈为中心向外呈指向性分布,分布范围更广,反映了正交加筋板的波数变换效应,结构辐射声同时与高波数与低波数成分的振动波有关;在此基础上,图8(c)给出了进一步考虑层间水的位移波谱云图,一个显著特征是在可辐射声的暗圈范围内亮点明显增多,可直观解释图6 中双通道模式下的高频声压幅值与另外两种模式相比有了大幅提高的现象。 图8 不同层间振动传递模式下的横向位移波谱云图Fig.8 Transverse displacement spectra under three different transmission models 正交加筋板间距lx、ly以及高度dx、dy作为关键系统参数,其对含层间水的双层板层间振动传递势必有重要影响。图9和10分别显示了上述两种激振位置下加筋板周期间距对含层间水的加筋双层板水下声辐射的影响。 图9 加筋板间距对辐射声压级影响(lx/2,ly/2)Fig.9 Comparison of SPL between different spacing of adjacent stiffeners at location(lx/2,ly/2) 从图9中可以看到,当加筋间距很小时,SPL曲线平滑,没有出现任何波峰和波谷,这与无限大单板结果一致,此时层间水的影响可忽略不计,层间振动传递由加筋板主导,且正交加筋双层板的水下声辐射特性可等效成单层板来计算;当加筋板间距相对于弯曲波波长很大时,相邻加筋板之间的面板可近似于无限大单板,表现为SPL曲线趋势与仅含层间水的双板结构一致,此时加筋板的影响可忽略不计,振动传递由层间水主导;加筋间距适中情况下,加筋板起着类似于振动节点的作用,相邻加筋板之间的板格受点力激发出多种共振模态,整体上不利于结构的减振降噪。当点力作用在强加筋结构上时,观察图10 可发现,不同加筋板间距下SPL曲线变化规律与图9 一致;但间距最大时SPL曲线共振峰向高频偏移,此时加筋板主要增大了结构刚性,而振动主要由层间水方式传递。 图10 加筋板间距对辐射声压级影响(0,0)Fig.10 Comparison of SPL between different spacingof adjacent stiffeners at location(0,0) 本节继续讨论加筋板厚度对含层间水的双层板振动传递特性的影响,图11和12分别对应板格中心激励和加筋强结构处激励下的SPL曲线。观察两图可以发现,不同厚度下的SPL幅值在中低频的差异要明显小于高频范围。该现象表明加筋板与面板的耦合作用随频率的升高而增加,加筋板的厚度变化引起相应的刚度变化,并在高频时随着耦合作用增强,强烈影响着振动传递特性,造成SPL幅值差异变大。所不同的是,由上述分析可知,当点力作用在面板上时,在中高频,层间振动传递由加筋板与层间水双通道同相叠加,厚度最小时的刚度最弱,能量传递较小,因此,从图11 中观察到对应的辐射声压级最低;而当点力作用在强结构上时,振动传递主要由加筋板主导,且加筋板阻抗随频率和刚度增加而升高,因此图12 中加筋板厚度越大对应的辐射声压级越小。另外,加筋板厚度与刚度直接相关,最终影响到共振峰的疏密分布。加筋板越厚对应刚性越大,共振模态分布越稀疏,导致SPL曲线上峰值点越少。 图11 加筋板厚度对辐射声压级影响(lx/2,ly/2)Fig.11 Comparison of SPL between different thicknesses of stiffeners at location(lx/2,ly/2) 图12 加筋板厚度对辐射声压级影响(0,0)Fig.12 Comparison of SPL between different thicknesses of stiffeners at location(0,0) 本文建立了含层间水的双层加筋板结构远场声辐射理论模型,首先通过算例对比验证了方法的准确性;系统阐述了层间水作用下的双板结构振动传递特性机理;并以含层间水的加筋双板结构为例,数值分析了加筋参数对两种振动传递通道下的远场声辐射特性影响,得出了以下结论: (1)点力作用在面板上时,层间水也是重要的声振传递通道。内外水耦合作用在低频对振声传递具有反相抵消效果,在中高频具有同相叠加效果,此时双通道模式大幅增强了能量传递,导致远场辐射声压级增大,位移波谱云图也直观反映了这一点。 (2)点力作用在强筋结构上时,声振传递特性主要由加筋板主导,其阻抗随频率的升高而增大,在高频能量传递受到抑制,层间水与结构耦合影响相对明显。 (3)加筋板参数对含层间水的双板结构声振传递特性有重要影响。间距增大,振动传递由加筋板主导转为层间水主导,与激振位置无关;而厚度的影响与激振位置有关,作用在面板上时,由于中高频的双通道振动传递的同相叠加作用,厚度越大响应越高;作用在强结构上时,由于阻抗抑制作用,厚度越大响应越低。1.5 远场声辐射

2 数值结果与讨论
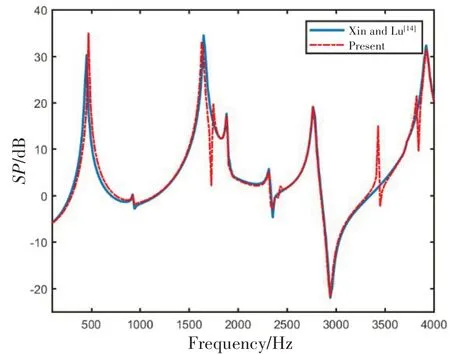
2.1 计算程序验证

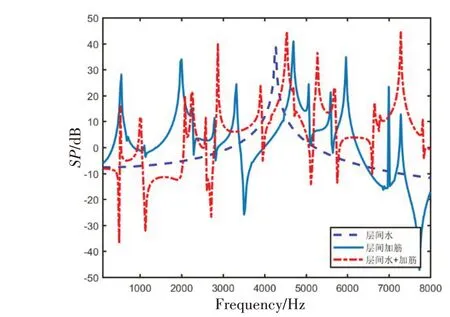
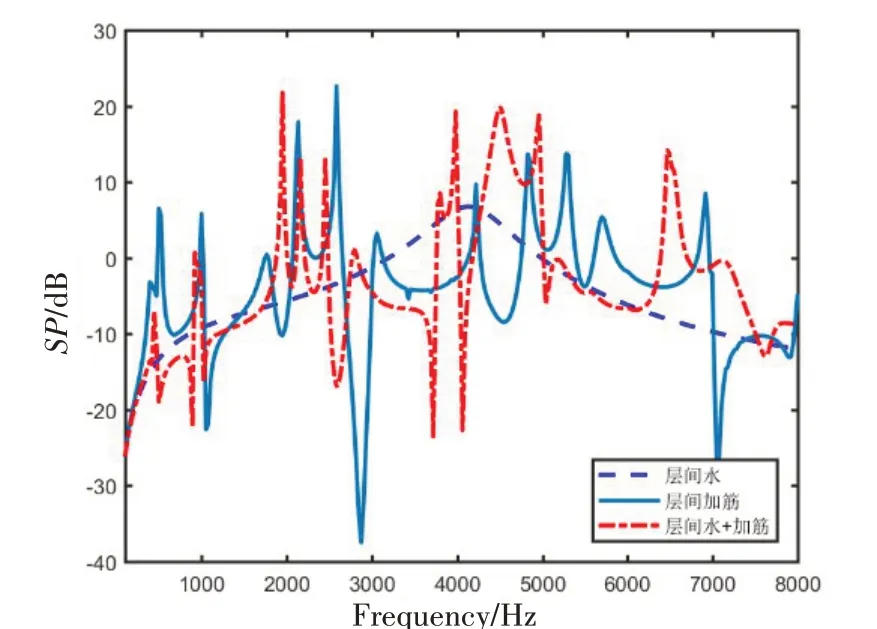
2.2 层间水对振动传递特性的影响



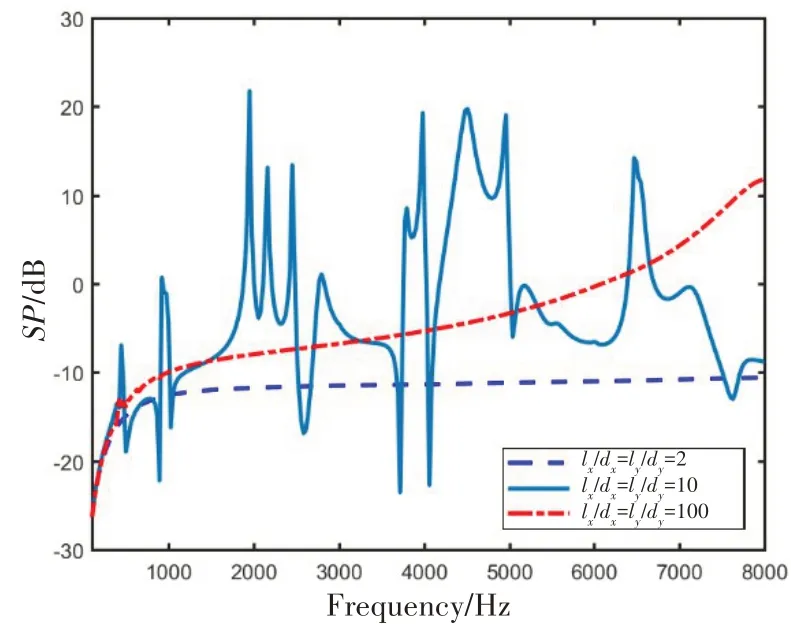
2.3 筋板间距对含层间水的振动传递特性影响

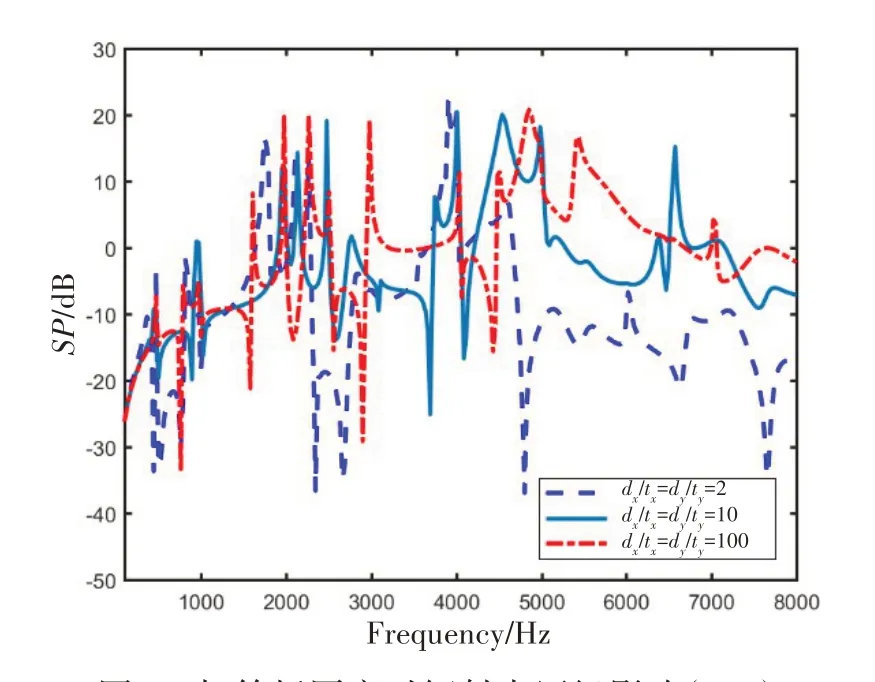
2.4 筋板厚度对含层间水的振动传递特性影响

3 结 论

