泛场景自适应优化的多输出最小二乘SVR光谱反射率重建方法

樊煜，王慧琴，王可，王展，甄刚

（1 西安建筑科技大学信息与控制工程学院，西安710055）

（2 陕西省文物保护研究院，西安710075）

0 引言

光谱反射率被认为是物体的“指纹信息”，能够反应物体颜色的本质属性。获取到物体的光谱反射率信息即可准确还原物体在不同光照条件下的真实颜色［1-3］，在出版印刷［4］、壁画颜料识别［5］、纺织［6］等场景中有着重要应用。基于多光谱成像的光谱反射率重建技术因其非接触、高效、使用场景多样化等优点近年来被广泛使用，其过程可看作利用各成像设备输出的低维多通道响应值信号重建被摄物体的高维光谱反射率信息［7-9］。

目前常用的光谱反射率重建算法有伪逆法［10］、维纳估计法［11］、回归模型重建法［12］等。其中，伪逆法及维纳估计法虽计算简单，但对数据采集的物理环境要求较高，易受系统噪声影响，泛化性能差。在回归模型重建法中，ZHANG W F 等［13］研究表明，在小样本集上支持向量回归（Support Vector Regression，SVR）的重建精度及泛化性能均优于维纳估计法和传统伪逆法，但标准SVR 是一维的，忽略了各输出之间潜在的交叉相关性。针对此问题，DEGER F 等［14］提出基于多输出支持向量回归（Multiple Output Support Vector Regression，MSVR）的光谱反射率重建方法。通过将SVR 的损失函数定义在超球体上，实现模型的输出为某一样本在连续多通道下的光谱反射率，增强了各输出分量相关性，一定程度上提高了抗噪性能及重建精度，但其凸二次规划问题计算复杂，导致模型收敛速度慢。总体来说，MSVR 的模型适用性更具优势，更适用于光谱反射率重建。但在实际应用中，由于多光谱成像系统受到不同环境特别是光源的影响，重建模型性能存在差异。模型的参数设置直接决定模型的重建效果，不同重建场景下模型的最优参数也不尽相同。上述各方法虽在特定场景中的重建精度不断提高，但重建模型在多场景下的参数最优化问题尚未解决，适应性有所欠缺，无法达到泛场景下的光谱重建最优效果。

针对泛场景下光谱重建模型的参数最优化问题，本文提出一种自适应优化的多输出最小二乘SVR（Multiple output Least Squares SVR，MLS-SVR）［15］光谱反射率重建方法。在使用MLS-SVR 作为光谱重建模型的基础上，融合光谱曲线拟合精度和变化趋势，提出一种带有自适应权重的模型综合评价指标，并以此为适应度函数使用混沌麻雀搜索算法（Sparrow Search Algorithm，SSA）［16］对模型参数动态寻优，提高模型在多种场景下的泛化性能。最后使用最优参数的MLS-SVR 模型进行光谱反射率重建，并与伪逆法、MVSR 法、MLS-SVR 法进行对比实验，评价并讨论实验结果。

1 光谱成像系统及光谱重建模型

多光谱成像系统和光谱重建算法的种类有很多，为确保光谱重建应用的场景广泛性，采用结构较为简易的单色CCD 相机与带通滤光片的组合作为多光谱成像系统［17］，使用具有良好泛化性能及模型适应性的MLS-SVR 作为光谱重建模型。

1.1 多光谱成像系统

与普通成像系统相比，多光谱成像系统最本质的特点为可获取多个通道下的图像［18］，采用单色CCD 相机与带通滤光片组合作为一个多光谱相机，其单个样本在第i个通道的响应值可用积分描述为

式中，Uv为某个样本在第v个滤波片下的相机响应值，r(λ)表示在波长λ处的光谱反射率，E(λ)表示相机所在光源的光谱功率密度，gv(λ)为第v个滤波片下相机的光谱灵敏度函数，Bv为第v个滤波片下的暗电流响应，ev为第v个滤波片下的图像噪声。若多光谱相机有n个通道，物体的光谱反射率采样点个数为N，则式（1）可用向量矩阵表示为

式中，U为n×1 的相机响应值向量，R为N×1 的光谱反射率向量，G为n×N的光谱响应矩阵，B和e皆为n×1 的系统噪声向量。若忽略系统的图像噪声e，同时通过标准白板校正其暗电流噪声B，则可将式（2）表示为

式中，M为转换矩阵，通过式（3）可将多光谱成像模型简化为一个相机响应值与光谱反射率之间的回归模型。

1.2 MLS-SVR光谱反射率重建模型

2 MLS-SVR 参数自适应优化光谱重建算法

MLS-SVR 建模过程中需要确定三个参数，分别为核参数p、正则化参数η和γ。参数值的选取决定了模型的学习能力及泛化性能，直接影响光谱重建效果。可以利用智能优化算法对模型进行参数寻优。然而多光谱成像系统采集环境的差异导致不同重建场景下模型的最佳参数并不相同，因此构造合适的适应度函数是寻优的前提条件［19-21］。常用的适应度函数为静态模型精度评价指标，无法动态获取不同重建场景下模型的最优参数，并且单一评价指标只能评价模型的拟合精度，无法兼顾模型输出的变化趋势。由于光谱反射率重建本质上属于数据拟合，模型预测输出的光谱反射率曲线趋势与拟合精度同样重要［22-23］。因此提出一种融合模型拟合精度与变化趋势且带有自适应权重的综合评价指标，将该评价指标作为适应度函数使用SSA 对模型参数进行寻优。

2.1 模型综合评价指标

光谱重建精度的评价可等价为对回归模型拟合精度的评价，平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）是一种常用的模型精度评价指标，表示预测值与真实值的平均偏离，MMAPE∈[0，+∞)的值越小表明模型拟合精度越高。其公式为

式中，N为波段数，R(λ)为真实光谱反射率，为重建光谱反射率。

Pearson 相关系数通常用来衡量模型预测输出与真实值的变化趋势，用ρ值表示，|ρ| →1 表示预测值与真实值的相关性很强，|ρ| →0 表示两者相关性很弱，其公式为

为了达到兼顾模型重建的精度与变化趋势，适应更广泛的光谱反射率重建场景，结合上述两种评价指标，提出一种如式（12）所示的模型综合评价指标。

式中，k1为自适应权重，默认取值为0.5，最小取值间隔为0.1。同时F作为麻雀搜索算法优化重建模型的适应度函数，决定了重建模型的优化目标，即兼顾重建后的拟合精度及变化趋势。为了适应各重建场景下不同的建模需求，可通过改变权重k1的取值主导模型优化目标的偏好，即模型的优化方向侧重于重建后的拟合精度或变化趋势。

2.2 基于混沌SSA 的MLS-SVR 参数优化

麻雀搜索算法（SSA）是一种依托于麻雀觅食与反捕食机制的新型群智能优化算法，具有收敛速度快、参数设置少、搜索精度高等特点，其寻优效果强于粒子群算法、灰狼优化算法等其他群智能优化算法。通过模拟麻雀的觅食过程进行迭代寻优，同时加入预警机制，每只麻雀的位置等同于一个解。麻雀在觅食时有着明确的分工，可分为发现者、跟随者和警戒者三种不同角色，通过不断更新各麻雀位置最终获得最佳适应度值和全局最优值，完成MLS-SVR 的参数寻优过程。

但使用SSA 对模型参数进行优化时，其种群随机初始化易导致求解优化问题时陷入局部最优。因此参考文献［24］引入Chebyshev 映射，用其混沌性代替种群的随机初始化，保证初始种群在搜索空间分布的均匀性。Chebyshev 映射方程为

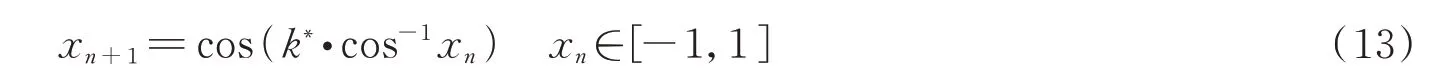
式中，xn为映射变量，k*为映射阶数，当k*＞2 时，系统处于混沌状态。

针对基于混沌SSA 的MLS-SVR 参数对(p，η，γ)的优化，使用式（12）模型综合评价值作为其适应度函数。具体优化步骤为：

Step1 参数初始化。对种群数量，发现者、警戒者比例，警戒值，最大迭代次数进行初始化，适应度函数权重，参数对取值范围等进行初始化。

Step2 利用式（13）对麻雀种群进行混沌初始化。

Step3 计算初始种群各麻雀适应度，排序选出当前最优、最差值及其对应位置。

Step4 将适应度值优度靠前的部分麻雀作为发现者，其余部分视为跟随者，同时进行位置更新。

Step5 在麻雀种群中随机选取部分麻雀作为警戒者，并更新其位置。

Step6 进行迭代，获取每次迭代的适应度最优值，若当前最优值好于上次迭代最优值则执行更新操作，否则不执行更新。

Step7 判断是否达到求解精度或最大迭代次数，若是，执行下一步，否则跳转至Step3。

Step8 停止循环，输出全局最优值和最佳适应度值。

2.3 算法结构

基于MLS-SVR 参数自适应优化的光谱重建算法结构如图1所示，首先挑选训练样本，使用多光谱成像系统和光纤光谱仪分别获取所选样本的相机响应值及光谱反射率数据，对其进行归一化处理。然后选择合适核函数并使用试凑法确定自适应权重k1，其过程为以0.1 为间隔对k1在［0，1］范围内进行逐个取值，对比k1每次取值后模型重建的平均光谱均方根误差（RMSE）大小，取平均光谱RMSE 最小值时的k1为符合该重建场景下建模要求的最佳权重。确定自适应函数后使用混沌SSA 对模型参数进行迭代寻优。最后使用最优参数的MLS-SVR 对输入的相机响应值测试样本进行光谱反射率重建，并对重建结果进行评价。

图1 MLS-SVR 参数自适应优化的光谱重建算法结构示意图Fig.1 Structure diagram of MLS-SVR parameters adaptive optimization spectral reconstruction algorithm

3 实验与结果分析

3.1 实验环境及数据准备

为了验证所提方法的有效性和普适性，使用Ocean Optics 公司的单色CCD 相机和10 个不同波峰（波峰分别为420 nm、475 nm、540 nm、580 nm、620 nm、660 nm、680 nm、715 nm、740 nm、780 nm）的窄带滤光片组成多光谱成像系统，在CIE 标准照明体D65 光源下进行数据采集，为无环境干扰的暗室实验室理想采集环境，其中多光谱成像系统滤光片的带宽为20 nm。实验中，将213 张标准德国劳尔（RAL）色卡作为实验数据，通过多光谱成像系统采集10 个波段通道的RAL 色卡光谱数据，同时利用Ocean Optics SpectroSuite QE6500 型科研级光纤光谱仪获取其波长在380～780 nm 的光谱反射率，采样间隔为10 nm。

训练样本的选取应避免数据冗余的同时具有代表性。根据光谱误差最小原则，同时使用Mohammadi法、Fvector 法及Hardeberg 法建立训练样本个数与其重建后均方根误差平均值的关系［25］，如图2所示。

由图2 可知，随着样本数增多，三种样本选取方法的光谱误差皆呈下降趋势，样本个数为40～50 时下降幅度最大，在样本个数大于50 后平均光谱RMSE 无显著改善。综合来看，三种方法在选取训练样本个数为50 时效果最佳，即确定训练样本个数为50。

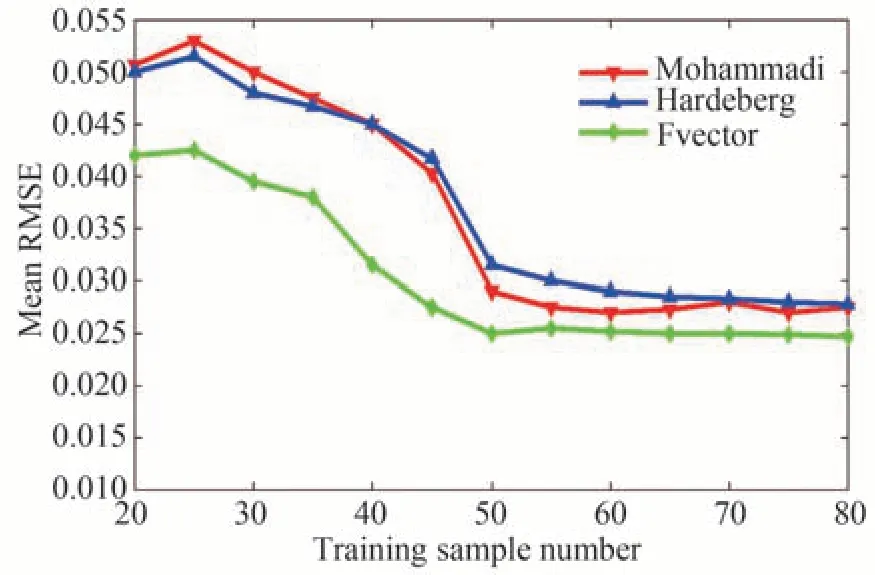
图2 训练样本数量与平均光谱误差关系Fig.2 The relationship between the number of training samples and the average spectral error

3.2 评价标准

目前对于光谱重建效果并无固定的评价标准，本文综合均方根误差（MRMSE）、适应度系数（MGFC）及色差（ΔE）三种主流方法作为重建精度的评价标准。

1）均方根误差MRMSE

MRMSE用来评价光谱真实值与预测值之间的拟合误差，其值越小表明重建精度越高。

2）适应度系数MGFC

MGFC用来测量光谱反射率真实值与预测值的余弦夹角，其值范围为0～100%。当MGFC值大于99.5%时，表示重建效果可以接受，当MGFC值大于等于99.9%时，表示重建效果非常优秀。

3）色差ΔE

在CIELAB 空间中两种不同颜色的差异可以用其欧式距离表示。若在CIELAB 空间中两种颜色的坐标分别为和，则两者色差ΔE可表示为

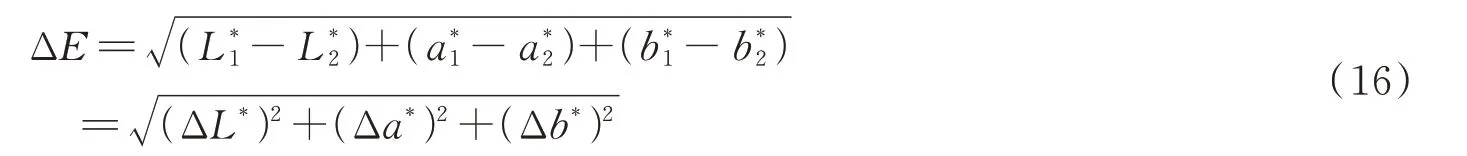
式中，ΔL*表示明度差，Δa*表示红绿色品差，Δb*表示黄蓝色品差。

3.3 参数设置

模型训练样本为优选的50 个RAL 色卡，另随机选取20 个RAL 色卡作为测试样本。进行SSA 优化时根据经验值［26］设置种群规模为30，最大迭代次数为200，发现者、侦查者比例均为种群总数的20%。根据文献［14］待优化参数对(p，η，γ)的上下限分别为[2-15，23]，[2-10，210]和[2-15，2-5]。由于色卡重建实验的光谱数据采集环境为无外界干扰的理想采集环境，无需对重建模型进行特异性优化，故无需在此重建环境下对k1使用试凑法进行取值，即适应度函数中自适应权重k1取默认值0.5，使优化后的重建模型兼顾拟合精度与变化趋势。最终经过迭代寻优获得最优参数对(p，η，γ)的值分别为0.023 7、0.010 2 和0.74。

3.4 结果分析与比较

在确定模型各参数和训练样本后，分别采用伪逆法、MSVR 法、MLS-SVR 法及本文所提方法对随机选取的20 个RAL 色卡测试样本进行光谱反射率重建，其评价结果如表1所示。

由表1 得，与伪逆法相比，本文方法的平均MRMSE降低了0.006 8，平均MGFC提高了1.91%，平均光谱色差降低了2.494。与MSVR 法相比，本文方法的平均MRMSE降低了0.105 5，平均MGFC提高了0.09%，平均光谱色差降低了0.666。与MLS-SVR 法相比，本文方法的平均MRMSE降低了0.002 8，平均MGFC提高了0.08%，平均光谱色差降低了0.522。

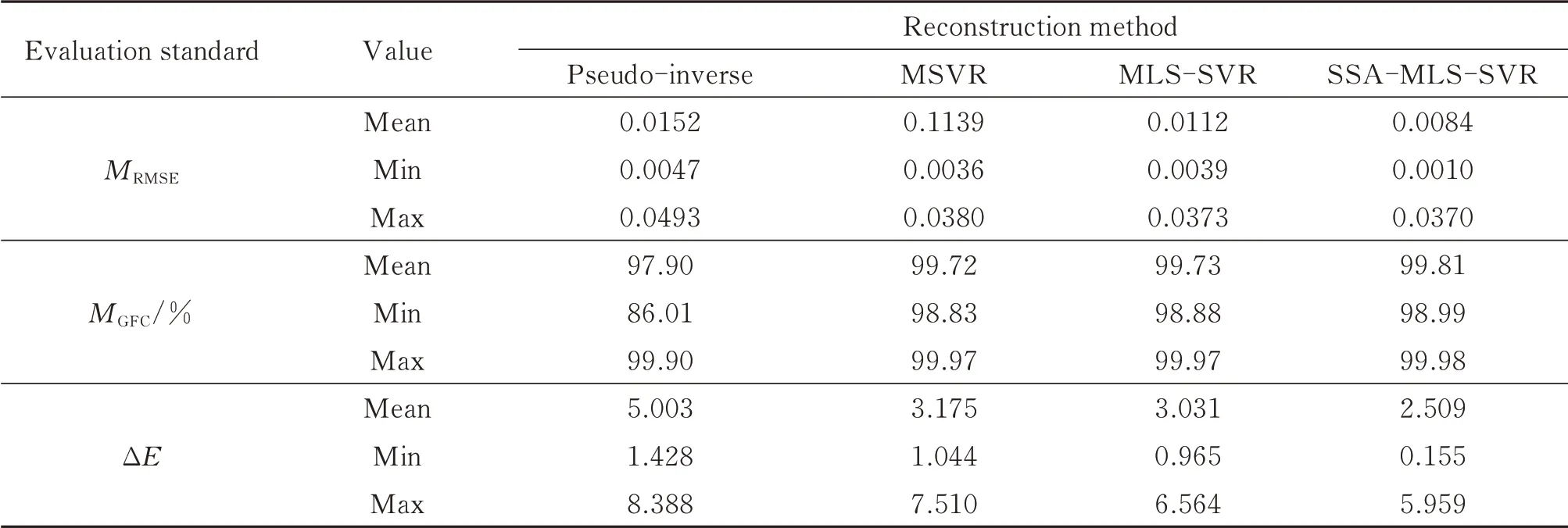
表1 四种光谱重建方法精度比较Table 1 Accuracy comparison of four spectral reconstruction methods

图3 为对20 个测试样本使用四种重建方法的均方根误差对比。四种重建方法的效果各有差异，但总体来看，使用本文方法重建每个样本后的均方根误差皆为最小。MSVR 和MLS-SVR 两者的均方根误差较为接近但都差于本文方法，伪逆法的重建精度最低。

图3 测试样本均方根误差对比Fig.3 Comparative test sample RMSE

从RAL 色卡中随机选取第2 001 色块、3 012 色块、5 019 色块及5 026 色块作为测试样本，使用四种方法进行重建测试，其真实光谱与重建光谱对比如图4所示。可知，与伪逆法、MSVR 法和MLS-SVR 法相比，使用本文方法对色卡重建后，光谱反射率曲线与真实光谱曲线拟合程度最好。

图4 四种重建方法的光谱反射率曲线Fig.4 Spectral reflectance curves of four reconstruction methods

3.5 应用验证

为了验证本文方法在实际不同场景中的重建效果，选取某寺庙内殿堂壁画及古代彩绘文物上共5 处不同颜色区域，分别使用上述四种方法进行重建并评价。光谱数据采集环境为寺庙殿堂内，受自然光影响导致光照条件复杂。重建色块标记处如图5所示。

图5 壁画及彩绘文物色块标记Fig.5 Color block markers for murals and painted cultural relics

在实验数据采集中，光纤光谱仪的工作区域为孔径8 mm 的积分球中心圆形探口，多光谱成像系统则是对整个采集对象的二维平面区域进行光谱数据采集，最终呈现在分辨率大小为1 408×1 040 的图像中。图6为光纤光谱仪及多光谱成像系统的工作方式示意图。

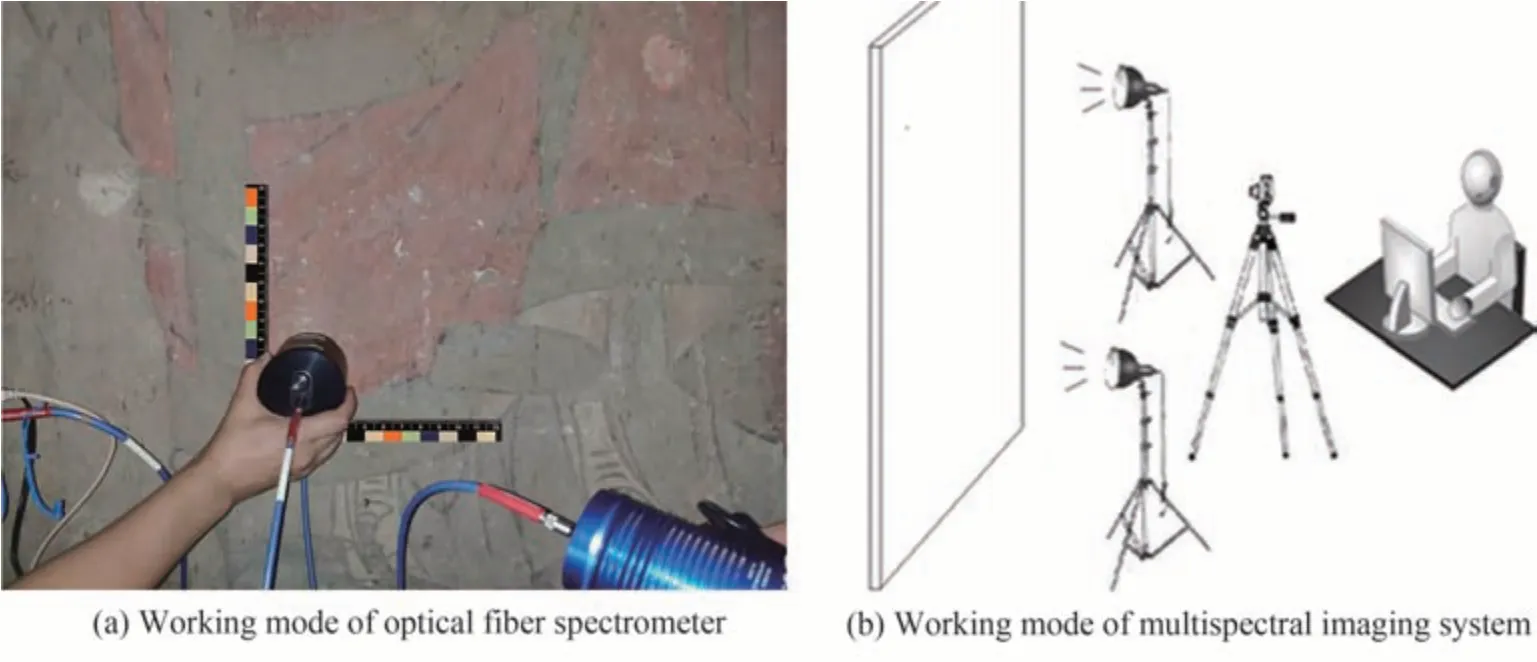
图6 光纤光谱仪及多光谱成像系统的工作方式示意图Fig.6 Schematic diagram of working mode of optical fiber spectrometer and multispectral imaging system

在进行光谱数据提取时，为了最大化避免因颜料涂抹不均造成的误差，使用光纤光谱仪选择颜料分布均匀且纯净的区域中心进行光谱数据采集，同时使用标尺对其工作位置进行严格记录，最后与多光谱成像系统成像后的图像通过标尺进行目标采集区域的定位与匹配，计算其对应区域内像素的平均相机响应值，并使之与光纤光谱仪所测光谱数据相对应。具体过程如图7所示。通过标尺严格记录了光纤光谱仪的工作区域，其中灰色区域表示直径为D的积分球工作区域，中心黑色区域表示直径为d的光纤光谱仪采集的目标区域。在光纤光谱仪采集完成后保留标尺位置，随后使用CCD 相机采集多通道图像，最后根据标尺位置可计算出多光谱图像中相机响应值的取值区域大小，并根据区域内的像素数量求得目标采集区域的平均相机响应值。具体方法为，根据标尺位置可知相机响应值采集区域是以标尺起始测量位置为相对原点，以(D/2，D/2)处为圆心、以d/2 为半径的圆形区域。通过ENVI 软件处理多光谱图片，获取该区域内像素点数量和各像素相机响应值。考虑到CCD 相机所拍画面中标记区域内所占像素点数量由CCD 相机与被摄目标的距离决定，通过实验已获得在距离为1 m、2 m 和3 m 处目标采集区域内的像素点数量分别为75、21 和12。实验拍摄距离为2 m，光纤光谱仪探口孔径d为8 mm，积分球直径D为8.5 cm、即可求得CCD 相机采集目标区域的平均相机响应值，同时保障了相机响应值与光纤光谱仪所测光谱数据的区域相对应。

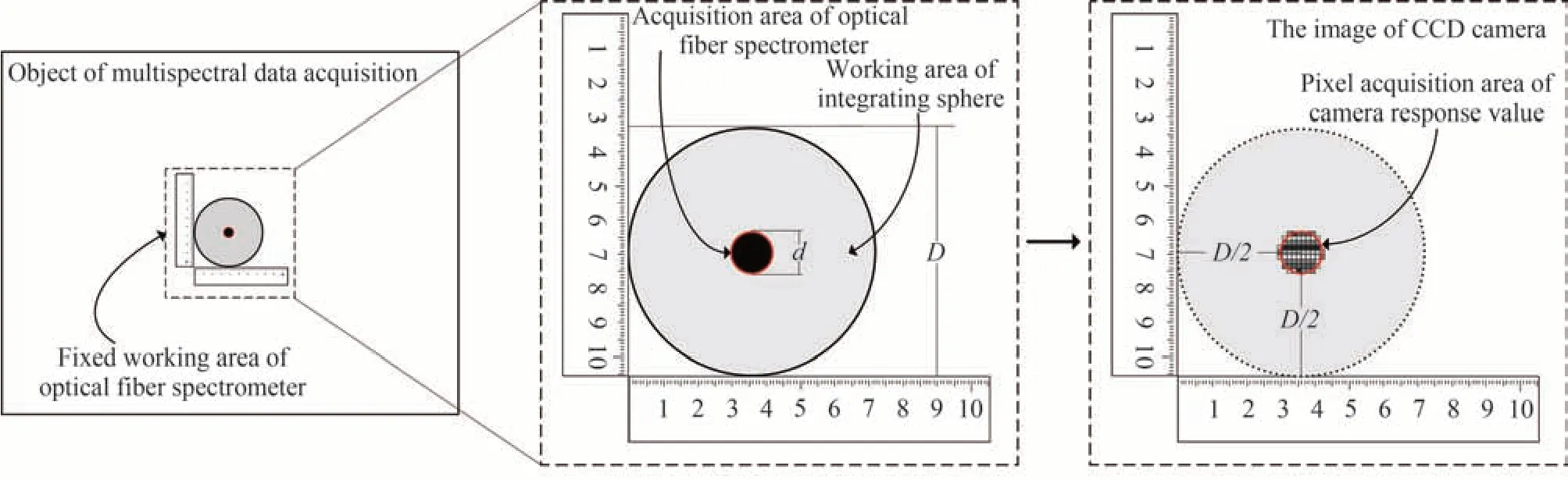
图7 光纤光谱仪与多光谱成像系统采集区域对应示意图Fig.7 Schematic diagram of corresponding acquisition area between optical fiber spectrometer and multispectral imaging system

为保障实验中多光谱成像系统采集时的目标成像均匀性，首先确保目标对象表面光照的均匀性，在拍摄场景中两个标准D65 光源均与目标成45°，确保表面受光照均匀。其次通过CCD 相机及三脚架上所置水平仪确保其处于水平工作位置，采用电脑控制的电子快门保证在其工作时静止不动，调节焦距使被测对象保持在CCD 相机取景画面中央，同时保持拍摄距离、曝光时间、光圈大小和感光度不变。最后还需通过拍摄标准均匀灰板校正所拍样本数字图像的光照不均匀性。

在上述操作基础上，使用光纤光谱仪测量各标记处的真实光谱反射率数据，再使用多光谱成像系统采集各标记处10 个通道的相机响应值，将两者作为测试样本，使用本文方法进行重建。重建过程示意图如图8所示。采集10 个波段的多光谱图片，对其相机响应值进行归一化处理，选择要重建的像素区域输入到训练好的SSA-MLS-SVR 光谱重建模型中，模型输出则为高维光谱反射率值。其中，λ表示光谱波段，n为波段采集总数，各波段图像大小为PX×PY，N为重建得到的光谱反射率波段数。

图8 光谱重建流程示意图Fig.8 Flow chart of spectral reconstruction

由于光谱重建的本质是通过训练样本建立相机响应值与光谱反射率之间的转换矩阵，训练样本的物质及色彩特征可直接影响转换矩阵的构成，故选择合适的训练样本对光谱重建效果有重要意义。由于RAL 色卡为工业颜料制作，而古代壁画颜料主要为矿物颜料［27］，为了能更好地适应古代壁画的特定重建环境，在已有213 个RAL 色卡样本的基础上加入古代壁画常用的矿物颜料及其混合颜料样本50 种，主要为古代壁画红、黄、绿、蓝、白、黑六大色系常用矿物颜料，如银朱、铬黄、石绿、石青、白蛤、炭黑等，以及各颜料与不同比例明胶和其他颜料混合后进行平均涂抹制成的矿物颜料色卡。组成新的训练样本共263 个，并根据上文所提三种样本选取方法对训练样本进行优选，确定最优训练样本个数为65。训练样本个数与光谱均方根误差的关系如图9所示。

图9 混合训练样本数量与平均光谱误差关系Fig.9 Relationship between the number of mixed training samples and the average spectral error

使用本文方法进行重建时，模型重建的精度和趋势偏好取决于其自适应权重k1的取值大小。对于上述重建环境，其光谱数据采集环境光照条件复杂，会受到不同光源的干扰。文献［28］指出，在多光谱成像系统的工作环境中若受到其他光源的干扰，会降低光谱重建的精度。故在该重建场景中，对模型的优化目标应侧重于重建后的拟合精度，遂使用试凑法确定该重建场景下的最佳权重，观察k1取值与平均光谱误差的关系，确定最佳k1值。如图10 可知，在k1为0.7 时平均光谱误差最小，因此设置自适应权重k1为0.7 并建立重建模型。

图10 自适应权重k1与平均光谱误差关系Fig.10 Relationship between adaptive weight k1 and average spectral error

在确定训练样本和模型参数后，分别使用伪逆法、MSVR 法、MLS-SVR 法及本文方法进行光谱反射率重建，重建效果评价如表2所示。可知，与其他三种重建方法相比，使用本文方法对参考色块进行重建的平均均方根误差及色差皆为最小，适应度系数有明显提升。

表2 5 个参考色块的光谱反射率重建评价Table 2 Spectral reflectance reconstruction evaluation of 5 reference color blocks

图11 为5 处壁画及彩绘文物参考色块的光谱反射率真实测量值与使用SSA-MLS-SVR 方法进行重建后光谱反射率曲线对比。可知，使用SSA-MLS-SVR 法对参考色卡进行光谱重建，其重建光谱反射率曲线可较好地与实际测量的光谱反射率曲线重合。

图11 参考色块重建光谱曲线与实际光谱曲线对比Fig.11 Comparison of reconstructed spectral curve and real spectral curve of reference color block

为了能更好地展现使用伪逆法、MSVR 法、MLS-SVR 法及本文方法对参考色块进行光谱重建后的色度精度，将各方法重建的光谱数据转换到CIELAB 空间中，观察各L*、a*、b*分量值分布状况，如图12所示。可知，在CIELAB 空间中，使用SSA-MLS-SVR 法进行光谱重建后的L*、a*、b*值空间分布与实际测量值的距离最短，说明其重建后的色度精度最高。

图12 各重建方法对参考色块重建后的CIELAB 的色度分布空间Fig.12 The chromaticity distribution space of CIELAB reconstructed from reference color block by each reconstruction method

为了进一步直观感受其重建色差，将实际测量的光谱反射率及各重建方法重建后的光谱反射率转换为D65 光源下的sRGB 色彩空间进行颜色复原，观察各色块在四种重建方法下的视觉色差，如表3所示。可知，使用SSA-MLS-SVR 法进行重建后的参考色块颜色与原始色块颜色最为相近，MSVR 法和MLS-SVR法效果较为接近但不及本文所提方法，伪逆法效果最差。说明本文提出的SSA-MLS-SVR 方法在该特定光谱重建环境中能够达到彩绘壁画颜色复原的要求。

表3 各重建方法对参考色块重建后的颜色复原对比Table 3 Comparison of color restoration of reference color blocks reconstructed by different reconstruction methods

4 结论

本文提出了一种自适应优化的多输出最小二乘SVR光谱反射率重建方法。使用MLS-SVR 模型作为多光谱重建的回归模型，提高了模型的收敛速度和小样本拟合精度；融合平均绝对百分比误差和Pearson 相关系数的同时加入自适应权重，构建了兼顾精度与变化趋势的模型综合评价指标作为适应度函数，然后利用混沌麻雀搜索算法进行模型参数寻优。针对不同光谱重建环境，通过试凑法确定自适权重值，建立该环境下的最佳重建模型，达到光谱最优重建效果。实验结果表明，使用本文方法对RAL 色卡进行光谱重建的精度均优于伪逆法、MSVR 法及MLS-SVR 法。在应用验证中，本文方法能够根据特定重建环境自适应调整模型参数，具有更好的泛化性能，对实验参考色块的光谱重建精度及颜色的复原效果优于其他方法，能够满足彩绘文物颜色的高精度复原，具有一定的实际应用价值。