费马小定理的Python简单验证

王德贵

我们在往期利用Python验证过费马大定理，这是数学史上关于数论的经典问题，其实费马小定理也一样享誉数学界，它是初等数论四大定理之一。

今天我们就用Python来简单地验证费马小定理。

在1636年提出的费马小定理是数论中的一个重要定理。它是初等数论四大定理之一：威尔逊定理、欧拉定理（数论中的欧拉定理）、中国剩余定理（又称孙子定理）、费马小定理。在初等数论中有着非常广泛和重要的应用。实际上，它是欧拉定理的一个特殊情况。

费马小定理可以简述为：

如果p是一个质数，而整数a不是p的倍数，则有a的（p-1）次幂除以p余1。

数学表达式为：

假如p是质数，且（a，p）=1，那么 a^（p-1） ≡1（mod p）

还有另一种写法：

假如p是质数，a为整数，那么 a^p ≡a（mod p）

此处三横线为恒等号。有关费马小定理的相关知识这里不做介绍，有兴趣的朋友可以自己去学习，费马小定理已经被证明，今天我们只做简单验证。

我看到这个定理内容，就想到了勾股数，想用Python验证勾股数的方法，来验证费马小定理。

如果想了解更深入的知识，大家可以参考相关资料。今天我们利用Python只做简单的验证。

验证的范围越大，幂次越高，时间复杂度会几何级数增大，大家可以自行测试。

程序设计不是很难，是等级考试二级内容，而自定义函数是四级内容。

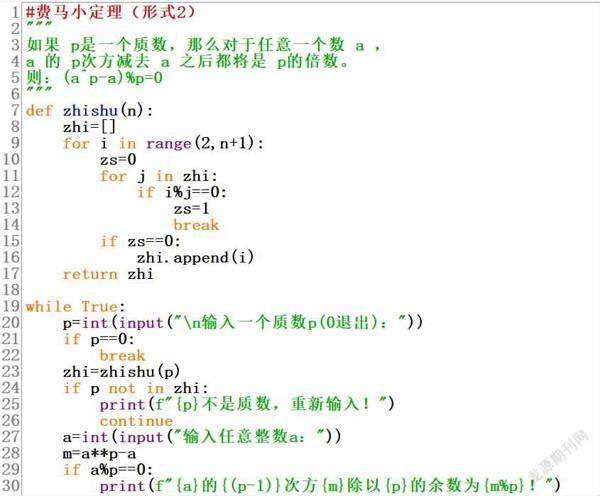
首先生成p范围内的质数列表，并判断p是否为质数。如果不是质数，则重新输入，如果是质数，则提示输入a，如果a与p互质，则提示费马小定理成立，运行结果如下。

如果a是p的倍数，则余数为0，即可以整除p，这个比较好理解。

运行结果：

费马小定理的另一种形式，我们也来验证一下，程序设计如下。基本思路还是先生成p范围内的所有质数列表，然后判断p是否为质数。

如果p不是质数，重新输入p值。如果p是质数，则提示输入任意整数a，然后进行验证，计算并输出结果。

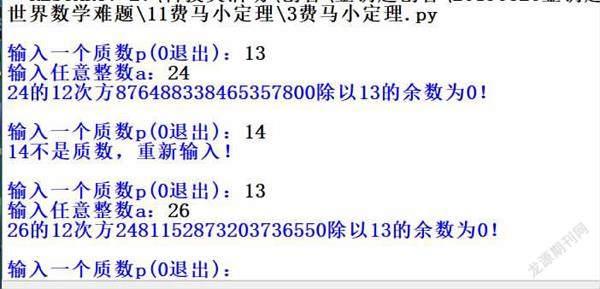
定理的验证测试，多输入几个值，就可以了。也可以在一定范围内验证。

比如，输入一个质数p，让a在一定范围内验证即可。程序如下。

输入p为质数，再提示输入a的最小值和最大值，然后进行逐一验证，并输出结果。

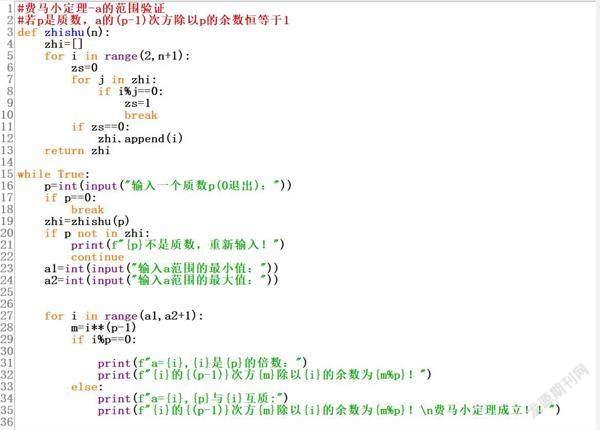
在输入范围30-40时，依次验证，a与p互质时，费马小定理均成立，而当a=34时，a是p的倍数，余数为0。

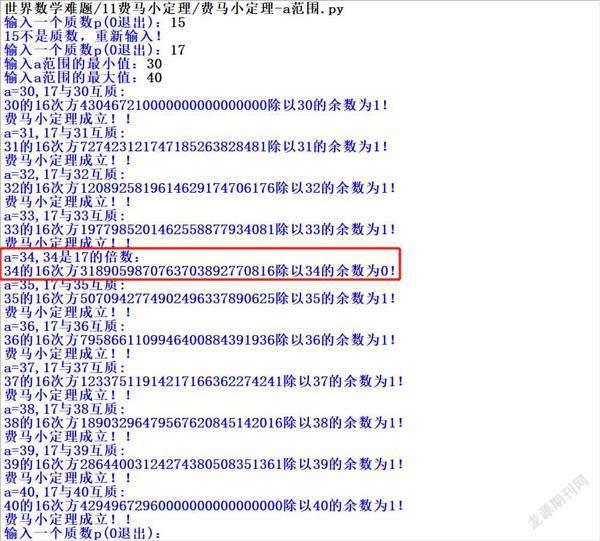
費马在提出定理时，还说明了a是一个素数的要求，但是这个要求实际上是不必要的。

从费马小定理还引申了很多相关数论问题，有兴趣的同学可以参考相关资料，本文不做介绍。如有不当之处，请各位同仁、朋友斧正。