考虑驾驶策略的高速列车运行图节能优化方法*

革 新 张玉召

（兰州交通大学交通运输学院 兰州 730070）

0 引 言

近年来，节能时刻表的研究得到了国内外学者的广泛关注。在降低牵引能耗的研究中，麻存瑞等[1-2]、柏赟等[3]从多方面研究了列车区间节能驾驶策略，陈志杰等[4]研究了在给定站间运行时分前提下的城市轨道交通追踪列车节能操纵优化问题，邓连波等[5]研究了在给定运行时分下基于多速度参数调控的列车运行节能优化策略问题，冉新晨等[6]同时考虑了客流引起的列车质量变化进而影响列车能耗的问题，马阳阳等[7]通过优化列车运行方式有效的降低了列车运营能耗，樊葱等[8]提出了列车多阶段最优控制模型以最小化列车牵引能耗，邓连波等[9]用B样条拟合方法提高了运行时分-最优能耗值的拟合精度和速度；在降低净牵引能耗方面，邓连波等[10]、Su等[11]、陆源源等[12]从降低牵引能耗和增加再生制动能利用率2个角度出发，构建了节能时刻表模型，保证时刻表的净牵引能耗最低；另外，还有将节能问题与其它目标协同优化的研究，如YIN 等[13]、CHEN 等[14]、XIE等[15]、LI 等[16]、张桐等[17]从列车能耗、乘客等待时间、列车运行时间等多目标优化问题出发，协同优化了列车时刻表。

此外，通过区间运行时分的合理分配也可以达到降低牵引能耗的目的，金波等[18]构建了列车运行能耗和区间运行时分分配同步优化的非线性连续节能优化模型，并且使用Cplex求解。盛昭等[19]以区间运行时分和牵引能耗为计算目标建立了驾驶策略优化模型，求解出了能耗-时间的最优解集，采用最小二乘法将二者进行线性化拟合，以此为基础提出了在满足列车始发-终到总运行时间的条件下，通过重新调整每个站间的运行时分，最大化地降低了列车的牵引能耗。

金波等[18]、盛昭等[19]均是通过每列车逐个分配的方法分别获取最优区间运行时分组合，考虑到我国高铁线路1 d内列车发行对数较多，为了保证求解效率，有必要对多列车区间运行时分展开同步分配的研究。

以上重新分配区间运行时分的节能方法仅适用于高铁列车，不适用于地铁列车，其原因主要是地铁列车操纵策略较为简单，区间运行时分较短，可分配的空间并不充裕，除此之外，地铁与高铁列车运行图的编制还存在一定的区别：①列车停站方案不尽相同；②高速铁路往往采用多种速度等级混合运行的组织模式。这些会使得高速铁路列车运行图会涉及到越行及多种时间间隔问题，从而使得其编制更为复杂。

综上所述，本文以高铁列车为研究对象，构建了牵引能耗最小化的多列车区间运行时分同步分配的节能时刻表模型；使用拉格朗日松弛算法求解以保证求解效率；通过宝兰高速铁路对模型及方法的有效性进行验证。

1 构建E-T方程

1.1 计算理论

高铁列车在始发站至终点站的运行过程中，以列车的经停站为断点可划分为多个驾驶区间，每个驾驶区间内列车的操纵策略包括4 个阶段，分别为牵引、巡航、惰行、制动，牵引阶段是列车的提速阶段，纵向受到的力有牵引力、运行阻力，巡航阶段保持恒定的速度运行，所受到的牵引力与运行阻力持平，惰行阶段列车仅在外部运行阻力的作用下滑行，速度缓慢降低，制动阶段列车在制动力与运行阻力的共同作用下减速，列车区间运行的速度距离曲线见图1。

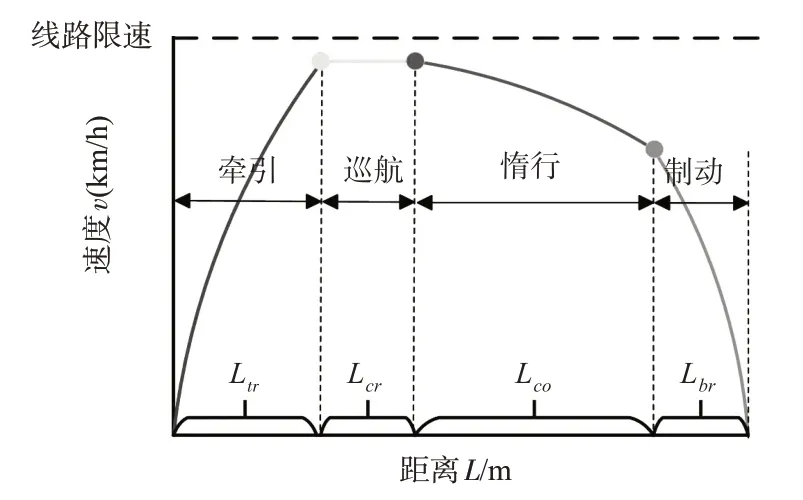
图1 速度-距离曲线Fig.1 Speed-distance curve

将驾驶区间长度划分为多个极小的等距离区间，列车在小区间内的运行可看做匀加速运动，以此为基础构造列车运动学方程，可以描述出列车速度距离曲线，见式（1）。

式中：Δs为距离步长，取1 m；γ为回转系数，取0.06[20]；n和n-1为第n个和第n-1个距离步长；an为第n个距离步长的加速度，m/s2；vn为第n个距离步长的末速度，m/s；tn为第n个距离步长列车的运行时间，s；Fn,合为第n个距离步长下的列车纵向受到的合力，kN。

1.2 构建E-T方程

由图1可见：当牵引距离与巡航距离确定后，通过正推惰行曲线和反推制动曲线寻找二者的交点，惰行距离和制动距离也可随之确定。因此，以牵引距离Ltr和巡航距离Lcr为变化因子，以驾驶区间内的牵引能耗Ei,j和总运行时分Ti,j为计算目标，可以构建驾驶策略集，记为

式（2）和式（3）分别为牵引能耗和区间运行时分的计算公式，其中F(v)为牵引力，根据动车组牵引特性曲线确定。

驾驶策略集里最优解定义为：在可行空间Ω 内，若对于任意的驾驶策略l*∈Ω ，不存在l∈Ω ，使得和同时成立，则驾驶策略l*为最优解。将最优解对应的和拟合成光滑曲线，如图2所示，记为E-T曲线，拟合成的方程式记为E-T 方程，见式（4），如此便可求解出驾驶区间内的牵引能耗与总运行时分的线性关系。

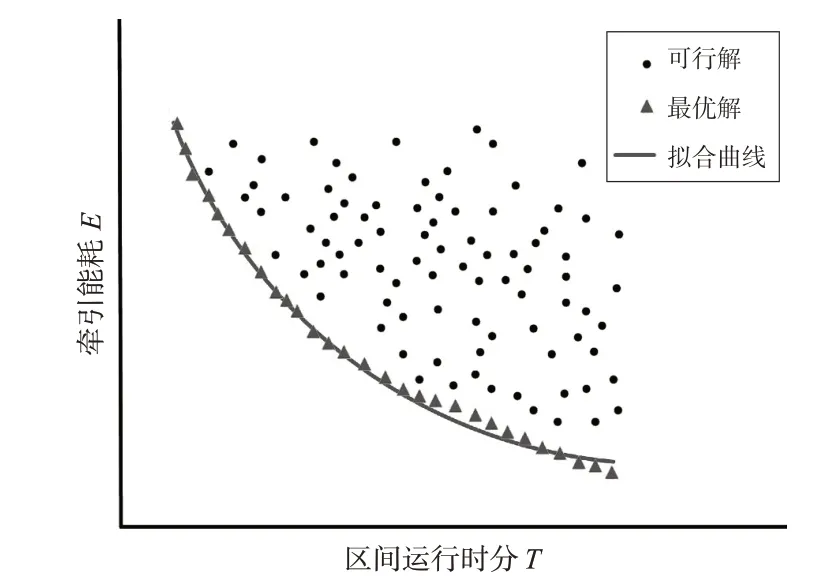
图2 牵引能耗-区间运行时分曲线拟合Fig.2 Curve fitting of traction energy-interval running time

2 模型构建

2.1 问题描述

由1.2节中可知，最优驾驶策略l*所对应的牵引能耗E(l*)与区间运行时分T(l*)的关系可以拟合成光滑的曲线。由于高速列车在多区间运行时各区间坡度、曲线半径、隧道长度等线路条件不同，故不同区间的E-T 曲线也不同，以图3 为例，运行区间a与运行区间b分别表示1列高速列车在不同运行区间的E-T 曲线，对其同时减小等量的运行时分Δt时，牵引能耗的增加量不同，明显ΔEa＞ΔEb。因此，列车在满足全程多区间总运行时分的条件下，各区间运行时分存在最优组合，可以使列车的牵引能耗最低。

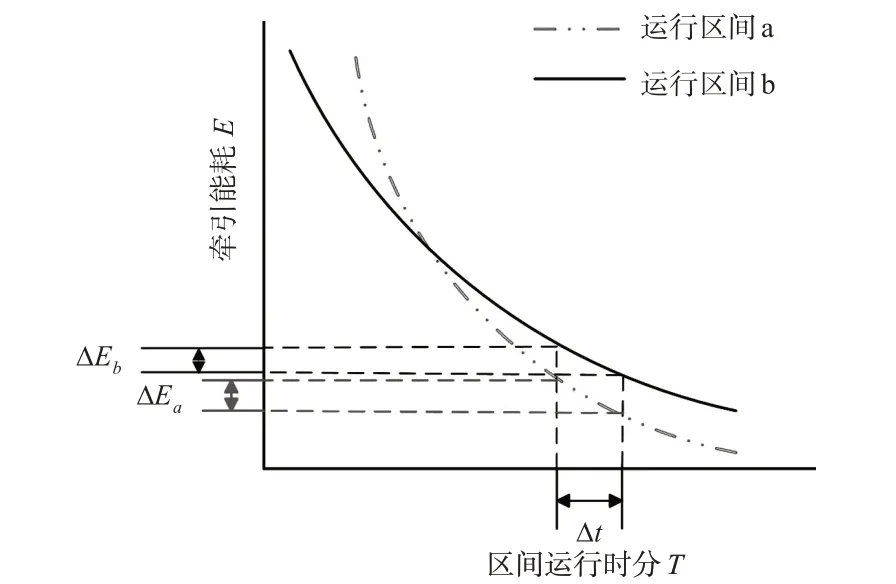
图3 不同区间E-T 曲线Fig.3 E-T curves of different interval

基于此，以区间运行时分、首站发车间隔、经停站停站时间为决策变量，在满足多列车全程多区间总运行时分约束、决策变量取值约束以及运行图安全约束的条件下，重新寻找每列车区间运行时分以及驾驶策略的最优组合，最大化降低时刻表的牵引能耗。本文的研究基于以下2条假设。

1）构造列车运动学方程时，将列车看做单一质点。

2）忽略牵引能耗-区间运行时分的离散点线性化拟合时的误差影响。

2.2 参变量界定

定义集合及索引：K，k分别为列车集合及索引；S，s分别表示车站集合及索引；Uk，uk分别为列车k的发车站集合及索引；Vk，vk分别为列车k的到达站集合及索引；Pk，pk分别为列车k的通过站集合及索引；Nk，(uk,vk)分别为列车k的运行区间集合与索引。

定义参数：Euk,vk为列车k在运行区间(uk,vk)上消耗的牵引能耗，kW·h；Auk,vk，Buk,vk，Cuk,vk为列车k在运行区间(uk,vk)上牵引能耗的拟合参数；α(vk)为列车k到达vk站的时间；β(uk)为列车k离开uk站的时间；γ(pk)为列车k通过pk站的时间；分别为列车k在运行区间(uk,vk)的最小和最大运行时分；Ts,min为车站s的最小停站时间；为车站s的最小追踪间隔；T(k)为列车k的全程多区间总运行时分为车站s的最小到发间隔；为车站s的最小发到间隔；为车站s的最小到通间隔；为车站s的最小通发间隔；m(Nk)为列车k的运行区间数。

定义变量：tuk,vk表示列车k在区间(uk,vk)的运行时分；表示列车k在s站的停站时间；hk,k+1表示列车k与列车k+1在首站的发车间隔.

以上所涉及时间的单位均为秒。

2.3 基本模型

2.3.1 优化目标

该模型的优化目标为所有列车在连续站间运行时牵引能耗最小。

2.3.2 约束条件

式（6）为多列车全程多区间总运行时分约束，相比于单列车全程多区间总运行时分约束而言，该约束从单一向量上升到矩阵层面，因此其复杂度更高。

当列车严格按照时刻表运行时，T(k)即为分配方案给定的总运行时分，在实际情况中为了应对发生早、晚点情况以调整列车区间运行时分的需要，应对各运行区间分配一定的冗余时分，此时T(k)=T(k)+σ，σ表示需要分配的总冗余时分。

式（7）～（9）为决策变量取值约束，其中式（7）为区间运行时分约束，其最大和最小区间运行时分从最优驾驶策略集里确定；式（8）为停站时间约束，一般情况下最小停站时间根据乘客上下车时间以及列车开关门时间确定；式（9）保证了列车在首站满足最小发车间隔，最小发车间隔根据同一闭塞分区只有1 列车运行的原则确定。

若列车满足正点率要求的前提下运行，需要满足一定的运行图安全间隔时间要求，具体见式（10）～（17）。其中k'为在车站vk紧随列车k其后发车、到达或通过的列车。式（10）为相邻2 列车在同一车站的发车间隔约束，式（11）相邻2列车到达同一车站时的到达间隔约束，式（12）为相邻2列车在同一车站，其中前车停站，后车不越行通过时的追踪间隔约束，式（13）为相邻2列车在同一车站，前车不越行通过，后车停站时的追踪间隔约束，式（14）为相邻2 列车不同时到发间隔约束，式（15）为相邻2 列车不同时发到间隔约束，式（16）～（17）为越行列车的到通间隔约束和通发间隔约束。其中约束条件（12）～（13）与约束条件（16）～（17）是互斥的，取决于列车是否越行。

3 算法设计

式（6）是1个矩阵数量级的复杂约束，该约束随着问题规模的扩大(即随着列车数量和运行区间数的增加)将会非常庞大，对问题的求解造成一定难度，参考既有的求解方法，无论使用KKT 条件或是Cplex求解器均不能保证求解效率，因此如何在保证求解精度不降低的情况下，实现多列车区间运行时分同步分配的目标，从而提升求解效率，这对铁路运输生产效率具有重要意义，也是本文研究的重点。

拉格朗日松弛算法的核心思想是针对造成问题难以求解的复杂约束，通过添加拉格朗日乘子将它吸收到目标函数当中，从而减小问题的规模，加快求解速度，因此，本文设计拉格朗日松弛算法求解。下面分别从生成最优解、构造可行解、算法流程3个方面进行详细阐述。

3.1 生成最优解

通过添加拉格朗日乘子λ将式（6）吸收到目标函数后为

s.t：式（7）～（17）

将松弛后的目标函数整理为

拉格朗日松弛算法计算过程中λk是根据上一次迭代确定的已知值，因此ELR的大小与tuk,vk有关，E'对tuk,vk求导得

分析式（22），当λk=0 时，E' 单调递减，故当λk＞0 时，E' 存 在 极 小 点，为：，此时如果该极小点在区 间 内 ， 则tuk,vk=，本文区间运行时分定义的精度为1 s，因此tuk,vk四舍五入取整；如果极小点在区间右侧，通过以上方法，可求解出所有列车的区间运行时分，将该解称为最优解。

3.2 构造可行解

由于将复杂约束条件吸收到了目标函数当中，故松弛问题求解的是原问题的下界(ELR≤E)，因此松弛问题的解有可能不满足约束条件(6)，所以要以松弛问题的解为基础构造原问题的可行解，并求出对应的目标函数作为上界.

如果满足约束条件（6），则该列车的区间运行时分最优组合即为可行解，不做调整；如果不满足约束条件（6），由于拉格朗日乘子λk随着迭代次数增加而逐渐增加，通过3.1 节的分析可知，最优区间运行时分将会从最大值逐渐减小，因此在计算过程中只可能是超出了T( )k的约束，需要将区间运行时分进行压缩处理。使用的方法是使溢出约束条件（6）的运行时分整除m(Nk)，平均分为m(Nk)个等份，在满足区间运行时分最小值约束的条件下对每个运行区间平均压缩，剩余部分以增加牵引能耗最低为原则合理压缩到沿途各运行区间，具体的计算流程如下。

步骤1。判断当前列车是否满足约束条件（6），如果满足，输出可行解；如果不满足，转步骤2。

步骤2。令

判断zk是否等于0，若是，转步骤4；否则，转步骤3。

步 骤3。若，令； 若， 令，循环执行步骤3m(Nk)次。

步骤4。判断列车的各个区间运行时分减小1 s时牵引能耗增加量的大小，在满足的前提下使牵引能耗增加量最小的区间的运行时分减小1 s，其它区间保持不变，循环yk次，输出可行解。

根据上述步骤，遍历完所有列车，即可得出满足总分配时间的可行区间运行时分最优组合，将该解称为可行解。以本文所建模型为例，拉格朗日松弛算法构造可行解的核心思想是牵引能耗增加量最小的前提下寻找满足约束条件（6）的区间运行时分最优组合，但本节仅是对区间运行时分做简单的压缩处理，并未直接考虑牵引能耗的增加量，这是因为随着迭代次数的增加，λk逐渐增加，tuk,vk将会逐渐减小，即溢出约束条件（6）的值会逐渐减小，也就是说迭代到后期，最优解越来越接近可行解，zk将会是0。因此本节设计的寻找区间运行时分可行解的方法无不合理之处，且能提高每一次迭代过程中寻找可行解的速度。

3.3 拉格朗日松弛算法流程

步骤1。输入各区间E-T曲线的线性表达式、各列车全程多区间总运行时分、决策变量最值约束以及运行图安全约束等相关数据。

步骤2。初始化迭代次数j=0，拉格朗日乘子步长参数θ(j)=0.25，第j次迭代后的最小上界UB=+∞，第j次迭代后的最大下界LB=-∞。

步骤3。按照3.1节的方法计算拉格朗日松弛问

题的最优解，并且计算所对应的最优值，如果，则令

步骤4。按照3.2 节的方法构造原问题的可行解，并且求出对应的目标函数值E(j)，如果E(j)＜UB，则令UB=E(j)。

步骤5。判断当前循环是否满足以下任一条件：①迭代次数超过预先设定的值J；②次梯度向量s(j)的模长；③对偶间隙；④步长参数

若符合判断标准转步骤7，否则转步骤6。

步骤6。按照次梯度优化方法更新拉格朗日乘子和步长参数。

步骤7。输出各列车最优可行区间运行时分组合。

最后在满足式（8）～（9）约束的条件下，以式（10）～（17）为安全依据编制运行图，以保证列车的安全运行。

4 算例分析

4.1 算例背景及参数设置

以宝兰高速铁路为例进行算例验证，线路全长400.644 km，沿途共设有8 个车站，设计速度为250 km/h。本文使用10列不同停站信息的CRH3动车组列车编制运行图，动车组参数见表1。

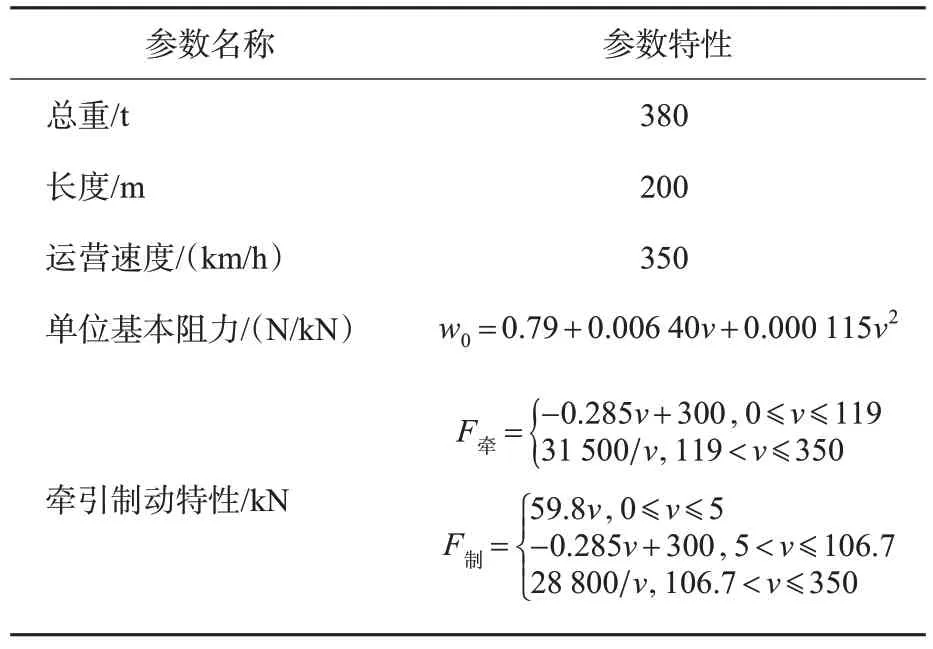
表1 CRH3 动车组参数Table 1 Parameters of CRH3 EMU

此外，令180s(vk∈Vk,k∈K)，图4以榆中站-通渭站为例说明使用oringin软件中Belehradek模型的快速拟合效果，可以看出拟合曲线收敛。值得说明的是，给定线路运行动车组类型、各种间隔时间可能与实际情况不符，但并不影响算例的测试。

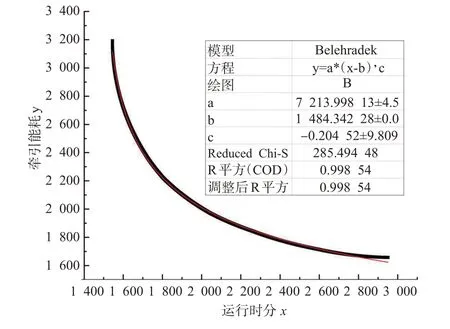
图4 榆中-通渭的E-T拟合曲线Fig.4 Fitting curve renderings

4.2 算例求解

用Python 编写并运行程序，得出图5（a）所示的拉格朗日松弛算法的计算过程。由图5 可见：随着迭代次数的增加，目标函数值的上界逐渐减小，下界逐渐增加，二者逐渐逼近，对应的最优可行解也越来越接近精确解，迭代74次就已经求解出最优的分配结果，计算时间为10 s，实现了多列车区间运行时分的同步分配，最终的次梯度向量为在该算例背景下，上界变化范围较小，图8（b）为纵坐标刻度尺放大后上界的变化情况。

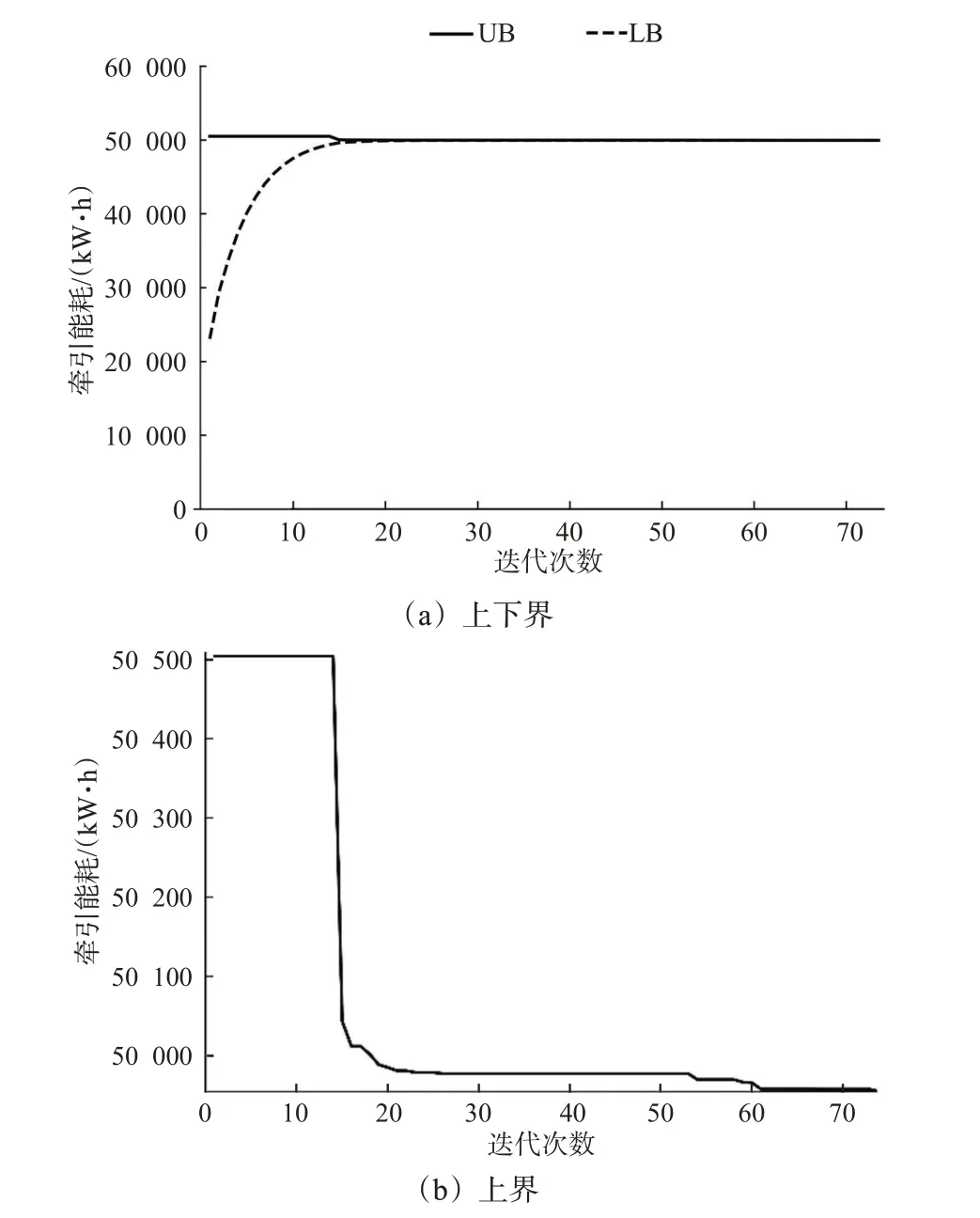
图5 拉格朗日松弛算法计算过程Fig.5 The calculation process of the Lagrangian relaxation algorithm

4.3 结果分析

4.3.1 节能效果分析

表2所示为优化前和优化后的列车牵引能耗比较，可以看出，在保证全程多区间总运行时分不变的条件下，通过对每列车区间运行时分的重新分配，各列车均达到了节能的效果，10 列车的节能率在0.83%～1.24%之间不等，总共节约了595.958 kW·h的牵引能耗，总体的节能率达到了1.2%。图6 所示为优化前后列车在各运行区间的能耗对比，通过重新分配后各区间的能耗有增有减，同一型号动车组列车在不同停站方案下各区间的能耗增减量不同，但就整个连续站间而言能耗降低量大于增加量，总体的牵引能耗均呈现下降的特征，如车次8，9，10，优化前分别在兰州西站—定西北站、定西北站—天水南站、天水南站—宝鸡南站的牵引能耗为1 105.464，3 221.738，1 105.286 kW·h，优化后分别为1 117.899，3 179.419，1 116.298 kW·h，总体的能耗下降量为45.09 kW·h，其它车次均有此种特征，此外，不同型号动车组列车在相同停站方案下其能耗的增减量也不同，这是由于动车组牵引制动特性曲线不同，从而使构造出的E-T 方程不同所导致的。

图6 优化前后运行区间能耗比较Fig.6 Comparison of energy consumption between operating stations before and after optimization

表2 节能效果Table 2 Energy saving effect

4.3.2 时刻表分析

表3为优化前后列车发到时刻的比较，图7为优化前后列车运行图的比较。由表3和图7可见：各车次的平均偏离时间与原有时刻表相比而言其调整的幅度和范围极小，均在2 min 以内，除了对原有时刻表的影响较小之外，可以预见后续对动车组使用计划制定的影响较小，整体而言，对铁路运输的整个生产过程产生的波动性很低。

图7 优化前后运行图Fig.7 Timetables before and after optimization

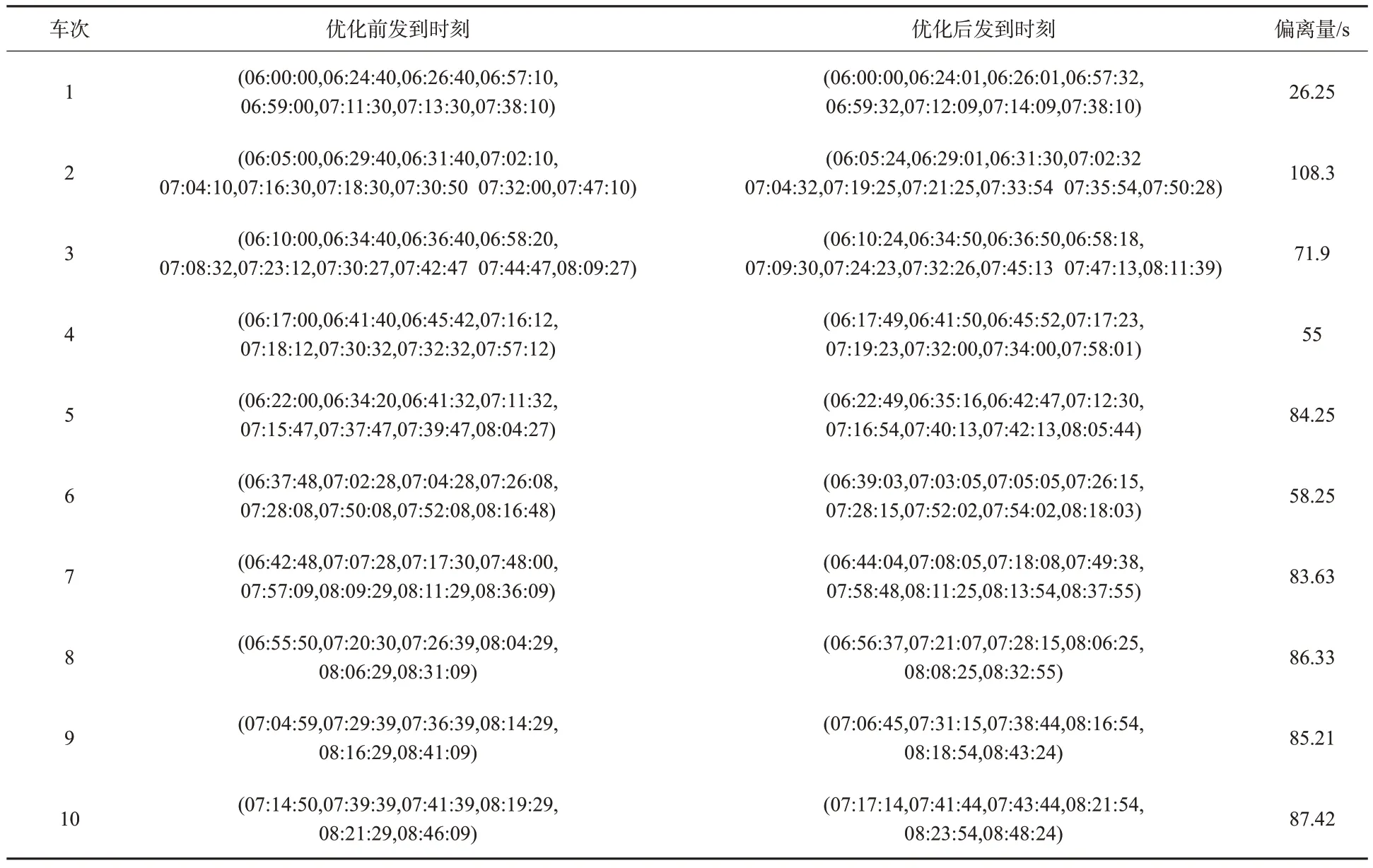
表3 优化前后发到时刻比较Table 3 Comparison of depart and arrive time before and after optimization

综上，本文提出的考虑驾驶策略的时刻表节能优化方法不仅在保证求解精度不降低的条件下，提高了求解效率，实现了多列车区间运行时分同步分配，而且对原运输计划的影响较小，具有实用性较强的优点。

5 结束语

1）本文首先通过调整工况转换点的位置建立了高速列车区间运行最优驾驶策略集，将最优驾驶策略对应的牵引能耗与区间运行时分的离散关系进行线性化拟合，基于此构建了区间运行时分最优分配的节能时刻表模型，并使用拉格朗日松弛算法求解，实现了多列车区间运行时分同步分配的目标。

2）以宝兰高速铁路为背景进行实例验证，通过与优化前的运行图相比较，总共节约了595.958 kW·h 的牵引能耗，节能率达到了1.2%，且本文提出的考虑驾驶策略的时刻表节能优化方法计算速度快、对运行图的影响小，具有较强的现实意义。

笔者仅仅考虑了以牵引能耗最低为目标的区间运行时分的最优分配方案，并未考虑列车再生制动能利用率随操纵工况的调整、停站时间以及发车间隔的调整是动态变化的，因此，在本文研究的基础上最大化再生制动能利用率是以后的研究重点。