人机混驾交通流交织区换道模型切换控制策略*

李 霞 李明烨 张孝铭 崔洪军 马新卫

（1. 河北工业大学土木与交通学院 天津 300401；2. 帝国理工大学商学院 伦敦 SW72AZ）

0 引 言

在人机混驾交通流下，交织区车辆的换道行为因换道压力、自动驾驶车辆信息交流的存在而与一般换道行为存在差异[1]，且自动驾驶车辆换道行为可在一定程度上实现主动控制，故可对人机混驾交通流交织区换道模型及自动驾驶汽车控制策略进行研究。近年人机混驾条件下无人驾驶车辆换道行为研究较多，Kanaris 等[2]对无人驾驶车辆合流和换道问题进行了分析并给出了在紧急制动条件下换道最小安全距离的计算方法，并针对不同类型车辆制动情况给出特定最小安全距离；黄玲等[3]基于深度学习理论,构建了人机混驾环境下基于LSTM的无人驾驶车辆换道行为模型；孟鑫[4]以博弈论思想为基础,量化计算自动驾驶车辆换道收益，采用纳什均衡的方法对模型进行求解，得到交织区人机混驾下自动驾驶车辆最优换道策略；Liu 等[5]以传统元胞自动机模型为基础，针对自由换道行为和强制换道行为设计了2套换道规则，通过仿真分析了自动驾驶车辆对异构交通流动力学的影响；田勇达[6]在混流条件下对协同换道中的后车减速协同与强制性换道进行了区分，并建立了多主体动态协同换道模型。现有研究多集中于人机混驾交通流中基本路段和分合流区的换道行为研究，且多数考虑了人工驾驶车辆的换道行为对自动驾驶车辆的换道策略的影响。故交织区换道行为研究也需在对人工驾驶车辆影响因素，应考虑人工驾驶换道行为统计分析的基础上，从宏观交通流的总体通行效率、稳定性出发，确定自动驾驶车辆换道决策。

在交织区换道研究方面，刘有军等[7]在构建交织区元胞自动机模型时考虑了换道压力对换道行为的影响，换道车辆在靠近交织区末端仍未实施换道时会减速并迫使目标车道后车减速以提供足够的换道间距。对交织区的换道模型选取可通过空间位置进行划分，彭博等[8]基于高精度车辆轨迹数据，划分上下游、交织影响区等多个分区，独立设置变量与规则进行建模；Hao等[9]提出了描述交织区换道位置特征的强制换道概率密度模型；曹珊[10]对车辆换道行为的特性进行了深入剖析，对已有的换道模型进行归纳总结，比较它们的优缺点，再根据元胞自动机的原理建立了城市道路换道模型，考虑换道的各种情况和驾驶员的自身的影响因素，提出了换道压力的概念，并据此对于强制性换道和自由性换道分别给出了换道概念模型。现有研究指出在交织区的不同区段人工驾驶车辆换道行为存在明显差异，且行为变化分布存在一定规律，故有必要分区段构建其换道模型，并基于实车数据统计分析其换道行为切换点分布规律，为自动驾驶车辆模型切换决策提供依据。目前，已有学者关注到分流区模型切换方面的研究，即在饱和交通流下，驾驶员会采取激进型和保守型2种不同的强制换道策略[11]。Gong等[12]提出了出口匝道由保守型换道至激进型换道的位置优化模型；钟异莹等[13]在此基础上基于正态分布提出了分流区保守型换道和激进型换道的切换条件。

交织区车辆换道行为特性与基本路段存在较大差异，因其换道均属强制换道，人工驾驶车辆会随距出入口位置的不同呈现不同的换道特性。现已有学者关注到普通交通流分流区行为变化即换道模型切换对道路通行能力的影响，但交织区交通流运行状态与分流区有显著差异，主路与匝道车辆之间的干扰更突出，对于换道模型的切换条件仍需进一步分析得出。自动驾驶车辆的模型切换点位置控制较于人工驾驶车辆模型切换更容易实现，故有必要结合交织区交通流运行状态分别构建各区段人工驾驶车辆和自动驾驶车辆换道模型，并在统计分析人工驾驶车辆换道行为切换点分布函数的基础上，从宏观交通流总体通行效率、稳定性出发，确定自动驾驶车辆模型切换点，以期提高人机混驾条件下高速公路交织区通行能力。

基于最小安全距离模型构建自动驾驶保守型换道即协同换道模型，并分别选取了交织区人工驾驶保守型、人工驾驶激进型、自动驾驶激进型换道模型通过分析NGSIM 在交织区的轨迹数据，得出人工驾驶换道车辆保守型换道及激进型换道的位置分布规律，在SUMO 微观交通仿真平台对自动驾驶换道模型不同切换位置下的混合交通流进行仿真，进而分析自动驾驶车辆保守型和激进型换道对交织区交通流的影响，得出自动驾驶车辆模型最佳切换位置。

1 车辆换道模型构建

1.1 自动驾驶车辆换道模型

相对于传统的人工驾驶车辆，自动驾驶车辆对安全距离、可接受间隙的判断不同，换道所需反应时间和加速度不同，自动驾驶车辆之间还可通过信息交流实现协同换道。文中自动驾驶车辆指完全自动驾驶等级，即由车辆自主完成所有驾驶操作，并会感知到周围联网车辆的换道决策信息，从而形成协同换道现象。

在交织区的换道可分为不实施协同换道和协同换道；而协同换道可分为与前车协同换道和与目标车道前车协同换道2种情况。2种情况下换道所需间隙也不同，论文基于人工驾驶最小安全距离及自动驾驶协同换道行为相关研究[14-15]，构建不同类型自动驾驶车辆间协同换道所需间隙的计算方法。

1）不实施协同换道。当换道车辆为自动驾驶车辆，原车道前车或目标车道后车同为自动驾驶车辆但无换道需求，或原车道前车及目标车道后车均为人工驾驶车辆时，换道车辆无法实施协同换道，换道过程无需附近车辆配合。设换道车为M，原车道前车为O，目标车道前车为DL，目标车道后车为DF，换道类型为强制性换道。设L1为M与原车道前车OL的距离，L2为M与目标车道前车DL的距离，L3为M与目标车道后车DF的距离。设t时刻M车前进方向轨迹切线与车道边界线夹角为β，则有

式中：L为车身长度，m；β为M车前进方向轨迹切线与车道边界线夹角，°；V为车辆速度，m/s；τ为反应时间，s；t为M换道过程所需时间，s；aM为车辆换道跟驰过程中的加速度，m/s2，应根据自动驾驶和手动驾驶的差异性分别进行设置；aemg为车辆紧急刹车的加速度，m/s2。

2）与前车协同换道。在换道间隙达到一定长度时，具有换道需求的前后2辆车可同时进行换道，此时所需换道间隙相较2辆车单独换道间隙之和更小。此类换道车辆编号与位置关系见图1。

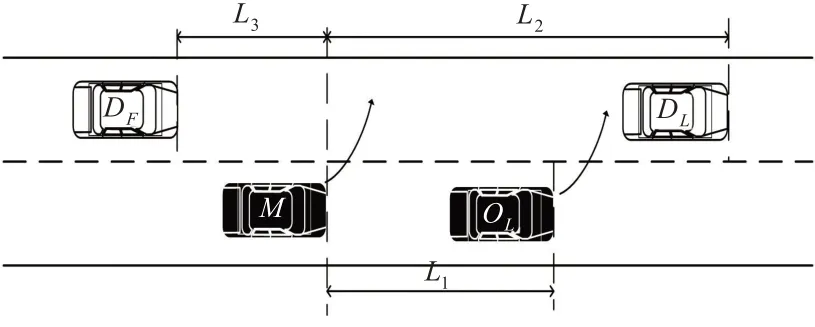
图1 协同换道示意图Fig.1 Schematic diagram of cooperative lane change

在与前车协同换道时，因2 辆车均为自动驾驶车辆，所需反应时间较短可忽略，自动驾驶车辆进行速度调整以满足协同换道所需间隙要求，则可根据式（1）～（3）所采取换道间隙计算方法对该类协同换道所需间隙进行改进。其中，因M与OL协同换道，L1保持为M实施换道过程中因车身偏转而产生的最大纵向位移；L2须同时考虑OL换道所需间隙，则有L1，L2计算见式（4）～（5）。

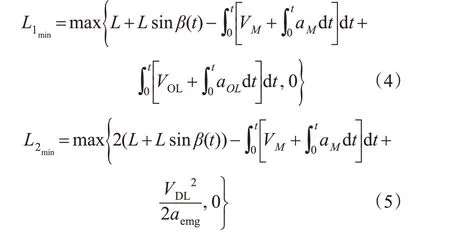
3）与目标车道前车协同交叉换道。当换道车辆和目标车道前车同时有换道需求时，换道车辆与目标车道前车的换道决策对应目标分别为对方的原车道。换道车辆与其目标车道前车的换道决策会互相影响，2辆车同时换道时所需换道间隙更小。此类换道车辆编号与位置关系见图2。

图2 交叉协同换道示意图Fig.2 Schematic diagram of cross coordinated lane change

在与目标车道前车协同换道时，因M与DL协同换道，L1须考虑M与DL换道过程中所需间隙；L2须同时考虑M与OL换道所需间隙，则有L1，L2计算见式（6）～（7）。

在间隙接受理论模型的基础上，因强制性换道存在紧迫性，当车辆到达激进型换道起始位置xm～后仍未完成换道，则M将会调整自身速度，以增加与目标车道前车DL的距离[10]。自动驾驶车辆的激进型换道根据目标车道车辆类型的不同将自动驾驶激进型换道分为目标车道后车为人工驾驶和目标车道后车为自动驾驶2种情况。

1）目标车道后车为自动驾驶。在2辆车同为自动驾驶时可进行信息传递，目标车道后车在没有换道需求的情况下会自动进行减速以满足换道间隙，换道车辆无需进行加减速行为，计算见式（8）～（9）。

式中：VDF(t)为目标车道后车速度，m/s；bDF为目标车道后车减速度，m/s。

2）目标车道后车为人工驾驶。在此情况下换道车辆需进行减速行为，同时迫使目标车道后车进行减速以满足换道间隙，计算见式（10）～（11）。

式中：VM(t)为在t时刻换道车辆M的速度，m/s；Δt为调整速度时间，s；VDL(t+Δt)为换道时目标车道前车速度，m/s；bM为M车减速度,m/s2。

1.2 人工驾驶车辆换道模型

人工驾驶车辆保守型换道所需间隙与自动驾驶车辆保守型相似，但自动驾驶车辆换道反应时间小于人工驾驶车辆，即τ取值不同，本文设自动驾驶车辆为0.5 s，人工驾驶车辆 为1.5 s。计算见式（1）～（3）。

人工驾驶车辆激进型换道与目标车道后车为人工驾驶时自动驾驶车辆换道情况相似，即换道车辆与目标车道后车间没有信息交互，换道车辆减速并迫使目标车道后车减速以实现换道间隙。二者换道反应时间即τ取值不同，计算见式（8）～（11）。

2 人工驾驶换道点分布拟合

为对人工驾驶中交织区换道位置分布及换道冲突策略类型进行量化分析，本文选取NGSIM 中US-101和天津市津保立交桥交织路段车辆交织换道轨迹做基础数据。交织路段示意图见图3和图4。由于激进型换道车辆在换道过程中会迫使目标车道后车减速以满足换道间距，因而将换道时目标车道后车加速度为负的换道过程视作激进型换道。截取NGSIM交织区路段车辆换道轨迹，识别5s内目标车道后车加速度为负的作为激进型换道。分别对NGSIM中US-101路段和津保立交桥主路-匝道及匝道-主路的保守型和激进型换道位置进行高斯拟合，其不同类型换道分布见图5。

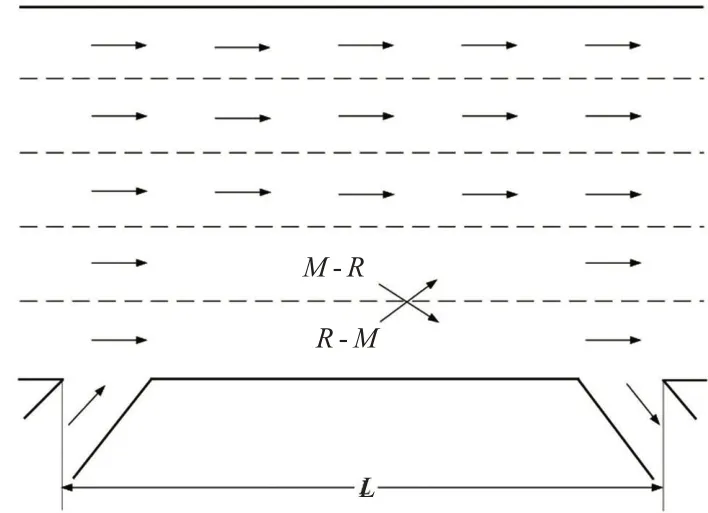
图3 津保立交桥交织区构造图Fig.3 Structural diagram of Jinbaointerchange weaving section

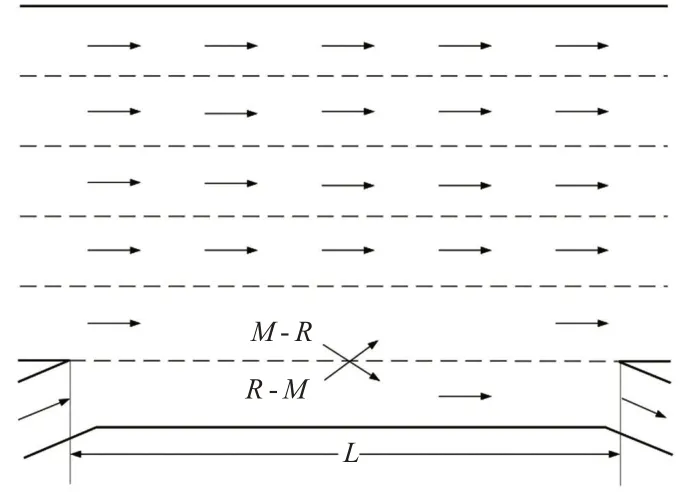
图4 US-101交织区示意图Fig.4 US-101 weaving section diagram

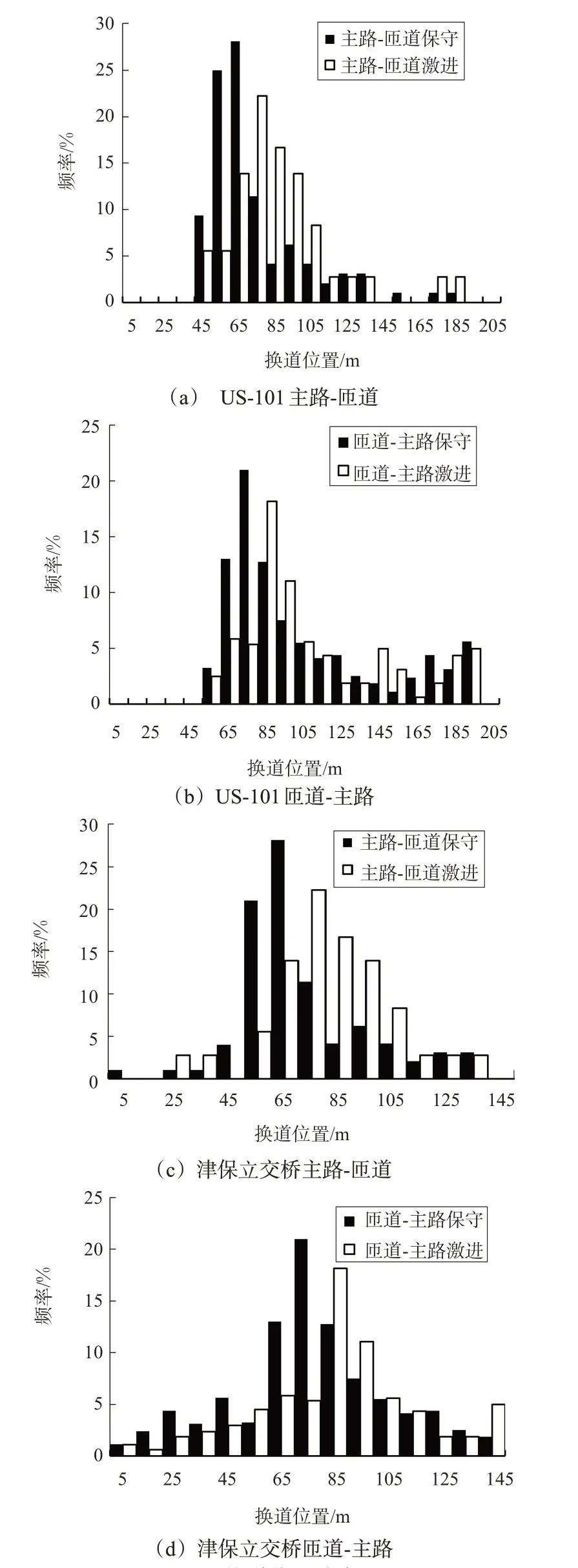
图5 换道位置分布图Fig.5 Lane change location distribution

由origin进行拟合分析可得，主路及匝道的保守型、激进型换道点均为正态分布，该分布的表达式见式（12），US-101中4种分布的均值与标准差见表1。

表1 高斯分布参数表Tab.1 Gauss distribution parameter

由图5 和表1 可见：4 种换道类型换道点均呈现一定的离散性，这是驾驶员风格差异性导致的必然结果，4种换道类型方差不会随交织区长度变化而产生明显变化。利用US-101和津保立交桥均值数据，可进一步建立交织区长度与人工驾驶车辆4种换道类型换道位置，即换道点距交织区起点距离之间的线性关系函数见表2。

表2 高斯分布均值Tab.2 Gauss distribution mean

3 自动驾驶最佳换道模型切换点确定

3.1 仿真实验设计

经相关研究可知，交织有效长度约为200 m[16-17]，交织路段过长时无法体现交织车辆对直行车辆的干扰，为体现交织路段不同位置因强制换道行为而出现的速度变化，设交织区长度为250 m。因人机混驾交通流自动驾驶缺乏实车数据，通过SUMO 微观仿真平台进行仿真实验确定自动驾驶最佳换道模型切换点。实验构造3车道A类交织区，并分别在右侧2车道前部、中部和后部布设瞬时感应检测器，交织区整段布设长度为250 m 的E2 检测器以记录车辆类型、车速、换道位置、排队长度等相关数据。

在SUMO 微观仿真平台可运用Python 语言通过TRACI接口对人工驾驶和自动驾驶的保守型、激进型换道决策进行控制。即在确定车辆类型后，根据控制车辆类型不同确定其换道模型切换点，在未到达切换点时分别采取人工驾驶和自动驾驶的保守型换道模型；在到达切换点后分别实施激进型换道。其控制决策逻辑见图6。

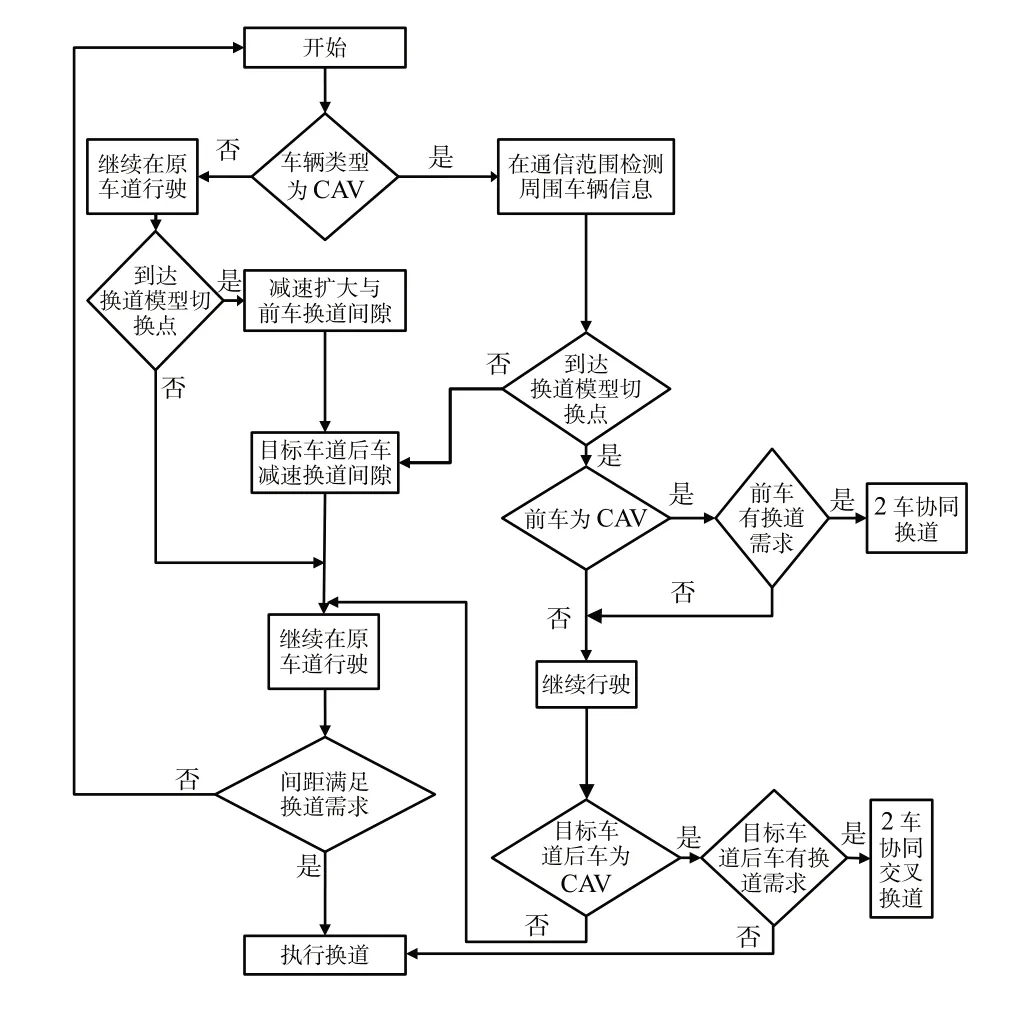
图6 换道控制决策图Fig.6 Lane change control decision diagram

崔居福等[18]通过模拟不同场景下的交通状况对SUMO 平台下6 种跟驰模型进行了对比分析，实验结果表明Krauss模型能较真实反应车辆驾驶行为，故仿真时采用Krauss 模型人工驾驶车辆；在关于自动驾驶及网联车辆的大量研究中，智能驾驶员模型因可通过车-车通信以获得前车信息并实现智能驾驶的特点而被广泛应用[19]，自动驾驶车辆选取IDM车辆跟驰模型。设自动驾驶车辆渗透率由0%至100%以10%为单位递增进行仿真实验，在交织区0～250 m 之间以10 m 为单位设置自动驾驶车辆保守型-激进型最佳换道模型切换位置，假设车辆到达率符合泊松分布，进行24 h 仿真实验并进行结果分析，以便充分体现自动驾驶车辆对交织区交通运行状态的影响，根据交织区人工驾驶车辆主路-匝道和匝道-主路保守型换道及激进型换道拟合结果，结合交织区长度设置本次仿真环境下人工驾驶交通流分布，进而确定不同渗透率下的自动驾驶车辆佳换道模型切换点，仿真实验中交织区及车辆仿真参数取值见表3[20]。

表3 仿真参数表Tab.3 Simulation parameter

考虑到自动驾驶车辆换道位置完全可控，以及自动驾驶车辆保守型换道“与目标车道前车协同交叉换道”实现的概率提升，最大限度改善交织区交通运行质量，提升交织区通行能力，将自动驾驶车辆主路-匝道、匝道-主路这2类换道车辆的最佳模型切换点位置统一，并通过仿真实验以交织区交通运行状态、通行能力优化为目标确定交织区换道模型最佳切换点位置。

3.2 自动驾驶换道模型切换点确定

交织区所通过的交织车道最大流率、交织区车辆平均速度、换道平均速度可较好的反应交织区运行状态优劣，优化其指标结果均可从一定程度提到交织区通行能力。以15 min 为观测单位求算流率，得出不同渗透率下自动驾驶车辆换道模型切换点位置对交织车道流率、平均速度和换道平均速度的影响见图7～9。

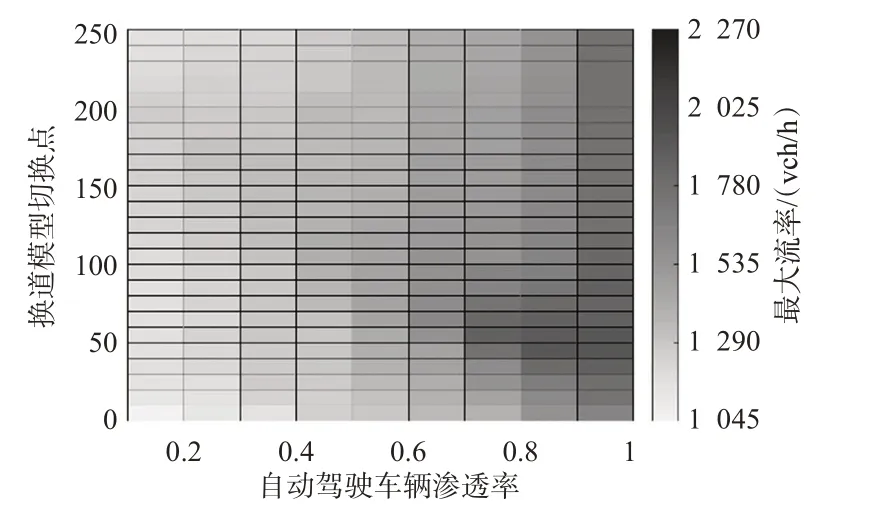
图7 不同渗透率下换道模型切换点与最大流率分布图Fig.7 Distribution of starting points of radical lane change under different mixing rates

由图5 可见：随着自动驾驶车辆渗透率的提高，换道模型切换点的最佳位置逐步向交织区起点移动，在自动驾驶渗透率逐渐大于50%后，模型切换点位置对流率的影响愈加明显；当渗透率达到100%即完全自动驾驶状态时，换道模型切换点在30 m左右处达到最大流率2 269.6 veh/h；且从90 m 继续后移过程中，最大流率不再发生变化，这是由于在完全自动驾驶状态下，交织车辆通过协同换道已在交织区前半端完成换道过程，换道模型的切换不再对其产生影响。在自动驾驶车辆低渗透率和高渗透率环境中，模型切换点位置调整对流率的影响弱于中等渗透率环境中，主要原因是中等渗透率条件下，人工驾驶车辆与自动驾驶车辆之间的相互干扰更多，当模型切换点逐渐向最佳模型切换点靠近时，自动驾驶车辆的换道决策更好的适应了人工驾驶车辆的换道行为和换道点分布特征，最大限度将2 种车型间的相互干扰降到最大，可有效提升交织区最大流率。

图9 不同渗透率下换道模型切换点与换道平均速度关系图Fig.9 The relationship between the switching point of the lane-changing model and the average speed of the lane-changing under different permeability

由图8～9可见：随着自动驾驶渗透率的提升，交织区车辆平均速度和换道速度因换道模型切换点位置变化产生的差异呈逐渐减小趋势。主要原因是自动驾驶车辆占比提高后，保守型换道中的“与前车协同换道”以及“与目标车道前车协同交叉换道”协同换道行为实现概率大幅提升，大部分车辆有望在速度不发生改变的情况完成协同换道，换道车辆无需牺牲自身速度及目标后车速度进行激进型换道，因而换道模型切换点位置对交织区车辆速度影响逐渐降低。

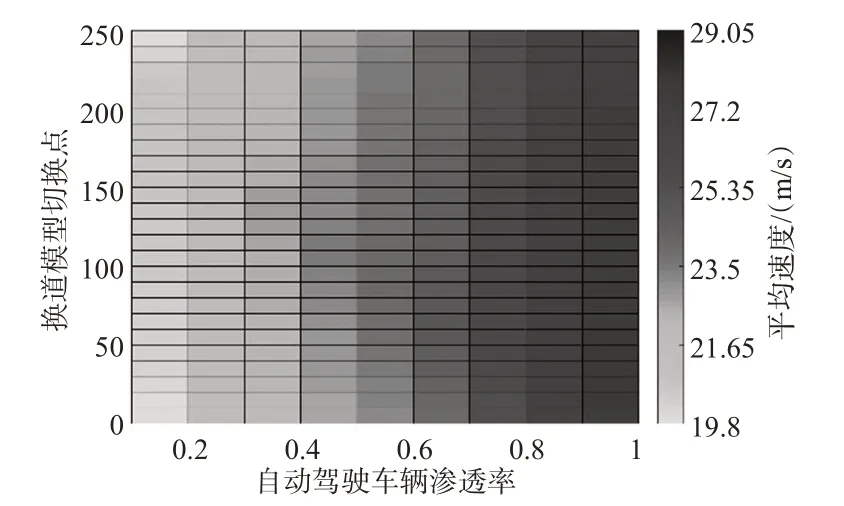
图8 不同渗透率下换道模型切换点与平均速度关系图Fig.8 Switching point and average velocity under different permeability distribution of lane changing model

综上，得出不同渗透率下使3 个指标最优的自动驾驶最佳模型切换点见表4。

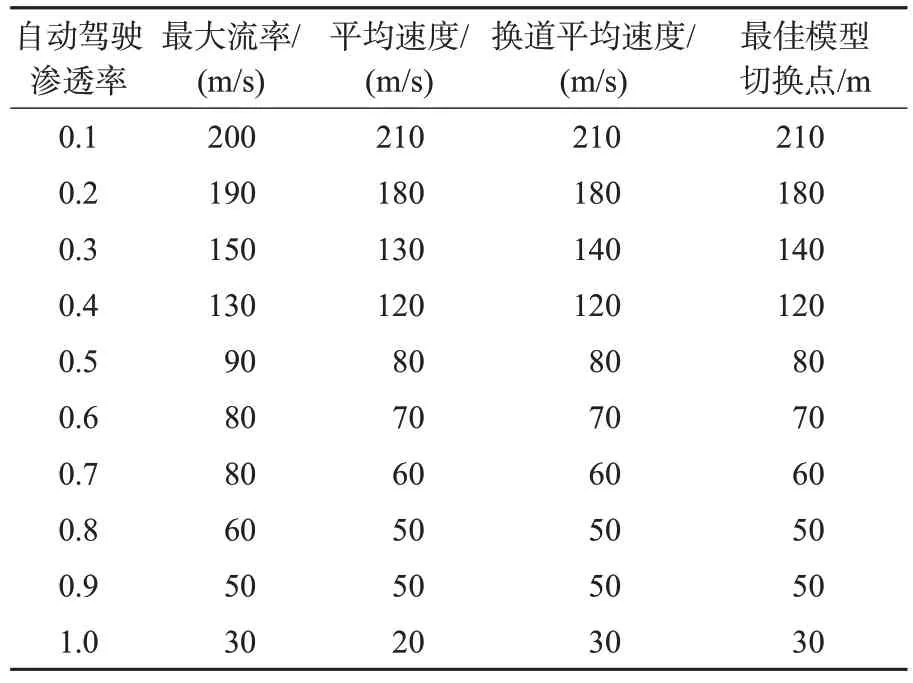
表4 不同渗透率下自动驾驶最佳模型切换点Tab.4 optimal model switching points of automatic driving under different permeability

3.3 仿真实验对结果的影响

在跟驰模型及换道模型选取方面：仿真中人工驾驶车辆均统一采用的Krauss模型是1种安全距离类模型，即在单位步长内车辆保持固定加速度行驶并更新位置。在仿真步长较大的情况下，车辆位置更新频率降低，易出现换道不及时现象，从而使换道位置后移。自动驾驶车辆统一采用IDM 模型，这个模型随机性较小，即当运行状态相似的2 自动驾驶车辆同时驶入时，将并步向前行驶，并保持相同的行驶状态，与实际情况不符。这一影响会使仿真结果较为单一。仿真中所用换道模型为间隙接受模型，在无协同的保守型换道模式下，默认换道车辆在目标车道满足最小安全间隙后立刻执行换道。在人工驾驶车辆仿真中忽略了现实车辆运行过程中根据驾驶员风格差异性其换道所需间隙不同，且均大于最小安全间隙。这一差异性会增加交织区车辆换道频率，使车辆换道位置向交织区起点移动，对应自动驾驶最佳模型切换点会产生向交织区起点的偏移。

在仿真平台及实验过程方面：仿真所采用的SUMO仿真平台，车辆在换道中并未设计换道轨迹，而是在遇到合适间隙后瞬间插入；而在实际车辆运行中因存在换道车辆的横向运动轨迹，对目标车道后车的跟驰行为会产生一定影响，降低后车行驶速度，交织区车流整体速度降低。仿真模拟情景与实际车辆运行状态存在差异，车流平均速度较高，从而使换道频率增加，车流换道位置向起点处前移。仿真中设置步长为0.1，与实际相比仿真精度仍存在不足，存在部分车辆在仿真步长内错过换道间隙而未及时换道的情况，仿真所得换道位置分布会产生微量的后移，对应自动驾驶最佳模型切换点向交织区末端有微弱偏移。

在仿真实验设备方面：因控制过程中逻辑判断环节较多，计算机处理过程较慢，故采取在仿真中以15 min 为观测单位计算流率。仿真时长较小，无法全部模拟实际车辆运行中所有运行情况，因而实验结果较为单一，仿真所得换道位置分布同样会向交织区起点处偏移，对应自动驾驶最佳模型切换点同样会产生向交织区起点的偏移。

此外，在仿真中对车辆现实运行中因气候、路面情况、昼夜、驾驶员心理等造成的随机性体现不足，实验结果较为理想。

4 结束语

本文对津保立交桥和NGSIM 轨迹集中US-101交织区轨迹数据中车辆换道位置分布进行了拟合，二者均符合高斯分布且趋势相近，高斯分布均值随交织区长度增长而提高，并进一步探究了交织区长度与不同类型换道位置的关系，在此基础上总结归纳了主路-匝道人工驾驶车辆、匝道-主路人工驾驶车辆2种换道的保守型-激进型换道模型切换点分布函数；分别以最大流率、交织区整体车辆平均速度、交织车道换道平均速度最优化为标准确定自动驾驶车辆保守型-激进型换道模型切换点，并进行对比分析，得出结论：在自动驾驶渗透率为10%时，换道模型切换点位于210 m 左右处最大流率达到最高；随着自动驾驶车辆渗透率的提高，换道模型切换点的最佳位置逐步向交织区起点移动；当渗透率达到100%即完全自动驾驶状态时，换道模型切换点在30 m左右处达到最佳。

未来将对不同交织区长度下其最佳换道模型切换点进行研究，以探讨交织区长度对自动驾驶车辆切换点选择的影响，同时因缺乏自动驾驶交通流轨迹数据，对自动驾驶换道模型相关参数的选取停留在仿真阶段，在未来的研究中考虑通过实车实验进行参数标定。