无线体域网安全路由算法设计与仿真

冯 维， 许 丹， 夏晓威， 李 沛

（1.杭州电子科技大学通信工程学院，杭州 310018；2.华信咨询设计研究院有限公司移动研究院，杭州 310015）

0 引 言

无线体域网（Wireless Body Area Network，WBAN）是一种以人体为中心的短距离通信网络，由置于人体周围、体表以及体内的传感器节点和一个中心节点构成，用于检测人体生理数据或周边状况信息。WBAN已被应用于各种场景，如消费电子、医疗领域以及运动训练等，成为未来智能化医疗健康服务的技术核心［1］。

WBAN的早期研究可以追溯至2000年著名学术期刊《Nature》上发表的无线内窥镜论文［2］，该论文的发表为后续人体可穿戴／植入医疗设备组网技术的发展提供了新的方法。大量学者针对WBAN展开了研究。学者们研究了WBAN的能耗问题［3］，信道特征［4-5］，通信协议架构［6］，拓扑设计［7］等；同时，考虑到传感器节点通常收集并传输生命体征信息，存在极强的实时性要求，部分学者展开了WBAN时延优化研究；考虑到WBAN采集和传输的数据大多为用户个人的健康监测信息，属于个人隐私，针对WBAN安全性的研究也成为热点。本文旨在考虑WBAN路由安全问题的基础上优化系统的传输时延。

传统基于密码学的数据保护［8］需要高性能的硬件支持，且计算量巨大，无法应用到WBAN中。本文考虑通过物理层安全技术［9］来实现WBAN的传输安全问题。由于WBAN信道模型需要同时考虑体内信道与体外信道，而体内信道服从对数正态分布，这一特性导致对于WBAN的物理层安全的定量分析无法像通用无线多跳网络一样计算求解，目前WBAN考虑物理层安全的优化算法基本基于博弈论［9，11］来实现。对于博弈手较多、博弈因素较多的网络，博弈论的算法复杂度非常高，这一因素导致这些算法的应用也非常有限。基于此，通过马尔科夫决策模型来研究WBAN的物理层安全传输问题。

根据WBAN体内体外信道的信道分布，推导出链路的安全中断概率（Secrecy Outage Probability，SOP），以安全中断概率为约束的WBAN时延最小路由选择问题建模为寻找动态系统最小时延成本的控制策略问题，运用实时动态规划算法得到安全路由算法。通过虚拟仿真，学生能够运用Matlab软件平台，更直观地模拟该无线通信系统，对体域网、无线信道、路由、网络安全和动态规划等知识都将有更深入的了解。

1 系统模型

考虑一个如图1所示的WBAN。图中右脚踝处为中心节点，用于收集和转发数据信息到互联网。除此之外还有5个传感器节点，用于采集信息，并以直接或间接方式将信息发送给中心节点。体外存在一个窃听者，在合法节点传输消息过程中窃听信息。

图1 WBAN示意图

1.1 安全中断概率及连接成功概率

在WBAN中，信道可分为体内信道和体外信道两种类型。合法节点通过体内信道传递消息，将体内信道称为主信道，主信道建模为对数正态衰落信道，其接收信噪比遵循对数正态分布。窃听者通过体外信道进行窃听，窃听信道建模为瑞利衰落信道，其接收信噪比遵循指数分布。

若要保证主信道传输的信息在接收端能够正确解码，应满足以下条件：

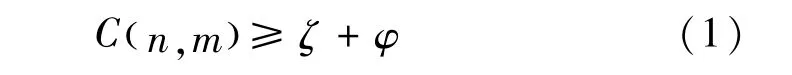
式中：n、m分别为发送节点和接收节点；C（n，m）为链路nm的瞬时速率；ζ为随机速率；φ为保密速率。

与此同时，假设主信道的信道增益服从均值和方差分别为μ和σ2的对数正态分布，则可获得从发送节点n到接收节点m的连接成功概率

式中：ρ为单位距离的发送信噪比；gnm定义为链路nm的信道增益；dnm为发送者n和接收者m两者间的距离；α为路径损耗因子；P[]·为概率算子；erf（·）为误差函数。且

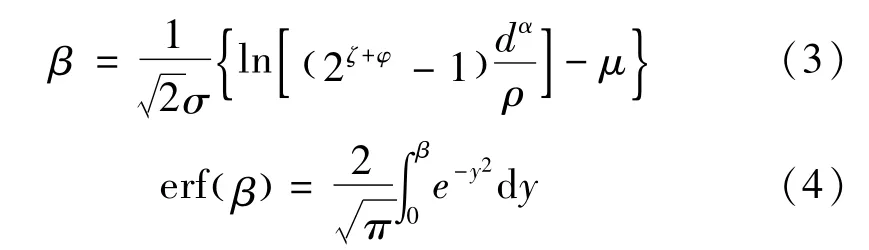
根据物理层安全的定义［12］，为实现信息的完全保密，也就是说，窃听者最多窃听到ζ部分的消息，而得不到任何与φ有关信息，窃听速率应当满足

式中，z为体外窃听者。

由于窃听信道服从指数分布，可推导出发送节点n的安全中断概率

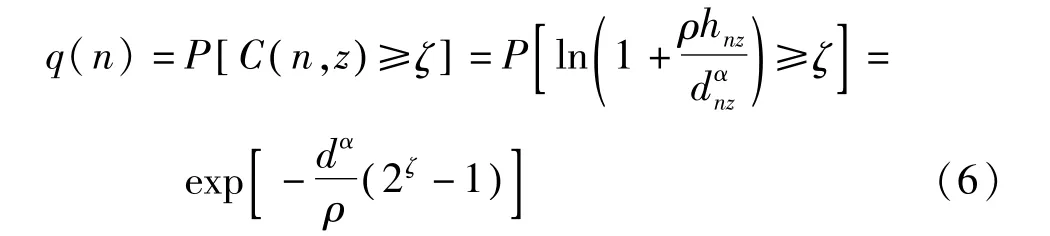
式中：dnz为发送者n和体外窃听者z两者间的距离；hnz为窃听链路nz的信道增益，其服从均值为1的指数分布。

假定已知路由跳数i＝0，1，…，I，则整条路由的安全中断概率为：

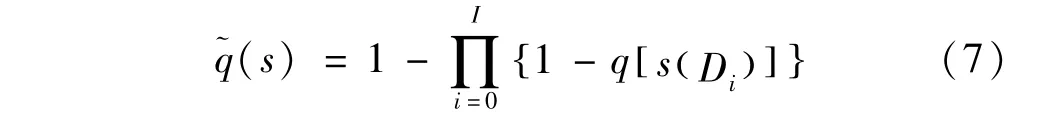
式换s(D中到i)： 为ss(＝ 第D{Is)i(的次D0一状)，系态s(列转D1有移)，…时序，，状s在(态D已I集)解}；为 码s由(的D状0节)态为点源s集(D节合0点)转D；i中选择的动作（即发送节点）。在这一过程中，当且仅当保证每条链路的安全，才能使整条路由安全；q[s(Di)]为当发送节点为s(Di)时的安全中断概率

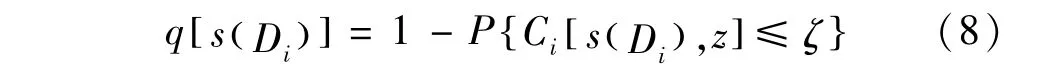
1.2 马尔科夫状态转移概率

系统状态x由[ D(x)，ω(x)]这两个因素决定，D(x)⊆L为在x状态之前阶段全部已经解码该保密信息的合法节点集合；L为全部合法节点的集合；ω(x)为保密信息是否被窃听者所窃听。当在x状态下保密信息被窃听到，则ω(x)＝1；否则为0。A(·)为传输调度策略，即在某一状态下可以作为发送机的节点。此时，离散马尔科夫链由状态x转移到状态y有以下4种情况：

（1）由g∉D(x)，ω(x)＝0的状态x，转移到ω(y)＝0，D(x)⊆D(y)的状态y；

（2）由g∉D(x)，ω(x)＝0的状态x，转移到ω(y)＝1，D(x)⊆D(y)的状态y；

（3）由g∉D(x)，ω(x)＝1的状态x，转移到ω(y)＝1，D(x)⊆D(y)的状态y；

（4）由g∈D(x)的状态x，转移到g∈D(x)的状态x。

式中，g为目标节点。从状态x到另一状态y的转换是一个随机事件，具体取决于在x状态下的动作A[D(x)]。πxy（a）为在采取动作a（a∈D(x)）的前提下，从状态x转移到状态y的状态转移概率πxy（a）＝

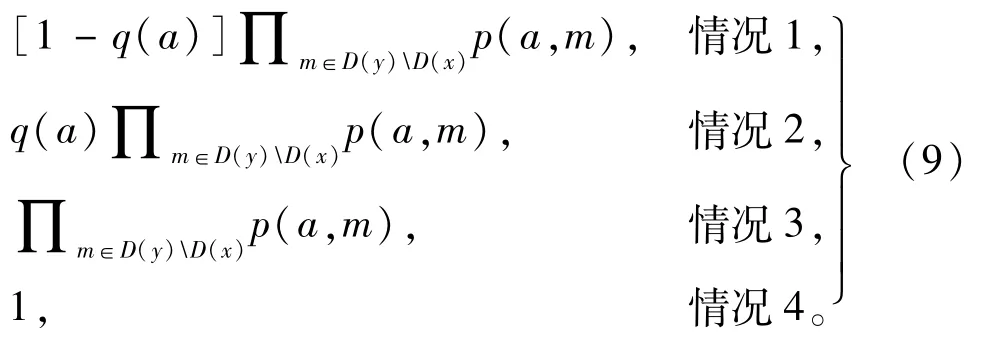
式中，m为从状态x转移到状态y过程中新增的已解码信息的节点。其他不满足这4种情况的转移概率定义为零。

1.3 优化模型

基于所述马尔科夫链状态转移概率表达式，根据安全中断概率和连接成功概率表达式，建立优化模型，获得在满足安全中断概率约束的条件下最小化平均时延的多跳传输策略，用跳数来描述时延，得到优化模型：

式中：目标函数定义为平均时延，i为第i次状态转移；Di为在第i次状态转移后的已解码节点集合；E[]·为数学期望；c()·为状态转移过程中的代价。第1个约束条件为保密性约束，～q()·为整条路由的SOP，平均SOP的阈值为ε；第2个约束条件为时延约束，目标节点解码消息时的时延为0，否则时延为1；第3个约束为策略约束，A集合表示在没有平均SOP约束的前提下的所有可能策略集。

根据离散马尔科夫链模型中对于窃听的表述，将无线体域网的安全中断概率重新定义如下：

根据式（11），建立新的优化模型如下：

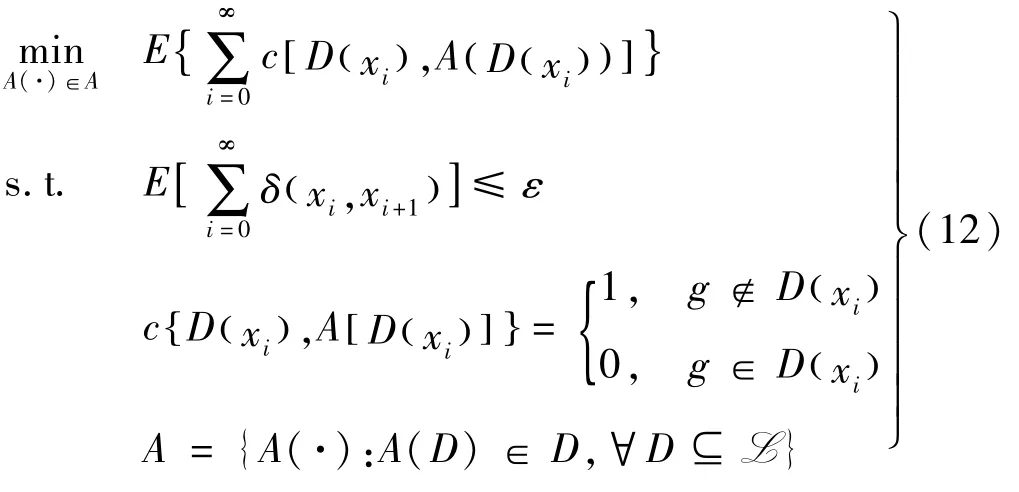
2 基于马尔科夫链的低时延安全路由选择算法

2.1 拉格朗日乘子法

优化问题（12）可以采用贝尔曼理论转换成贝尔曼方程解决［13］。SOP约束的存在使该问题复杂化。考虑拉格朗日乘子法，将SOP约束整合到成本函数中，并寻求路由选择策略和拉格朗日乘子λ的联合优化。根据文献［14-15］中的定理，对于任何λ≥0，如果策略A（·）满足以下最小化问题：

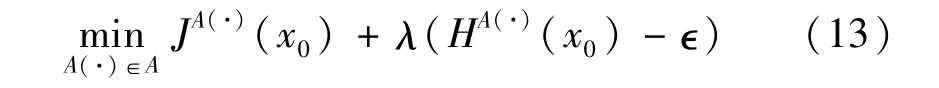
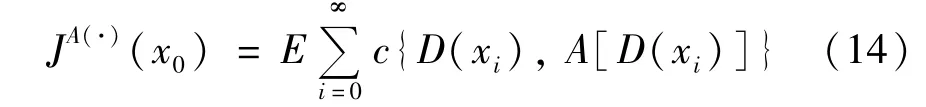
HA（·）（x0）表示安全中断概率约束，

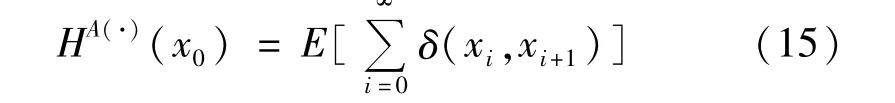
对于式（13）的最优解A*λ（·）相应的SOP约束的值为：

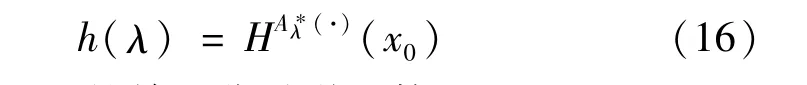
式中，h为变量λ的单调非递增函数。

由于策略A是一个有限且离散的集合，可能没有一个λ值，使得式（14）的解可以满足SOP约束的临界值。在这种情况下，A（·）满足SOP约束，却不是最优的，所以Aλ（·）仍然是式（12）的可行解。如果存在可行的解，对正数范围内进行简单的二分式搜索就可以找到满足SOP约束的最小λ。

对于给定的λ，将选取动作a时状态x转移到状态y的时延成本函数为：

相应地给定λ的无约束目标函数：

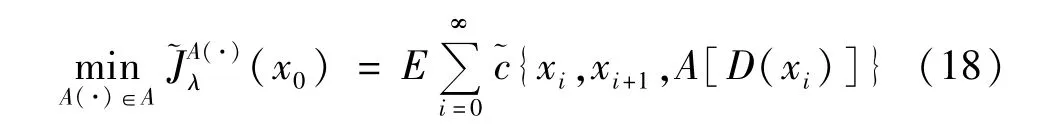
步骤1随机产生一个WBAN网络结构，计算出节点间的距离，根据式（2）、（6）计算出连接成功概率和安全中断概率，并且初始化所有状态值的上限V。

步骤2初始化S为初始状态S0，此时已解码节点只有源节点且保密信息未被窃听。

步骤3根据贝尔曼方程，以概率1－θ选取状态S的最佳动作a；概率θ随机选取状态S的动作集合A（S）中的其他动作。

步骤4执行选取的最佳动作a，依据状态转移概率随机选取一个状态S′，重复步骤3，直到S′为吸收状态，转步骤5。

步骤5根据贝尔曼方程，回溯更新从初始状态到吸收状态转移过程中每一状态值V；重复步骤2～5，直到初始状态值V（S0）与上一次探索试验的差小于阈值τ，则停止运行，并且返回最佳调度策略。

根据贝尔曼优化理论中的价值迭代，可获得贝尔曼方程：［13］

式中，γ∈［0，1）是贝尔曼方程中的折扣因子，N（x）表示状态x的邻居状态集合。

2.2 实时动态规划算法

贝尔曼方程可用实时动态规划算法（Real-time Dynamic Programming，RTDP）来实现。RTDP是一种异步值迭代算法，根据式（19）每个状态x都有一个状态值J（x），在初始化时需要给每个状态一个上限状态值V，从初始状态S0开始，在选择不同的动作情况下，根据后继状态的状态值V计算该状态的值函数，从而选择状态值最低动作，并更新状态值V。在选定动作后，根据其后继状态的分布概率，随机选择下一状态，达到吸收状态后，RTDP会通过返回至S0来终止试验，并更新每个状态的值。

为了防止动作选择时，局限于几个动作，无法快速获得可行解，在算法中加入一个概率θ，以概率1－θ选取状态S的最佳动作a，以概率θ选择其他动作，从而跳出束缚，达到更快收敛的目的。

实时动态规划算法来求解WBAN时延最小的安全路由选择问题，步骤如下：

3 实验结果

为便于数据处理，将图1投影至图2。图2为一个100 cm×100 cm的仿真区域，（0，0）处的节点1为源节点，（100，100）处的节点6为目标节点，（95，5）处为一个窃听者，*为窃听节点，其他都是合法的传感器节点。在此模型中，以头部的传感器节点1作为发送源，右脚踝处的中心节点6作为目的节点，寻找保密信息从源节点传输到目的节点的最小时延安全路由。

图2 平面仿真拓扑

针对安全中断概率阈值∈＝0.05时的情形来详细说明算法的状态决策过程。由于该模型基于离散的马尔科夫链，目标函数值是离散的，所以采用二分法即可获得最佳拉格朗日乘子λ*。当窃听者位置为（95，5）时，仿真可得λ*＝1.92，此时路由安全中断概率为0.041 2，小于阈值，满足约束，平均时延为3.631 4。在此时的不同状态（非吸收状态）对应的最佳发送节点见表1。

因为信息在传输过程中，下一状态是根据概率随机选择的，图3（a）就是表1中某一状态转移过程。在图3（a）中的集合中，第1位的0或者1用于表示在该状态下信息是否被窃听，随后的数字表示在该状态下已经解码信息的节点编号。其中，S0＝{0，1}为初始状态，已解码信息的节点只有源节点（节点1），且此状态下信息未被窃听，因此选择1作为发送节点。下一随机状态为S1＝{0，1，3}，该状态未被窃听且已经解码保密信息的节点有1和3。依据贝尔曼方程此状态下最{0佳，1，的3，发5}送，此节状点态为的节最点佳3发。送随节后点，为下5一。状最态后为转S移2到＝吸收状态S3＝{0，1，3，4，5，2，6}，此时目标节点（节点6）已经解码信息，且此状态下信息没有被窃听。图3（b）是在图3的状态转移过程中最佳策略下的路由1→3→5→6。

图3 状态转移过程及路由示例

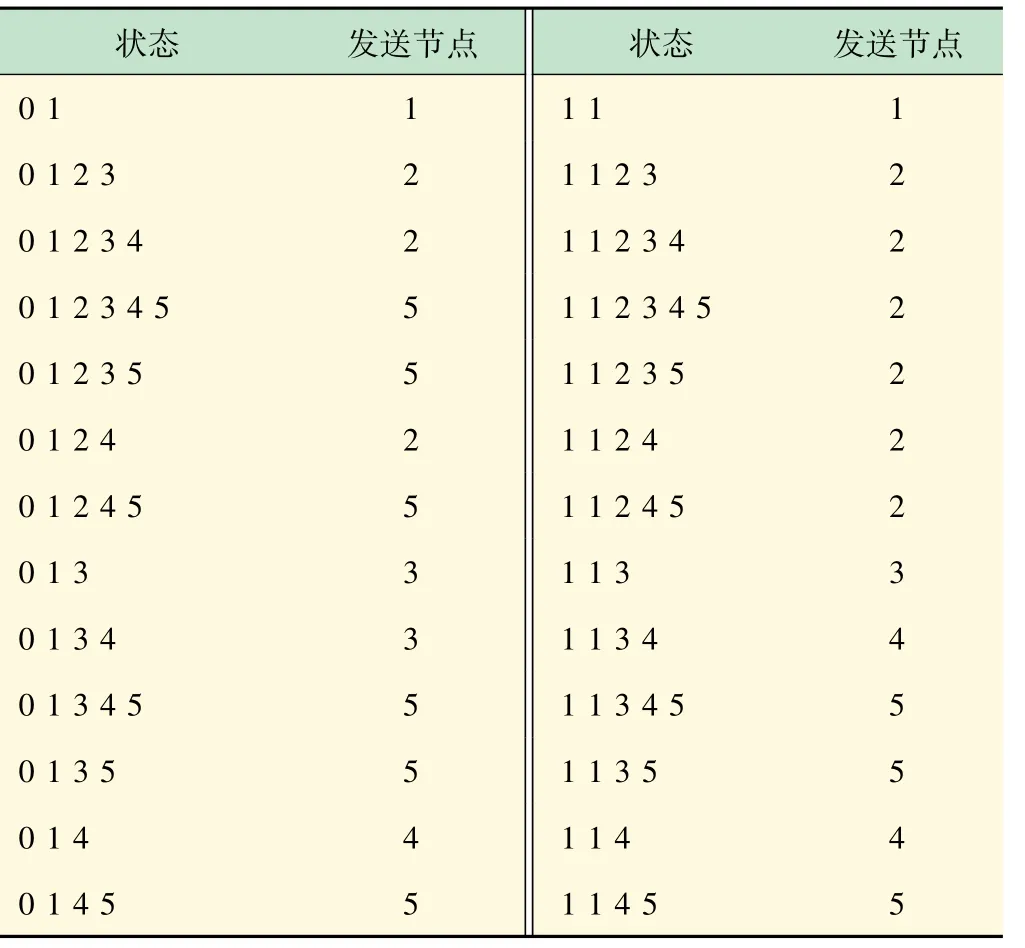
表1 不同状态对应的最佳发送节点

图4、5分别为在窃听者位置（90，10）、（95，5）、（100，0）的情况下，路由安全中断概率和平均时延随着拉格朗日乘子λ的变化曲线。通过引入拉格朗日乘子参数将路由安全中断概率约束的最小化平均时延问题转化成无约束的优化问题，通过迭代找到最优的拉格朗日乘子，获得无优化问题的最优解，即可得到原问题的可行解。由图4、5可知，随着拉格朗日乘子的增加，这两个指标最终均能收敛至最优值。随着窃听者z的位置距离整个拓扑的中心越远，路由安全中断概率和平均时延都越小。这是由于窃听者位置越远，信号衰落越大，窃听者能够窃听的信息越少，整个网络越安全，因此无需以增加跳数（即时延）为代价来换取通信的安全，则平均时延也越低。

图4 窃听者在不同位置时的路由安全中断概率

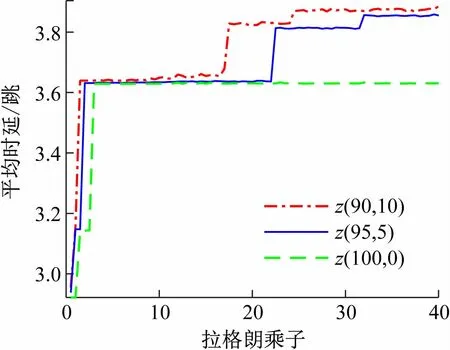
图5 窃听者在不同位置时的平均时延

4 结 语

本文提出一种基于马尔科夫链的无线体域网低时延安全路由算法。将WBAN中安全中断概率约束下的路由选择问题建模为寻找动态系统最小时延成本的自动控制问题，并结合拉格朗日乘子法和实时动态规划算法进行求解，获得在保证安全的条件下的最佳中继节点以及最小时延。通过该实验，学生可以将Matlab仿真技术联系实际通信系统，解决实际通信工程领域的技术问题，培养学生的动手能力和科研能力，并已作为《Matlab与仿真》《无线通信原理与应用》《数据通信与计算机网络》等课程教育实践教学仿真案例应用于通信专业学生教学实践中。