车用余热回收系统涡旋膨胀机涡旋盘应力变形分析
谢东升,刘 祯,李 正
(1.湖北文理学院 纯电动汽车动力系统设计与测试湖北省重点实验室,湖北 襄阳 441053;2.湖北文理学院 汽车与交通工程学院, 湖北 襄阳 441053)
随着膨胀机应用范围越来越广和应用要求不断提高,就透平式膨胀机和活塞式膨胀机而言,涡旋膨胀机作为一种新型容积式膨胀机,具有结构紧凑、体积小、重量轻、能量转换效率高以及可处理小气量膨胀工质等优点[1-2],更能满足人们对其更高的要求,因此近年来在空调制冷、压缩空气储能技术、有机朗肯循环、低温余热回收等方面得到广泛应用[3-6]。在涡旋膨胀机工作过程中,高温高压气体经吸气口进入推动涡旋盘运动,不断增大进气腔与膨胀腔的体积,从而实现气体体积的膨胀,并将气体的压力能转化为机械能[7],在实现整个吸气、膨胀、排气的周期性运作中,膨胀机动静涡旋盘工作环境复杂,不仅受到2个涡旋盘之间的摩擦,还承受着较高的热负荷和气体力,这使得涡旋盘尤其是涡旋齿极易发生变形。变形会使轴向间隙变大,也会对2个涡旋齿的啮合效果以及径向间隙的密封产生影响,从而影响膨胀机的工作性能和可靠性,因此,涡旋膨胀机涡旋盘的变形研究十分重要。
目前,关于涡旋盘的变形研究大都集中在对涡旋盘进行气体力载荷和热载荷分析,得到相应的应力和变形,且研究对象多为涡旋压缩机。郭守宁等[8]通过ANSYS分析软件对气体力作用下的涡旋盘的应力与变形规律作了探讨;杨广衍等[9-10]对温度场下动静涡旋盘产生的热应力和热变形进行了仿真研究;刘振全等[11]对动涡旋盘进行了有限元划分,对其受力下的刚度和强度进行了分析;刘涛等[12]对变截面动涡旋盘的热应力和热变形进行了研究。后来,不少学者又通过耦合的方法对涡旋盘多场载荷下的变形进行了研究,如刘国平等[13-15]对变化的多场载荷进行耦合分析,探究涡旋动盘的应力变形情况。以上研究虽对涡旋盘设计优化有一定的指导作用,但涡旋膨胀机与涡旋压缩机的工作过程以及工作条件不同,两者之间承受的温度载荷和气体力载荷差异较大[16],所以不能用涡旋压缩机的结果来指导涡旋膨胀机的设计优化。
此外,目前对涡旋膨胀机的研究大多为膨胀机内部流场的数值模拟研究[17-19],或者非稳态流动特性分析[20-22],对涡旋盘的变形研究较少。此前,刘祯等[16]通过对比2种不同型线下的流场特性,探讨了不同型线参数对所受温度和压力载荷的影响规律,得到了不同型线膨胀机涡旋齿的变形特性,但并未通过有限元方法对膨胀机涡旋盘的变形进行系统分析。本文通过有限元分析方法,对涡旋膨胀机动涡旋盘进行2种热边界载荷的施加,得到其温度场分布及热变形和热应力结果,并进行对比分析;对所受气体力作用下的变形分析采用基于热力学模型计算和基于流场结果2种方式进行对比研究,最后通过耦合的方法,对膨胀机涡旋盘温度场与气体力共同作用下的变形进行了仿真分析。通过温度场下的对比分析、气体力作用下的对比分析以及耦合作用下的对比分析,更全面的得到涡旋膨胀机涡旋盘形变分布以及应力分布规律,对涡旋膨胀机的强度设计、可靠性研究以及优化改进提供了一定的理论参考。
1 涡旋盘有限元模型的建立
1.1 三维模型建立
涡旋盘几何模型建立的几何参数,主要包括:涡旋齿齿高h、齿厚t、基圆半径R、节距Pt以及涡旋齿圈数N、涡旋盘直径D等。计算公式为:
t=2αR
(1)
Pt=2πR
(2)
(3)
(4)
其中:α为圆渐开线发生角;Ror为主轴偏心距;φe为最终展角;δ为边缘间隙。
本研究中涡旋盘几何参数值如表1所示。

表1 主要几何参数
涡旋型线采用圆渐开线型线,齿头部分采用双圆弧修正法进行修正,依据涡旋型线参数方程建立动涡旋盘的三维模型如图1,其渐开线方程表达式如式(5)所示:
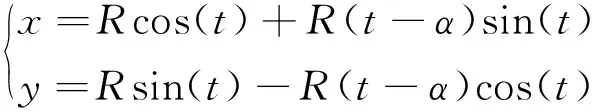
(5)

图1 动涡旋盘三维模型
1.2 材料属性设置
本研究中涡旋盘材料为铝合金4032,其基本参数如表2所示。
1.3 位移约束设置
在涡旋膨胀机实际工作过程中,涡旋盘受气体力作用,主轴顶部紧贴轴承孔顶面,限制了轴向位移,且由于十字滑环,限制了动涡盘发生自转。所以,其位移约束可简化为:
1) 端板周围侧壁Z方向的位移为零;
2) 动涡旋盘轴承孔内壁面X、Y方向的位移为零;
3) 动涡旋盘轴承孔顶部Z方向位移为零。

表2 材料属性
1.4 网格单元划分
在对涡旋盘网格划分时,由于膨胀机实际工况下,端板变形很小,涡旋齿变形较大,所以对涡旋齿采用较为精细的正六面体网格划分,端板采用自动网格划分,设置全局网格尺寸2.5 mm。划分网格后的有限元模型共有23 040个单元,67 823个节点,如图2所示。

图2 有限元模型
2 温度场作用下的应力变形分析
2.l 2种温度边界设置
2.1.1基于线性变化的温度场设置
根据某车用发动机有机朗肯余热回收系统实际工况,设定进气温度为132 ℃,出口温度为47 ℃,环境温度为25 ℃。在ANSYS Workbench中建立稳态热分析模块,由涡旋盘几何特性和温度分布特性分析,可在柱坐标系下通过端板半径的变化来表达温度的分布情况。于是,在圆柱坐标系下,可将涡旋盘的温度简化为沿端板半径方向呈线性变化的温度场分布,其变化规律为:
T=47+85(1-x/79)
(6)
式中:x为柱坐标下涡旋盘端板变化半径(mm);79为涡旋盘端板最大半径(mm);85为进口温度与出口温度的差值。
2.1.2基于流场温度的温度场设置
由该涡旋膨胀机的流场数值模拟结果,以涡旋齿始端为起点,沿涡旋齿壁面连续选取相邻间隔相同展开角阈值的位置的点。本文以间隔π/6选取,探查其温度值,可获得膨胀腔内涡旋盘壁面的部分流场温度值,通过对温度值进行平均化处理,得到动涡旋盘壁面的边界热载荷。在进行温度场设置时,利用Workbench环境中的表格数组进行加载,可得到涡旋齿的温度场分布;此外,因涡旋齿受温度影响严重,涡旋盘端板影响很小,为方便载荷施加,对涡旋盘端面仍施加分布规律为:T=47+85(1-x/79)的线性温度,亦能体现端面的分布情况,对整个涡旋盘的温度分布影响很小,能有效的模拟涡旋盘的温度场分布
2.2 2种温度边界下的模拟结果分析
本研究中选取吸气结束时,对动涡旋盘在2种温度边界下进行热应力和热变形分析,分别得到线性温度场下的结果云图3和基于流场温度下的结果云图4。由2种温度边界下的分析云图可知,高段温度均出现在涡旋齿齿头部分,且由中心向外围逐渐降低,但基于流场下的温度场分布更符合实际情况。在热载荷作用下,最大变形发生在涡旋齿齿头部分,且顶部位置更加突出,并呈现由齿头向齿尾非线性逐渐减小的趋势。
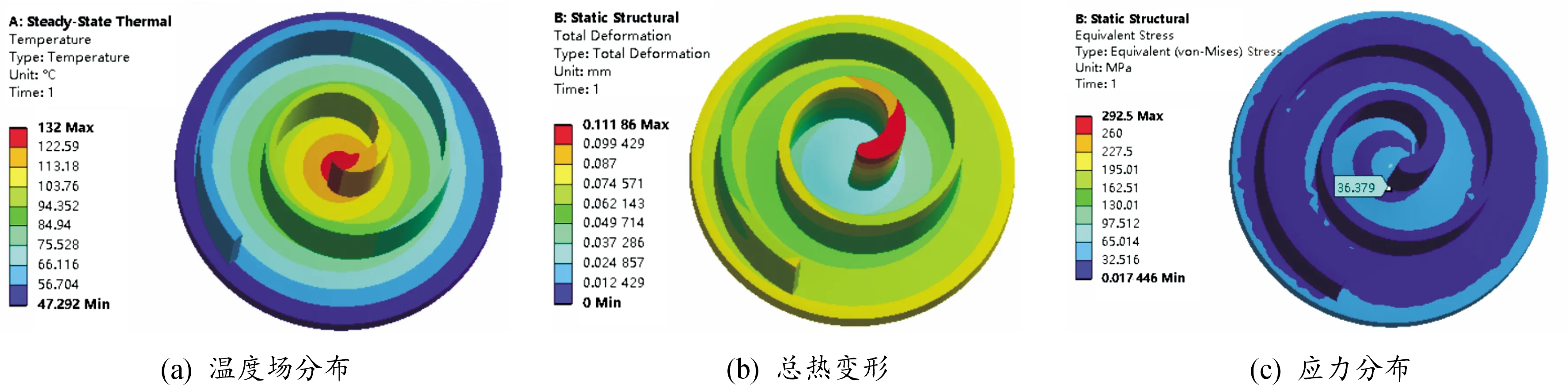
图3 线性温度场下的热分析
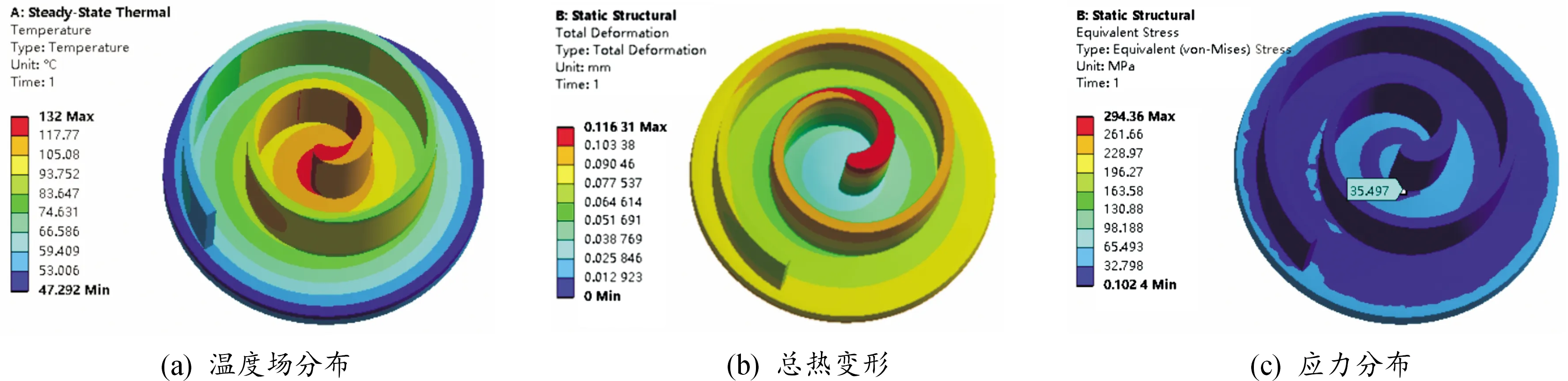
图4 流场温度场下的热分析
为了更直观地观察涡旋齿的变形情况,以涡旋齿齿头顶端为原点,型线弧长为x坐标,变形量为y坐标,绘制涡旋齿顶部变形曲线和以涡旋齿齿头与端板接触始端为起点,型线弧长为x坐标,应力值为y坐标,绘制涡旋齿与端板接触处的应力分布曲线,分别如图5和图6所示,图中M代表线性温度场下的应力和变形结果,N代表基于流场温度下的应力和变形结果。

图5 涡旋齿顶部变形曲线
图6 涡旋齿与端板接触处的应力分布曲线
通过对比分析,在热变形上,由于分析求解时,在涡旋盘端板上施加了Z方向的约束,两者最大变形均位于齿头部分,但后者最大热变形116.3 μm大于前者111.9 μm。由变形曲线可知,在弧长为0~100 mm范围内,变形量下降速度较快,而后比较平缓,在齿尾处又有所上升,这是因为涡旋齿前端膨胀腔体积随主轴转动变化较大,且由于齿头部分经修正后齿壁较厚,相对于弧长100 mm以后的涡旋齿,温度梯度变化较大,变形量下降速度较快,后因热胀冷缩,齿尾呈现外凸的趋势,局部变形量有所上升。另外,不难发现后者涡旋齿整体变形分布大于前者,这是由于实际情况下膨胀腔腔内温度分布是不均匀造成的,文献[17-21]中对膨胀机内部流场特性展开了数值模拟研究,得到了流场下的温度分布的复杂性和不均匀性,并且文献[16]中已经验证了数值模拟结果相对于性能试验结果的有效性,所以基于流场结果得到的涡旋膨胀机运行参数更符合其实际工况,温度场分布更合理,其造成的热变形更能有效的模拟真实变形情况;对于热应力,由于在动涡盘端板下部的轴承孔内壁面以及顶部设置了位移约束,所以应力分布表现在轴承孔与端板交界处和涡旋齿与端板接触位置,通过两者热应力的比较可以看出,应力分布趋势大致相同,最大热应力集中在涡旋齿齿头与端板接触部分,且前者61 MPa小于后者69 MPa,在弧长为200~400 mm,两者应力分布差异较大。
3 气体力作用下的应力变形分析
由涡旋膨胀机工作机理可知,在吸气结束时,膨胀机内部气量最大,涡旋盘所受气体力最大[7],因此本研究中选择主轴转角为吸气结束时的状态进行分析。此状态下,由于涡旋圈数小,此时仅存在一对中心吸气腔、一对压缩腔和一对排气腔。
3.1 气体力载荷设置
3.1.1基于热力学模型的气体力载荷
涡旋膨胀机涡旋盘在运动过程中,较高的气体温度和气体力作用是导致涡旋齿变形的主要因素。而涡旋盘所受的气体作用力是涡旋齿内外壁面的压力所致,且由于不同位置压力分布不同,内外侧存在一定压差,气体径向力作用在内外侧壁面,如图7所示为壁面压力分布示意图。所以气体径向压力载荷可简化为相邻膨胀腔的压力差,作用于内壁表面。
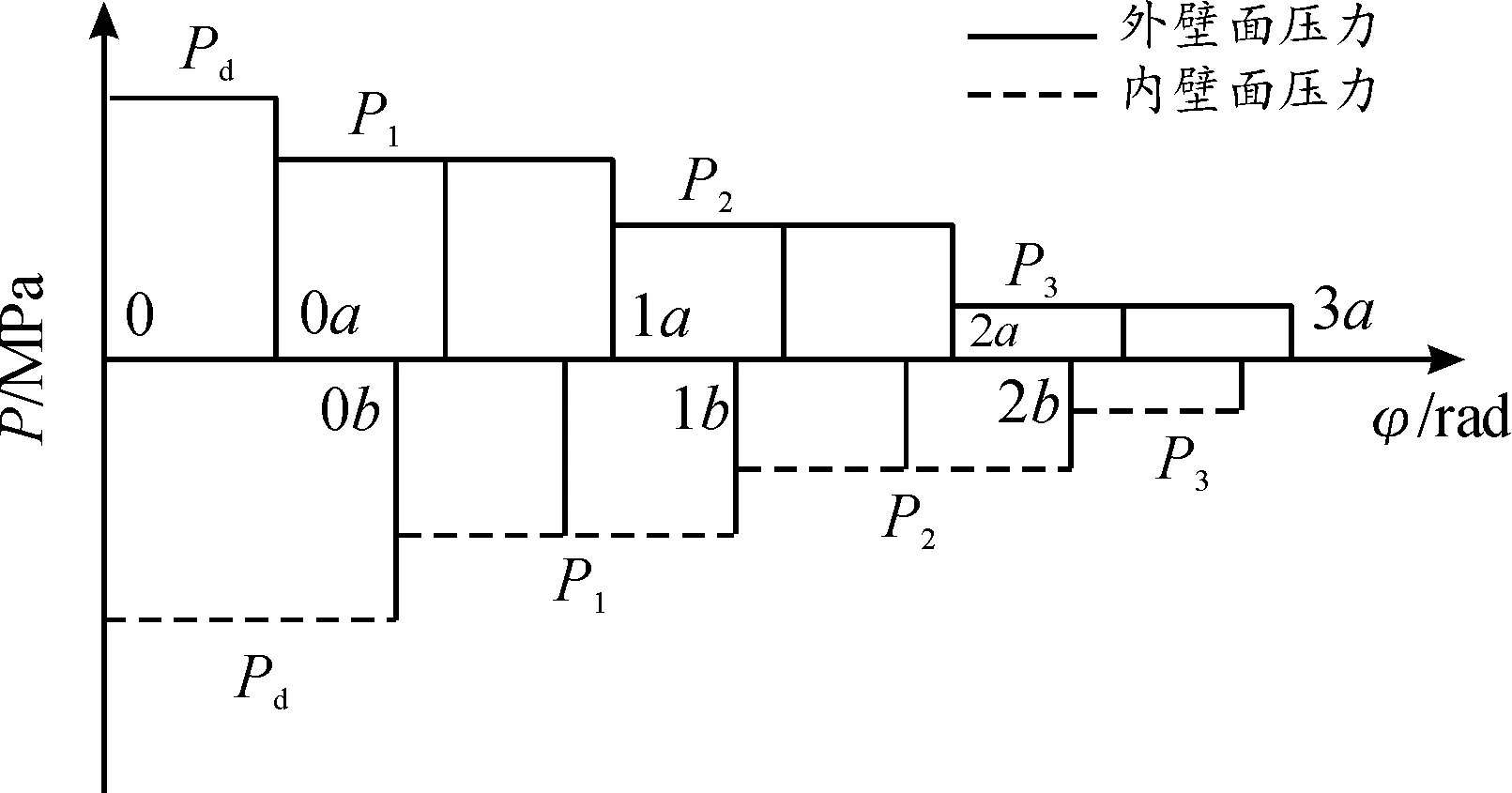
图7 压力分布示意图
而涡旋盘所受的气体作用力的大小受膨胀机膨胀腔容积大小的影响,膨胀腔容积大小又随主轴转角的变化而变化,呈现周期性、时变性的变化特点。通过文献可知涡旋膨胀机膨胀腔容积计算公式为:
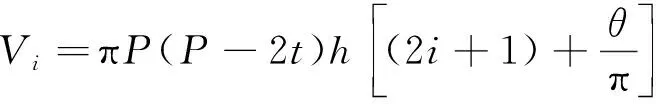
(7)
式中:Vi为各膨胀腔容积编号;P为涡旋体节距;t为涡旋齿厚;h为涡旋齿高。
假设膨胀过程是绝热进行的,那么通过气体绝热过程的P-V关系式可以求出第i个膨胀腔内的气体压力,P-V关系表达式如下:
(8)
式中:Ps为吸气压力;k为气体等熵指数,取k为4/3;VS为初始容积;Vi为第i个膨胀腔的容积。
通过上式气体压力计算公式可得中心进气腔理论计算值为1.1 MPa,膨胀腔理论计算值为0.584 MPa,排气腔腔理论计算值为0.3 MPa。
3.1.2基于流场的气体力载荷
测定流场数值模拟下各膨胀腔的压力平均值,形成如表3所示的压力载荷对照表,再在ANSYS中对涡旋盘施加Fluent仿真结果下的各腔压力值,将其自动转换到对应的各节点上。
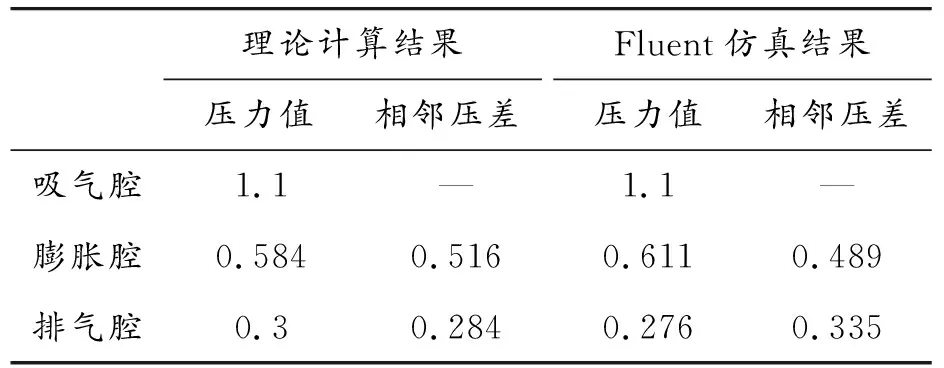
表3 压力载荷结果对照表 MPa
3.2 气体力作用下的模拟结果分析
对动涡旋盘分别施加基于热力学模型计算得到气体力载荷和基于流场Fluent仿真结果得到气体力载荷,应力和变形结果云图分别如图8和图9所示。拾取与温度场相同的顶部形变路径和底部应力分布路径,得到气体力作用下的涡旋齿顶部变形曲线如图10所示和底部应力分布曲线如图11所示,图中P代表基于热力学模型下的应力和变形结果,Q代表基于流场气体力下的应力和变形结果。
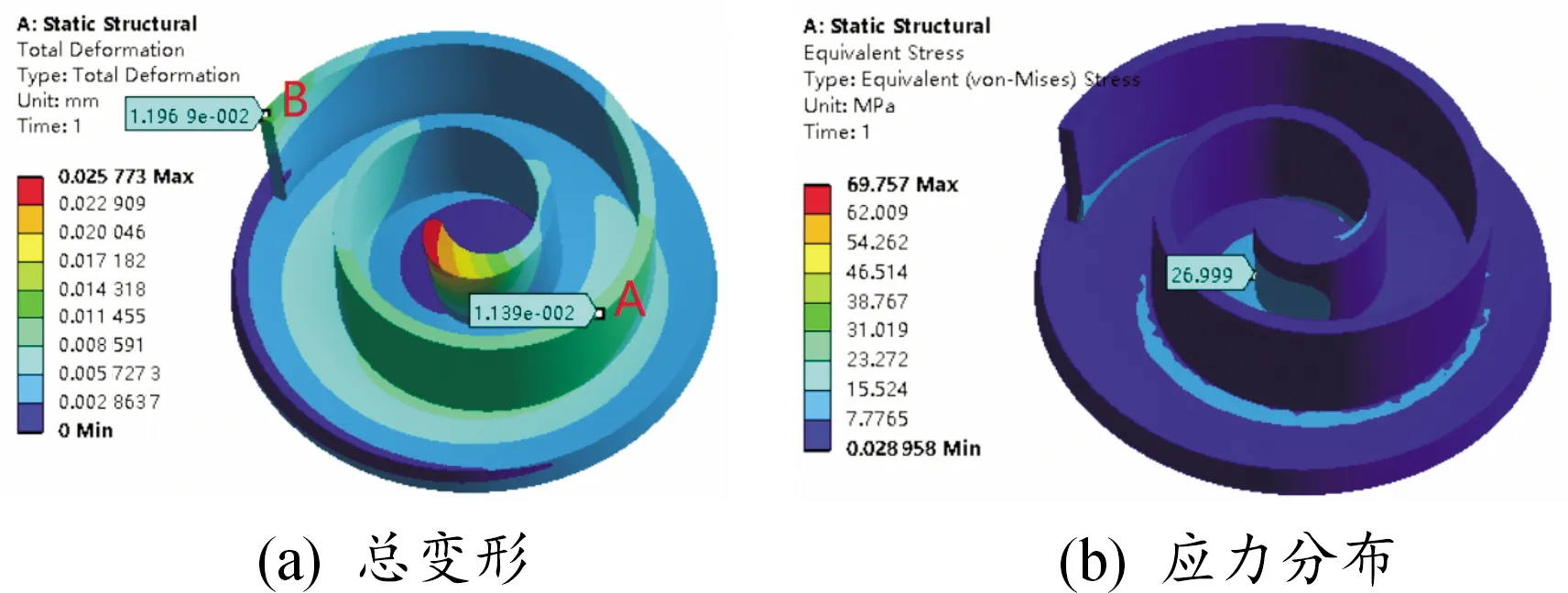
图8 热力学模型下的气体力应力变形分析
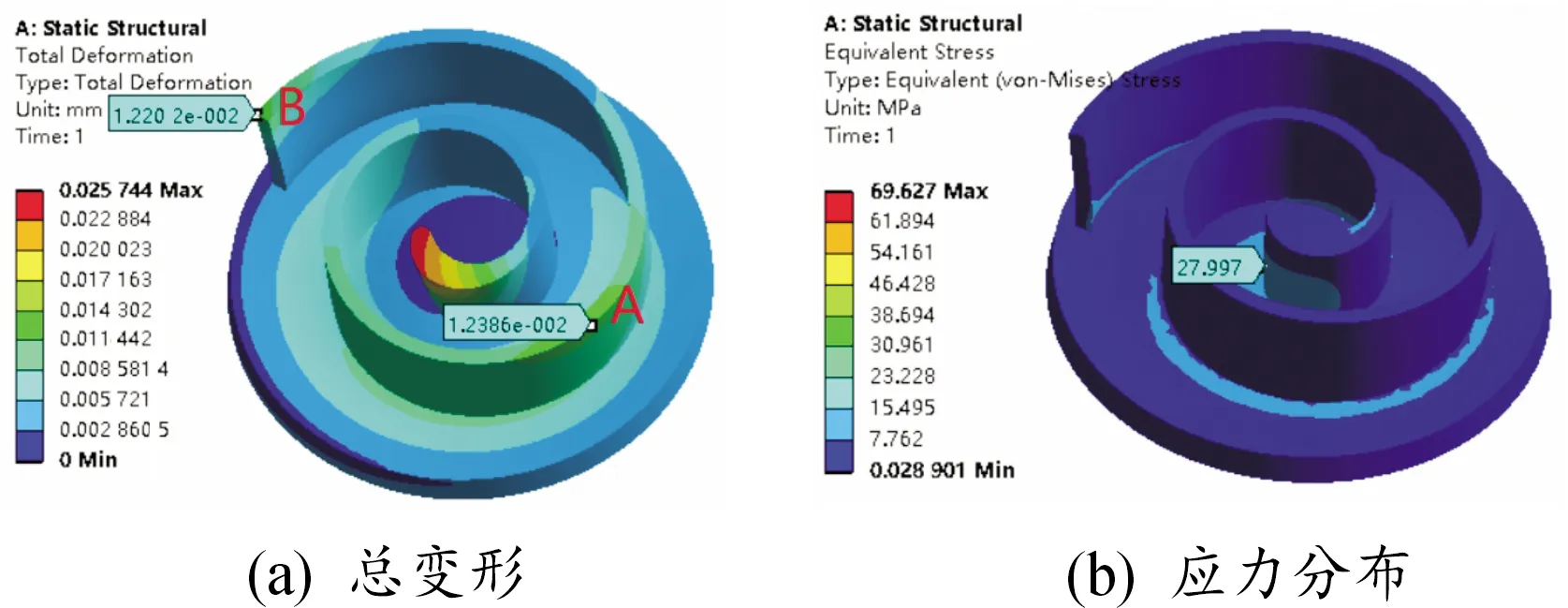
图9 Fluent仿真结果下的气体力应力变形分析
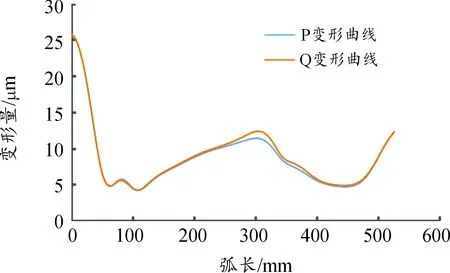
图10 气体力作用下的涡旋齿顶部变形曲线

图11 气体力作用下的涡旋齿与端板接触处的应力分布曲线
通过对比分析发现,2种气体力作用下的最大变形均在涡旋齿齿头处,而且变形量降速很快,此后有所减缓,且都有沿外圈减小的趋势;与温度场作用下的变形曲线对比可知,气体力作用下的变形远小于热载荷作用下的变形;此外,云图上的B点和变形曲线末端的变化都展现了变形量有所增大的趋势,这是由于涡旋齿Z轴方向被约束,相对于齿高来说,其齿厚较薄,在载荷作用下产生了类似悬臂梁的效果,应力产生集中,因此形变也相应较大;两者整体的应力和形变分布基本一致,验证了计算的正确性;两者膨胀腔A处的变形均高于两侧,对应了曲线中弧长为280~320 mm中的一点,且在这个范围内,基于流场气体力下的涡旋盘形变值高于基于热力学模型下气体力造成的形变值,整个形变曲线呈现不同幅度的波动,分析可知是由于齿壁内外侧存在压力差造成的,且相邻膨胀腔压差值越大,其波动幅度越大,通过表3可知Fluent仿真结果下的相邻膨胀腔的压力差高于热力学模型计算下的相邻膨胀腔压力差,故基于流场结果下的点A处的形变值高于热力学模型计算下的点A处的形变值。另外,基于流场下的点A处的形变值和点B处的应力值均略高于基于热力学模型下的A处形变值和B处应力值,一是因为气体力分布不均,二是因为膨胀机实际运行下,情况更复杂,会受到环境、设备、摩擦等因素的影响从而有所变化。
4 耦合作用下的应力变形分析
由于基于热力学模型下和基于流场下的气体力作用下的应力变形情况基本相同,故选取其中之一分别与2种形式下的温度场进行耦合分析。图12为线性温度场与流场下气体力的耦合分析结果;图13为流场下的温度场和流场下的气体力的耦合分析结果;图14为耦合作用下的涡旋齿顶部变形曲线;图15为耦合作用下的涡旋齿与端板接触处的应力分布曲线,图中S代表线性温度场和流场下气体力耦合的结果,R代表流场下的温度场和流场下气体力的耦合结果。

图12 线性温度场与流场下气体力的耦合结果
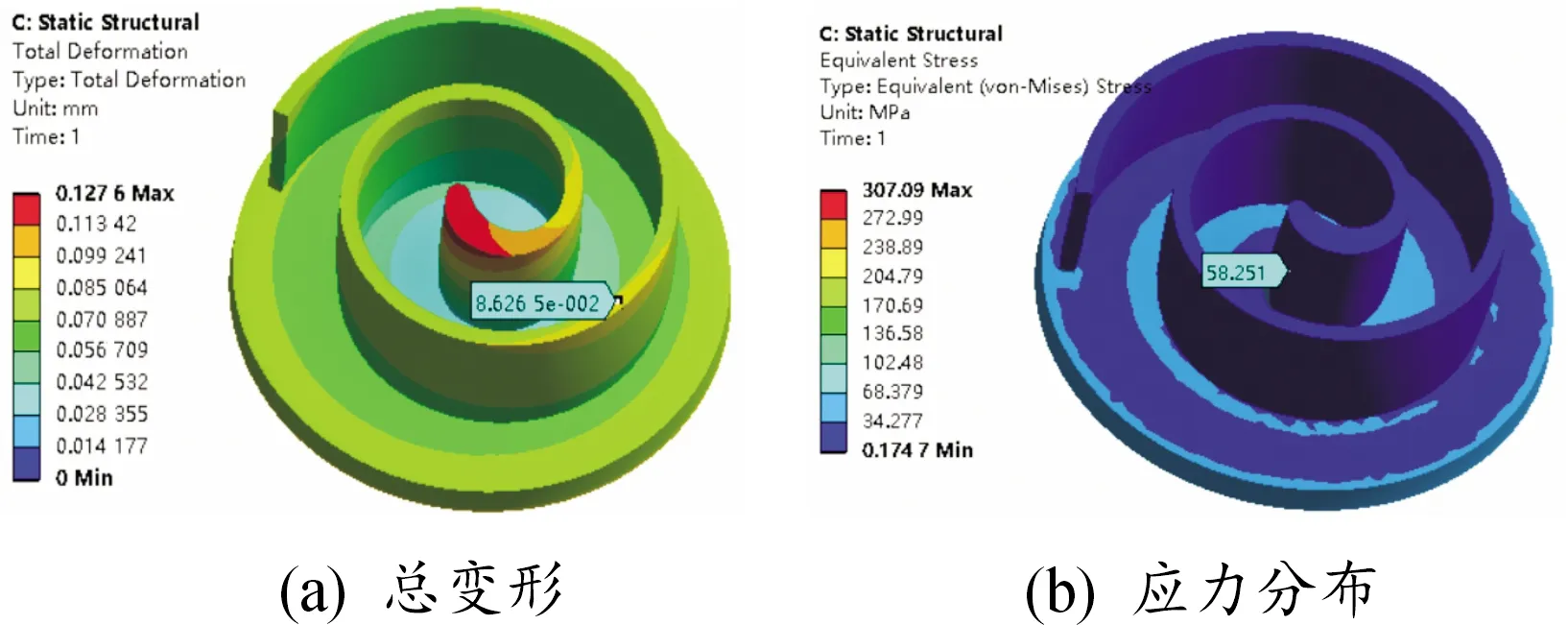
图13 流场下的温度场和气体力的耦合结果
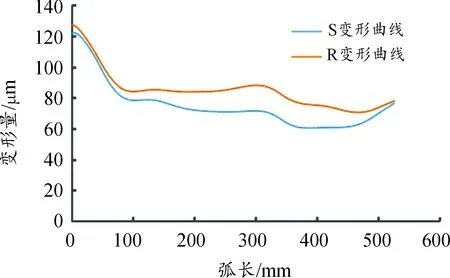
图14 耦合作用下的涡旋齿顶部变形曲线
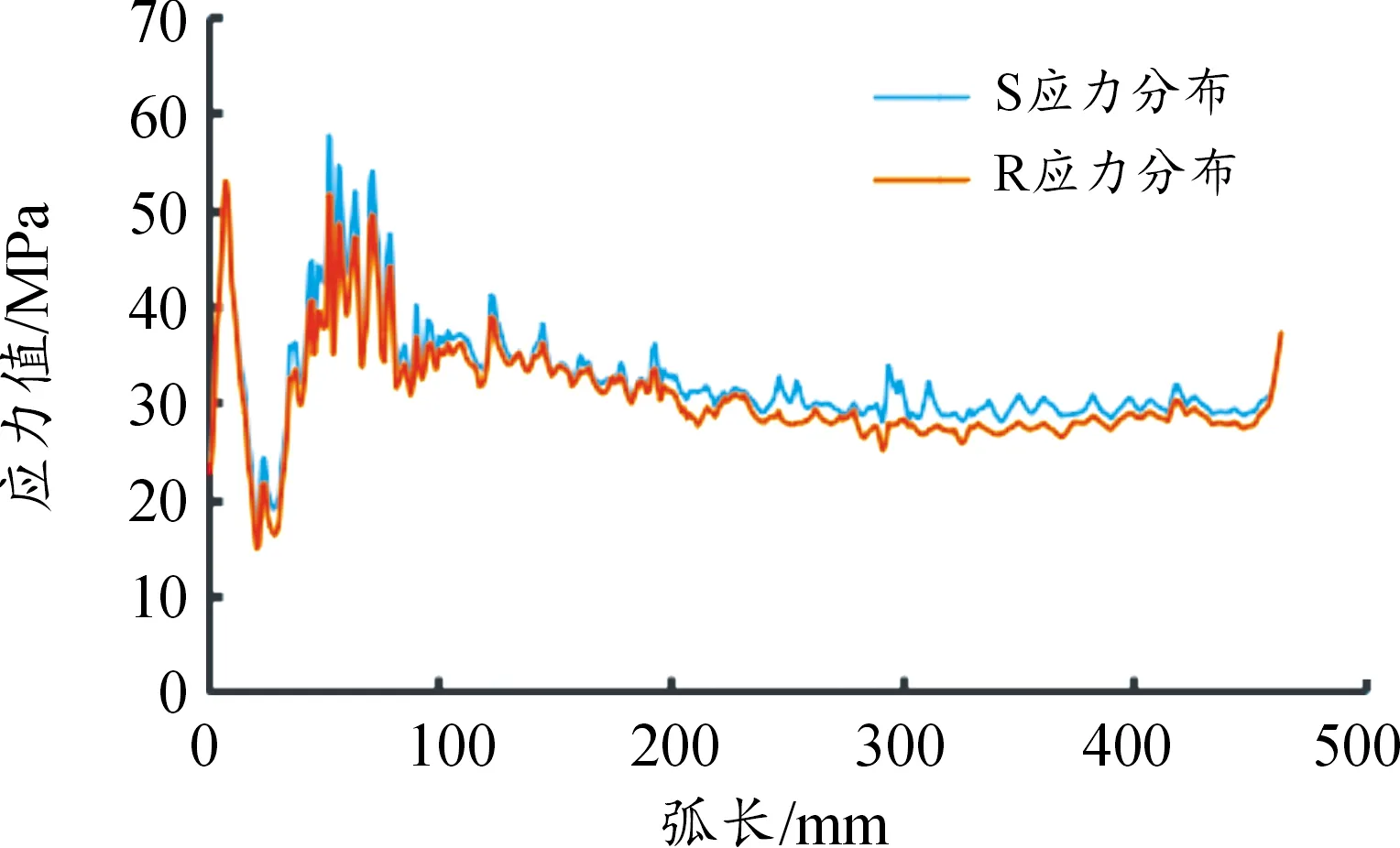
图15 耦合作用下的涡旋齿与端板接触处的应力分布
通过耦合分析可知,耦合作用下的涡旋盘涡旋齿变形更严重,最大变形量分别为125 μm和127 μm,大于任何一个载荷单独施加下的形变量,且不是单独施加结果下的简单线性叠加,其中热载荷影响较大;耦合作用下的变形趋势与气体力、温度载荷单独作用施加下的变形趋势相似,都呈现向外圈逐渐减小的趋势,最大变形发生在涡旋齿中心齿头部分,齿顶位置变形更突出;涡旋齿最大应力集中在涡旋齿与端板接触的位置;耦合过后的变形曲线和应力分布曲线较单独施加作用下的结果更稳定,波动幅度较小,说明温度场与气体力之间在共同作用时相互之间存在一定影响;线性温度场和基于流场下的气体力耦合后,涡旋盘变形量低于流场下的温度场和流场下的气体力耦合后的变形量,而应力值分布却略大于后者,这是因为经流场分析得到的温度场和气体压力更符合涡旋膨胀机实际工况,分布更合理。
5 结论
1) 在单独施加温度和单独施加气体力下,温度载荷引起的应力和变形远大于气体力引起的应力和变形,所以可以得出温度载荷是导致涡旋齿变形的主要原因,降低涡旋膨胀机的工作温度能有效减少变形量和热应力。
2) 基于线性分布的温度热载荷和基于流场得到的热载荷在某些特殊转动位置下造成的热变形和热应力相差不大,可作为一种备选施加方案,但流场下的热载荷分布更合理,更符合实际。
3) 理论计算得到的气体力载荷和基于流场得到的气体力载荷所得的变形效果很接近,可互相作为一种验证方式。
4) 由于各工作腔内气体压力不同,相邻膨胀腔存在压差,压差越大,波动越大,形变量越大,在与吸气腔相连的第一膨胀腔形变最明显。
5) 各载荷单独施加作用下和耦合作用下的最大变形均位于涡旋齿齿头顶部,所受应力集中于涡旋齿和涡旋端板连接处以及轴承孔与端板的交界处,应力和变形分布由涡旋齿中心向外围逐渐减小。且耦合作用下的变形值不是单独作用下变形值的线性叠加,耦合下的值大于单独施加得到的值。

