基于蒙特卡罗模拟的离子导体热力学与动力学特性

刘金平，蒲博伟，邹喆乂，李铭清，丁昱清，任 元，罗亚桥，李 杰，李亚捷，王 达，何 冰，施思齐,5,6

（1上海大学材料科学与工程学院，上海 200444；2湘潭大学材料科学与工程学院，湖南 湘潭 411105；3加州大学欧文分校物理与天文系，美国 加州 92697；4上海大学计算机工程与科学学院；5上海大学材料基因组工程研究院，上海 200444；6之江实验室，浙江 杭州 311100）

明确离子导体的离子输运与相变特性是制备新型全固态电池、电化学转换器件等离子型器件的关键[1-3]。离子导体的典型结构包括在输运网络中嵌入或迁移实现电荷储存与传输的迁移离子以及构建离子输运网络的仅原点附近振动的骨架离子[4-5]。高离子电导率的超离子导体的筛选过程通常采用高通量计算方法[如几何分析方法(crystal structure analysis by voronoi decomposition，CAVD)[6-7]、配位成键理论(bond valence site energy，BVSE)[8-9]等]分析骨架离子中的离子输运网络。同时，借助基于牛顿力学的分子动力学(molecular dynamics，MD)模拟[10]或基于离子迁移实验的动力学蒙特卡罗(kinetic Monte Carlo，KMC)模拟[11]分析迁移离子的输运特性(例如离子电导率[12-13]、扩散系数[8,10,14]等)。借助群论、巨正则蒙特卡罗(grand canonical Monte Carlo，GCMC)模拟等热力学模拟手段研究离子导体的结构演化。分子动力学(MD)模拟作为典型的动力学模拟手段因其计算精度高、模拟分子运动过程清晰等优势，在离子扩散模式分析[15]及晶体生长模拟[16-17]等方面具有广泛应用。然而其内禀缺陷限制了MD适用于更广泛的应用场景。例如，第一性原理分子动力学模拟计算速度较慢、难以应用到较大体系的快速模拟；而平均场分子动力学模拟不易获取其所需的高精度势函数。因此，具有类似计算功能的KMC 模拟因计算速度快、扩展性强而被广泛应用于评估离子导体的离子输运特性。表1对几种典型的MD模拟与MC模拟[18-20]进行了对比，尽管两者的应用范围存在众多交叠，但基于计算原理的差异性，MC 模拟具有更广泛的时空尺度。此外，在热力学模拟领域(如相图计算[21]、电压平台计算等)，相较于第一性原理相图计算[22]以及空间群分解[23]等模拟手段，MC 模拟同样在计算速度与适用性等方面存在巨大优势。

表1 MC模拟与MD模拟的对比[18-20,28-32]Table 1 Comparison between MC simulation and MD simulation[18-20,28-32]

目前，MC 模拟还存在计算精度不高、计算过程依赖于较多的输入参数、蒙特卡罗时间与真实时间之间存在差异、无法捕捉细小的离子振动等不足之处。为促进MC模拟的发展与应用，本文介绍了其发展历史，提炼出MC模拟的基本模拟范式与具体计算步骤，以期为科研工作者开展离子导体的相关物化特性研究铺平道路。本研究给出了一套具体的KMC 计算程序，并对石榴石型固态电解质的离子输运特性进行了分析，供读者参考。为清晰地了解MC模拟的适用情形，本文就几种典型的离子导体材料(锂离子电池正极材料[24-25]、负极材料[26]以及固态电解质材料[27]等)介绍了MC 模拟的计算结果。最后，本文对当前MC模拟所面临的挑战以及未来可能突破的方向进行了总结，期待该方法的进一步发展。

1 蒙特卡罗模拟方法基础

1.1 蒙特卡罗模拟方法

MC 模拟作为一种基于随机抽样统计的模拟手段[33]，由美国数学家冯·诺伊曼等[28]于20世纪40年代在美国的“曼哈顿计划”中提出。到20世纪50年代，进一步提出了MC模拟中可适用于大多数物理平衡系统的著名算法：Metropolis 算法[34]。20 世纪60 年代，KMC 模拟开始出现。与此同时，混合蒙特卡罗(hybrid Monte Carlo，HMC)采样算法[31]等也得到了广泛地研究。进入21 世纪以来，随着人工智能的快速崛起，蒙特卡罗树搜索算法等更为先进实用的计算方案也得到了快速发展[35-39](图1)。根据研究对象的不同，MC 模拟可分为两类：一类是针对热力学平衡过程中非时间关联性问题的模拟，如常见的GCMC 模拟；另一类是对时间关联的动力学问题的研究，如KMC 模拟。这两种MC 模拟的最终目标都是尽可能地寻找徘徊在某一低势能面附近的结构组态。从原理上讲，GCMC 与KMC之间存在应用场景的重合，即巨正则体系依旧可以进行KMC模拟，反之亦然。多数KMC模拟与热力学MC模拟均可以利用格子气[32,40]模型建模，故而上述多数模拟均属于格子气蒙特卡罗(lattice-gas Monte Carlo，LGMC)模拟。而格子气模型的MC 模拟多属于典型的马尔科夫链(Markov chain)[28,33,41]过程，所以这种MC模拟也可以叫作马尔科夫链蒙特卡罗(Markov chain Monte Carlo，MCMC)。这几种模拟手段之间的关系可以通过图3(e)所示的维恩图表示。基于上述几种MC 模拟的计算过程大多相似，本文将在格子气MC模拟的介绍中对体系描述、体系演变及新体系接受概率等细节问题进行重点介绍。

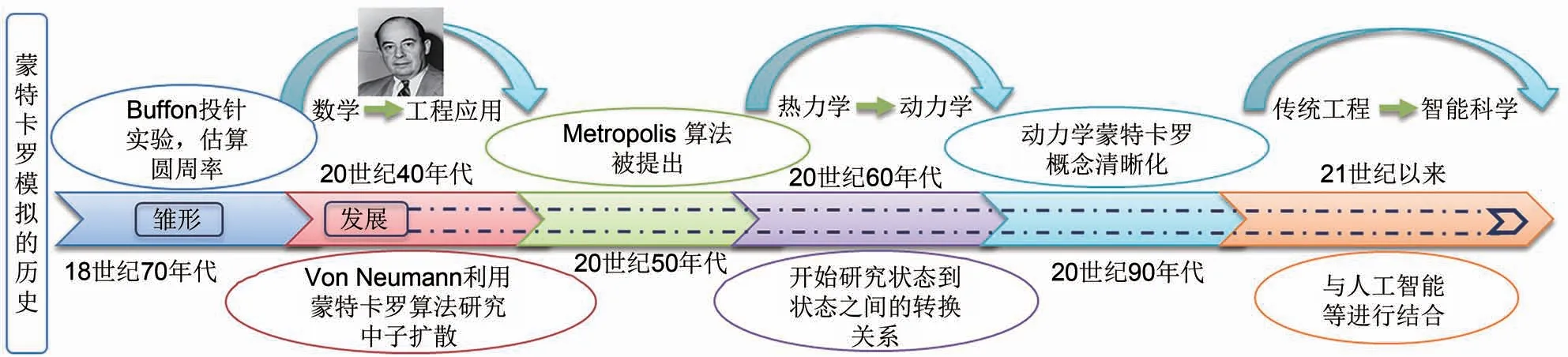
图1 蒙特卡罗模拟的发展Fig.1 The development of Monte Carlo simulation

1.2 蒙特卡罗模拟过程

GCMC[42-43]模拟作为一种适用于巨正则系综限制下经典的热力学MC模拟，被广泛应用于电化学储能材料的合成、多孔吸附等过程的研究[44]。在电化学储能材料计算领域，GCMC常用于模拟石墨等碳基嵌锂材料的结构特征。在模拟过程中，随机选择几种基本的离子运动模式(比如置换、插入、脱出)，并对相应离子运动模式发生的概率进行计算[45]，一般可以通过式(2)所示的计算模式求得。值得指出的是，式中的能量变化不仅可以使用体系的始末态能量表示，也可以使用过渡态能量表示[46]。对于忽略动力学特性的热力学模拟，仅考虑简单的始末态能量是常见的。作为GCMC 模拟适用情形的补充，KMC 模拟则可以很好地描述离子导体结构演变的动力学过程。KMC 模拟的研究最早可以追溯到20 世纪60 年代对辐射损伤退火问题的模拟。目前，KMC 在表面吸附、离子扩散、晶体生长等领域得到了迅速发展和应用[28]。由于模拟机理不同，KMC 相对于分子动力学(MD)模拟可以对更大系统的动态演化过程给出更长时间的模拟[34,47]。离子导体中迁移离子的成功迁移并不频繁，其状态转变会经历长时间的“尝试”，只有极少的“尝试”会成功。KMC 模拟不考虑尝试过程只关注可以演变成功的状态，这种状态到状态的转变不受原子振动的限制，不局限于对每个原子(离子)的计算，因此可以实现更长时间尺度的模拟[48]。同时，KMC的离散化思想更适合对微观离散体系进行模拟分析，这也使得离散化模型的搭建在KMC 模拟中占据着十分重要的地位[49]。LGMC[32,50]模拟即为一种典型的离散化处理方式。

GCMC 模拟与KMC 模拟均可以借鉴格子气模型而发展成为一种特殊的LGMC模拟来描述离子在材料体系中的扩散与占位情况。在格子气模型的搭建过程中，时间与空间被分割，按照离子之间的相互作用以及迁移、翻转规则，将模拟体系简化成一系列固定的空间格点与可迁移或翻转的离子。图2展示了几种典型格子气模型的示意图。该模型中，离子位于格点上，沿着边运动，离子与离子之间存在相互作用(比如吸引或者排斥作用)。Ising 模型[18]、渗流模型[51]等均是对格子气模型的某种处理与变形。

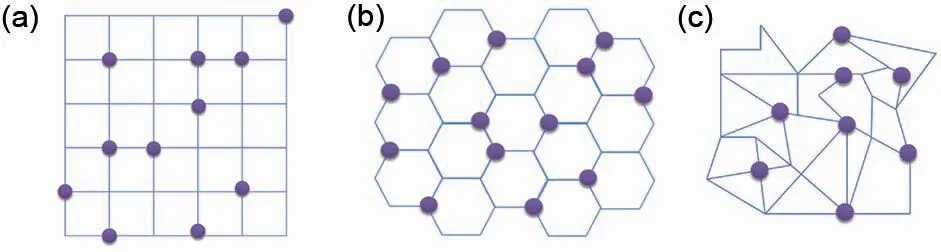
图2 MC模拟中常见的几种二维格子气模型：(a)二维正方格子气模型；(b)二维六边格子气模型；(c)二维随机格子气模型(紫色的球代表格点上的离子)Fig.2 Several two-dimensional lattice-gas model which used in MC simulation commonly:(a)twodimensional square lattice-gas model;(b)twodimensional hexagonal lattice-gas model;(c)random lattice-gas model(The purple spheres represent the ions at the lattice sites)

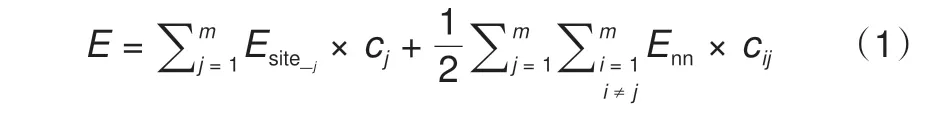
式中，m为总的位点数目；Esite_j为第j个位点被占据所引起的能量变化；Enn为最近邻离子间的相互作用能；cij和cj为前置系数(其值取决于结构中离子的排布状态)。如果位点“j”被占据，则cj= 1，反之cj= 0。如果位点“j”和位点“i”同时被占据，并且它们互为最近邻位点，则cij= 1，反之cij= 0。另外，由Metropolis 等[55]提出的系统演变概率计算公式具有精度较高、可有效避免结构在演变过程中进入局域能量极小值等优点，所以在MC模拟中得到广泛应用(利用此算法的MC模拟也可以叫做Metropolis Monte Carlo，MTMC)。依照此算法，组态a到组态b的演变概率(Pa→b)为

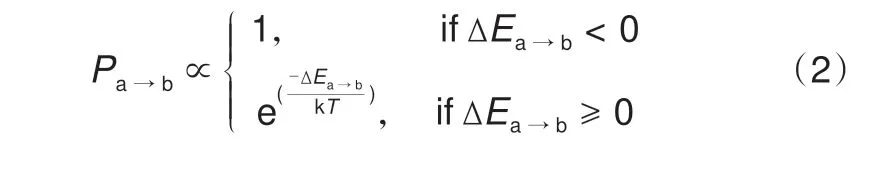
式中，k为玻尔兹曼常数；T为温度，ΔEa→b为系统从组态a 演变到组态b 的能量变化。ΔEa→b计算公式如下

式中，Ea(Eb)为组态a(b)的能量，值得指出的是，ΔEa→b在动力学模拟中也会考虑到过渡态，如迁移能垒的引入等。仅依托于上述内容来计算离子的扩散系数、离子的迁移率等时间相关量是困难的。为了进一步描述材料结构随时间的一系列演变过程进而计算相邻组态之间的时间关联性，常常通过数学近似的方式获得真实的时间步长[20,46]

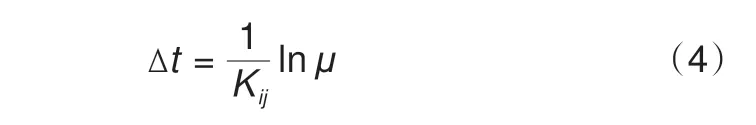
式中，Kij表示“总迁移概率”；μ是随机数[μ∈(0,1)]。由于总概率的计算十分耗时，而在MC模拟过程中一个蒙特卡罗步(MCS)内的离子迁移可认为是同步发生的，所以采用MCS 取代真实时间是一种有效的简化计算方案[56]。这种简化已在传统的热力学计算中被广泛采用。对于MC理论在材料学中的应用，其基本思想是将时-空尺度进行分离，因而其主要用于模拟有序系统，很难应用于无定形系统。对于MC 模拟中相关名词的概念与定义在表2进行了总结。

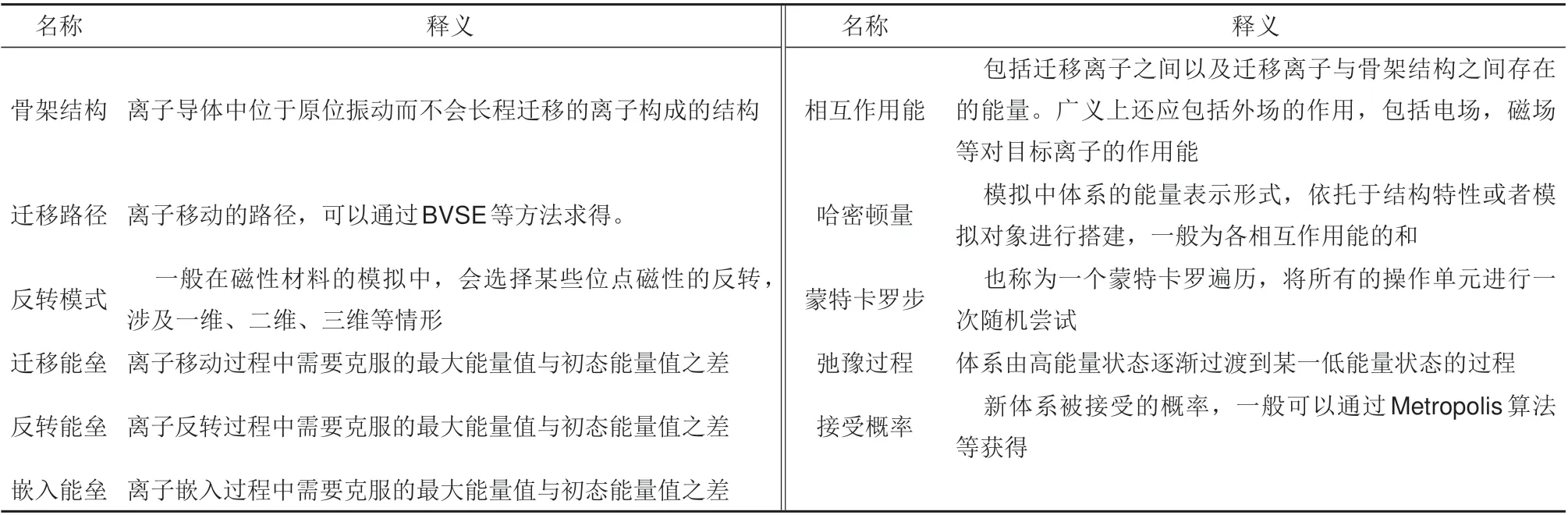
表2 MC模拟中的常用概念Table 2 Common concepts in MC simulation

2 蒙特卡罗模拟的计算范式归纳与示例

MC 模拟已被应用到众多领域，但是如何提高其模拟精度与效率一直是众多科研工作者的重要研究方向[57]。为了清晰了解蒙特卡罗模拟的计算过程，此章节就其计算流程和步骤进行了总结与提炼。一般来说，模型的搭建应尽可能地复现材料的结构特征，比如通过几何分析方式或BVSE来分析材料框架以及离子传输路径，通过格子气模型分析常见的晶态离子导体，通过Ising 模型来分析磁性材料等。此外，合适的模型描述也是决定相关模拟精度的关键。通常研究者会通过对模型能量(如内能)的计算，进而以能量的变化来确定演变方向以及对应构型出现的概率[56-59]。然而，目前还没有一个完美的计算方案可以准确地计算材料构型转变过程中的能量变化。为此，众多科研工作者作了许多努力。比如Arriazu等[45]定义了如图3(a)所示的晶格气体模型，考虑了层内Li离子、层间Li离子以及Li离子与骨架结构的相互作用能，利用GCMC 模拟了Li离子在石墨中的插层过程。在模拟中，作者采用一种纯静态的能量计算模式，即只根据系统的总能来确定此构型出现的概率。因其不考虑过渡态能量，所以该模拟方法在动力学模拟中是不够精确的。对于固定的迁移或反转，激活能垒更能准确反映其能量的变化，因此Ven 等[46]提出了如图3(b)所示的离子迁移能垒。为避免因离子往返迁移能垒不同而造成的计算困难，其引入了一个动力学解析的激活势垒(ΔEKRA)作为能垒的近似，同时还考虑了目标离子周围离子的排布，采用团簇展开的策略，近似计算了离子的迁移概率。然而该近似不仅忽略了离子迁移的方向性，也忽略了多离子迁移模式。迁移模式的选择(材料结构演变途径)是MC 模拟需要解决的第三个关键问题。He 等[15]证明了超离子导体中的离子快速扩散并不像典型固体中那样通过孤立的离子迁移发生，而是通过具有低能量势垒的多离子协同迁移进行[图3(c)～(d)]。实际上，迁移模式的选择是激活能计算的前提，而目前大多数报道都是基于单离子迁移模式，这会造成模拟结果的偏差。综上所述，合理搭建构型，确定体系能量描述并选择合适的构型演变模式，是决定模拟精度的关键。本团队通过模块化的思想提出了MC模拟离子导体材料离子输运特性、相变特性的一般模式。这将大大方便后续开发者用来参考并快速修改，进而扩展MC模拟到具体材料体系。相关模拟的框架主要涵盖以下几个部分(图4)：模拟目标的确定、模拟参数与模型的设定、结构演化方式的选择、转换过程中的能量计算、新结构接受的概率计算以及样本数据的获得。在具体问题中可能还需要增加某些新的模块来处理特殊的需求。基于此流程，本文给出了KMC 计算石榴石结构离子导体离子输运特性的一般范式，如图5(a)所示，其中模型搭建依托于BVSE 与CAVD 的分析结果。模拟过程中的输入输出如表3所示。此外，基于对渗流模拟过程(模型搭建→局域连通性分析→渗流团簇分析→迁移网络统计)的分析，提出了通过KMC模拟搭建渗流模拟初始构型，通过KMC给出的离子迁移模式判断局域通堵，进而对离子输运网络分析的一般范式[图5(b)]。KMC模拟程序框图如图6所示，相应的代码与算例可从代码库https://gitee.com/jinpingliu/pKMC-code.git获得。KMC模拟主程序计算步骤如下。

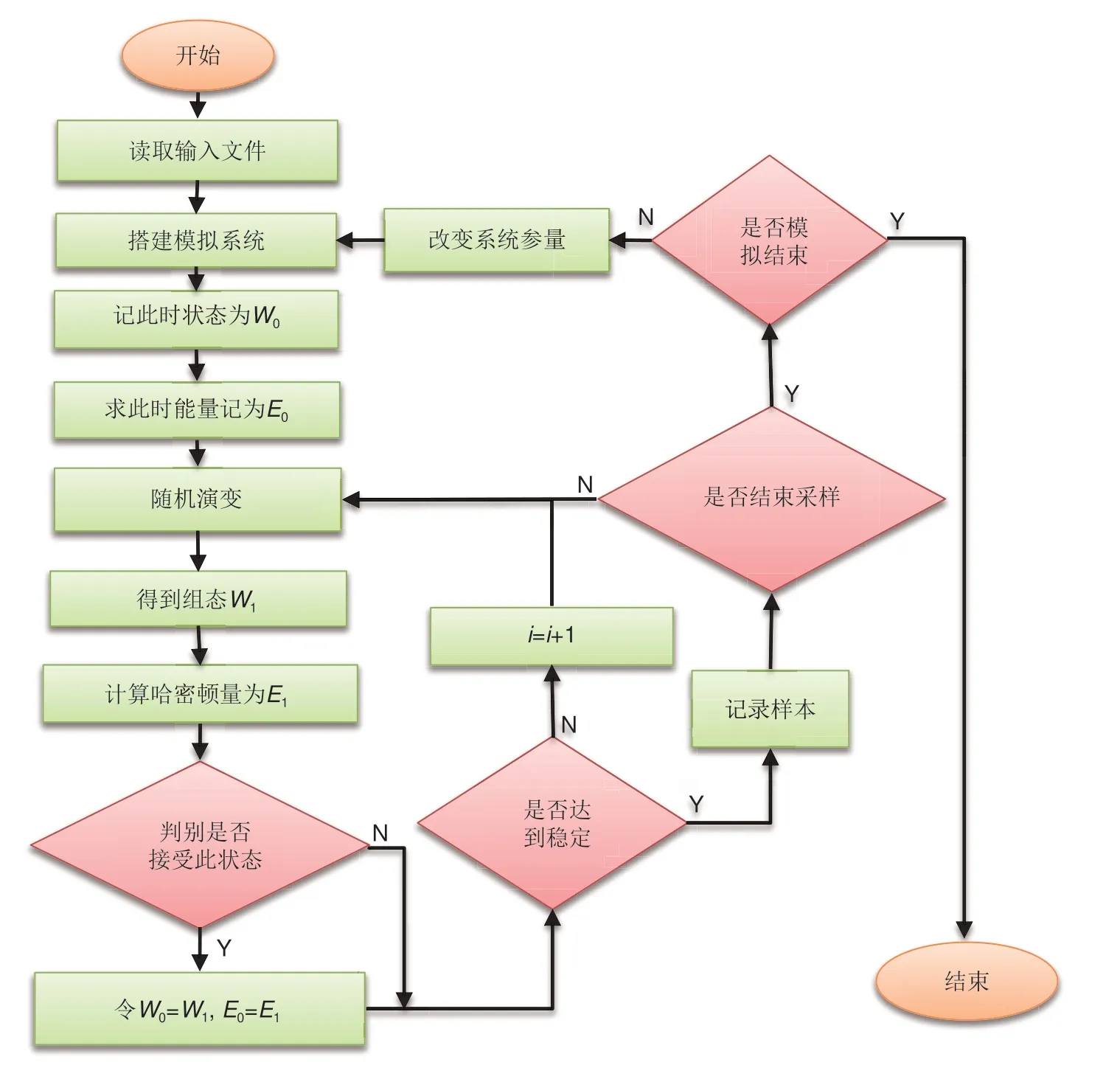
图6 MC模拟在离子导体中的计算程序详细流程框图Fig.6 Flow diagram of MC calculation program in ionic conductor

表3 MC模拟常用的输入与输出Table 3 Some inputs and outputs of MC simulation

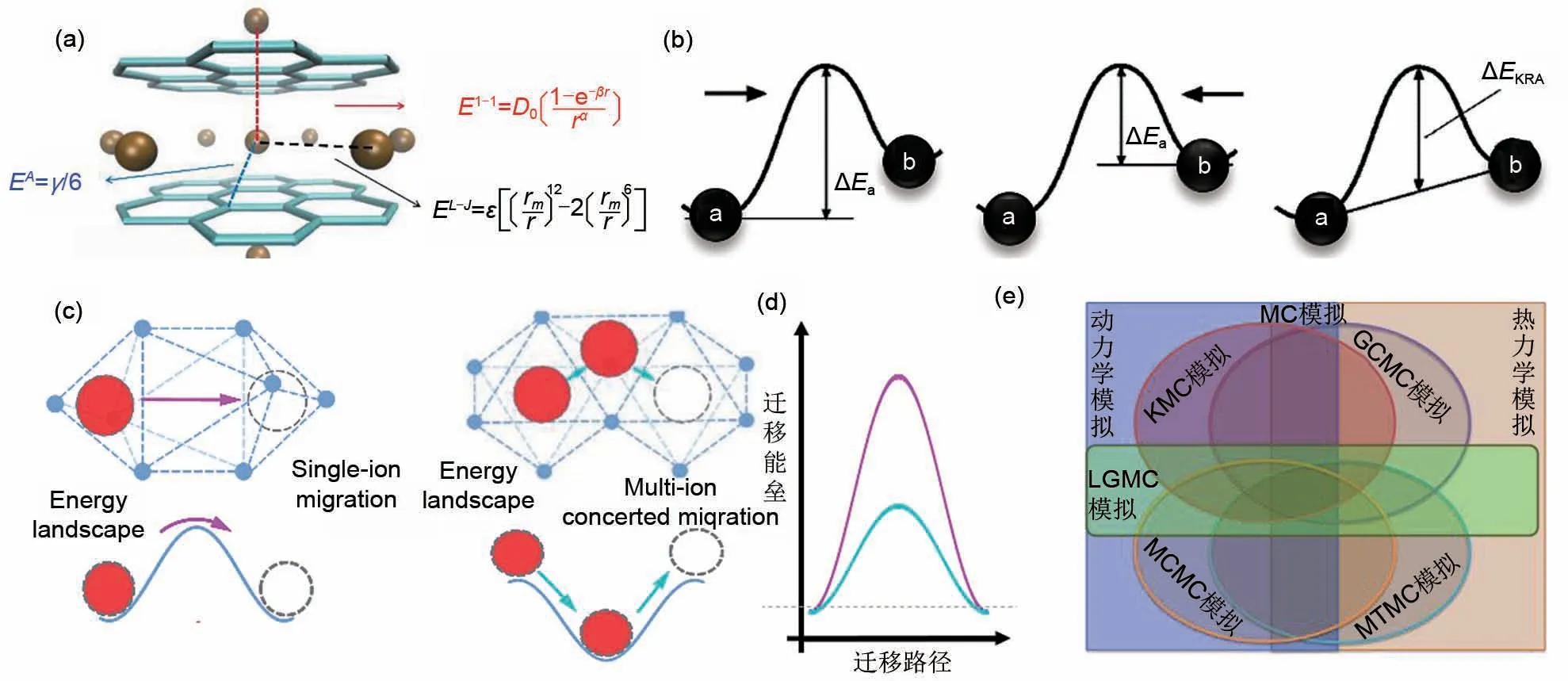
图3 MC模拟中的几种能量近似计算：(a)石墨结构中的锂离子与其他离子之间的相互作用能的计算[45]；(b)迁移离子的迁移过程中所需要克服的迁移能垒示意图[46]；(c)迁移离子的不同迁移模式；(d)不同迁移模式对应的迁移能垒示意图[15]；(e)几种蒙特卡罗模拟之间的关系Fig.3 Approximation of the energy in MC simulation:(a)calculation of the interaction energy between lithium ions and other ions in graphite structure;(b)schematic diagram of the transition barrier during the jump of the migrated ions;(c)different jump modes of migrated ions;(d)different transition barrier of different jump modes;(e)relation diagram between some Monte Carlo simulations

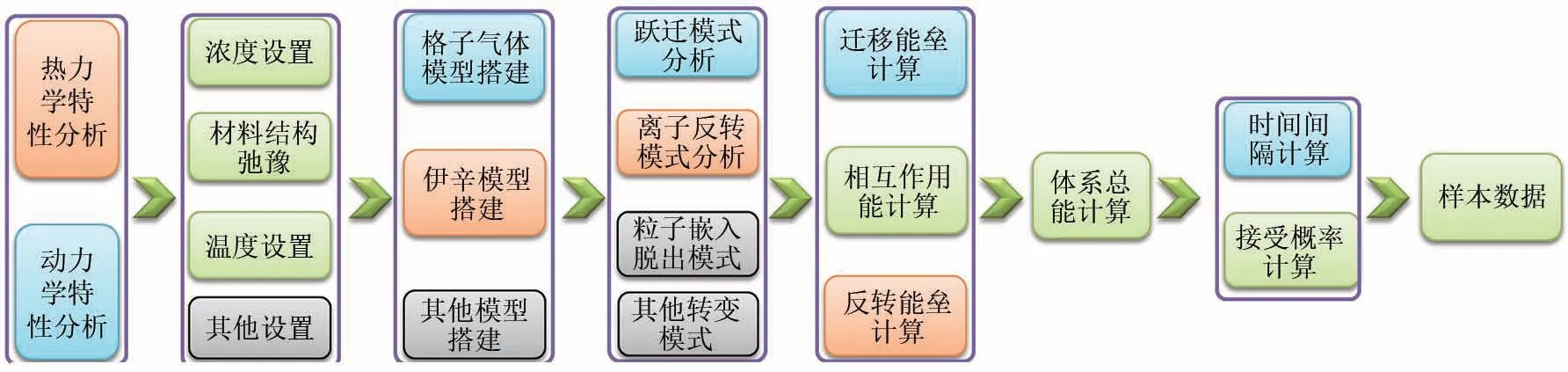
图4 MC模拟的一般步骤，图中列举了MC样本数据的生成过程，蓝色一般为动力学模拟需要的模块，橙色一般为热力学模拟需要的模块，绿色为两者通用模块，灰色是其他模拟中可能存在的模块(此处粒子包含带电离子与其他粒子，具体到离子导体中将用离子描述)Fig.4 General steps of MC simulation,in which listed the calculation process of MC sample data.Blue box is the module required by dynamic simulation,orange box is the module required by thermodynamic simulation,green box is the common module of the both,and gray box represent modules that exist in other simulation(Here,particles include charged ions and other particles,which will be described as ions in ionic conductors)

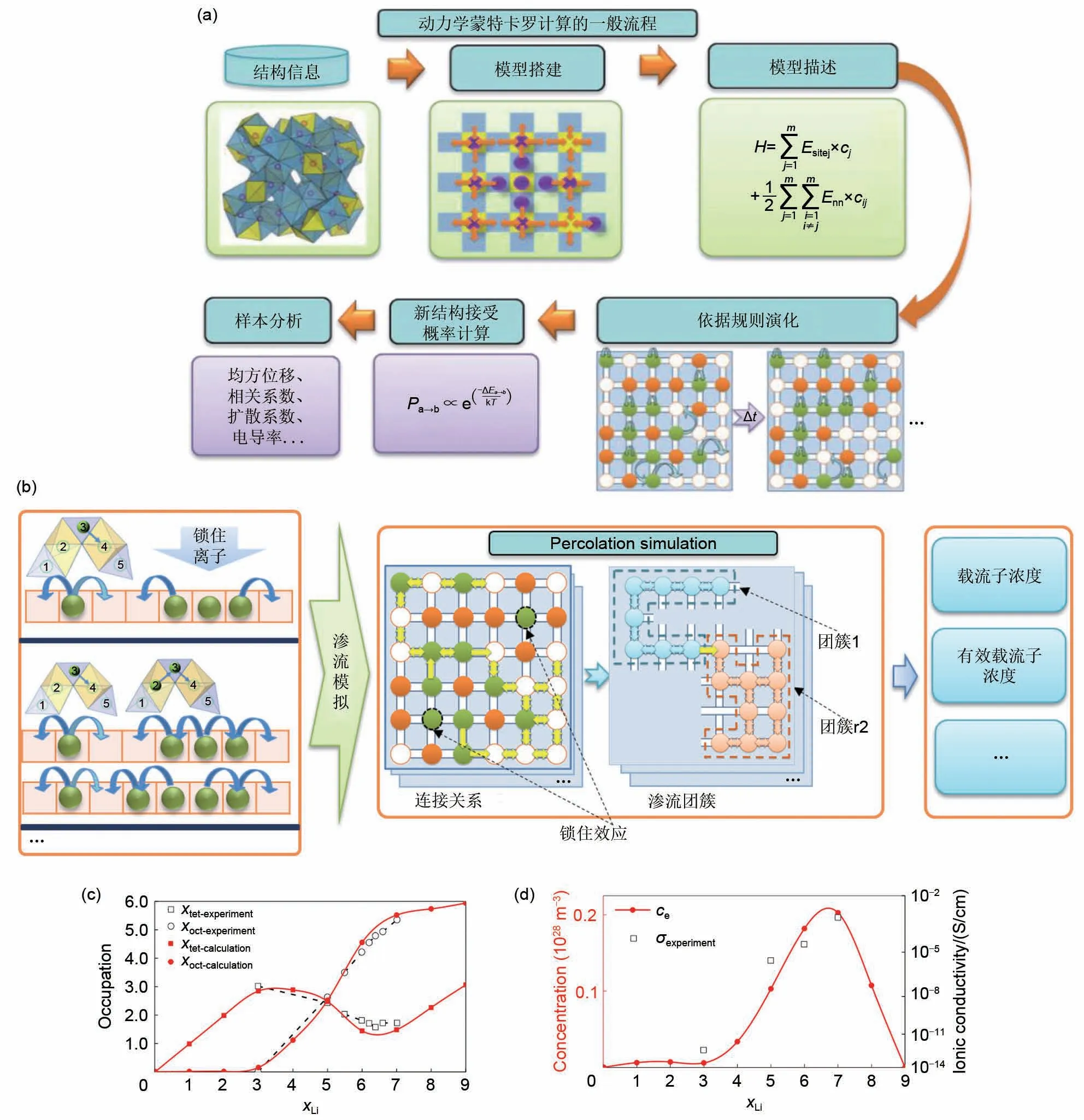
图5 KMC模拟流程与计算案例：(a)KMC对Li7La3Zr2O12(LLZO)的建模与模拟过程示意图(模型构建方式或计算内容依托于具体研究的问题，此处以石榴石结构Li7La3Zr2O12为例，采用BVSE与几何分析方法搭建模型)；(b)KMC模拟与渗流模拟的结合示意图(KMC模拟为渗流模拟提供结构模型、迁移离子排布、离子迁移模式等数据，实现对可达离子，有效载流子浓度等的计算)；(c)通过本KMC模拟程序计算得到LLZO的占据率变化趋势与实验结果[61]的比较；(d)通过本KMC模拟程序计算得到LLZO的电导率预测趋势与实验结果[61]的比较Fig.5 KMC simulation process and calculation cases:(a)schematic diagram of modeling and simulation process of Li7La3Zr2O12(LLZO)by KMC(The model construction method or calculation content depends on specific research questions.Here,the garnet structure Li7La3Zr2O12 is taken as an example,and the model is constructed by BVSE and CAVD method);(b)schematic diagram of KMC simulation combined with percolation simulation(KMC simulation provides the structure model,migrated ion arrangement and ion hop mode for percolation simulation,and percolation simulation is used to calculate accessible ions and effective carriers concentration);(c)the comparison of occupancy calculated by this KMC program with the experimental results;(d)the comparison of ionic conductivity calculated by this KMC program with the experimental results of LLZO

（1）读取外部输入信息，如位点连接关系及位点坐标、迁移能垒、反转(迁移)模式等，根据设定的温度、迁移离子浓度等物理参量搭建初始模拟系统。

（2）记录此时系统的状态，记为W0，计算此时系统的能量，为E0。

阔叶树种，在京城及周边木材市场上进入4季度销路仍然畅通。与针叶原木市场相同的是，在京城以及周边木材市场上经营东北原木的商家普遍认同的仍是俄产木材。这一块阔叶原木由于需求不减，资源品质有保证，价格水平下行机会几乎全无。另外，从俄方进口的北洋阔叶树种原木像榆木、楸木、桦木、杨木、柞木、椴木和水曲柳，不仅需求仍然保持着前两个月的强劲势头，其销售价位也继续坚挺上扬，例如北方市场最认可的水曲柳大径级优质新材售价最强能够冲高到5 000元/m3以上，一般材也就能卖到4 500元/m3左右。

（3）对系统进行随机演变，得到新的组态，记为W1，计算此时系统的能量，记为E1。

（4）对比演变前后组态能量的变化，依据概率P接受新的组态，并更新时间。

（5）重复(3)～(4)过程，直到体系能量基本维持不变，开始记录样本数据。

（6）改变温度，迁移离子浓度等物理参数，重复上述过程，记录多组样本数据，判断是否结束KMC模拟。

（7）对样本数据进行计算，得到迁移率、占据率等物理量。

需要补充的是，上述程序的开发过程依托于对固态电解质材料的计算，其中相关的输入参数使用到了本团队前期开发的BVSE[60]与CAVD 的相关代码[6]。这些输入参数包括骨架结构的离子输运通道，离子在相邻位点之间迁移的平均势垒等。图5(c)～(d)给出了部分计算与实验的结果对比，由图可知，计算得到的LixLa3Zr2O12的离子占据情况与电导率变化均与实验结果相符。

3 蒙特卡罗模拟在离子导体中的应用

多数MC 模拟均可对应到前文对MC 模拟的理论基础与计算范式的介绍与梳理。为了描述MC模拟的应用场景，本节将从离子导体的相变过程、电压平台的变化过程、离子输运特性以及晶体生长动力学特性的分析等方面进行详细的介绍与总结。

3.1 相变分析与电压平台的蒙特卡罗模拟

在锂离子电池中，正极材料的离子输运特性直接决定了电池的容量与循环性能[62]。LiFePO4[63]作为一种被广泛商用的正极材料，在平衡状态下，会自发地分裂出贫锂和富锂两相。如何快速获取相的分离过程十分重要。Xiao 等[59]通过DFT 计算得到KMC 模拟的能垒输入，搭建了如图7(a)所示的模型。模拟结果显示，LiFePO4和FePO4之间形成有序的Li0.5FePO4相[图7(b)]。Hin等[64]通过KMC模拟了LixFePO4橄榄石纳米晶体中锂离子脱出与嵌入动力学特性。结果显示，锂离子嵌入过程中电池电压的变化包含以下几个阶段：①锂离子插入贫锂相导致电池电势下降；②富锂相Li1-βFePO4成核后，电势几乎恒定；③贫锂相完全演变为富锂相以后，电池的电势继续下降[图7(c)～(d)]。除了对LiFePO4不同Li 离子浓度与电压分布关系的计算，Zheng等[65]还对LiNixMn2-xO4/Li 电池系统Ni 掺杂下的电压分布进行了计算。作者首先构建了一个5×5×5的格子气模型，包含1000 个可用位点。在模拟过程中，前500 个MC模拟步作为弛豫过程，接下来的500个模拟步用于热力学量的计算，最终得到电压分布与x值之间的依赖关系，如图7(e)所示。可以看到随着x的增大，4.7 V 电压平台的长度线性增大，4.1 V电压平台的长度线性减小，而总的电池容量则保持不变。当x=0.5时，只观察到4.7 V的电压平台。有序到无序的转变和4.1、4.7 V两个电压平台的分裂都可以归因于锂离子与骨架结构之间的复杂相互作用。不同于上述对单个半电池的模拟，Kar 等[19]通过对两个半电池(LiMn2O4正极和碳负极)进行建模，利用GCMC 模拟给出了温度等参数变化对Li+嵌入与脱出开路电位、电池电流、电池电压、自由能等电池参数的影响。在模拟过程中，当固定温度T、体积V和化学势μ时，每个位置的能量可由式(5)给出

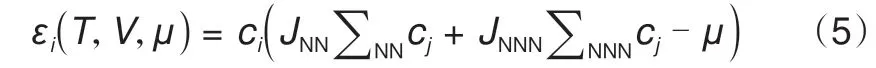
式中，J是锂离子之间的相互作用能，下标NN和NNN 分别表示最近邻和次近邻，如果位点“i”(“j”)被占据，ci(cj)取值为1，否则为0。JNN和JNNN分别为37.5 和25.0 meV。位点占据接受概率可通过式(6)进行描述

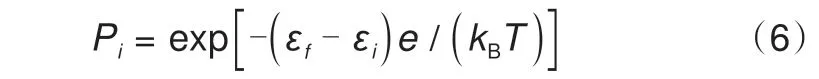
其中，e为电子电荷量。计算得到的开路电位结果如图7(f)所示。这组模拟结果有效地解释了测量开路电位剖面实验中所观察到的迟滞现象。不难发现，上述计算式(5)与(6)来自式(1)与(2)的变形，这种计算模式也被大量的MC模拟所采用。

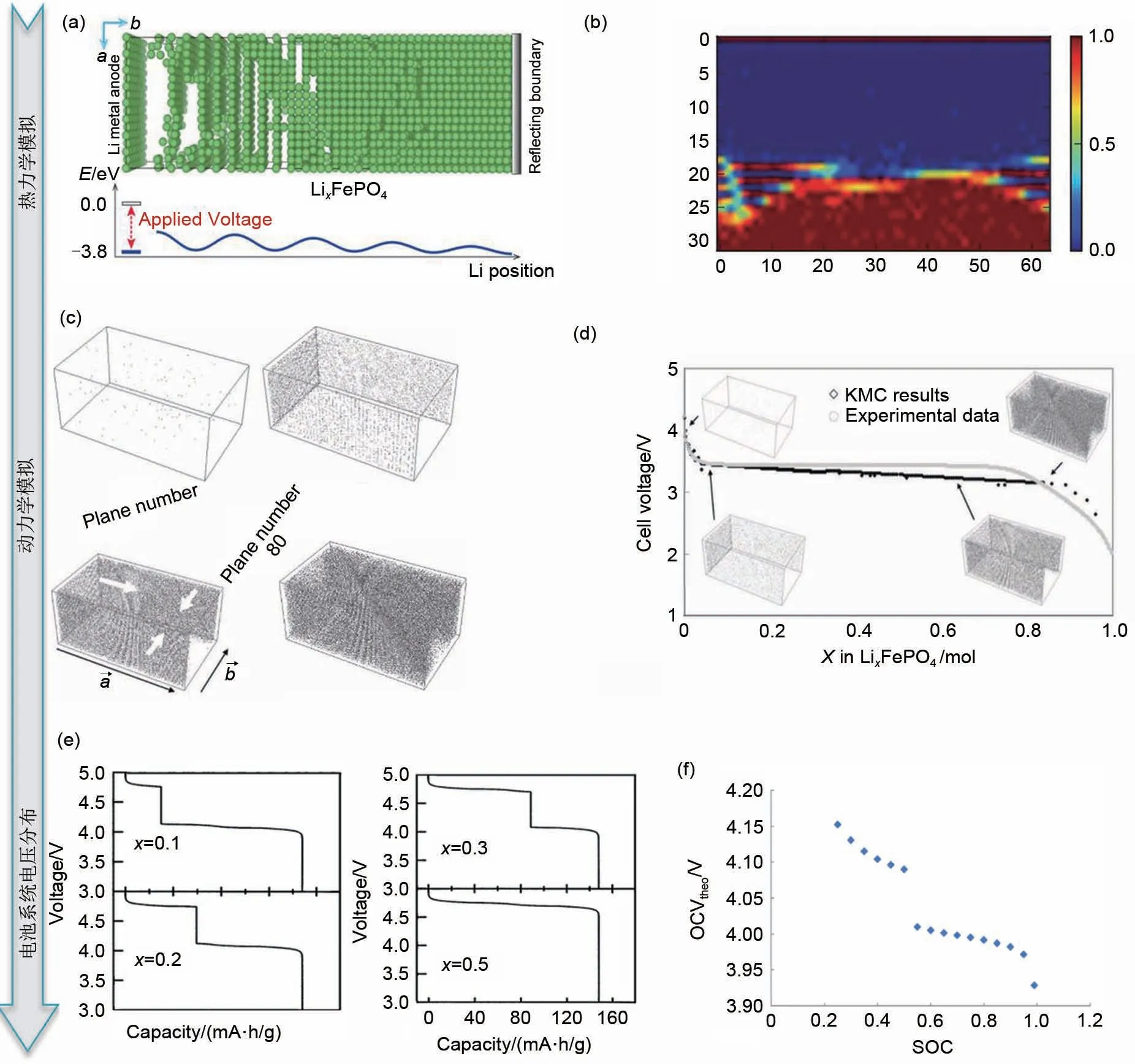
图7 MC模拟对正极材料相变与开路电压的分析：(a)MC模拟模型，上图为LixFePO4中Li的分布；下图为对应的能量图。绿色的球代表了锂离子[59]；(b)在不考虑电荷间作用能的情况下，Li离子沿着a轴的排布。如图所示，LiFePO4(LFP)和FePO4(FP)相之间形成了清晰的相边界，Li0.5FePO4相收缩到一个有限的区域[59]；(c)LixFePO4橄榄石纳米晶体在室温下恒电流放电过程的MC模拟。灰点代表活性颗粒中的锂原子，表面电流密度为0.5 A/m2。四组图分别为0 s：初始固溶体，0.0001 s：形成两个富锂相并结合在一起，0.00056 s：富锂相生长，10.81 s：贫锂相几乎完全被消耗；(d)电池电压与活性材料中Li浓度(mol)的关系[64]；(e)MC模拟计算出的Li/LiNixMn2-xO4电池电压分布，分别为x=0.1、x=0.2、x=0.3、x=0.5[65]；(f)全电池(LiMn2O4正极和碳负极)开路电位与放电期间正极材料中Ni占据率的关系[19]Fig.7 MC simulation for phase transition and open circuit voltage of positive material:(a)MC simulation model(The above figure shows the distribution of Li ions in LixFePO4,the corresponding energy diagram is shown below,the green balls represent Li ions);(b)the arrangement of Li ions along axis a without considering the interaction energy between charges.As shown in the figure,a clear phase boundary is formed between the LiFePO4 and FePO4 phases,and the Li0.5FePO4 phase shrinks to a limited region;(c)MC simulation of constant current discharge process of LixFePO4 olivine nanocrystals at room temperature.The gray dots represent lithium atoms in the active particles with a surface current density of 0.5 A·m-2.The four groups are 0 s:initial solid solution,0.0001 s:forming two Li-rich phases and combining together,0.00056 s:Li-rich phase growth,10.81 s:the Li-poor phase was almost completely consumed;(d)the relationship between the battery voltage and the concentration of Li ions in the active material;(e)the voltage distribution of Li/LiNixMn2-xO4 battery calculated by MC,x=0.1,x=0.2,x=0.3,x=0.5,respectively;(f)the relationship between the open circuit potential of a full battery(LiMn2O4 anode and carbon cathode)and the Ni occupation of the cathode during discharge

除了对正极材料相变与开路电压的模拟，MC模拟同样适用于对石墨基、硅基负极材料相特征的模拟。Moon 等[11]利用密度泛函理论(DFT)和KMC模拟，研究了锂离子插入c-Si和a-Si体系的热力学和动力学特征。DFT计算的形成能揭示了晶态硅与非晶硅在锂化过程中的相分离机制。晶态硅和非晶硅在锂化作用下的体积膨胀和相变趋势是相似的，而Li的扩散动力学在c-Si和a-Si之间则存在较大差异。在c-Si中，Li迁移势垒为0.6 eV，随着Li浓度的增加，迁移势垒迅速减小到至0.4 eV[图8(a)～(c)]。为了利用KMC模拟非晶硅中锂的扩散，首先要利用体积函数推导出非晶硅中锂迁移势垒。通过KMC 模拟发现锂在a-Si 中的扩散系数比在c-Si 中的扩散系数大一个数量级[图8(d)]。这些研究有助于在原子尺度理解锂化作用的机理，进一步阐明硅化锂的相分离过程。此外，Persson 等[66]也通过DFT、团簇扩展和MC模拟预测了LixC6相图，预测结果在高Li浓度(x＞0.5)与实验结果相吻合[图8(e)]。

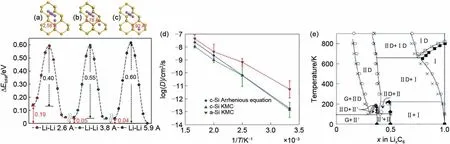
图8 Li离子排布对Li离子迁移势垒的影响[(a)～(c)][11]；(d)a-Si与c-Si中Li离子的扩散系数[11]；(e)通过MC模拟获得的LixC6的第一性原理相图。图中符号为：G为石墨，Ⅱ为Ⅱ级相，ⅡD为Ⅱ级无序相，Ⅰ为Ⅰ级相，ⅠD为Ⅰ级无序相，Ⅱ'为Ⅱ级相且Li离子组合为2×2[66]Fig.8 Effect of Li ions arrangement on the transition barrier[(a)-(c)];(d)diffusion coefficient of Li ion in a-Si and c-Si;(e)first-principles phase diagram obtained from Monte Carlo simulations.The phase regions are denoted in the following way:G(graphite),Ⅱ(stage Ⅱ),ⅡD(disordered stage Ⅱ),Ⅰ(stage Ⅰ),ⅠD(disordered stage Ⅰ),and Ⅱ′(stage Ⅱwith 2×2 Li ordering)

为区分KMC 与GCMC 模拟在电池负极材料模拟中的差异性，Arriazu 等[45]分别通过KMC 与GCMC对锂离子嵌入石墨的过程进行了分析。图9(a)所示为Dumas-Hérold锂/石墨插层化合物模型，其中蓝色代表锂离子，灰色代表石墨层，锂离子的嵌入过程呈现出多阶段(台阶)现象。离子的运动模式近似为二维运动[图9(b)]，通过KMC模拟及GCMC模拟离子嵌入脱出随时间的变化[图9(c)]，他们发现Daumas-Hérold 模型[图9(e)]中提出的结构是由于动力学限制造成的。如果系统的平衡是通过人为设置一个高交换电流密度(GCMC)的方式来实现，结构就变成了一个具有更低能量值[图9(f)]的经典Rüdorff-Hoffmann 模型[图9(d)]。因此，可以通过改变溶剂的性质来增加实验系统中的交换电流密度进而抑制DH 结构的产生。此外，使用超小的石墨薄片也有利于离子与电解质的交换，进一步抑制DH结构的产生。

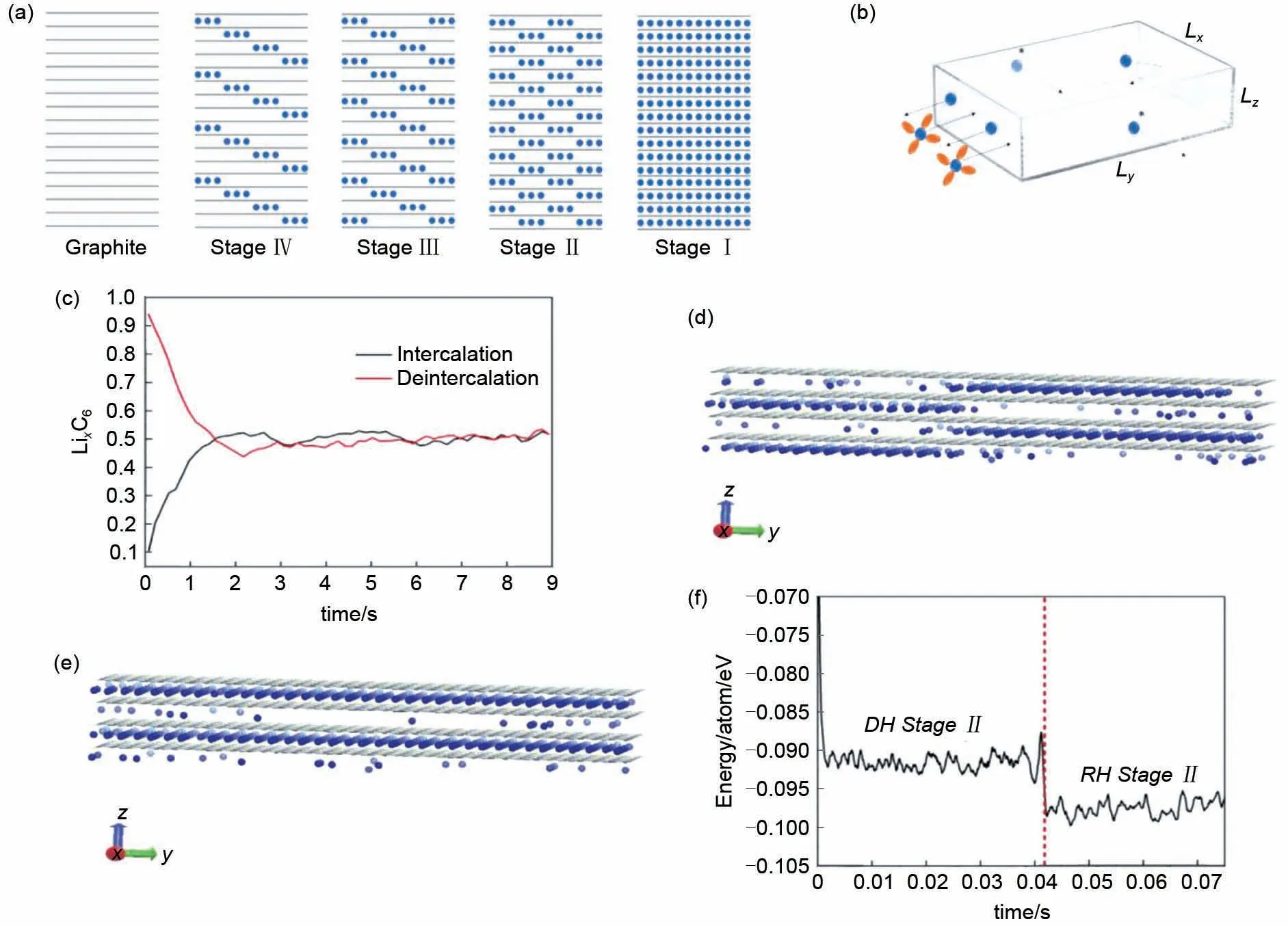
图9 MC模拟石墨负极中锂离子的排布：(a)锂/石墨插层化合物模型；(b)离子在石墨中的传导模型；(c)Li离子插入、脱出过程中的Li离子含量与时间的关系；(d)Rüdorff-Hoffmann锂/石墨插层化合物模型；(e)Dumas-Hérold锂/石墨插层化合物模型；(f)两种模型对应的能量值[45]Fig.9 Distribution of Li ions by MC simulation in graphite anode:(a)lithium/graphite intercalation compound model;(b)ionic conduction model in graphite;(c)the relationship between Li ion content and time in the process of Li ion insertion and removal;(d)Rüdorff-Hoffmann model of lithium/graphite intercalation compound;(e)dumas-Herold lithium/graphite intercalation compound model;(f)changes in energy values corresponding to the two models

3.2 离子输运特性的蒙特卡罗模拟

除了对开路电压与相变特性等的模拟，MC 也可用于对电极材料的离子扩散特性的分析。Ouyang 等[67]利用第一性原理计算得到锂离子和Cr离子在纯LiFePO4和掺Cr的LiFePO4中沿一维扩散路径迁移的迁移能垒[图10(a)]，采用MC模拟研究了势垒对锂离子二次电池正极材料LiFePO4电化学性能的影响。模拟中，Cr离子被证明不能在晶体中迁移，基于此，作者搭建了如图10(b)所示的一维离子输运模型。模拟结果显示，随着Cr 掺杂量的增加，薄膜的容量不断减小[图10(c)]，随着超胞尺寸的增大，所有掺杂量下的容量也都大大降低。这说明减小粉末正极材料的粒径可以大大提高其容量。

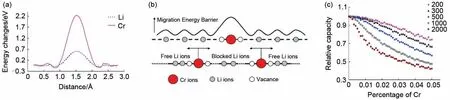
图10 (a)Cr离子与Li离子的迁移能垒示意图；(b)在每条一维通道中，锂离子被Cr离子隔开的示意图；(c)对于不同的模拟超胞尺寸，容量与掺杂量之间的依赖关系。数字200、300、500、1000和2000指的是超胞的大小[67]Fig.10 (a)schematic diagram of transition barrier between Cr ion and Li ions;(b)schematic diagram of lithium ions separated by Cr ions in each one-dimensional channel;(c)variation relation of the simulated capacity with the dopant amount and super-cell size.The numbers 200,300,500,1000 and 2000 refer to the size of the super-cell being used

对于固态电解质，其离子输运的动力学特性更加受到关注，KMC 在其中的应用更为广泛。由于典型的固态电解质存在三大特点[68]：①相邻位点之间的离子迁移容易发生；②可供迁移离子占据的位点的数量大于迁移离子的数量；③这些可用的位点连接成一个连续的扩散通路。这些特点使得格子气KMC 可以很好地适用于固态电解质材料的模拟。Morgan等[20]根据石榴石构型固态电解质的结构特征[图11(a)～(c)]，采用晶格气体MC 模拟预测了石榴石结构固态电解质LixLa3Zr2O12的相关系数变化趋势，发现当xLi=3(来自位置能量)和xLi=6(来自最近邻斥力)时，其存在特别强的相关效应[图11(d)～(e)]。

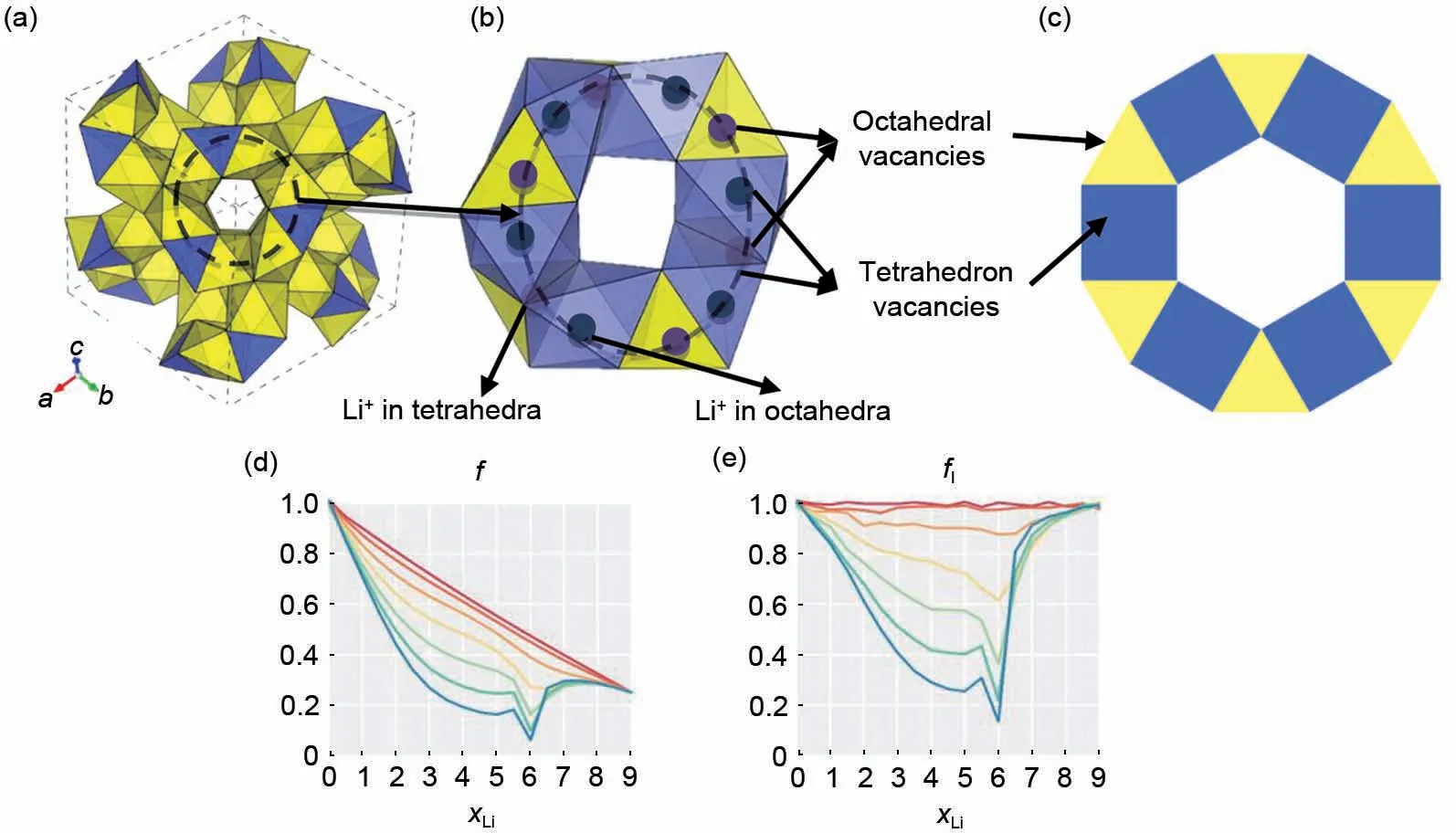
图11 石榴石框架中离子迁移扩散网络示意图与相关系数随迁移离子浓度的变化：(a)石榴石结构中由ZrO6八面体和LaO8十二面体连接的离子输运通道的三维图。迁移离子随机分布在四面体和八面体间隙中。相互连通的四面体隙和八面体间隙形成三维离子输运网络；(b)石榴石结构中环形结构示意图，其中四面体和八面体空位被部分锂离子占据。应该注意的是，并不是所有的空位都需要被锂离子占据；(c)石榴石离子输运通道的二维几何连接。一个八面体间隙与两个四面体间隙相连，一个四面体间隙与四个八面体间隙相连(四个八面体空位与四面体的每个面相连，图中仅展示两个八面体做示例)。在(a)、(b)和(c)中用蓝色表示八面体空位，用黄色表示四面体空位；(d)集体相关系数随着Li离子浓度(xLi)的变化[20]；(e)自相关系数随着Li离子浓度(xLi)的变化[20]，xLi指的是LixLa3Zr2O12中Li离子的化学计量数，取值0～9Fig.11 Schematic diagram of ion diffusion network in garnet frame and the change of correlation coefficient with Li ion concentration:(a)three-dimensional drawings of ion transport channels connected by ZrO6 octahedron and LaO8 dodecahedron in garnet structures.Migrated ions are randomly distributed in tetrahedral and octahedral spaces.The interconnected tetrahedral gap and octahedral gap form a three-dimensional ion transport network;(b)schematic diagram of partial ring structure,in which tetrahedral and octahedral vacancies are partially occupied by lithium ions.It should be noted that not all vacancies need to be occupied by lithium ions;(c)two-dimensional geometric connections of garnet ion transport channels.One octahedral gap is connected to two tetrahedral gaps,and one tetrahedral gap is connected to four octahedral gaps(four octahedral gaps are connected to each face of the tetrahedron,two of which are not drawn in the two-dimensional topology).In(a),(b)and(c),octahedral vacancies are represented by blue and tetrahedral vacancies by yellow;(d)the change of collective correlation coefficient with Li ion concentration(xLi);(e)change of autocorrelation coefficient with Li ion concentration(xLi),xLi refers to the stoichiometric number of Li ions in LixLa3Zr2O12,ranging from 0 to 9

考虑到键价和理论等静态计算方法的局限性，Chen等[8]提出将键价和理论计算的迁移能垒数据与KMC 模拟相结合的方法，得到了指定温度下的绝对电导率[图12(b)]，这显然优于仅考虑几何效应计算得到的电导率变化趋势[图12(a)]。由于迁移离子的具体排布对离子迁移能垒具有极大的影响，所以上述的近似也不够精确。为此，Ven 等[46]基于第一性原理团簇展开的方式，对KMC 模拟的势垒参数进行了计算。他们发现在无序材料中，应用团簇展开可以近似获得任何构型下的迁移势垒。这意味着在KMC 模拟中，任何时刻都能近似地保持细致平衡，并能在热力学平衡状态下计算出所需的动力学量。作者进一步给出了这一研究范式在LixCoO2中的应用。结果表明，迁移机制和激活能垒在很大程度上取决于迁移锂离子周围近邻锂离子与锂空位的排布[图12(c)]。通过模拟，作者发现在所有锂浓度下，锂在层状LixCoO2中的扩散依赖于双空位机制。此外，由于激活能垒受离子浓度影响巨大，扩散系数随锂离子浓度x的变化可以达到几个数量级。综上所述，KMC 的模拟一般依赖于其他计算方法的输入(包括模型结构，迁移能垒等)，这对计算结果精度的影响是巨大的。

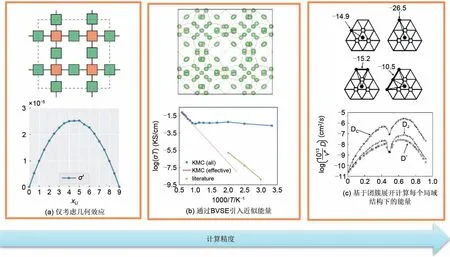
图12 几个KMC计算过程的对比：(a)LLZO的通道连接关系与仅考虑几何效应下的离子电导率示意图[20]；(b)BVSE计算得到的离子输运通道与通过KMC模拟得到的电导率与实验值的比较。实心蓝色曲线和填充圆表示KMC所模拟的电导率。实红线表示有效计算的电导率(来自高温KMC模拟)，虚线表示对较低温度下离子电导率的推断。三角形绿色曲线表示实验电导率数据[8]；(c)几种典型的离子排布状态与基于局域结构团簇展开的KMC计算得到的离子扩散系数[46]Fig.12 Comparison of several KMC calculation processes:(a)schematic diagram of channel connection and ionic conductivity of LLZO only considering geometric effects;(b)ionic transport channel calculated by BVSE and the comparison of ion conductivity calculated by KMC with experimental observation.Solid blue curves and filled circles represent the ion conductivity simulated by KMC.The solid red line represents the ion conductivity effectively calculated(from the KMC simulation at high temperatures)and the dashed line represents the inferred ionic conductivity at lower temperatures.The triangular green curve represents the experimental observation conductivity;(c)several typical ion distribution states and the ion diffusion coefficient calculated by KMC based on cluster expansion[46]

考虑到KMC 模拟可以有效地预测和分析晶体材料离子电导率，Grieshammer等[57]开发了一款名为MOCASSIN 的固态离子导体MC 计算软件，利用该软件对富镧橄榄石中的氧间隙迁移以及掺杂全水合锆酸钡中的质子传导进行了模拟研究。模拟结果揭示了缺陷相互作用对离子电导率的影响。这些效应的组合可能会导致固态离子材料中意想不到的离子输运行为，特别是在具有较多可移动离子的模拟体系中。除此之外，Hoffmann 等[58]也开发了一款名为Kmos的软件，在软件描述的系统中，所有的反应空间都可以抽象为一系列离散的空间格点(即为前文的格子气模型)。Kmos 通过代码生成新的可用事件来不断演化，以实现较高的模拟效率。

3.3 晶体生长及电解质界面膜(SEI 膜)生成的蒙特卡罗模拟

除上述对离子导体材料的模拟之外，MC 模拟在晶体生长以及SEI膜层生长等领域也有着重要的应用[69]。基于晶体生长理论的计算模拟是深入研究晶体生长机理，进一步指导晶体生长实验的一项重要技术。MC 在模拟晶体生长的过程中分别考虑了原子的沉积、表面扩散、吸附等过程。在KMC 模拟中，晶体的生长过程可被视为一个随机过程，使用某些特定的生长模型来描述其中随机事件的发生概率。通常具体模拟步骤如下：①建立微观模型；②对模型进行描述；③模型发生演变；④比较演变前后的结果确定演变概率，这与第二部分的相关总结类似。图13(a)～(g)展示了简立方晶格模型的表面在不同配位下的晶体生长过程，可以看出这几种配位对晶体长大的速度与方向均会产生极大的影响[70]。Barai 等[71]基于简化的二维格子气模型通过KMC 模拟建立了一个多尺度计算模型，用以捕捉晶体初生离子的形核和生长以及它们聚集成二次过渡金属氢氧化物前驱体离子。结果显示随着溶液pH的增加和氨浓度的降低，二次颗粒的尺寸减小。结合模拟给出的相图[图13(h)]，相关研究可以为实验合成提供有效指导。Chen等[72]采用KMC模拟研究了4H和6H型SiC的竞争生长过程。该模型以硅和碳原子为基本迁移离子，构建了格子气KMC 模型。该模拟不仅考虑了同种原子之间的相互作用能(Si-Si)，还考虑了不同类型原子之间的相互作用能(Si-C)。基于此模型，作者进一步研究了生长条件对4H-SiC 和6H-SiC 竞争生长的影响。结果表明，在生长过程中较高的温度和高比例的Si 源会促进6H相的生长。同时，随着温度和Si/C比的升高，晶体表面原子聚集生长的现象越来越明显[图13(i)～(j)]。KMC 模拟SEI 的生成过程一般分为如下几个过程：吸附、解吸、表面扩散以及钝化(非活性)材料的形成[图13(k)]。基于此流程，Hao 等[73]利用KMC研究了充电期间石墨电极上SEI的生长过程。结果显示，锂离子的嵌入速率和充电时间均受锂还原速率和通过SEI的锂传输速率的控制。在较低的温度下，Li的还原速率较高，但SEI的电阻也较高，所以会限制扩散过程。另一方面，在较高温度下，较低的Li还原速率会导致总充电时间增加[图13(l)]。

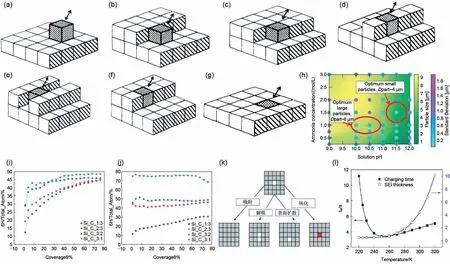
图13 (a)～(g)为简单立方晶格表面不同配位下的晶体生长过程[70]；(h)晶体尺寸与溶液pH值与氨含量依赖关系的相图。图中显示了在粒径分布为高斯分布的情况下，溶液的平均粒径及其对应的一阶标准差。这里显示的所有数据都是从计算模型中获取的。绿色区域表示次级颗粒较小，黄色区域表示次级颗粒较大。浅蓝点的二次粒径分布标准差较小，紫色点的二次粒径分布标准差较大。在pH值和氨含量方面，沉积较大(Dpart约8 μm)和较小(Dpart约4 μm)的二次活性颗粒的最佳操作条件也在图中突出显示(用红色圆圈表示)[71]；(i)T=1100 K下的不同Si/C比条件下，两种晶体在沉积速率F=0.1 ML/s下，6H-SiC在生长中的比例[72]；(j)T=1400 K下的不同Si/C比条件下，两种晶体在沉积速率F=0.1 ML/s下，6H-SiC在生长中的比例[72]；(k)SEI膜的生成过程，一般分为吸附、解吸、表面扩散和钝化等步骤；(l)SEI膜厚度、充电速度与温度的依赖关系[73]Fig.13 (a)-(g)the crystal growth process on the surface of a simple cubic lattice under different coordination;(h)Phase diagram of the dependence of crystal size on solution pH and ammonia content.The figure shows the mean particle size of the solution and its corresponding first standard deviation in the case of gaussian particle size distribution.All the data is taken from the computational model.Green areas indicate smaller secondary particles and yellow areas indicate larger secondary particles.The standard deviation of the secondary particle size distribution of the light blue dot is smaller,and the purple dot is larger.Optimum operating conditions,in terms of pH and ammonia content,for precipitating relatively larger(Dpart～8 μm)and smaller(Dpart～4 μm)sized secondary active particles,have also been highlighted within the figure(by red circles);(i)under different Si/C ratio conditions at 1100 K,the ratio of 6H-SiC in the growth of the two crystals at the deposition rate F=0.1 ML/s;(j)under different Si/C ratio conditions at 1400 K,the ratio of 6H-SiC in the growth of the two crystals at the deposition rate F=0.1 ML/s;(k)the generation process of SEI film is generally divided into adsorption,desorption,surface diffusion and passivation,etc.(l)the dependence of SEI film thickness,charging speed and temperature

目前对晶体生长的MC 模拟仍存在许多问题，比如Maazi 等[53]模拟晶体生长时，在随机矩阵位点上需要重复数百万次晶粒生长过程。这对于较大的晶格系统来说计算时间会很长。为了提高晶粒生长模拟的计算速度，研究人员对经典MC模型进行了两种修正：①所有阵点都以相同的概率进行随机重定向，即每个蒙特卡罗步都不重复；②位置能量除以一个参数，该参数表示离子存在时，作用在晶界上的有效作用。这些举措极大地加速了大颗粒的生长，减弱了邻近小颗粒的生长，有效地提高MC模拟的速度。

4 结论与展望

本文总结了MC模拟的发展历史，归纳出了一套适用于多数MC 模拟的范式，包括以下几个部分：模拟目标的确定、模拟参数与模拟模型的设定、结构演化方式的选择、转换过程中判据的提取(如体系能量)、新结构接受概率的计算、样本数据的获得等。根据此范式，列出了本团队前期开发的一套典型MC模拟代码供读者参考使用，并给出了一个典型的计算案例：预测石榴石结构固态电解质的有效载流子浓度、迁移离子分布与迁移离子浓度的依赖关系，模拟结果与实验规律基本一致。除此之外，本文就其在正负极材料、电解质以及相关界面中的典型热力学与动力学计算案例进行了剖析，包括求解离子导体中的离子扩散问题、模拟迁移离子的分布特征与相关界面层的生长过程等。这些计算不仅涵盖了实验现象的微观机理解释，也包含了实验结果的预测进而提供具体的实验方案指导。在与实验结合方面，MC 模拟可以基于某些实验数据(如迁移离子的分布)搭建初始模型，提出针对具体研究体系的改进策略。如Huang等[74]基于实验观测，提出了层状金属氧化物中过渡金属在八面体位点与四面体位点的迁移会改变迁移离子的输运特性。鉴于每种模拟方法本身的局限性[75]，亦可以采用多方法联用的方式，扩展MC模拟的输出，比如文中提到的KMC 与渗流的结合以获得有效载流子浓度。为了促进MC模拟在离子导体计算中的发展，本文总结了以下几个MC方法的发展方向，包括：①在MC 模拟中如何快速精确地获取所有可能发生的事件以及对应的转变概率。在材料计算领域，这些事件及其描述主要是通过实验测试以及第一性原理计算的方式获得，比如通过密度泛函理论(DFT)计算迁移能垒，通过分子动力学预判离子的迁移模式等。然而这些参数的计算需要解决微观演变中所涉及到的各种近似，比如基于第一性原理模拟的团簇展开就是对能量计算的一种简化近似。除此之外，体系转换速率因子也直接决定了模拟体系的演变速度，该参数一般需要近似为某一个常数，但对于一些复杂体系(比如存在多种迁移模式的晶态离子导体)，转换因子(如离子的迁移尝试频率等)是极为复杂的，虽然通过声子谱等手段可以进行较为精细的计算，但对于较大体系或者较长时间的模拟，相关的计算成本是巨大的。②晶格气体MC模拟过程中仅考虑了当前对模拟体系有利的转移路径，这将导致模拟会很快进入某一亚稳态。当前常用的Metropolis 算法虽然能够一定程度上改善此问题，但对于存在多个亚稳态的模拟体系，以上算法还是很难精确地寻找到系统的演化轨迹，并且其计算成本也极为高昂。③MC 模拟过程中，模拟事件之间存在先后顺序，这不仅制约了其计算效率也影响了其模拟准确性。比如在极短时间内离子的迁移存在一定的先后顺序，如何确定迁移的先后顺序会直接影响离子迁移的成功率。④MC 模拟始终在“自己的”时间域内进行，与真实时间存在差异。虽然可以通过数学手段对MC 时间(也叫做蒙特卡罗步)与真实时间进行转换，但这种转换仅为统计上的一种近似，依赖于众多初始输入参数(如尝试频率等)。