基于扩展卡尔曼滤波的环路跟踪算法仿真分析*
阎 磊,曲全福,白 涛,舒东亮,周 超
(1.天津职业大学电子信息工程学院,天津 300410;2.海军驻大连四二六厂军事代表室,辽宁 大连 116005;3.解放军92956 部队,辽宁 大连 116041;4.天津航海仪器研究所,天津 300131)
0 引言
卫星导航系统可在全球范围内提供全天候的高精确位置、速度、时间信息,在军用、民用领域应用广泛。卫星接收机主要由射频前端单元、信号捕获单元、信号跟踪单元与导航解算单元4 个关键模块组成,其中,信号跟踪模块包括码跟踪和载波跟踪两个方面,码跟踪实现对卫星接收信号的码相位的精确跟踪,用于伪距信息的计算;载波跟踪实现对卫星接收信号载波的跟踪,获得测速所需的伪距率信息。经过码跟踪和载波跟踪,实现卫星接收信号的码解调和载波解调,进而获得导航电文信息,用于导航定位解算。信号跟踪单元中得到的导航电文的质量、伪距和伪距率观测信息的精度对卫星接收机定位、测速精度具有直接影响。
在超高动态环境中,卫星接收机接收的信号载波将存在比较大多普勒频率与多普勒频率变化率,以往一般根据载体动态性和接收信号环路噪声的权衡来选择合适的跟踪环路带宽。文献[5]提出的采用锁频环辅助锁相环的载波跟踪算法中,由于锁频环的动态适应性较好,在高动态下须切换至锁频环,从而导致观测值精度的大大降低。文献[6-7]提出用其他传感器信息对接收机跟踪环路进行辅助,从而降低环路所需承受的动态性,但这将增加额外的传感器,且观测值精度也将受到辅助传感器自身性能的影响。文献[8-9]提出了基于标准卡尔曼滤波的环路跟踪算法,但其码相位与载波相位精度将受限于采用鉴别器的线性度。文献[10]提出了基于扩展卡尔曼滤波的接收机环路跟踪技术。本文在学者们研究的基础上,对基于扩展卡尔曼滤波的接收机环路跟踪算法进行了全面的仿真分析,研究结论可为工程应用提供参考。
1 信号模型
图1 给出了基于标准卡尔曼滤波的接收机载波跟踪环路的原理图。

图1 基于标准卡尔曼滤波的载波跟踪环路
首先采用本地数控振荡器(NCO)产生的载波信号与接收机数字中频(SIF)信号相乘,实现信号载波的剥离,载波剥离后,得到同向()信号与正交()信号。而后,信号分量与信号分量再与本地产生的即时()码进行相关计算,得到剥离伪随机码和载波的信号与信号,如下所示:

对剥离载波和伪随机码后得到的信号相干值进行积分累加,分别得到相干积分I、Q,如下所示:

式中,N为相干积分时间之间进入积分器数据的数目。将式(1)代入式(3),式(2)代入式(4)可得:

2 基于标准卡尔曼滤波跟踪算法
在基于标准卡尔曼滤波的接收机跟踪算法中,经过载波环路鉴别器得到载波相位误差θ和频率误差f,将其选为卡尔曼滤波器观测量。而后利用卡尔曼滤波结果计算载波NCO 的控制变量,进而实现稳定跟踪载波环路。
采用载波跟踪的相位误差、频率误差以及频率变化率误差作为卡尔曼滤波状态量,为
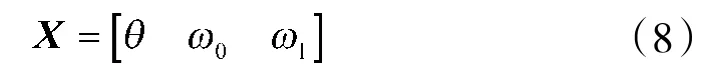
式中,代表本地载波存在的相位误差,代表本地载波存在的多普勒频率误差,代表本地载波存在的多普勒频率变化率的误差。
对本地载波进行线性化,得到离散化的状态方程,为

3 基于扩展卡尔曼滤波环路跟踪算法
基于扩展卡尔曼滤波环路跟踪算法的状态方程与基于标准卡尔曼滤波环路跟踪算法一致,差别在于观测方程。基于扩展卡尔曼滤波环路跟踪算法不同以鉴别器输出的相位误差和频率误差为观测量,二是用、支路的累加值I和Q作为观测量,其原理框图如图2 所示。

图2 基于扩展卡尔曼滤波跟踪环路
即它的观测方程为

其中,

根据EKF 原理,在当前状态估计值处,对观测向量一阶求导,从而得到观测矩阵H,为
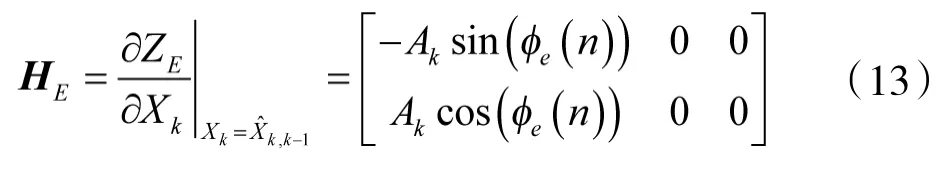
从上可知,整个接收机载波环路滤波过程可分为状态预测、状态更新两部分,步骤如下:
1)预测
对状态进行一步预测,为:

对状态均方误差进行一步预测,为:

2)更新
对滤波增益进行更新,为:

对状态进行估计的方程为:

对状态均方误差进行更新为:

4 仿真结果分析
4.1 动态性分析
采用国防科大的卫星信号模拟器产生GPS 射频信号,通过中频信号采样器实现GPS 数字中频信号的采集。中频信号采样器的采样率是62 MHz,得到的数字信号的载波频率是8.58 MHz。设计的运动场景中,载体初始向北运动,速度为10 m/s,加速度为10 g。
图3 给出了基于卡尔曼滤波和扩展卡尔曼滤波环路跟踪算法的路累加值图。理论上,GPS 接收机路信号累加值是方波形状,即数值横轴两侧,远离0 值,距离横轴距离越远,电文越不容易判错。从图3 中可知,基于扩展卡尔曼滤波环路跟踪算法的路累加值的绝对值大于基于卡尔曼滤波的环路跟踪算法,也就是说基于扩展卡尔曼滤波的环路跟踪算法的动态性优于基于卡尔曼滤波的环路跟踪算法。

图3 基于KF和EKF 环路跟踪算法动态性分析
4.2 跟踪灵敏度分析
采用数据仿真生成GPS 中频信号,据此评估对不同接收机载波跟踪算法的灵敏度。生成信号的采样率为62 MHz,对应的数字信号载波频率是8.58 MHz,所有的数据位都采用正1 表示。
图4 给出了载体静止时,基于卡尔曼滤波的载波环路跟踪算法的灵敏度估计。从图4 可知,在接收信号信噪比是-36 dB 时,在基于卡尔曼的载波环路跟踪算法中,路累加值一直在横轴上部分,没有出现在横轴下部分,即数据位一直判为1,没有出现错判。当接收机信噪比为-37 dB 时,接收机载波环路中级,路累加值不再维持在横轴上部分,而是出现在横轴下部分,即存在负值。由此认为,基于卡尔曼的环路跟踪算法跟踪灵敏度的信噪比为-36 dB。
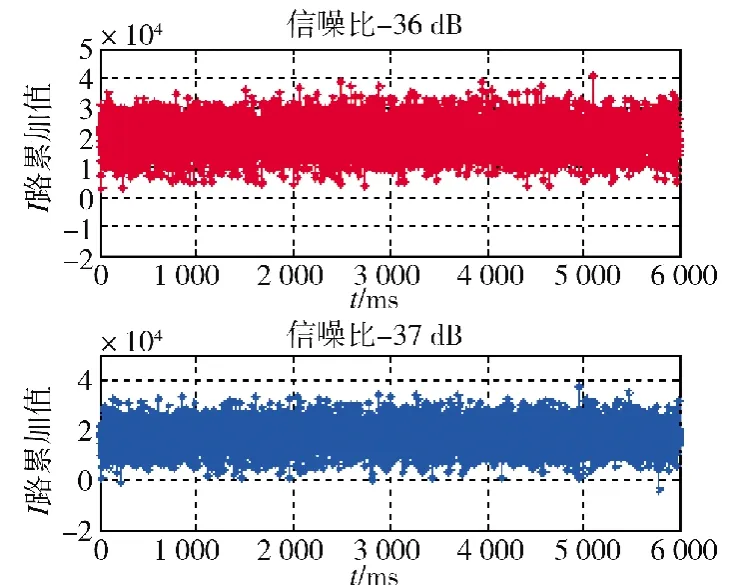
图4 基于卡尔曼滤波跟踪算法跟踪灵敏度
图5 给出了基于扩展卡尔曼滤波的接收机载波跟踪算法跟踪的灵敏度。从图5 中可知,当接收信号信噪比为-37 dB 时,得到的路累加值一直在横轴上部分,没有出现负值;然而,当接收信噪比为-38 dB 时,得到的路累加值有部分在横轴下部分,存在负值,也就是数据位将存在误判的可能,由此认为基于扩展卡尔曼滤波的载波跟踪算法灵敏度的信噪比为-37 dB。
对比图4和图5 可知,基于扩展卡尔曼滤波载波跟踪算法,相比基于标准卡尔曼滤波载波跟踪算法的跟踪灵敏度提升1 dB。
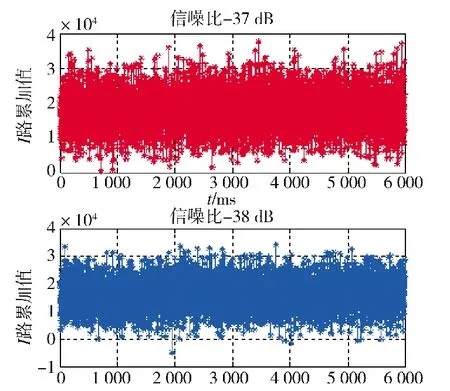
图5 基于卡尔曼滤波跟踪算法跟踪灵敏度
5 结论
本文首先推导了基于标准卡尔曼滤波的接收机载波跟踪算法的基本原理,在此基础上对比分析了基于扩展卡尔曼滤波的原理,给出了原理框图和理论推导。而后分别基于采集的国防科大的卫星信号模拟器的数据以及数据仿真产生的中频信号,对比分析了基于扩展卡尔曼滤波环路跟踪算法和基于标准卡尔曼滤波环路跟踪算法的性能。仿真结果表明,基于扩展卡尔曼滤波的环路跟踪算法,相比基于标准卡尔曼滤波的环路跟踪算法具有更好的动态适应性,且能够改善跟踪灵敏度。

