特殊构型热电腿增强同位素温差电池输出性能

边明鑫， 许志恒,2， 汤晓斌,2， 何宇航， 王辰

(1.南京航空航天大学 材料科学与技术学院，江苏 南京 211106； 2.空间核技术应用与辐射防护工业和信息化部重点实验室，江苏 南京 211106)

随着人类对深空探索的不断增加以及探测任务的多元化，多用途、高能耗的电子设备应用在航天器内，对航天器内的电源供应提出了更高的要求[1-2]。长寿命、高稳定性、高能量密度的同位素温差电池几乎成为深空探测的唯一可用电源[3]。同位素温差电池是将同位素衰变产生的热能直接转换为电能的装置，通常由同位素热源、热电器件和散热器3部分组成[4-5]。其中，热电器件基于Seebeck效应将其两端的温差转换为电能。热电器件由多组P/N型热电腿经电极连接而成，因此热电腿的输出性能直接决定同位素温差电池的输出性能。热电腿的能量转换效率不仅与其内部材料的热电性质有关，还受其两端温差的影响[6-7]。在同位素温差电池的设计中，不仅要提升热电材料的ZT值，还要增加热电腿两端的温差。

热电腿两端的温差不仅与内部材料的热导率有关，还受内部热流的流动方式、几何形状及外界环境等因素的影响。学者们通过优化热电腿的几何形状提升其输出性能，Sahin等[8]通过理论计算证明了热电腿的形状因子可以改善其输出性能；Zebin等[9]制备了一种可伸缩的螺旋结构的热电器件，能够产生可调的温差和优异的电学输出；Yohann等[10]模拟了3种几何形状的热电腿，结果显示层状结构的热电腿表现出最佳的输出性能。然而，基于优化热电腿的几何形状及热量流动方式来增加温差和输出性能的研究较少。

本文基于增加热电腿的侧面积从而增加侧面上的散热提出了螺旋构型和轮辐构型2种特殊几何构型的热电腿的设计方法，并通过傅里叶热传导定律分析了特殊构型对热电腿性能提升的原理，使用有限元分析的方法对2种热电腿进行了几何参数优化及器件性能分析，所得的热电腿输出性能随几何参数的变化规律可以为应用在太空、极地、深海等不同场景下的小型同位素温差电池的几何设计提供参考与指导。

1 热电腿的设计与研究方法

1.1 热电腿几何设计

本文基于增加热电腿侧面面积以提升散热效果，提出了2种特殊构型热电腿的几何设计方法。其中，螺旋构型热电腿基于在热电腿的朝向和热流流向之间产生夹角从而增加侧面积；轮辐构型热电腿基于改变热电腿的截面形状、增加截面周长来增加侧面积[11]。2种特殊构型热电腿的设计方法如图1所示。

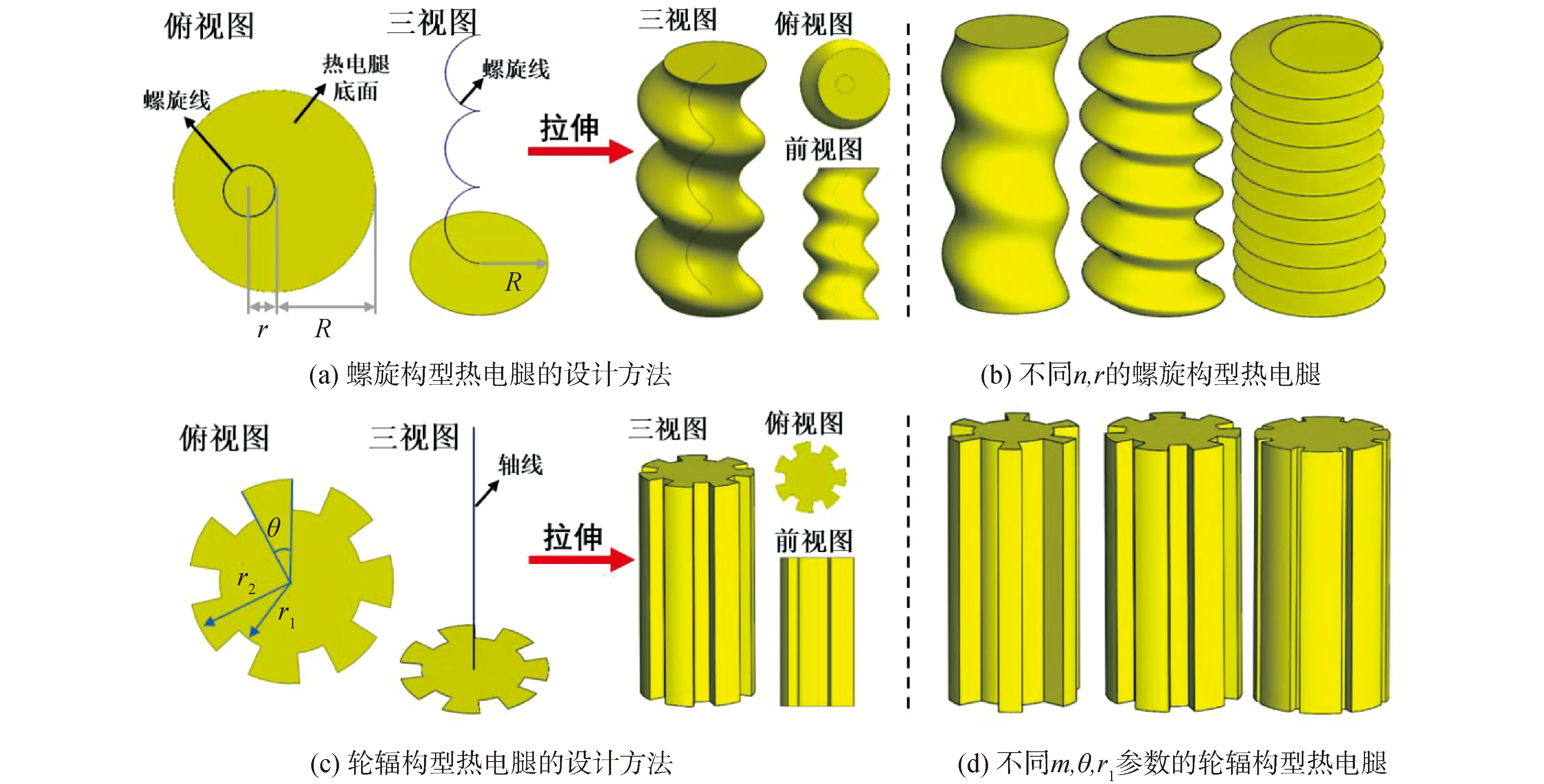
图1 2种特殊构型热电腿的设计方法Fig.1 Design method of two thermoelectric legs with special geometrical shapes

螺旋构型热电腿由底面沿螺旋线拉伸而成，如图1(a)所示，其中底面半径和螺旋半径分别设为R和r，螺旋线的圈数设为n。热电腿的底面沿螺旋线拉伸过程中平行于水平面，热电腿的体积和质量由底面面积和高度决定，螺旋半径r和螺旋圈数n不影响热电腿的体积。图1(b)展示了具有不同n和r的螺旋构型热电腿。轮辐构型热电腿由底面沿轴线拉伸而成，如图1(c)所示，其中轴线与底面垂直。在底面上设置多个轮辐结构来增加底面周长，从而增加侧面面积。通过调整内外半径r1，r2，轮辐结构的数量m和张角θ来调整底面积和周长。图1(d)展示了具有不同几何参数的轮辐构型热电腿。

对螺旋构型热电腿来说，侧面面积随着n、r增加而增加，与此同时，载流子通路也随着n、r的增加而延长，这导致热电腿的内阻随n、r增加而增加。对轮辐构型热电腿来说，其底面周长和底面面积由内外半径r1、r2和轮辐数量m、张角θ共同决定，由于轮辐构型热电腿由底面沿轴线垂直拉伸而成，因此其内阻由底面面积和高度的决定，而不受底面周长的影响。

1.2 热电腿的传热分析

热电器件将热能转换为电能的过程中，热量沿着轴向从热电腿的热端流向冷端，并从侧面和顶面散发到外界环境中，这个过程遵从一维傅里叶热传导定律为[12]：

(1)

式中：t表示热电腿微元内的平均温度；x表示热流流动的距离；Φ为微元内的产热，由于热电腿内只有散热过程，因此为负值；λ为热电腿内的热电材料的热传输系数。不同几何构型热电腿内的热传导如图2所示。

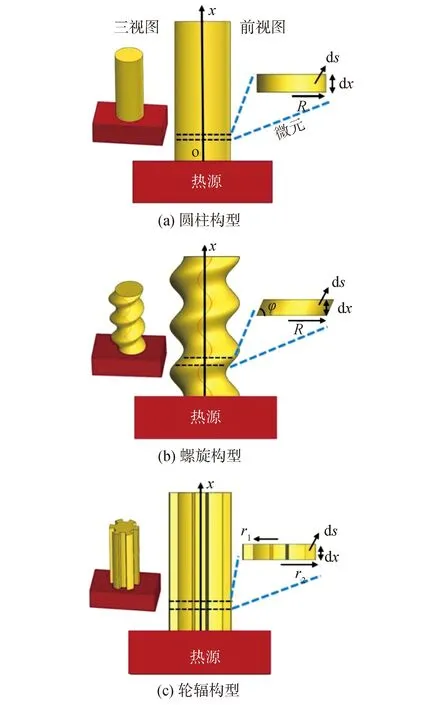
图2 不同几何构型热电腿的热传导示意Fig.2 Schematic diagram of heat transfer of thermoelectric legs with different geometrical shapes

对热电腿来说，微元内的产热(实际为散热)为：

(2)

式中：dV表示微元的体积；Φs为微元侧面上的散热。热量从热电腿的侧面以辐射散热Φrad和对流散热Φcon2种方式散发到环境中，可以表示为：

Φs=Φrad+Φcon

(3)

(4)

Φcon=h(t-t∞)ds

(5)

式中：ε为热电材料的发射率；σ为斯忒藩-玻尔兹曼常数，其值为5.67×10-8W/(m2·K4)；h为热电材料的对流传热系数；t∞表示环境温度。

热电腿的冷热端温度可以由边界条件及求解热传导方程得到。对热端来说，当热源表面温度固定时，可以表示为：

t=t0|x=0

(6)

式中t0为热源表面温度。当热源表面的热功率固定时，可以表示为：

(7)

式中q0为热源表面的单位热功率，W/m2。

对冷端来说，热电腿的顶面以辐射和对流散热的方式向环境中散发热量：

(8)

式中H为热电腿的高度。

传统圆柱构型热电腿的侧面上的散热Φs-cylinder可以表示为：

(9)

而本工作提出的2种特殊构型热电腿的侧面上的散热可以表示为[11]：

(10)

(11)

式中：Φs-spiral表示螺旋构型热电腿侧面上的散热；Φs-spoke表示轮辐构型热电腿侧面上的散热。

根据上述分析可知，相比于传统圆柱构型热电腿，螺旋构型和轮辐构型热电腿由于具有更大的侧面积，从而向环境散发更多的热量，进而降低了热电腿的冷端温度并增加了冷热端的温差。

热电腿基于Seebeck效应将其两端的温差转换为电压，开路电压Voc和输出功率P及功率密度Pd的表达式为[13-14]：

Voc=S·ΔT

(12)

(13)

(14)

式中：S为Seebeck系数；ΔT为热电腿两端的温差；Rin、RL分别表示热电腿的内阻和外接负载的电阻；V表示热电腿所占的空间体积。当Rin=RL时，输出功率达到最大，可以表示为：

(15)

传统圆柱构型和轮辐构型热电腿的内阻为：

(16)

式中：ρ为热电材料的电阻率；H、A分别表示为热电腿的高度和底面积。由于螺旋构型热电腿在热流流向和热电腿朝向之间产生了夹角，这延长了载流子的路径，其内阻公式可以表示为[11]：

(17)

式中φ表示螺旋构型热电腿的倾角。当底面积和高度相同时，轮辐构型热电腿具有与圆柱构型热电腿相同的内阻；而螺旋构型热电腿的内阻更大。

1.3 热源与参数设置

在现阶段的同位素温差电池的设计中，通常使用NASA设计的通用热源(general purpose heat source，GPHS)模块作为热源。GPHS热源的设计如图3(a)所示，一个GPHS热源模块包含4个热功率为62.5 W的238PuO2芯块，4个热源芯块由多层碳纤维材料固定在封装外壳内[15-16]。GPHS热源的外形尺寸为9.72 cm×9.32 cm×5.31 cm，热功率250 W[17]，经计算其表面热功率为6.51 mW/mm2。将GPHS热源的表面热功率作为恒定功率热源条件进行后续研究。使用有限元分析软件COMSOL模拟不同几何参数的特殊构型热电腿在恒定热源温度和恒定热源功率条件下的输出性能，分析几何优化对输出性能的影响规律。在有限元模拟计算中，选用六面体网格对热源、热电腿和电极进行网格划分，六面体的尺寸为0.002 4～0.024 mm，在对热源的划分中，由于几何形状规则且内部热流流动方式简单，六面体尺寸相对偏大；而对热电腿和电极的划分中，由于尺寸小、形状复杂、热量流动复杂，因此六面体尺寸相对偏小。在使用COMSOL软件对热电器件的相关研究中发现，网格尺寸的差异对模拟结果影响可以忽略不计，为保证模拟结果的准确性，本文选取的尺寸为COMSOL 5.4版本中最精细的网格尺寸。

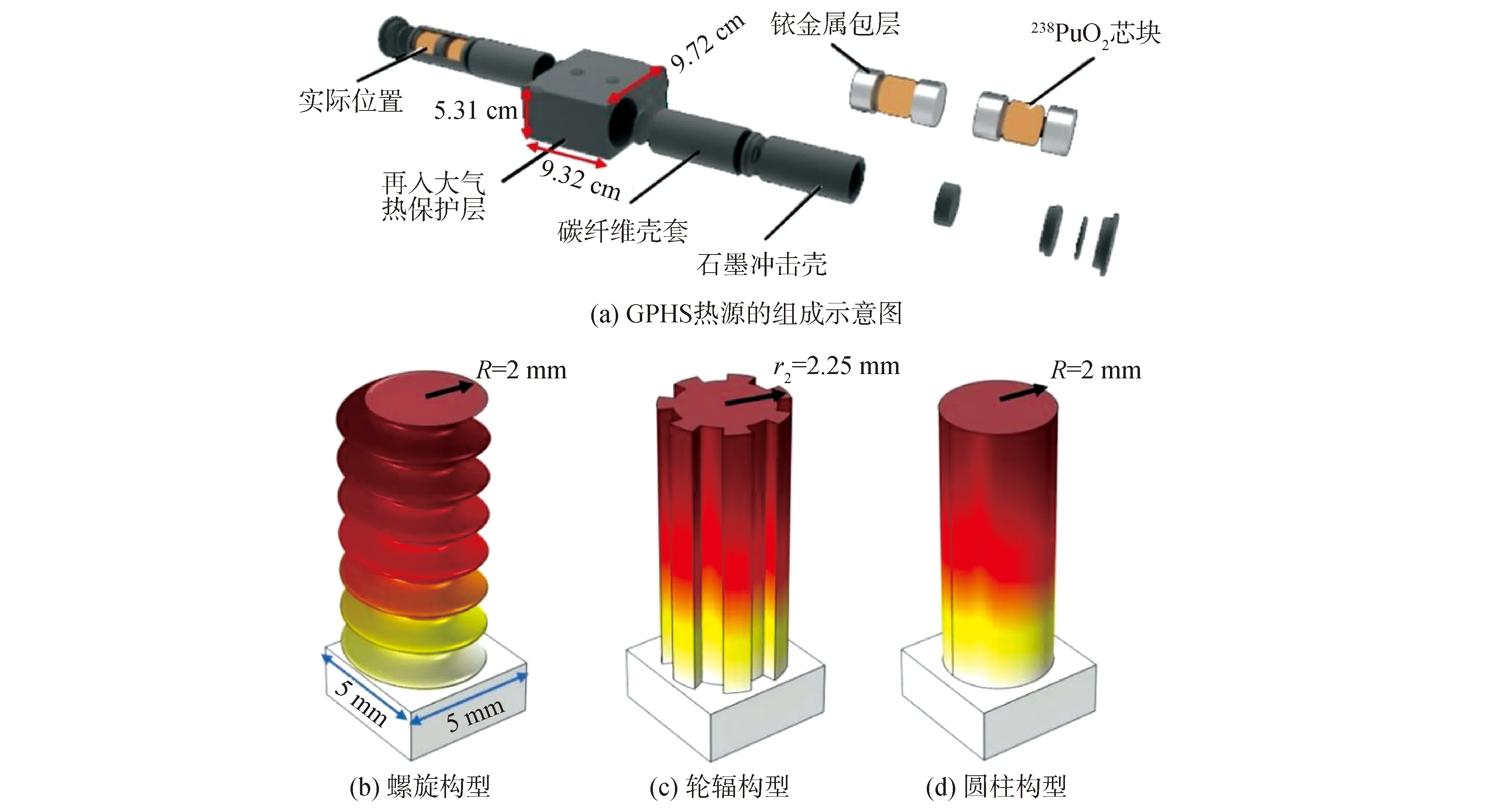
图3 GPHS热源及有限元分析中不同几何构型热电腿的示意Fig.3 Schematic diagram of GPHS heat source and thermoelectric legs with different geometrical shapes in COMSOL

在热电腿的几何参数设计中，选取与螺旋构型、轮辐构型热电腿具有相同底面积和高度(相同质量)的圆柱构型热电腿作为对照组。圆柱构型和螺旋构型热电腿的底面设置为半径R=2 mm的圆形；轮辐构型热电腿的外半径设置为r2=2.25 mm，调整内半径r1和轮辐的数量m和张角θ使其具有与圆柱构型热电腿相同的底面积。特殊构型热电腿的几何变量如表1所示。为了更加符合真实情况，模拟程序中热电腿放置在边长为5 mm的热源上，恒定热源温度设置为500 K，3种构型热电腿的示意图如图3(b)～(d)所示。选取商用Bi2Te3(P/N型)的热电参数(Seebeck系数、电导率、热导率)作为模拟工作中热电腿内材料的热电参数[18]。

2 输出性能讨论与分析

2.1 圆柱构型热电腿

本文传统圆柱构型热电腿的底面半径R为2 mm，在恒定功率的热源条件下分析其输出性能随高度的变化规律，确定最佳高度。圆柱构型热电腿的散热性能和电学输出性能随高度的变化如图4。

表1 特殊构型热电腿的几何参数

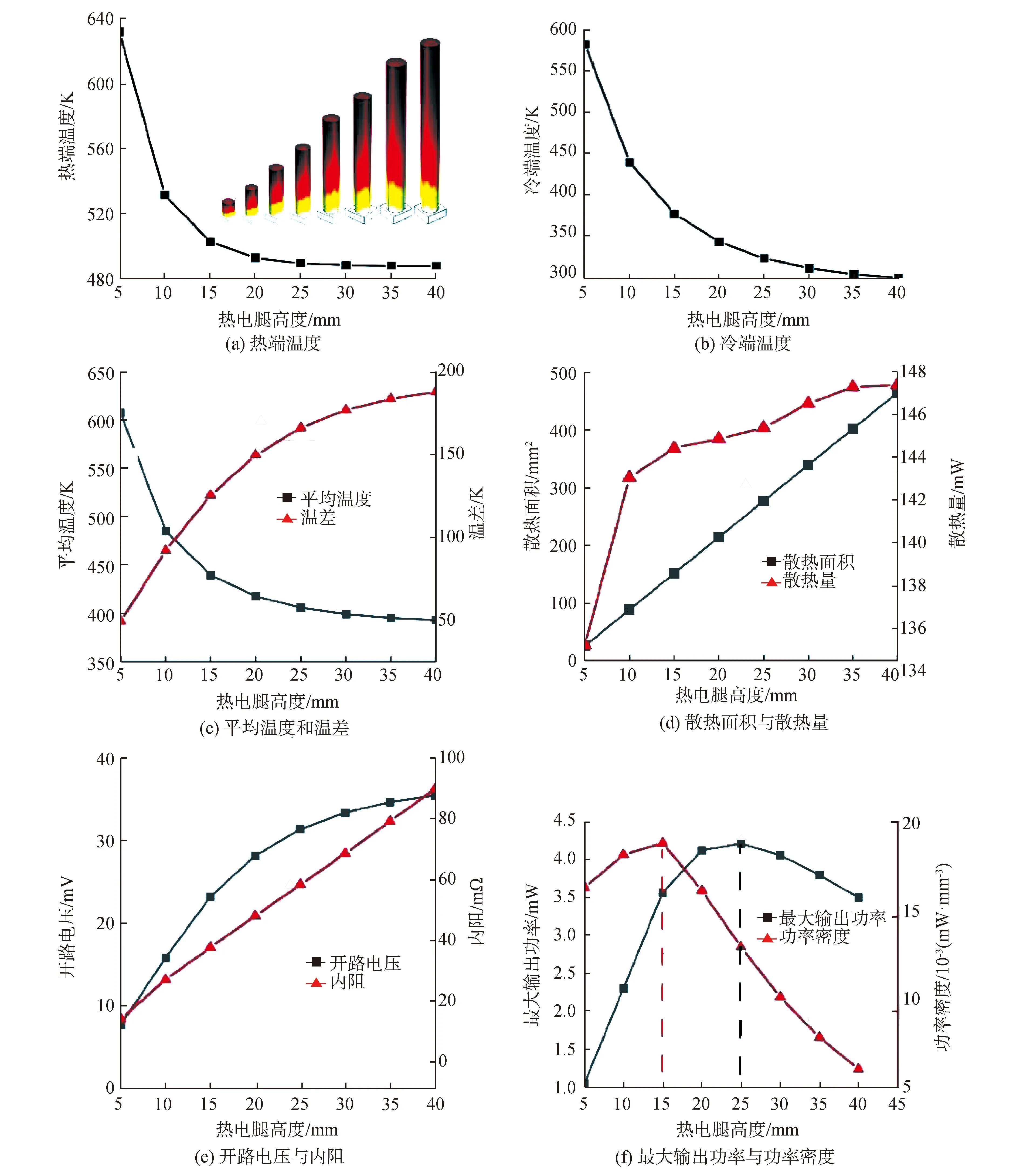
图4 圆柱构型热电腿的散热性能与输出性能随高度的变化规律Fig.4 Variation of heat dissipation and output performance with height of the cylinder-shaped thermoelectric leg

圆柱构型热电腿的散热效果如图4(a)～(d)所示，其冷、热端的温度和平均温度都随着高度的增加逐渐降低随后趋于饱和，这是由于随着高度的增加，热电腿拥有更大的散热面积(侧面积与顶面积之和)用于散热。由于热源的功率有限，随着散热面积继续增加，热电腿的温度下降趋于平缓；热电腿冷热端的温差也随着高度逐渐增加随后趋于饱和。热电腿的散热面积和散热量随高度的变化如图4(d)所示，散热面积随着高度增加而线性增加，这是由圆柱的几何性质决定的；发生在热电腿表面上的散热量随散热面积的增加而增加，表明随着高度增加，有更多的热量流入热电腿，减少了直接从热源表面散发到环境的热量损失。因此，在恒定功率的热源条件下，热电腿散热面积的增加可以有效提高热量利用率。

圆柱构型热电腿的电学输出性能如图4(e)、(f)所示。热电腿基于式(12)将两端的温差转换为电压，而平均温度的降低减小了高温对Seebeck系数的负效应，因此开路电压Voc随高度的变化趋势与温差相似。内阻Rin随高度线性增加，由于热电腿的平均温度随高度升高而降低，这降低了温度对热电材料电阻率的影响，因此随着热电腿高度增加，Rin增加速率略有减缓。热电腿的输出功率由Voc和Rin共同决定，Voc和Rin都随热电腿高度增加而增加，因此最大输出功率Pmax和功率密度Pd随高度呈现先增加后下降的趋势。Pmax在高度为25 mm时达到峰值，考虑到所占空间尺寸，Pd在15 mm时达到最佳。

特殊构型热电腿具有更大的侧面积用于散热，为了进一步减小热电腿所占空间体积并提升功率密度，特殊构型热电腿的高度设置为10 mm。并将高度为15 mm的圆柱构型热电腿的热端温度(500 K)作为恒温热源的表面温度进行后续研究。

2.2 螺旋构型热电腿

COMSOL中具有不同几何参数的螺旋构型热电腿如图5所示。螺旋构型热电腿的散热性能和电学输出性能随几何参数的变化如图6和图7所示。

如图6(a)所示，散热面积随着螺旋半径r和圈数n增加而增加，且随n的增加速度随r增加而增加，这由其几何性质决定。热电腿的冷、热端温度及温差如图6(b)～(d)所示，当热源功率恒定时，热端温度Tcold随n增加而降低，并且降低速度与r成正比，螺旋构型热电腿的热端温度低于传统圆柱构型；而当热源温度恒定时，热电腿的热端温度与热源表面温度相同。实线对应左轴刻度，表示热源功率恒定下的输出性能；虚线对应右轴刻度，表示热源温度恒定下的输出性能。在2种热源条件下，冷端温度Tcold都随着n增加而降低，并且降低速度与r成正比，这是由于侧面积增加，发生在侧面上的散热增加，从而导致冷端温度下降。当热源功率固定时，热电腿两端的温差ΔT随n增加先上升后下降，随r增加而增加，这是由于冷热端的温度都随着散热面积增加而下降，Tcold随散热面积下降的速度比Thot快，随着散热面积进一步增加，Tcold下降速度减缓，ΔT呈现略微下降的趋势；当热源温度恒定时，随着散热面积的增加，有更多的热量流入热电腿内以维持热端温度固定，因此ΔT随散热面积增加而增加，直到Tcold与环境温度相等时，ΔT趋于定值。

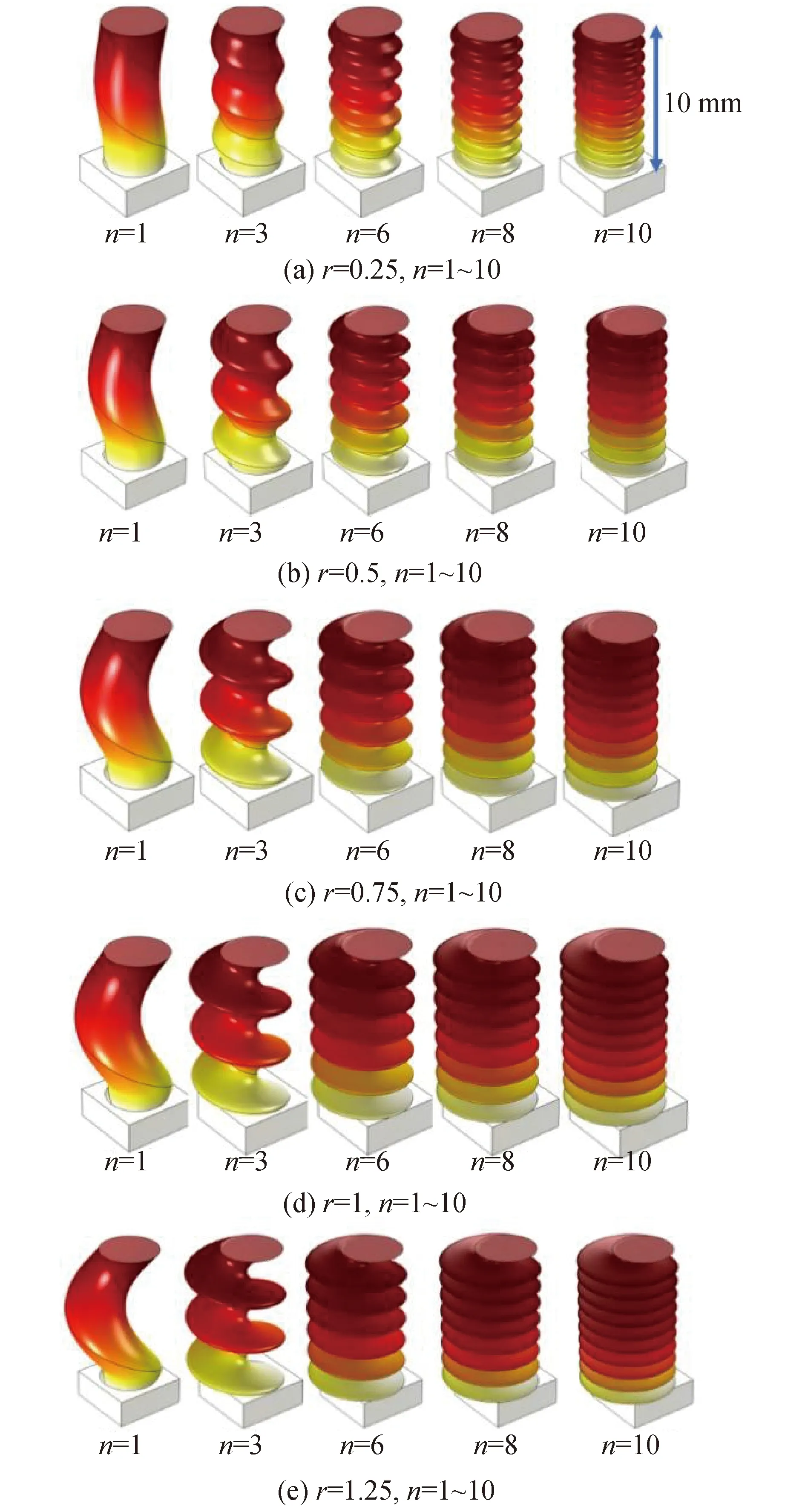
图5 COMSOL中不同几何参数的螺旋构型热电腿Fig.5 Spiral-shaped thermoelectric legs with different geometrical parameters in COMSOL

热电腿的平均温度随几何参数的变化如图6(e)所示，在2种热源条件下热电腿的冷、热端的温度都随散热面积增加而降低，平均温度也因此降低。螺旋构型热电腿在2种热源条件下的散热量如图6(f)所示，散热量随r先上升后下降，随着n增加而增加，螺旋构型热电腿的散热面积随n、r增加而增加，因此散热量随n、r增加，但是随着r持续增加，热电腿的倾角φ，如图2(b)所示也随之增加，这使得热量从热电腿的热端附近直接散发到环境中而没有流经热电腿，从而造成热量损失，因此在实际应用中，r不宜设置过大。在热源温度恒定时，为了维持热源温度恒定，有更多的热量流入热电腿，因此热电腿的散热量高于恒定功率热源。相较于传统圆柱构型热电腿，螺旋构型热电腿的散热量远高于圆柱构型热电腿，这提高了热量利用率和能量转换效率。

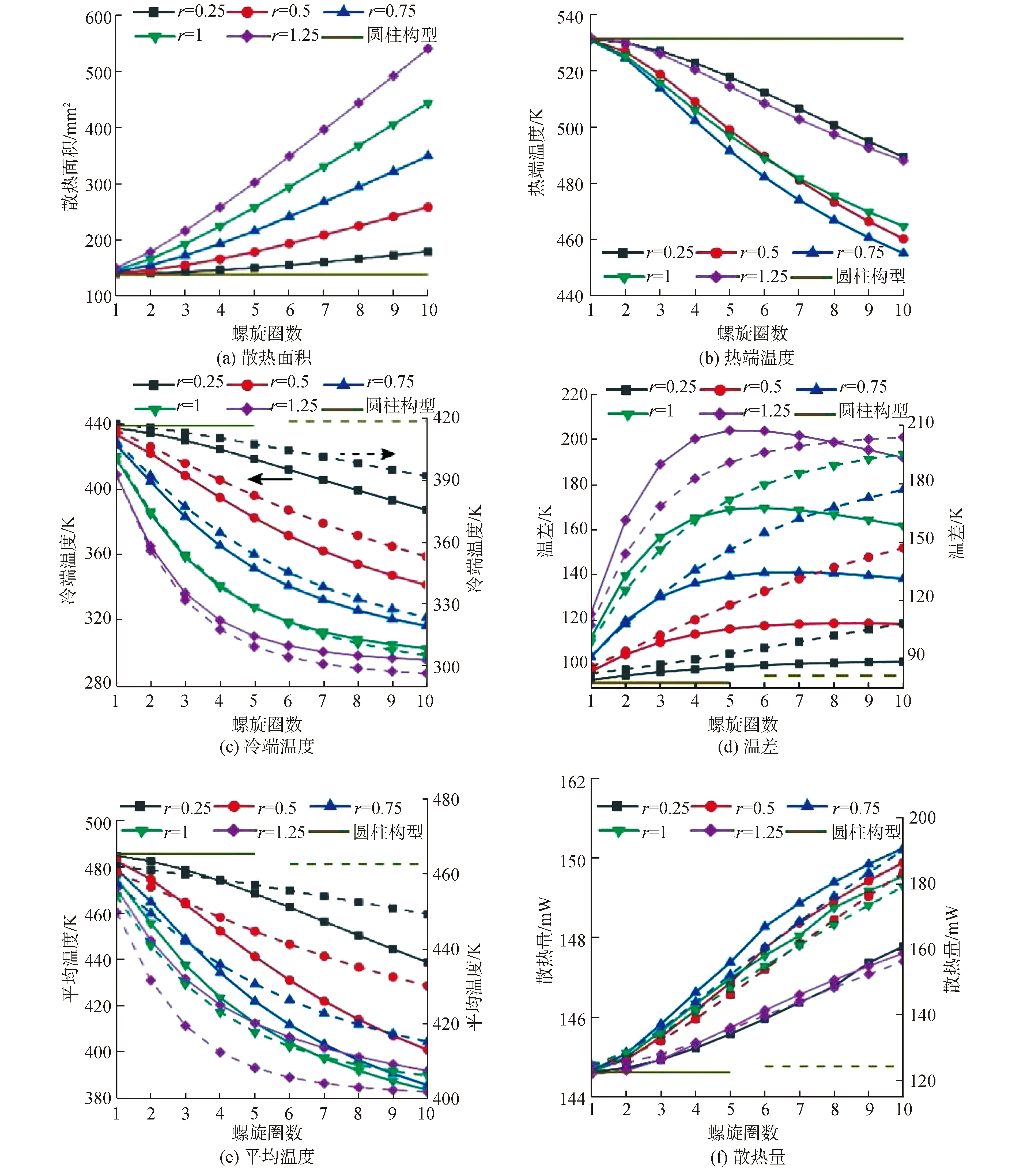
图6 螺旋构型热电腿的散热性能Fig.6 Heat dissipation performance of the spiral-shaped thermoelectric legs

螺旋构型热电腿的电学输出性能随几何参数的变化如图7所示，平均温度的降低减小了温度对Seebeck系数的负效应，Voc表现出与温差相似的变化趋势。图7(b)展示了内阻Rin随几何参数的变化趋势，n、r的增加延长了载流子在热电腿内的传输路径，Rin随n、r增加而增加，平均温度的降低同样减小了对电阻率的负效应，因此，相比于式(16)所示，Rin随n、r的增加趋势有所降低；在热源功率恒定的情况下，当r=0.25和0.5时，热电腿的几何优化降低了平均温度，且对载流子路径的延长效应不大，Rin随n增加而降低。热电腿的输出功率由Voc和Rin共同决定，螺旋构型热电腿的最大输出功率Pmax和功率密度Pd如图7(c)～(d)所示。2种热源条件下的Pmax和Pd都随n先上升后下降，即出现峰值，并且峰值所在的n随r增加而减小。相比于恒温热源条件，恒功率热源条件下Pmax和Pd的峰值所在n有所减小。

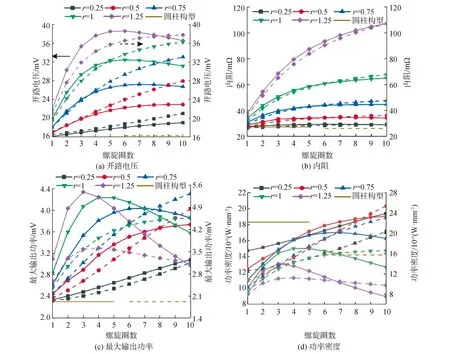
图7 螺旋构型热电腿的电学输出性能Fig.7 Electrical output performance of the spiral-shaped thermoelectric legs

2.3 轮辐构型热电腿

在轮辐构型热电腿的设计中，设置外半径r2=2.25 mm，通过调整内半径r1和轮辐数量m和张角θ来改变底面周长，并保持与对照组圆柱构型热电腿相同的底面积和质量。不同几何参数的轮辐构型热电腿如图8所示。轮辐构型热电腿的散热性能和电学输出性能随几何参数的变化如图9和10所示。

图8 COMSOL中不同几何参数的轮辐构型热电腿Fig.8 Spoke-shaped thermoelectric legs with different geometrical parameters in COMSOL

如图9(a)所示，轮辐构型热电腿的散热面积随着轮辐数量m和张角θ增加而增加，且随θ的增加速度随m增加而增加，这由其几何性质决定。轮辐构型热电腿的冷、热端温度和两端温差如图9(b)～(d)所示，图中实线对应左轴刻度，表示热源功率恒定下的输出性能，虚线对应右轴刻度，表示热源温度恒定下的输出性能。2种热源条件下Thot和Tcold都随m、θ增加而降低，并且所有几何参数的轮辐构型热电腿都低于圆柱构型；当热源功率恒定时，ΔT随m、θ增加而降低，这是由于随着m、θ增加且热源功率有限，Thot和Tcold都下降，Thot的降低速度高于Tcold，因此ΔT呈下降趋势；当热源温度固定时，Thot与热源温度相同并保持不变，Tcold随m、θ增加而下降，因此ΔT呈上升趋势。图9(e)展示了轮辐构型热电腿的平均温度随几何参数的变化趋势，在2种热源条件下，Thot和Tcold都随m和θ增加而下降，因此平均温度也呈现下降趋势。轮辐构型热电腿的散热量的变化如图9(f)，在2种热源条件下，散热量随着m、θ增加而增加；当热源温度恒定时，为了维持热源温度恒定，有更多的热量流入热电腿，因此相比于恒定功率的情况，轮辐构型热电腿的表面散发了更多的热量。在2种热源条件下，轮辐构型热电腿表面的散热量都高于传统圆柱构型，提高了热源的热量利用率。

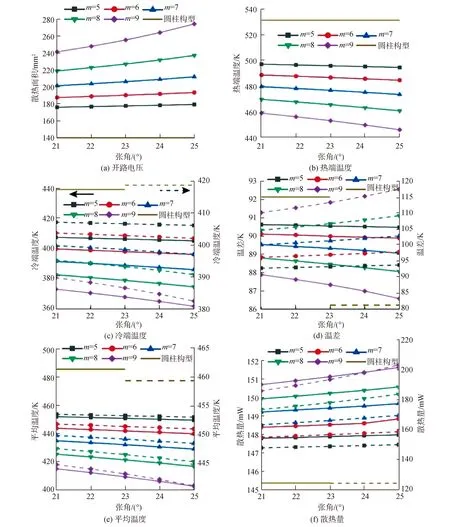
图9 轮辐构型热电腿的散热性能Fig.9 Heat dissipation performance of the spoke-shaped thermoelectric legs

轮辐构型热电腿的开路电压Voc随几何参数的变化规律如图10(a)所示，当热源功率恒定时，如上所述ΔT随m，θ增加而降低，而平均温度的降低减小了温度对Seebeck系数的负效应，在2种效应的影响下Voc随m，θ呈现先上升后下降的趋势；而当热源温度恒定时，ΔT随m，θ增加而增加，因此Voc随m，θ呈现上升的趋势。轮辐构型热电腿与圆柱构型热电腿具有相同的底面积和高度，当温度相同时具有相同的内阻Rin，由于平均温度的降低减小了温度对电阻率的负面效应，因此，在2种热源条件下，Rin随m、θ增加而降低，如图10(b)所示。轮辐构型热电腿的输出功率由Voc和Rin共同决定，变化趋势如图10(c)所示，在2种热源条件下Pmax随m和θ增加而增加，没有峰值出现。所有轮辐构型热电腿的外半径r2相同，从而具有相同的空间体积，所以功率密度Pd的变化趋势与Pmax相同。在轮辐构型热电腿的设计中，应保持m和θ尽可能大。

2.4 组合分析

相比于传统圆柱构型热电腿，2种特殊构型热电腿在具有更大的侧面积的同时也增加了所占空间体积，而在热电器件的设计中，通常将大量P/N型热电腿以π型连接的方式集成在基体上，因此有必要研究由特殊构型热电腿组成的热电器件的输出性能变化。

基于以上对单个特殊构型热电腿输出性能的研究，选取几何参数为“r=0.5，n=10”和“m=9，θ=25°”的螺旋构型和轮辐构型热电腿作为研究对象，选取传统圆柱构型热电腿作为对照组。将3种构型的热电腿以4×4的排列方式集成在方形热源表面，其中P/N型热电腿以π型方式串联连接。3种构型热电腿的组合连接方式如图11所示。在热电腿的组合设计中，相邻两个热电腿之间的空隙设置为1 mm。相比于传统圆柱构型热电腿，特殊构型热电腿占据更大的空间体积，因此由其组成的热电器件也具有更大的体积。在对特殊构型热电器件的研究中，恒温热源条件设置为500 K，恒功率热源条件设置为6.51 mW/mm2。特殊构型热电器件的输出性能如表2所示。

2种特殊构型热电腿具有更大的侧面积用于散热，进而产生更大的温差和输出电压，因此，相比于传统圆柱构型，特殊构型热电器件在2种热源条件下都产生了更大的输出电压。散热量的增加降低了特殊构型热电腿的平均温度，降低了温度对热电材料电阻率的负面影响，所以轮辐构型热电器件的内阻低于传统圆柱构型，而螺旋构型热电腿延长了内部载流子的路径，在2种效应共同影响下螺旋构型热电器件的内阻仍然高于传统圆柱构型。

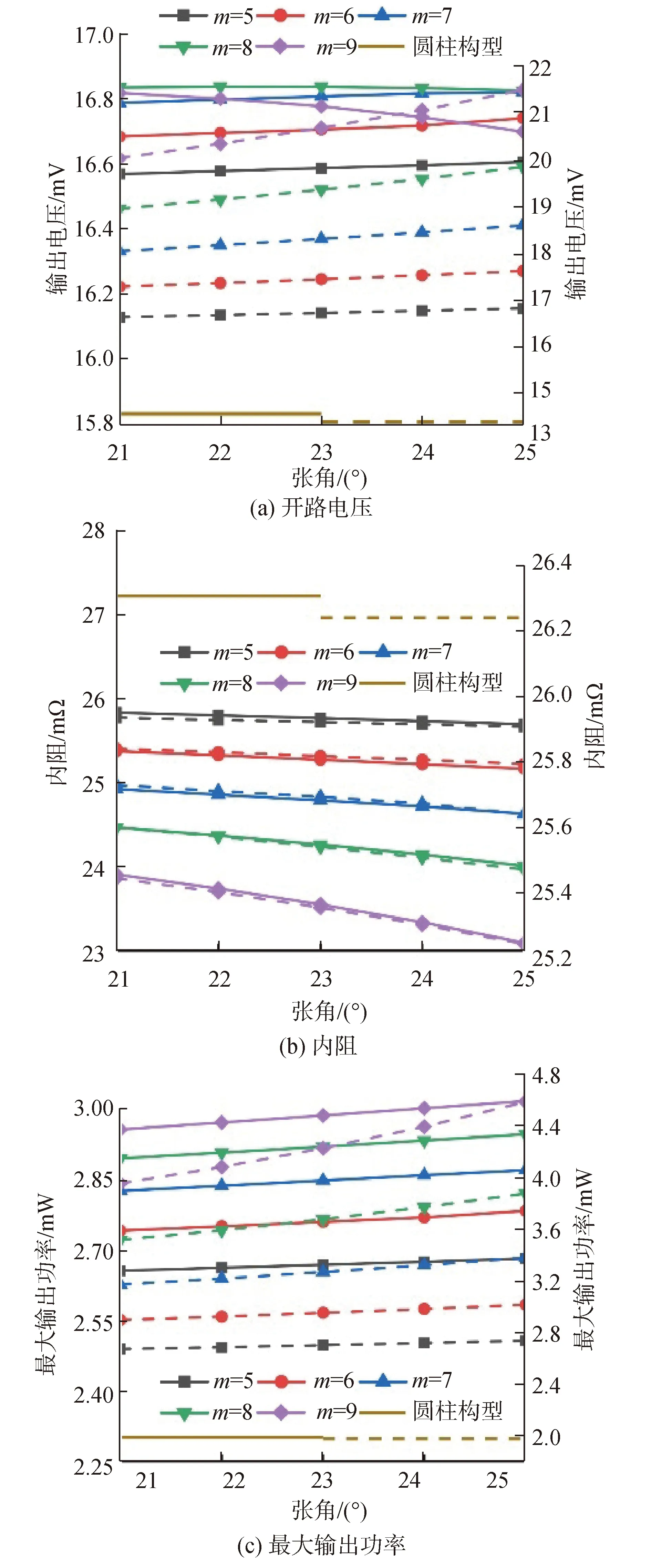
图10 轮辐构型热电腿的电学输出性能Fig.10 Electrical output performance of the spoke-shaped thermoelectric legs

热电器件的输出功率由输出电压和内阻的共同决定，经计算特殊构型热电器件的输出功率远高于圆柱构型。由于特殊构型热电器件占据更大的空间体积，计算了3种热电器件在单位面积下的功率密度，在热源功率恒定条件下，螺旋、轮辐构型热电器件的功率密度为0.175和0.142 mW/mm2，超过传统圆柱构型(0.12 mW)45.8%和18.3%；在热源温度恒定条件下，螺旋、轮辐构型热电器件超过圆柱构型50.8%和78%。特殊构型热电器件产生了更大输出电压和功率密度，因而表现出更高的能量转换效率，这也增加了热电器件的应用范围。

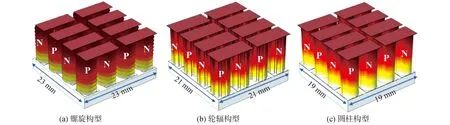
图11 3种热电腿组合示意图Fig.11 Schematic diagram of the combination of the three kinds of thermoelectric legs

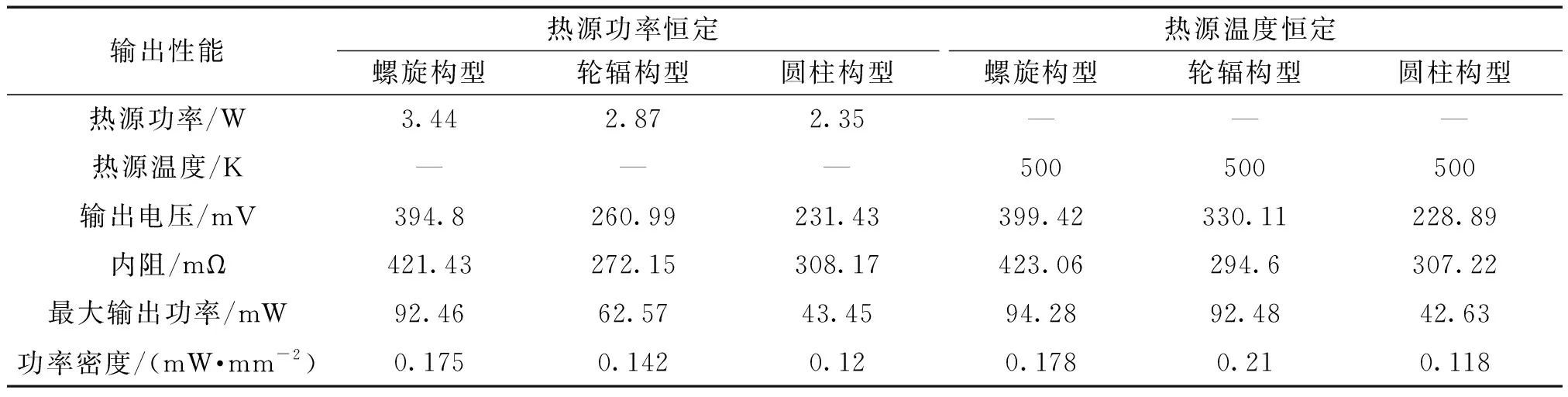
表2 特殊构型热电器件的输出性能Table 2 Output performance of thermoelectric devices with special geometrical shapes

3 结论

1)特殊构型热电腿相比于传统圆柱构型具有更大的侧面积，散热效果更强，能够产生更大的温差。但是侧面积增加的同时，也会占据更大的空间体积，这在一定程度上也限制了特殊构型热电腿集成在热电器件内的数量。

2)采用特殊构型的热电腿设计还可以降低热电材料的自身温度，减弱高温对材料性能引起的负面效应。研究结果表明在热源功率恒定的情况下，螺旋构型热电腿的输出性能更佳；在热源温度恒定的情况下，轮辐构型热电腿的输出性能更佳。

3)本文所开展的研究与讨论是针对GPHS热源和热源表面温度为500 K的2种典型代表的热源条件，所涉及的热电腿构型限于螺旋、轮辐和圆柱3类，并在此基础上分析了特殊构型热电腿的输出性能随几何参数的变化规律。

在后续工作中，会根据热源的功率、热电器件内热端的热量分布等更贴合实际的情况，进一步优化热电腿的几何参数，使热电器件的输出性能达到最佳。本文关于2种特殊构型热电腿的设计方法及其相关性能结果，对小型同位素温差电池的设计制备及在不同应用场景下的热电器件的结构设计方案研究提供了一定的参考借鉴价值。