目标偏置双向RRT*算法的机器人路径规划

刘奥博，袁 杰

新疆大学 电气工程学院，乌鲁木齐 830047

机器人路径规划可以定义为找到一条从起始点到目标点的无碰撞可行路径的过程。基于采样的算法已经应用于解决高维规划问题，且计算效率较高。

LaValle提出经典的基于采样的RRT算法[1]，对整个环境空间进行均匀随机采样，具有概率完备性，但是该算法只通过一棵随机树对空间进行探索，在复杂环境中会消耗大量时间。Kuffner等[2]提出的RRT-connect算法，采用双向搜索思想在起点和目标点同时生成两棵随机树。李成雷等[3]提出改进的RRT-connect算法，在采样过程中引入转角约束，以减少搜索节点，但上述算法随机树的生长是发散的，在不必要的区域进行采样会耗费大量的时间，规划出的路径也不是最优的。Karaman等[4]提出的RRT*算法，当迭代次数足够多时，可找到一条最优或接近最优的路径，但是搜索时间大大增加。Jordan等[5]提出双向版的RRT*算法，称为B-RRT*算法，搜索速度加快，但在复杂环境下计算节点量较大。Qureshi等[6]提出智能双向搜索的IB-RRT*寻优算法，专用于复杂环境搜索，但是采样节点的扩展是随机的，在无用区域采样造成不必要的时间消耗。为避免随机树扩展过程的随机性，LaValle等[7-11]采用目标偏置思想，使随机树朝目标点方向生长。Nasir等[12]提出智能偏置采样的RRT*-smart算法，但不同环境下需手动调节偏置比，自适应性较差。Liu等[13]提出将目标偏置与曲线平滑结合的GB-RRT算法，减少搜索时间，但规划路经转折处较多，路径距离较长。刘建宇等[14]提出改进的RRT*-connect算法，在目标偏置采样基础上对采样区域进行约束，但当可行路径需经过约束区域之外时，算法不能确保找到可行解，有待进一步完善。

基于上述研究，本文针对较复杂环境下移动机器人的路径规划问题，提出了一种目标偏置双向RRT*（goal biased bidirectional RRT*，GBB-RRT*）算法。首先借鉴双向搜索思想，从起始和目标位置同时构造两棵随机树，每次迭代，两棵随机树都进行新节点的扩展，加快随机树扩展速度，减少搜索时间。在采样过程中，在一定概率下将两棵随机树各自目标点作为采样点，引导两棵随机树以一定的概率朝各自的目标点方向生长，减少在无用区域的搜索，提高搜索效率，减少时间消耗。针对规划得到的初始路径曲折问题，设计一种逆向寻优结合转角约束路径简化方法，然后采用B样条曲线对简化后的路径进行处理，生成机器人可跟踪执行的光滑路径。通过仿真复杂环境实验对比，验证了所提算法的快速性和有效性。

1 B-RRT*算法

B-RRT*算法采用贪婪启发式进行两棵随机树的连接，既具有概率完备性，且已证明具备渐进最优性，相比RRT*算法额外增加了Connect()函数，算法1给出了BRRT*算法的伪代码。

B-RRT*算法以起始点xinit和目标点xgoal为根节点生成两棵随机树Ta、Tb。首先扩展随机树Ta，初始阶段与RRT*算法完全相同，在配置空间中随机采样得到xrand，然后执行算法2。

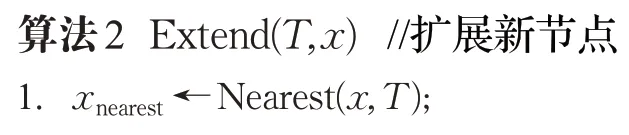
搜索随机树Ta中距离最近的树节点xnearest，其延伸步长距离得到新节点xnew。以xnew为圆心r为半径的圆确定邻域集合Xnear，将从根节点经过Xnear中节点到达xnew的无碰撞路径代价与从根节点经过xnearest到达xnew的路径代价比较，确定路径代价最小的节点为xnew的最佳父节点。然后将路径与新节点xnew插入随机树，对Xnear中每个节点进行重布线。在将新节点xnew插入随机树Ta后，接下来和RRT*有所不同，执行函数Connect(xnew,Tb)，返回无碰撞可行路径代价θnew，若θnew＜θbest，则两棵树连接成功。迭代结束时通过SwapTrees(Ta,Tb)交换两棵随机树，在下次迭代中，进行随机树Tb的扩展，执行和随机树Ta相同的扩展过程。

2 目标偏置双向RRT*算法

机器人在存在大量障碍物等复杂环境中进行路径规划时，使用RRT*和B-RRT*算法存在搜索时间长、采样点随机性大和规划路径曲折的问题。基于上述研究，本文提出了目标偏置双向RRT*算法（GBB-RRT*）。主要改进是一次迭代中同时扩展两棵随机树、引入目标偏置策略优化采样过程。算法3给出了GBB-RRT*算法伪代码。

图1为GBB-RRT*算法扩展示意图。如图1（a）和算法3所示，算法在每次迭代中，以起始点xinit和目标点xgoal为根节点生成两棵随机树Ta、Tb，这两棵随机树将同时在自由环境中扩展，以随机树Ta向其目标点xgoal方向扩展过程来说明。首先，通过算法4生成新节点

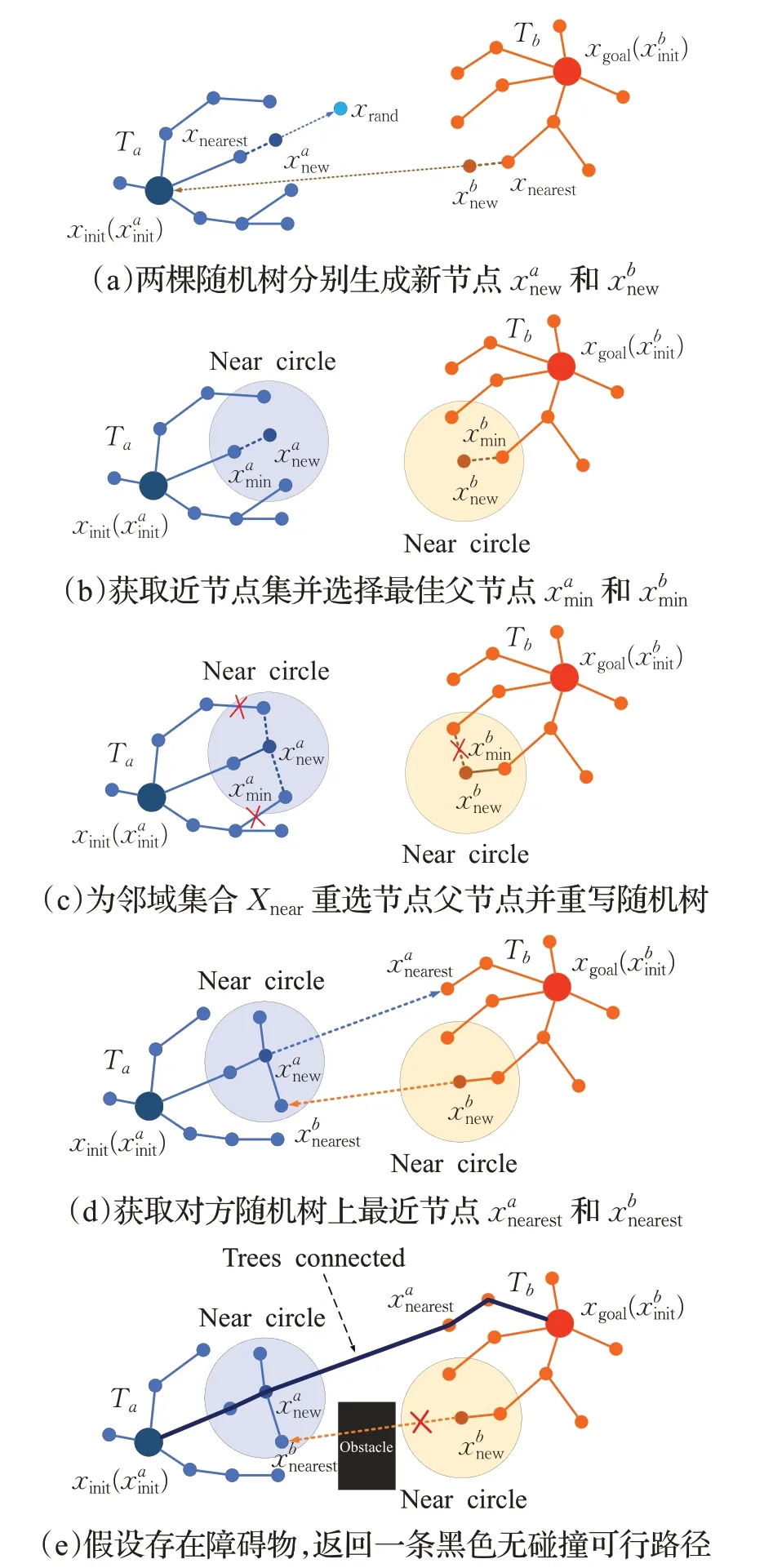
图1 目标偏置双向扩展随机树Fig.1 Goal biased bidirectional RRT*

算法4为改进的扩展函数Extend*()，引入目标偏置思想确定采样点：

如式（1），设定一个目标偏向阈值Ptarget（0.6），然后按均匀概率分布随机获取一个概率值P（0-1），若其值大于阈值，则将目标点xgoal作为采样节点；若小于阈值，则将SampleFree()函数产生的随机点作为采样节点。图1中树Ta将随机点xrand作为采样节点。

3 路径简化与平滑处理

在存在大量障碍物等较复杂环境中，本文所提GBB-RRT*算法规划出的初始路径仍然曲折。针对这个问题，设计一种逆向寻优结合转角约束路径简化方法。与文献[15-17]采用正向简化方法相比，本文采用正向遍历、逆向简化的方法。从起点开始若有节点与目标点之间连线可无碰撞直达，则直接连接该节点与目标点，省去后面节点的简化，减少时间消耗，对狭窄通道、大量障碍物等复杂环境有快速通过性，简化路径更短。与文献[18]在随机树生长过程引入转角约束相比，本文在进行简化路径时引入转角约束，可在满足机器人约束条件的同时使简化后路径长度更短，然后采用B样条曲线对简化路径进行平滑处理，生成移动机器人可跟踪执行的光滑路径。

3.1 路径简化

逆向寻优结合转角约束路径简化方法如图2所示。

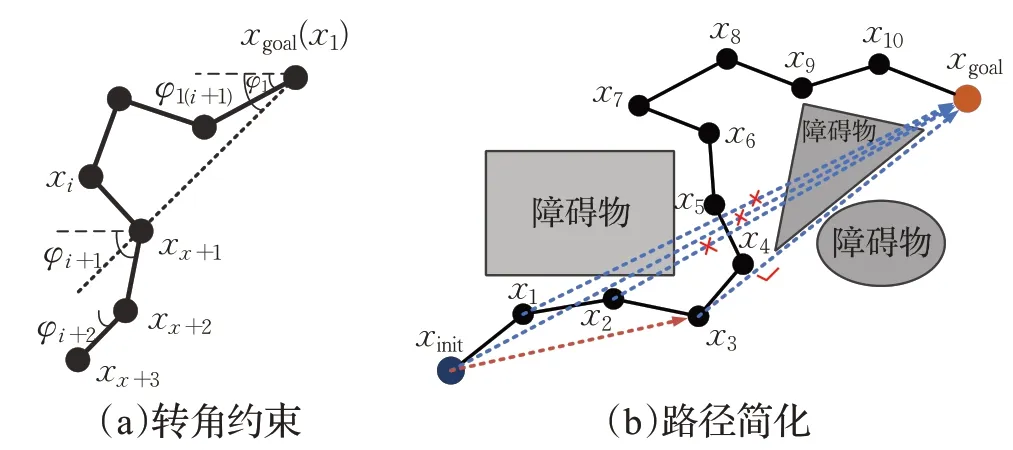
图2 转角约束与路径简化示意图Fig.2 Corner constraint and path simplification

图2（a）为转角约束示意图，以xgoal(x1)为起点，其中xi+1是正向遍历时第一个和xgoal连线不与障碍物碰撞的路径点。φ1为xgoal(x1)对应的初始角度，φ1(i+1)为目标点xgoal与路径点xi+1连线与x轴的夹角，φi+1为路径点xi+2和xi+1连线与x轴的夹角，φi+2为路径点xi+3和xi+2连线与x轴的夹角。然后判断上述参数是否满足约束条件：

φmax为最大转角约束，如果公式（2）成立，则可将xgoal和xi+1之间的节点剪除。

图2（b）为路径简化示意图。其中xinit为初始点，xgoal为终点，xi为可行路径上的节点，黑实线为规划得到的初始可行路径。对初始可行路径：

步骤1采用正向遍历方法，确定首个无碰撞点。首先从起点xinit开始判断与目标点xgoal之间是否存在障碍物。若无障碍物，则直接连接起点与目标点即为最优简化路径；若存在障碍物，进行下一个节点x1与目标点xgoal碰撞检测。从图2（b）可看出，xinit、x1、x2和xgoal连线均与障碍物碰撞，x3为初始路径正向遍历时第一个与目标节点xgoal无碰撞的路径节点。

步骤2逆向寻优，确定简化路径节点。简化路径的第一个节点为xgoal，由步骤1确定的节点x3，其与目标点xgoal之间满足转角约束，所以x3为简化路径第二个节点。同时将x3定义为新的目标节点xgoal。

重复步骤1、2，直到完成对整条初始可行路径的简化。图2（b）中xinit和新目标点x3连线不与障碍物碰撞，且满足转角约束，因此，xinit为简化路径第三个节点。简化后的路径即图2（b）中从起点xinit经过x3到目标点xgoal的路径。具体的流程如图3所示。

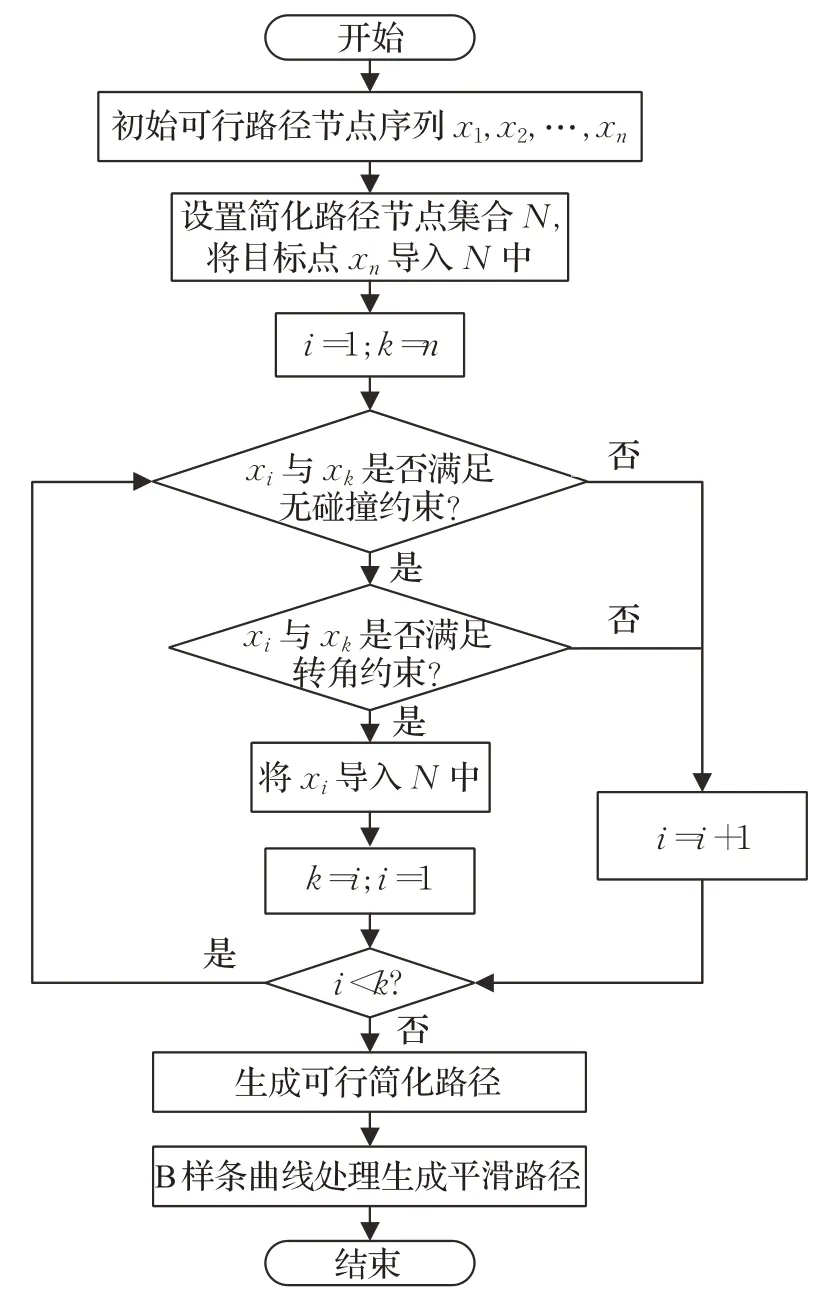
图3 路径简化与平滑处理流程图Fig.3 Flow chart of path simplification and smoothing

3.2 平滑处理

对上述简化方法生成的仍然曲折的简化路径，考虑对简化路径的平滑要求，采用二次B样条曲线对简化路径进行平滑处理。由于B样条曲线的连续性和局部性特点，可在不改变整条路径形状的情况下，只在局部对简化路径进行平滑处理。如图4（a）中蓝色实线为GBBRRT*规划得到的初始可行路径；图4（b）中绿色实线为简化后路径；图4（c）中红色实线为B样条曲线拟合生成的平滑路径。

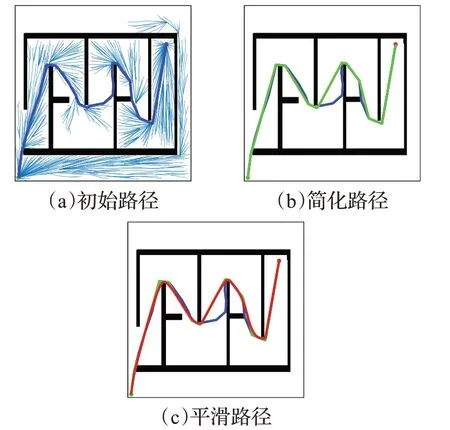
图4 路径简化与平滑处理效果图Fig.4 Effect picture of path simplification and smoothing

4 仿真实验对比分析

在笔记本电脑上使用Matlab R2018a对本文所提算法进行仿真实验验证。计算机为Win10系统，处理器Intel Core i5-4120M，主频2.6 GHz，运行内存8 GB。

4.1 仿真实验

为了验证所提的GBB-RRT*算法具有更好的性能，本文将RRT*、B-RRT*和GBB-RRT*算法在3种二维仿真复杂环境下进行对比实验，地图大小均为500 m×500 m。由于在复杂环境下RRT*找到初始可行路径需经过大量迭代，时间成本消耗过大，为了更好展示这两类算法在搜索速度上的区别，下面只描述B-RRT*和GBB-RRT*的对比实验。最大采样点(N)个数限制为1万个。在三种环境下均进行50次重复实验。表1列出了两种算法找到初始可行路径解的平均扩展节点数、平均时间、平均初始路径和简化路径长度。

图5为存在大量随机障碍物环境，图6为狭窄通道较多的迷宫式复杂环境。起点（10，10），终点分别为（490，490）和（460，460）。从图5和图6中可以明显看出，由于B-RRT*采样随机性，随机树更多地往碰撞概率小的区域扩展，生长较为发散。由于GBB-RRT*引入了目标偏置策略，使随机树扩展具有一定的方向性，有向目标点生长的趋势，有更大的概率对内部通道狭窄区域进行探索，能更快速地通过通道狭窄区域，减少对不必要区域的探索，搜索时间更少，路径长度更短，规划出的初始可行路径质量更高。如表1所示，在第一种大量障碍物环境下找到初始可行路径时，GBB-RRT*算法平均扩展节点和初始路径长度比B-RRT*分别减少10.52%和1.58%。GBB-RRT*平均搜索时间（0.768 7 s）比B-RRT*（1.296 9 s）缩短40.72%。在第二种狭窄通道迷宫环境下找到初始可行路径时，GBB-RRT*平均扩展节点和初始路径长度比B-RRT*分别减少14.77%和3.37%。GBB-RRT*平均搜索时间（0.557 s）比B-RRT*（1.006 4 s）缩短44.65%。

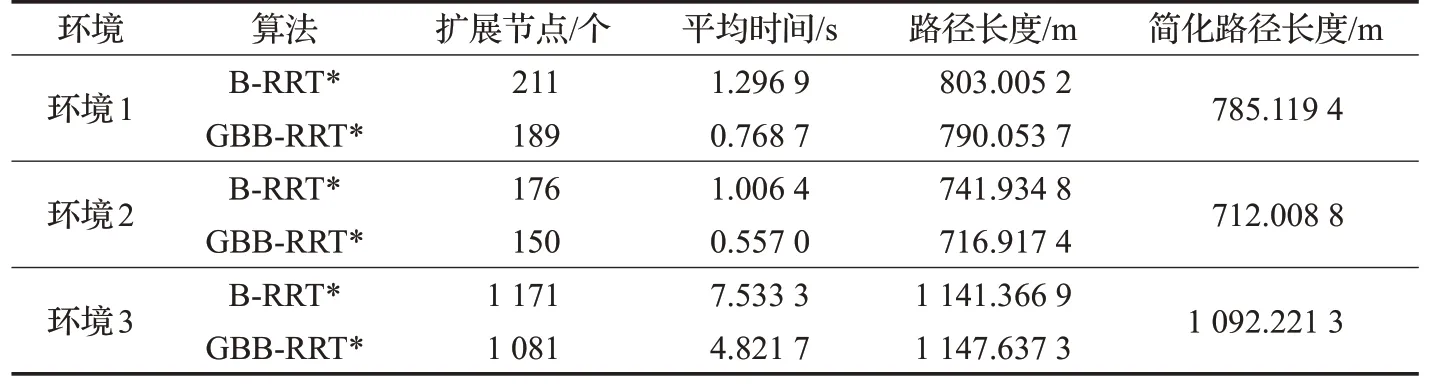
表1 找到初始可行解的实验结果Table 1 Experimental results of finding initial feasible solution

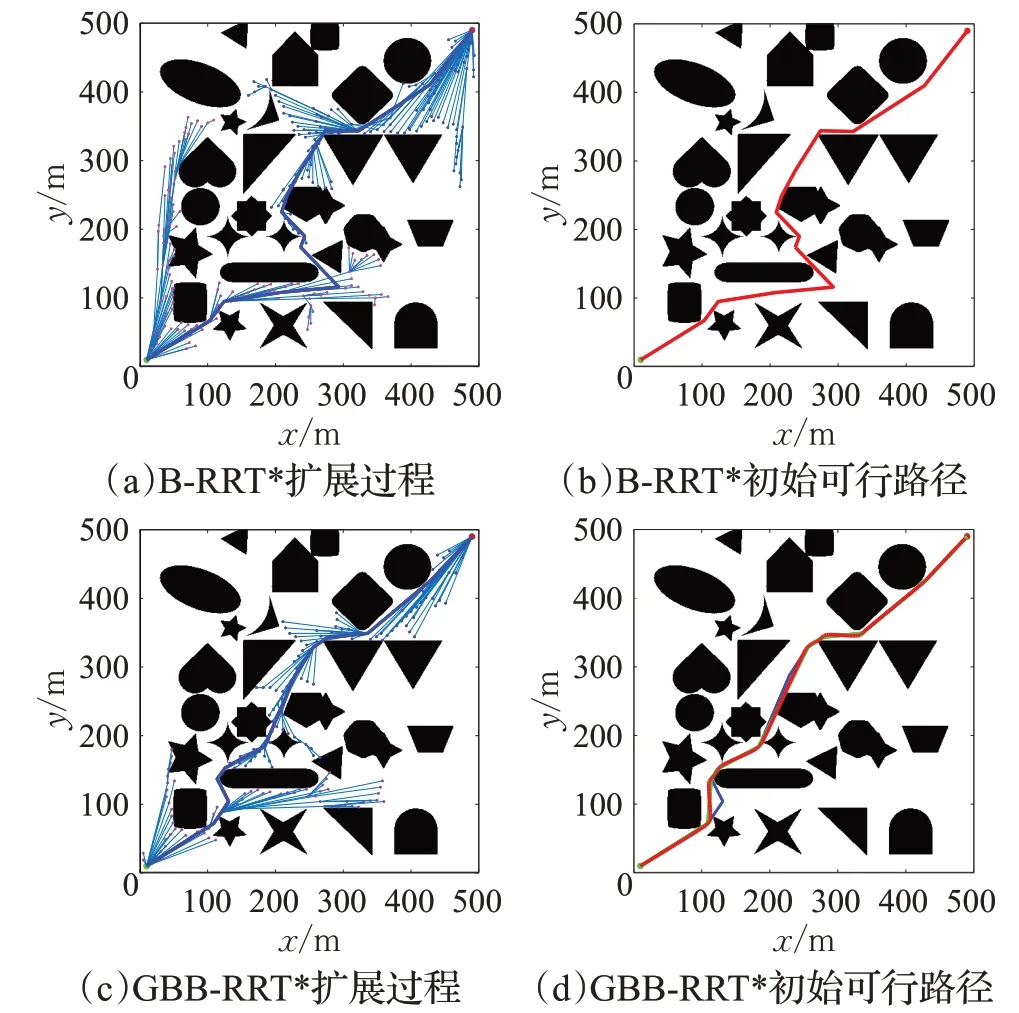
图5 大量障碍物环境规划结果对比Fig.5 Comparison of environmental planning results for a large number of obstacles

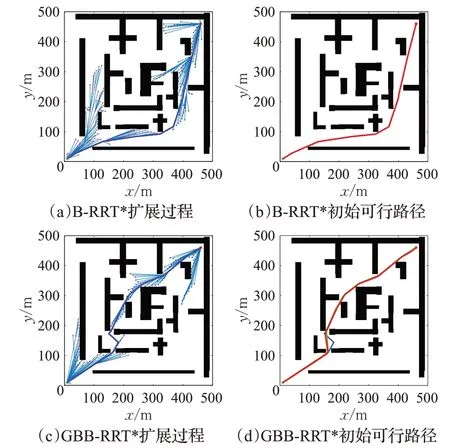
图6 狭窄通道迷宫环境规划结果对比Fig.6 Comparison of labyrinth environmental planning results for narrow passage

图7是非常具有挑战性的单通道迷宫环境，起点（10，10），终点（390，430）。特点是只有一条可行路径通道，且通道转折多，对算法快速通过性要求较高。由于B-RRT*和GBB-RRT*经过大量迭代后对配置空间的探索相似，所以扩展节点数和路径长度很接近。不同的是GBB-RRT*算法具有一定方向性，能以更短的时间逃离迷宫。如表1所示，GBB-RRT*算法平均搜索时间（4.827 1 s）比B-RRT*（7.533 3 s）缩短35.99%。

图5～7的图（d）中蓝色实线为初始路径，绿色实线为简化路径，红色实线为光滑路径。从图5（d）、图6（d）和图7（d）可以看出，算法规划出的初始可行路径较为曲折，采用所设计的路径简化方法对初始路径进行简化，然后采用B样条曲线进行平滑处理后，路径明显更为简短和光滑。尤其对图7环境，初始路径曲折较多，由表1可知，简化前B-RRT*和GBB-RRT*规划路径相差不大，但经过简化处理后路径长度较B-RRT*缩短4.3%。所以，本文所提路径简化平滑处理方法效果良好，并且是十分必要的。

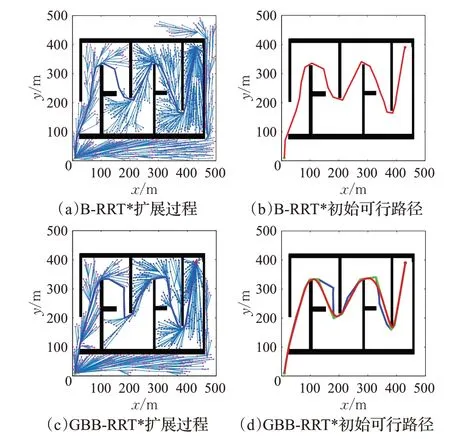
图7 单通道迷宫环境规划结果对比Fig.7 Comparison of single channel maze environmental planning results

通过表1可以看出，虽然B-RRT*算法能在较短时间找到初始可行路径，但是时间耗费很大，规划路径长度也更长。本文所提出的目标偏置双向RRT*（GBBRRT*）算法在3种复杂环境下，找到初始可行路径解所需的扩展节点更少、搜索时间更短，经过路径简化与平滑处理方法处理后，路径长度更短、更光滑。

4.2 对比分析

图8为上述实验在找到初始可行路径的数据对比柱状图，为了反映算法的规划效率和规划路径质量，从平均扩展节点、平均搜索时间、平均路径长度和简化处理后路径长度四个指标进行评价。

从图8（a）、（b）中可以看出，与B-RRT*算法相比，本文所提GBB-RRT*算法有较少的扩展节点、较短的搜索时间，特别是搜索时间大大减少。图8（c）中绿色为简化后路径，路径长度明显缩短，说明了路径简化与光滑处理的必要性和有效性。

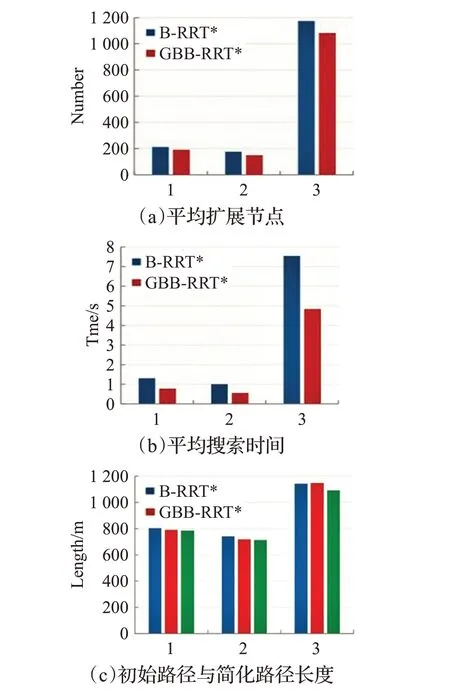
图8 三种环境实验数据对比Fig.8 Comparison of experimental data in three environments

5 结束语

本文针对较复杂环境下采用RRT*算法和B-RRT*算法进行移动机器人的路径规划，存在搜索时间长、采样效率低和规划路径曲折的问题，提出了目标偏置双向RRT*（GBB-RRT*）算法。将双向搜索与目标偏置思想相结合，加快随机树的生长速度，提高算法搜索效率，大大减少搜索时间。所设计的逆向寻优结合转角约束路径简化方法，可结合B样条曲线生成机器人可跟踪执行的光滑路径。通过在三种仿真环境下与B-RRT*算法进行对比实验，结果表明所提GBB-RRT*算法搜索时间缩短40%左右、扩展节点减少10%左右，结合路径简化方法后路径长度缩短3%左右。证明了所提算法具有一定的优越性和有效性。