面向非正交多址的车联网中资源优化方案

张海波，陶小方，刘开健

重庆邮电大学 通信与信息工程学院 移动通信教育部工程研究中心，移动通信技术重庆市重点实验室，重庆 400065

随着物联网的快速发展，计算密集型移动应用日益遍及，现有的移动用户设备在应用处理或能量提供方面已无法满足相应的挑战。同时，在移动视频、在线社交媒体等的带动下[1]，大数据流量呈指数级增长，使得移动网络面临计算限制。虽然无线频谱已被诸如超密集网络充分利用，但回程可能成为新的瓶颈，无法负担巨大的业务流量[2]。未来的无线网络有望支持大量计算密集型和延迟敏感的应用，如虚拟现实和自动驾驶。由于大多数移动设备的计算能力和功耗有限，移动边缘计算（mobile edge compution，MEC）被认为是一种很有效的加强计算服务的方法[3]。

通过向附近的MEC服务器卸载负载，计算密集型应用程序可以有效地执行。通过有效卸载和资源分配[4]，可以在很多方面提升系统性能，如降低处理延迟和能耗，或提高能源效率等。由于车辆移动方向和速度的随机性使得动态资源调度变得非常复杂和具有挑战性。因此，在车联网络中，卸载和缓存决策的制定以及计算和缓存资源的优化分配至关重要。目前大量的文献已经研究通过优化无线电和计算资源制定有效的任务卸载策略。在带宽有限的情况下，文献[5]提出了基于图转换的任务负载分配策略和基于背包的虚拟池资源分配策略。文献[6]研究了无线MEC中的任务卸载和资源分配问题，以最大限度地减少时延，同时节约用户设备的电池电量。文献[7]中为了最大限度地提高用户的任务卸载收益，研究了任务卸载和资源分配问题。

为了减轻大数据带来的沉重的流量负担，提高互联网内容的传输质量，将流行的内容更贴近用户，从而为用户提供缓存的内容，而不是从远程服务器下载的内容。通过将计算任务所需的数据卸载到边缘服务器并在边缘服务器上进行缓存，可以显著降低计算重复任务造成的延迟[8]。考虑到小蜂窝网络的回程容量非常有限和基于其流行程度的缓存文件，文献[9]的作者观察到通过在小基站上缓存可以减少回程流量负载。许多研究致力于内容缓存策略。根据高速缓存车辆和移动用户之间的相关性，文献[10]的作者通过建立网络能耗最小化的优化模型，研究了内容中心网络中车辆缓存方案的有效性。文献[11]提出了计算卸载决策、资源分配和内容缓存策略作为一个优化问题，并考虑了网络的总收益。

虽然在计算卸载和内容缓存方面进行了大量的研究工作，但很少共同考虑和解决计算卸载和缓存的能耗。此外，在现实通信系统中，车辆产生的移动流量通常是随机动态到达的，而上述工作主要是在静态网络中进行计算卸载和内容缓存，没有考虑数据和缓存队列的动态特性以及动态优化数据流量。因此，不可预测性会难以获得上述文献的系统性能。

近年来，非正交多址接入（non-orthogonal multiple access，NOMA）技术在提高网络频谱效率方面显示出了巨大的潜力。与传统的正交多址（orthogonal multiple access，OMA）网络不同，NOMA网络允许多个用户通过不同的功率级别共享相同的频率资源，接收机采用连续干扰消除（successive interference cancellation，SIC）技术进行用户检测。然而，目前大多数MEC卸载缓存方法通常考虑的是OMA[12]。由于NOMA优于OMA的优点，预计将在MEC系统中应用NOMA，为了进一步提高卸载性能，研究了文献[13]中基于上下行NOMA的多用户卸载系统。文献[14]研究了一种非正交多址辅助移动边缘计算系统，优化该系统的功耗和时延。然而，基于NOMA的MEC任务卸载的好处不止这些。目前对基于NOMA的MEC系统通常忽略了缓存数据包下载这一阶段，将NOMA应用于基站的下行数据包传输，制定缓存策略和缓存资源分配可以进一步提高系统性能。

本文针对MEC端总的能量消耗最小化问题，研究了在NOMA协助的车辆边缘计算网络下构建计算卸载和内容缓存队列。然而，与卸载非车辆用户不同，由于车辆环境的高度动态、无线信道的快速波动等因素，在处理车辆用户时考虑随机流量到达和队列稳定性，通过联合优化计算卸载决策和内容缓存决策，以及计算和缓存资源的分配，将其定义为一个随机优化问题。利用李雅普诺夫优化理论，提出求解该问题的动态联合计算卸载、内容缓存和资源分配算法。由于优化问题是混合整数非线性问题，将其解耦为两个独立的子问题，并用0-1整数规划和线性规划方法求解这两个子问题，得出最优解。

1 系统模型

1.1 系统分析

如图1考虑一个MEC服务器和K个用户的基于NOMA的车辆边缘计算网络下任务卸载和缓存场景。每个基站上都部署了MEC服务器，并且基站通过有线回程连接到核心网络。每个车辆用户都有一个需要处理的计算密集型应用程序，同时它也可以向核心网络中的内容服务器请求内容。

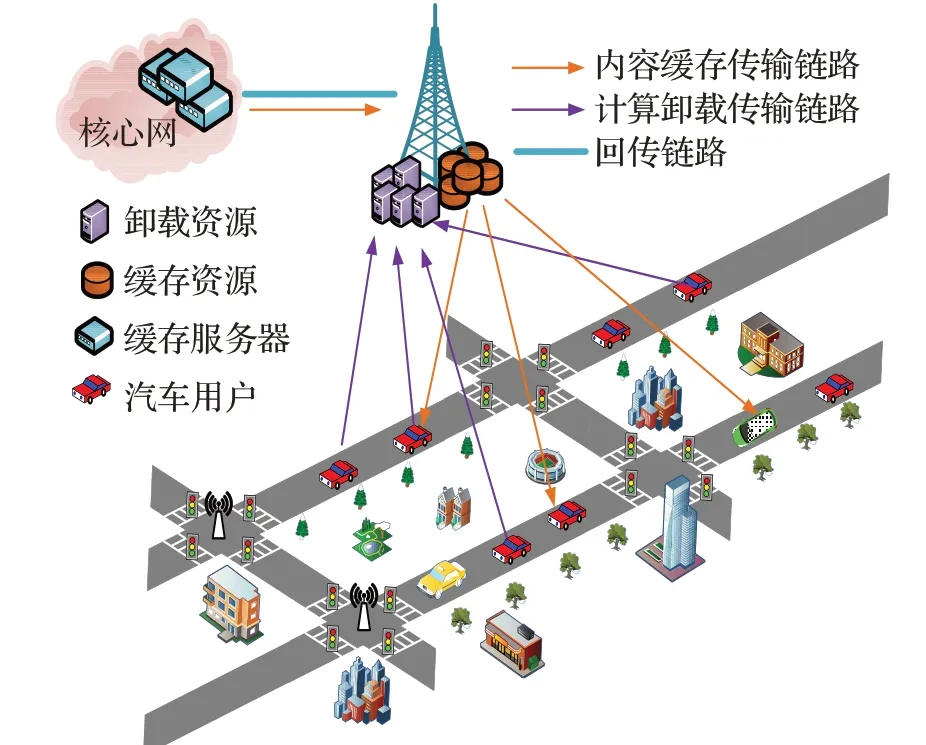
图1 系统模型图Fig.1 System model diagram

本文只研究单一基站下的计算卸载、内容缓存和资源分配，不考虑不同基站之间的切换问题。假设该系统具有固定时隙t∈{0,1,2,…}，大小为τ=10 ms。假设车辆以20 m/s平均速度移动，基站的平均覆盖区域为320 m，在一个时隙内，由于车辆的移动距离为0.2 m，可将这个时隙内网络假设为准静态的，其中车辆和无线信道在这个时隙中保持不变。但是在不同时隙，车辆在基站覆盖单元中的位置发生变化，所以对于整个计算卸载或缓存期间无线信道是变化的。

在每个时隙中，当一个车辆用户请求处理应用程序时，可以在本地处理应用程序，也可将其卸载到MEC服务器执行。当多个车辆用户需要进行卸载或者缓存时，应向每个用户合理分配计算和缓存资源。另一方面，研究了在内容中心网络（content centric network，CCN）中的边缘缓存，CCN中包含兴趣包和数据包[15]。每个用户发送命名信息的兴趣包，基站接收兴趣包并且内容服务器应决定缓存请求是否被缓存，需要多少资源。如果在高速缓存服务器中缓存具有车辆所请求内容，基站直接将数据包交付给用户。

1.2 通信模型

假设车辆用户到MEC服务器的上行信道为频率平坦的块衰落瑞利信道。车载设备与RSU之间的路径损耗建模为( Jk(t))α,其中Jk(t)为t时刻MEC服务器与车辆用户的距离，α为路径损失系数，β为信道衰落系数。信道增益是距离变化的函数表示为Hk(t)=( Jk(t))αβ2,距离随时间t变化，可以表示为：

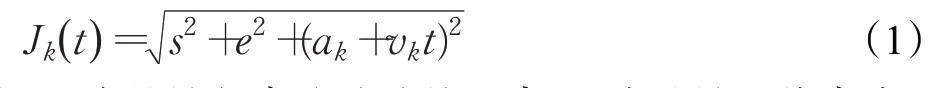
其中，s为基站与高速公路的距离，e为基站天线高度，ak为车辆用户k沿公路以速度vk单向移动的初始值。

在卸载阶段所有车辆用户依靠上行NOMA方案将任务传输到MEC服务器。按照用户信道功率增益大小排序为H1(t)≤H2(t)≤…≤HK(t)。然后，基站利用连续干扰抵消（SIC）技术从用户中解码计算任务。根据SCI原理，采用固定的译码顺序来处理和减少信令开销。假设上行解码顺序总是从信道增益较好的用户到信道增益较差的用户，因此在上行链路中第k个用户的传输速率为：

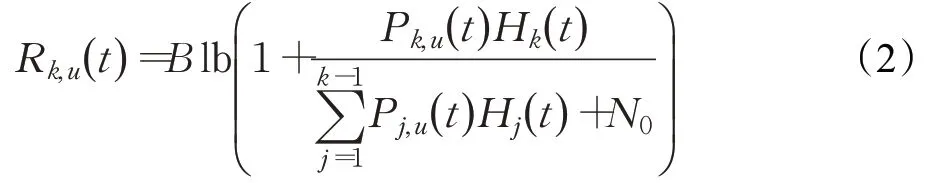
假设信道增益Hk(t)=( Jk(t))αβ2,Jk(t)为t时刻MEC服务器与车辆用户的距离，α为路径损失系数，β为信道衰落系数。其中B为频谱带宽，Pk,u为在时隙t内车辆k发射功率，N0为高斯白噪声功率谱密度。

在缓存阶段基站利用下行NOMA信道将数据包传送给请求车辆用户，下行信道增益与上行信道增益相同，译码顺序服从信道增益的递增顺序。其中Pk,d为在时隙t内基站发射功率，因此在下行链路中第k个用户的可用下行速率为：

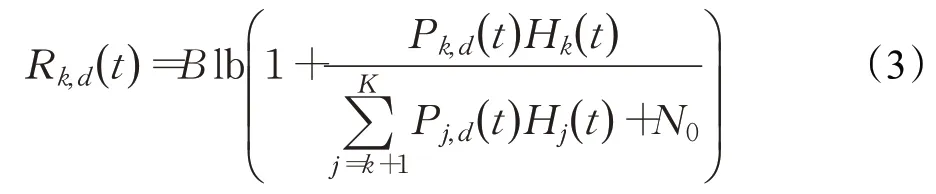
1.3 卸载模型

其中，fm,k是MEC服务器分配给移动车辆的CPU周期数，κ为MEC服务器上的有效切换电容。相应的MEC服务器端因卸载产生的能量消耗为：

1.4 缓存模型

在每个时隙内，每个车辆用户可以向内容服务器请求内容。对于每个移动用户的内容请求，MEC服务管理器应该决定是否应该将内容缓存到MEC中，以及根据系统效用为每个缓存的内容分配多少缓存资源。定义yk(t)为车辆用户缓存决策，yk(t)为1表示MEC服务器缓存车辆用户请求的内容；yk(t)为0表示MEC服务器不缓存车辆用户请求的内容。同时用一组相同大小的文件片段F={F1,F2,…,FNf}来表示所请求的移动数据，其中Nf表示片段总数并且所有文件片段都有不同的请求概率。利用广泛使用的Zipf分布模型来计算片段的流行度，片段Fj被请求的概率为：

其中，φ为值为0.56的Zipf分布指数。

假设MEC服务器上针对每个车辆都有一个缓存队列，表示为Zk(t)。请求到达率为Ak(t)并满足0≤Ak(t)≤Akmax(t)，即动态缓存队列Zk(t)由下面公式构成：

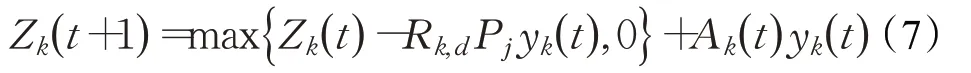
为了表示MEC服务器在缓存时消耗的传输能量，采用了线性能量消耗模型[15]，其中ωmt是基站传输的能量消耗速率，值为0.5×10-8J/bit，因此MEC服务器缓存所耗费的能量为：

2 问题的形成与转化

2.1 问题形成

建立的目标规划问题包括：制定一个多用户的NOMA场景，考虑卸载和缓存决策以及资源分配，以在MEC服务器端的队列稳定性条件下MEC服务器端消耗的平均能量最小为目标，获得最优卸载策略、缓存策略、计算资源和缓存资源分配，使得系统总能耗最小。

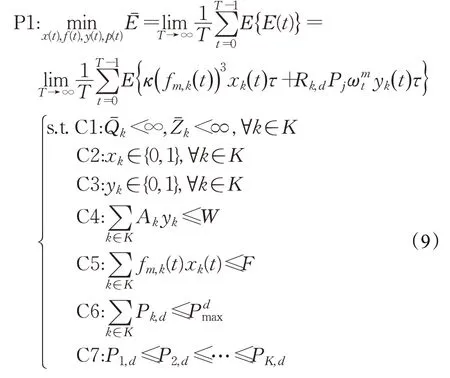
上述中F和Pmax为MEC端总计算资源以及最大发射功率，W为MEC缓存最大存储容量。其中，C1确保系统是稳定的；C2和C3是计算卸载和内容缓存策略的变量约束；C4表示MEC处缓存的数据量不能超过其存储容量；C5和C6分别为MEC端整个计算资源和缓存资源约束。C7用于保证基站的SIC效率。

由于V2I通信的动态和随机特性，上述制定了基于V2I的计算卸载和缓存的随机优化模型。通过满足计算资源、缓存资源和任务缓冲区稳定性的所有约束，并考虑了车联网络环境的随机性和不可预测性来最小化与卸载缓存决策关联的平均能耗。综合了基于NOMA的车辆边缘计算网络的能耗和处理时延，利用李雅普诺夫优化算法将随机优化问题转化为动态规划问题，再通过解耦来进行求解。

2.2 问题转化

由于时间相关变量的存在，仍难以直接求解。此外，采用传统的启发式或迭代算法会带来较大的控制和延迟，这在高度动态的通信环境中是不可取的。因此，在本研究中利用李亚普诺夫优化理论来解决上述优化问题。

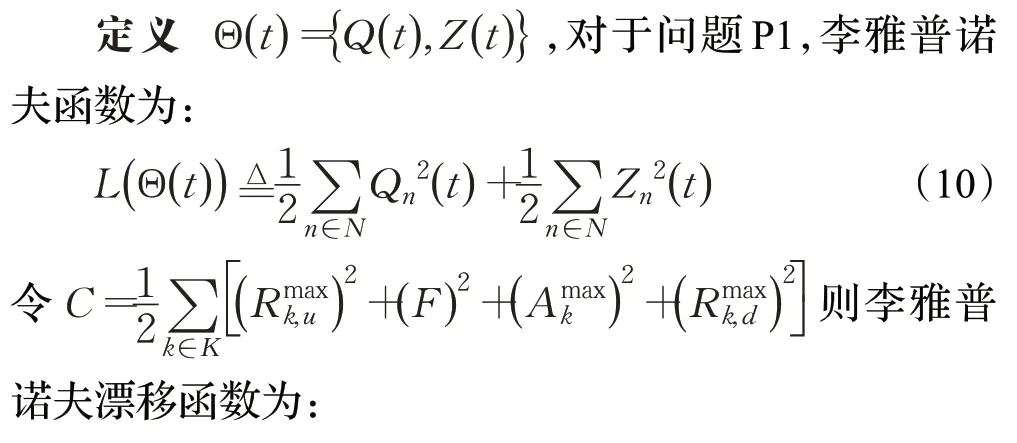
其中，V是非负控制参数用来权衡时延和能耗。基于随机优化理论，通过最小化公式（13）中漂移加惩罚函数上界，可以得到卸载、缓存决策以及计算和缓存资源分配。将时间相关问题P1转化为确定性问题P2，需要在每个时隙进行求解。问题P2为：

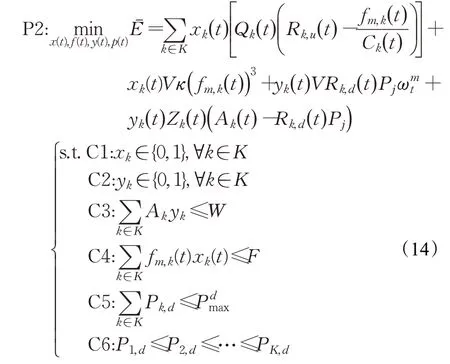
引理问题P2是一个混合整数非线性规划问题，存在NP-hard特性。

证明问题P2包括两大部分，一部分是卸载决策和计算资源分配，另一部分是缓存决策和缓存资源分配。为了更方便证明其NP-hard，假设已经确定了卸载决策和计算资源分配，将优化问题转化为负载分配问题，即需要寻找恰当的缓存和资源分配方法，以最小化系统能耗。假设每个车辆用户至少分配skbit大小缓存资源，负载分配问题又转为如何在缓存资源有限的情况下选择任务请求，使系统开销最小化问题，该问题属于0-1背包问题。而0-1背包问题属于NPC问题[16]，所以问题P2是NP-hard。其中系统总缓存资源代表背包的重量约束，每个任务请求车辆k是重量为sk的物品。

由此问题P2不易求解。以下过程将通过解耦为两个子问题进行解决。

3 联合优化卸载、缓存和资源分配

在以上问题P2中，涉及两组变量：（1）计算卸载部分中涉及的变量，包括xk(t)和fm,k(t)；（2）与内容缓存有关的变量，包括yk(t)和Pk,d(t)。两组的变量在目标函数和约束，因此P2可以解耦为计算卸载和内容缓存两个独立的子问题。具体地，在每个时隙t中，根据当前在队列Θ(t)的状态，执行算法。

3.1 计算卸载问题

问题P2的计算卸载子问题，包括卸载决策和计算资源分配问题，如下所示：

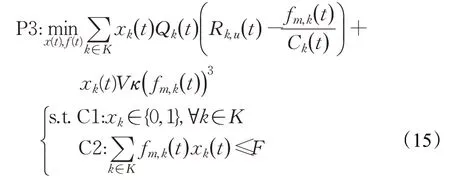
3.1.1 卸载决策

由于各移动车辆的卸载决策变量xk(t)是相互不影响的，因此可以解耦得到各移动车辆的卸载决策xk(t)。因此，xk(t)可以表示为：

3.1.2 计算资源分配

得到卸载决定后，P3可简化为确定进行计算卸载的移动车辆用户优化其计算资源分配。当xk(t)=1时。将用户集合表示为K1，并减少目标函数中的常数项，计算资源分配子问题如下：

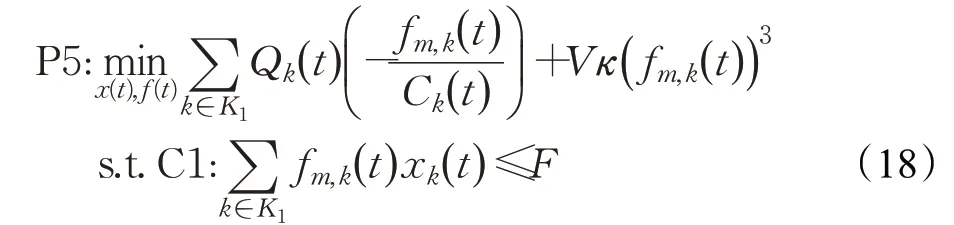
由于问题P5的目标函数是凸的以及限制条件是线性的，所以这是一个凸优化问题，采用内点法可以求出MEC端分配的最优CPU周期频率为：

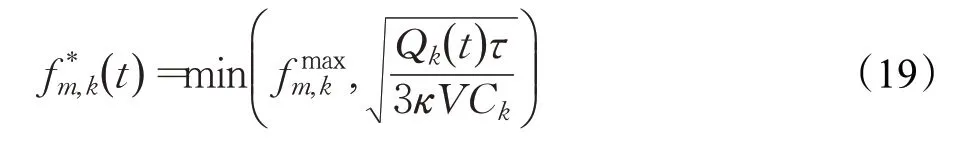
3.2 内容缓存问题

问题P2的内容缓存子问题，包括缓存决策和缓存资源分配：

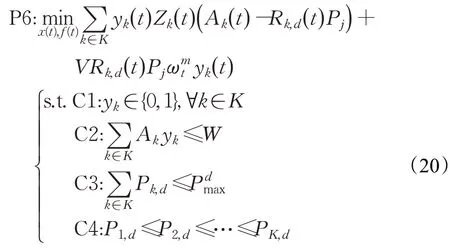
3.2.1 缓存决策

类似问题P3的求解过程，得出缓存决策。令Hk(t)=Zk(t)(Ak(t)-Rk,d(t)Pj)+VRk,d(t)Pjωm t，根据下式解出yk(t)：

3.2.2 缓存资源分配

将K2表示为缓存决策为1的车辆用户集合，则缓存资源分配问题为：

3.3 基于Lyapunov的联合优化卸载和缓存算法

为了更加清楚阐述卸载过程、缓存决策、计算和缓存资源分配，总结动态联合计算卸载，内容缓存，资源分配算法，给出了算法1。

算法1基于Lyapunov的联合优化卸载和缓存算法

4 仿真分析

在本章中，利用MATLAB仿真平台对所提出的基于NOMA的车辆边缘计算网络中的卸载和缓存资源优化方案进行验证。假设的仿真场景是在C-V2X标准规定下的车联网络系统中，通过Uu模式实现车辆终端和基站之间进行通信，文中参数按照移动边缘计算白皮书相关规定设置。设定仿真参数如表1所示。

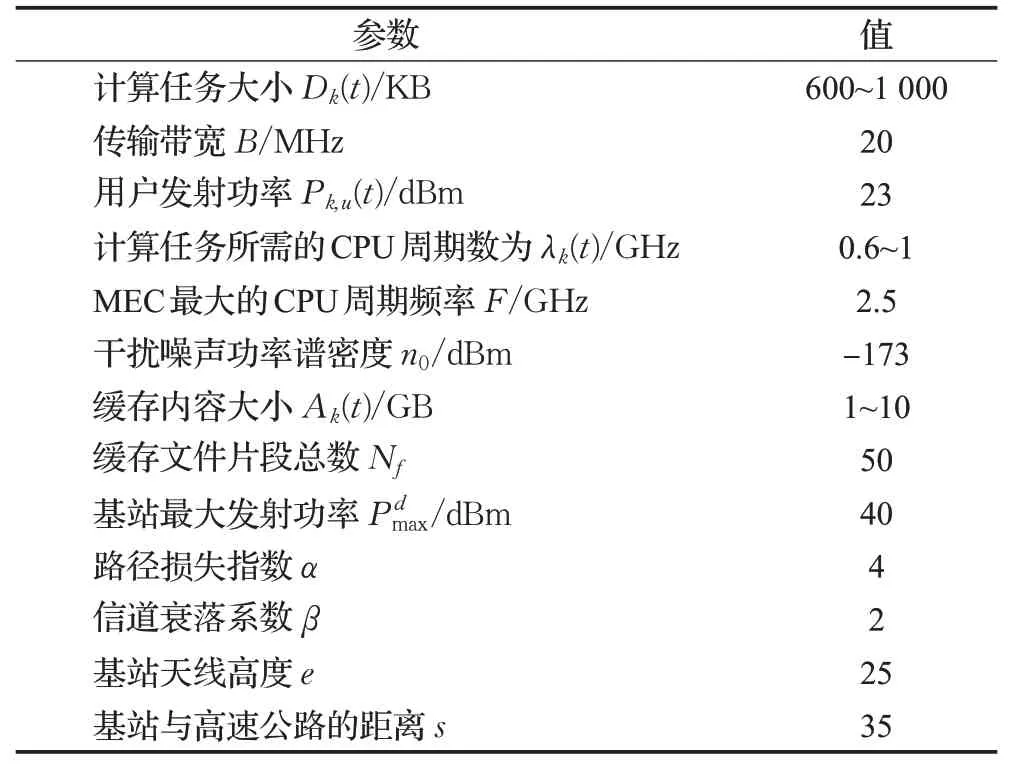
表1 模拟参数表Table 1 Analog parameter

将基于Lyapunov的联合优化卸载和缓存算法获得的性能增益与以下方案进行了比较：（1）无缓存。只优化与计算卸载相关的，不涉及内容缓存。（2）无卸载。只进行与内容缓存相关的优化，不优化计算卸载。（3）基于ADMM算法。根据与本文相同的卸载缓存场景文献[17]提出基于交替方向乘数法（alternating direction method of multipliers，ADMM）的优化算法。仿真过程中车辆用户的位置和衰落信道都是随机的。为了比较，采用正交多址（OMA）系统作为基准，其中K个车辆用户采用频分多址（frequency division multiple access，FDMA）方案进行通信卸载或者缓存。

图2和图3显示了不同移动车辆用户数量下的卸载能耗性能与控制参数的关系。可以明显看出在队列稳定性的条件下随着控制参数的增长，用户的队列总和随之增长，而平均能量消耗随之减少至趋于平稳。这表明基于Lyapunov的联合优化卸载和缓存算法在严格遵循长期时延约束的情况下，能够获得最优的能耗性能。同时在图2和图3中，也反映了车辆用户数量对卸载能耗和用户队列长度的影响。通过对比车辆用户数目为15和20时候的队列长度总和和平均能耗看出当车辆用户数量增加时，卸载和缓存能量消耗及队列长度总和都会增大。基于NOMA的方案在能量消耗以及时延方面优于OMA系统。这使得基于NOMA的卸载缓存方案对于需要执行大量用户任务的场景很有吸引力。

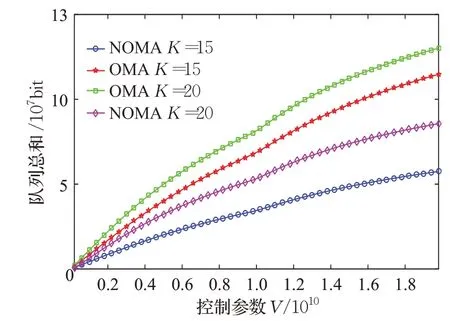
图2 控制参数对队列和长度的影响Fig.2 Impact of control parameters on queue

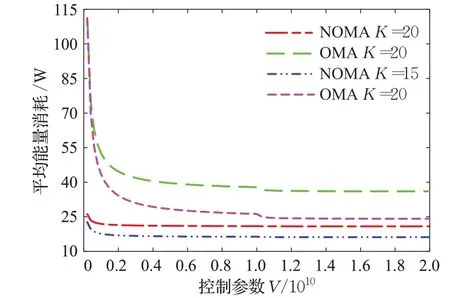
图3 控制参数对平均能量消耗的影响Fig.3 Impact of control parameters on average energy consumption

图4、图5分别展示了MEC服务器端的平均能量消耗与MEC的总计算资源(F)和缓存资源(P)之间的演化关系。图4中，MEC服务器端的平均能量消耗随着F的增加而减少，而无卸载的平均能量消耗保持不变，因为F对内容缓存没有影响。同样，可以从图5得出，MEC服务器端的平均能量消耗随着P的增加而减少，而无缓存的平均能量消耗保持不变，因为P对计算卸载没有影响。这种无卸载策略没有考虑任务数据是否卸载到MEC服务器以及无缓存策略没有考虑数据内容是否缓存到MEC服务器，导致较差的系统延迟和能量消耗。随着缓存资源的增加，可以在边缘服务器中缓存更多的数据内容。因此，更多的用户从边缘服务器获得响应，数据传输时间变得更短。然而，当资源达到一定的空闲值时，由于用户请求的数量是恒定的，因此总能耗降低至趋于平稳。结合NOMA并通过对计算卸载和内容缓存的联合优化，得出本文的算法性能总是最好的。

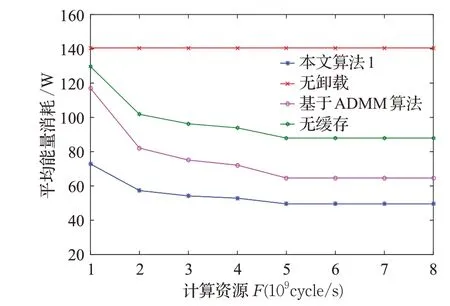
图4 计算资源对平均能量消耗的影响Fig.4 Impact of computing resources on average energy consumption

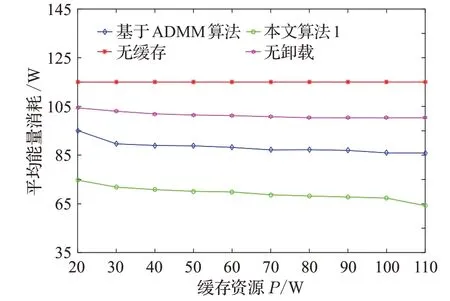
图5 缓存资源对平均能量能耗的影响Fig.5 Impact of cache resources on average energy consumption

5 结束语

本文利用NOMA技术对多车辆网络进行资源优化。通过联合优化计算卸载策略、计算资源分配、内容缓存策略和缓存资源分配，使得链路的平均能量消耗最小化。该问题已被表述为一个随机优化问题，并提出了基于李亚普诺夫优化理论的算法，便于分析易于处理。仿真结果表明，本文算法在最小化平均能量消耗方面具有良好的性能。