基于Widrow-Hoff算法的轧机单独传动系统同步控制

梁卫征，王延浩，李禹亭，张瑞成

（华北理工大学电气工程学院，河北 唐山 063210）

在轧机主传动系统中，单台电机拖动上下轧辊这一传动方式容易导致电机电流过大，使得轧制钢材时存在安全隐患［1］，需要考虑多台电机分别拖动上下轧辊这一传动方式，即轧机单独传动。因为上下电机的实际参数不同，使得输出转矩不同［2］，这将破坏产品质量。

近年来，诸多学者深入研究了如何拥有更好的同步性能。文献［3］通过逆变器将补偿信号和速度信号收集起来，最后输出控制信号来保持电机速度同步。文献［4］将模糊PID 算法与主从同步控制相结合，解决了速度不同步的问题。文献［5］提出了基于单神经元的PID 控制策略，辅以交叉耦合控制方法，有效地提高了两个电机的控制精度。文献［6］将模糊控制规则用于调整加权系数中，结合交叉耦合控制器，增强了系统的同步性能和抗干扰能力。

上述文献虽然从不同角度上实现了速度同步，但是同步的精度仍然存在不足，在受到干扰的情况下，不能及时恢复到速度同步。针对这一问题，提出了基于Widrow-Hoff 算法的交叉耦合同步控制策略，并同基于PI 交叉耦合同步控制器的系统以及基于PI 同步控制器的并行加补偿系统［7］进行对比。

1 直流电机数学模型

轧机单独传动系统中的电机模型可以表示为

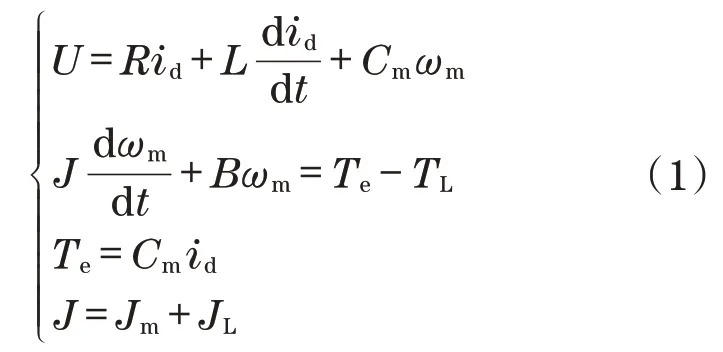
式中：U为输入电压；R、L分别为总电阻和总电感；id为电枢电流；Cm为转矩系数；ωm为角速度；Jm、JL分别为电机和轧辊的转动惯量；B为摩擦系数；Te为电磁转矩；TL为负载转矩。

图1给出了直流电机模型的结构图。

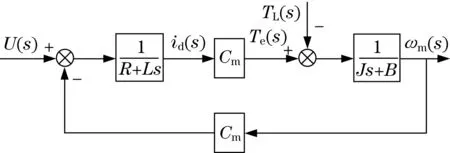
图1 直流电机模型结构Fig.1 Structure diagram of DC motor model

2 交叉耦合同步控制结构

图2 给出了基于交叉耦合的同步控制［8-9］结构。与主从同步控制结构［10-11］不同，交叉耦合同步控制结构中，任意一台电机受到扰动TL而导致的速度波动均可以影响其他电机，从而保持两台电机的速度同步。可见，该结构适用于高精度要求并且存在扰动的系统。

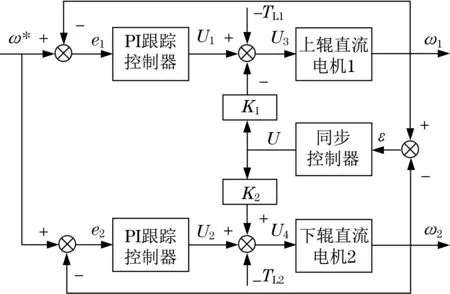
图2 交叉耦合同步控制结构Fig.2 Structure diagram of cross coupling synchronous control

3 神经网络同步控制器

作为近年来相当热门的控制算法之一，神经网络控制常被用于电机跟踪控制［12］、故障检测［13］和系统参数辨识［14］。

3.1 自适应线性神经元结构

自适应线性神经元网络［15］通过Wirdow-Hoff学习算法调整权值和阈值，不断减小均方误差，其结构如图3所示。

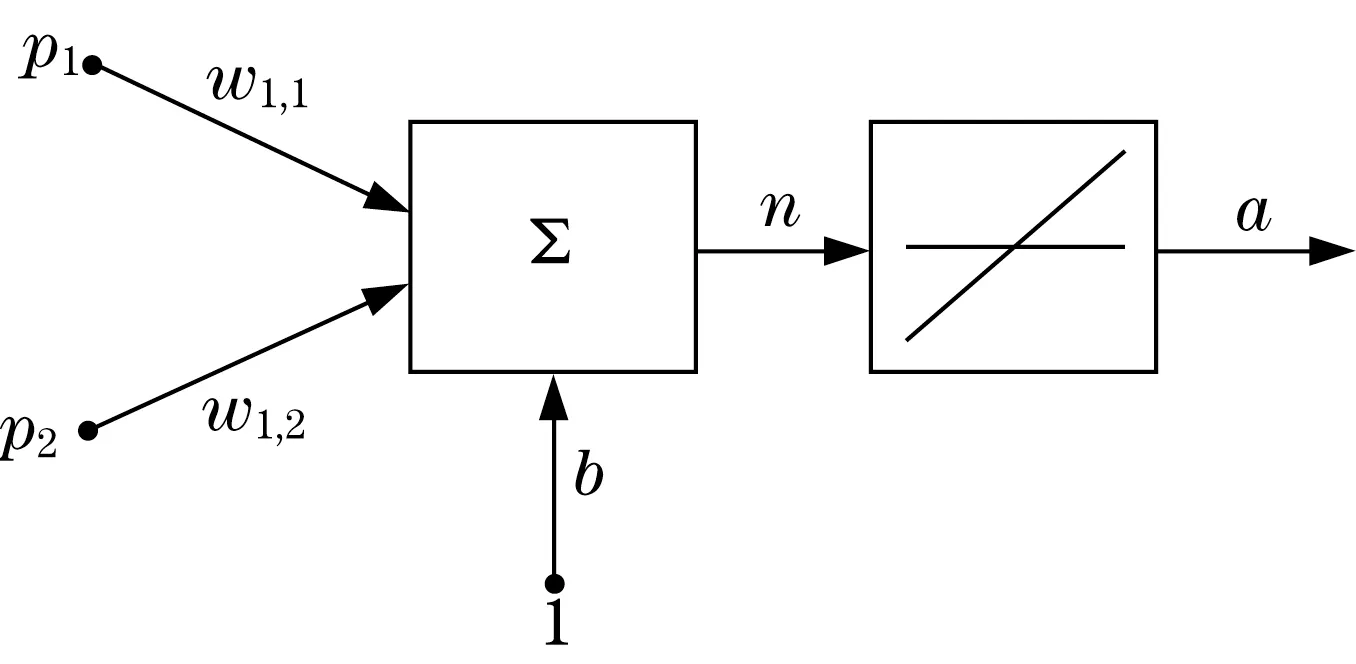
图3 双输入自适应线性神经元Fig.3 Dual input adaptive linear neuron

图3中，该神经元的输入为p1、p2，输出为

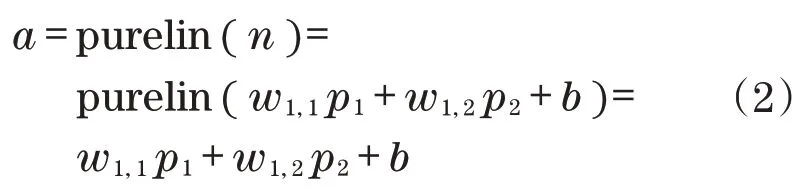
式中：w1，1、w1，2为权值；b为阈值；purelin(·)为激发函数。

3.2 神经网络同步控制器算法

令阈值b=0，线性激发函数purelin（·）为比例增益K，设p1、p2分别为k时刻和k-1 时刻的速度同步误差ε(k)和ε(k-1)，则输出u为

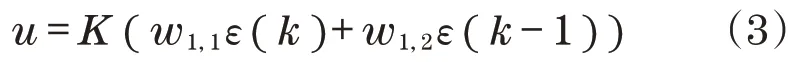
将E(k)代替k时刻的均方误差，得到性能指标为

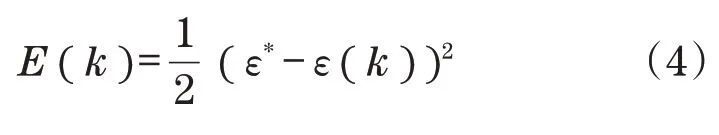
ε*为同步误差理想值，恒等于0。ε(k)为k时刻的速度同步误差为

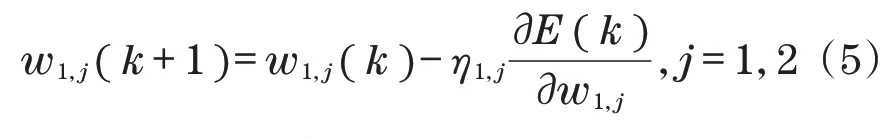
式中：η1，j为学习速率且大于0；w1，j(k)和w1，j(k+1)分别为k时刻和k+1时刻的权值；∂E(k)/∂w1，j为E(k)对w1，j的偏导数。

∂E(k)/∂w1，j的表达式为

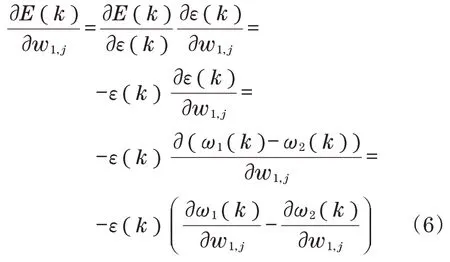
为 了 求 出∂E(k)/∂w1，j，需 要 分 别 求 出∂ω1(k)/∂w1，j和∂ω2(k)/∂w1，j。∂ω1(k)/∂w1，j和∂ω2(k)/∂w1，j的表达式分别为

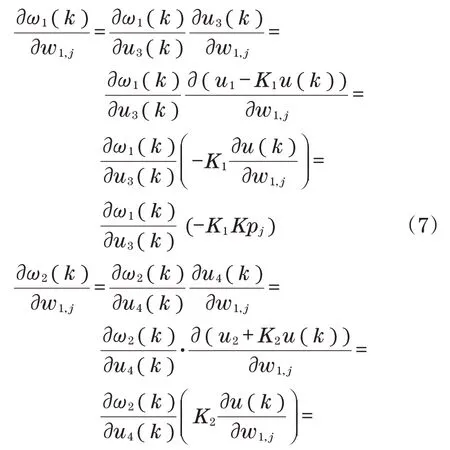
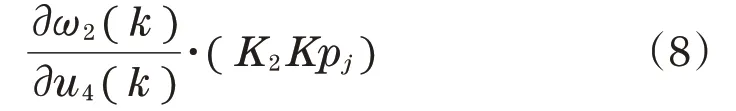
式中：pj(j=1，2)为同步控制器的第j个输入。

K1=K2=1，而2 个电机输出对输入的偏导∂ω1(k)/∂u3(k)、∂ω2(k)/∂u4(k)近似如下［16］：

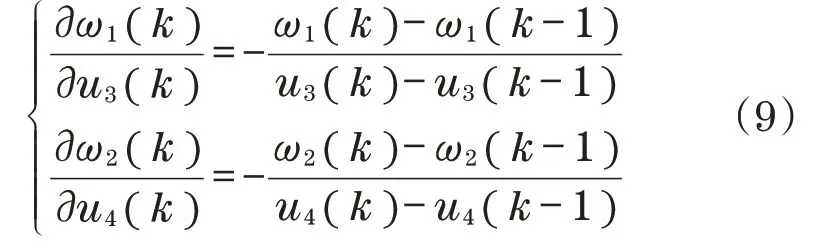
令p1=ε(k)，p2=ε(k-1)，综合上式，可以得出

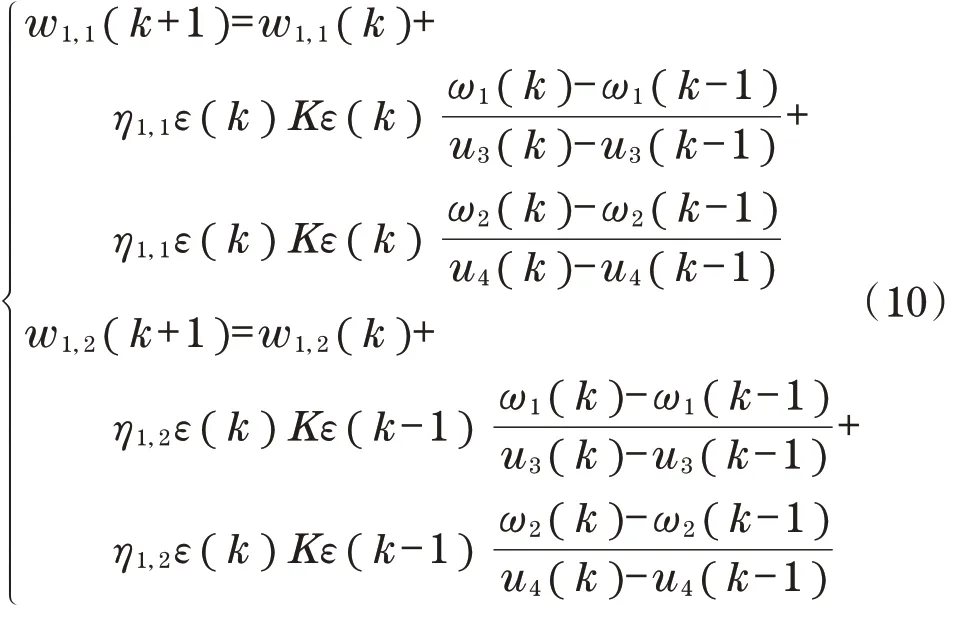
基于神经网络的同步控制器工作流程如图4所示。

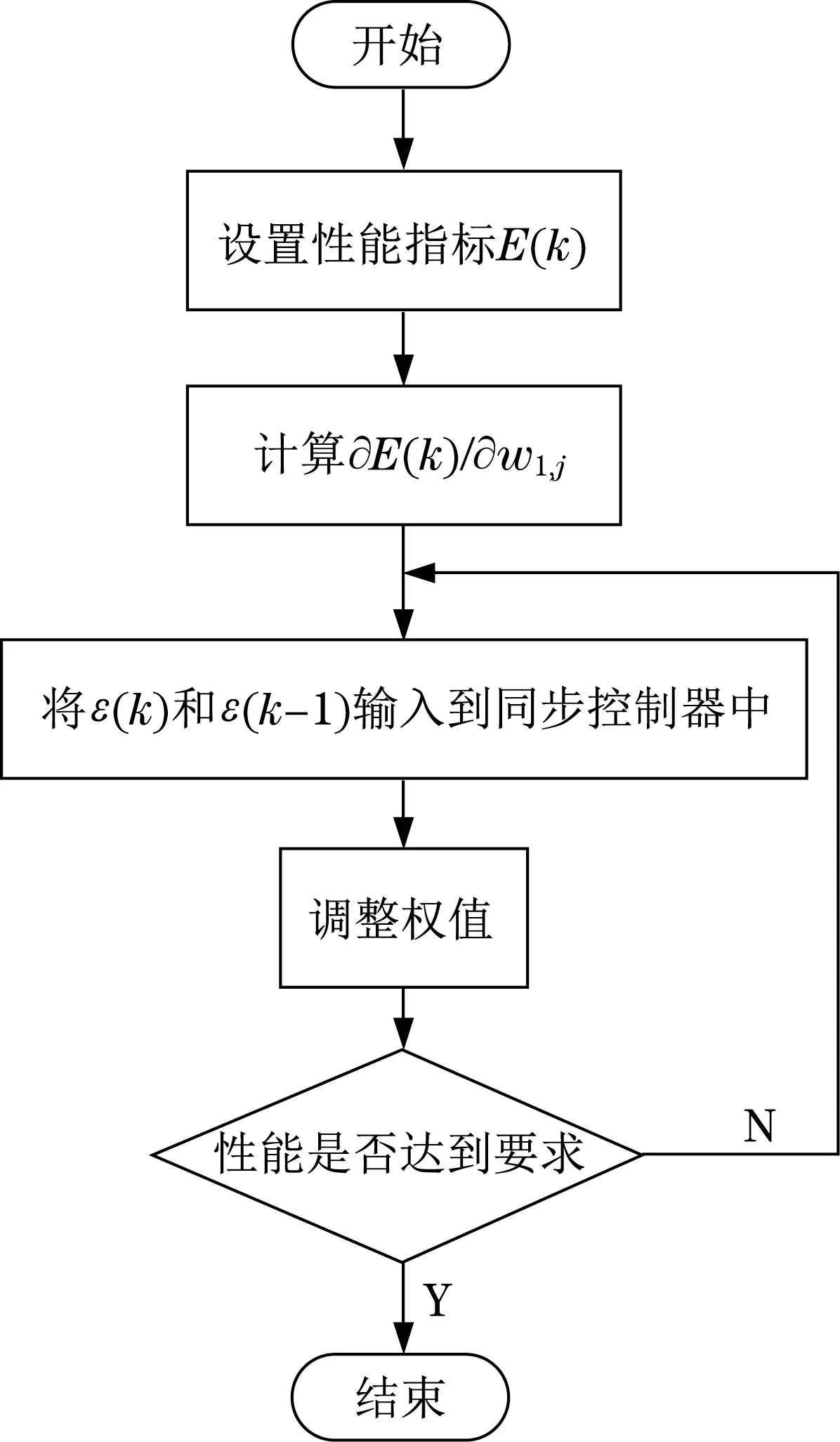
图4 神经网络同步控制器工作流程Fig.4 Work flow chart of neural network synchronization controller

4 实验仿真

4.1 实验参数

PI 跟踪控制器的参数为Kp1=20，Ki1=0.2，Kp2=24，Ki2=0.3；PI 同步控制器的参数为Kp=1.5，Ki=0.01。

神经网络同步控制器的权值初始值为w1，1=1.5，w1，2=0.01；学习速率为η1，1=0.6，η1，2=0.6；比例增益K=0.1。

表1给出了某厂上下辊的直流电机参数。

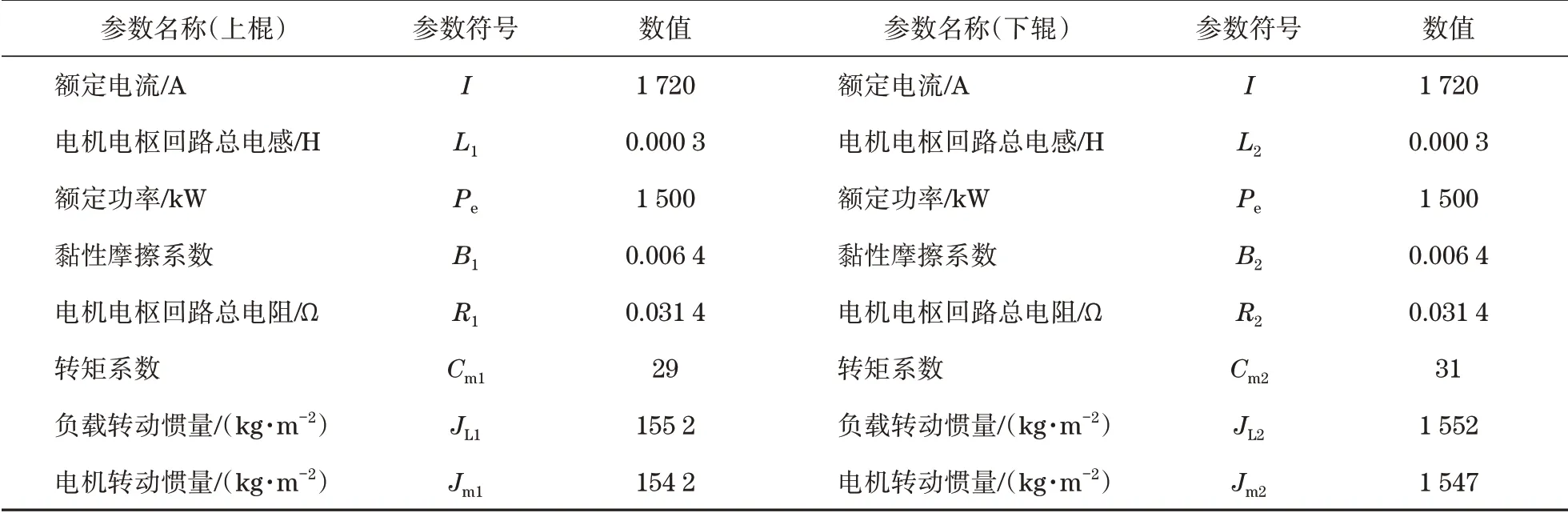
表1 直流电机参数Tab.1 DC motor parameters

2台直流电机的给定参考速度为ω*=23.7 rad/s。

4.2 实验结果

将上下轧辊直流电机作为实验背景，结合文献［7］设计出系统1。系统1 的结构为并行加补偿同步控制结构。针对系统1 进行改进，设计了系统2和系统3。系统2 和系统3 分别为基于PI 和基于Widrow-Hoff 学习算法的神经网络交叉耦合同步控制系统。用Matlab 软件进行仿真，3 个系统的仿真结果如图5和图6所示。

4.2.1 空载运行仿真

令电机空载运行10 s，仿真结果如图5 所示。由图5可得，上下辊电机在3个系统中达到稳定速度23.7 rad/s 所需时间如表2 所示。速度同步误差达到0.000 1 rad/s 所需的时间如表3 所示。在0.5～1.0 s内，与系统1、2相比，系统3的同步误差波动幅度最小，振荡次数最少。可见，与前2 个系统相比，系统3 的表现最好，所需时间最短。速度同步误差曲线振荡次数最少，恢复至稳定所需时间最短。

表2 3个系统上、下辊电机达到稳定所需时间Tab.2 Time required for the upper and lower roll motors of the three systems to reach stability

表3 3个系统同步误差达到0.000 1 rad/s所需时间Tab.3 Time required for synchronization error of three systems to reach 0.000 1 rad/s

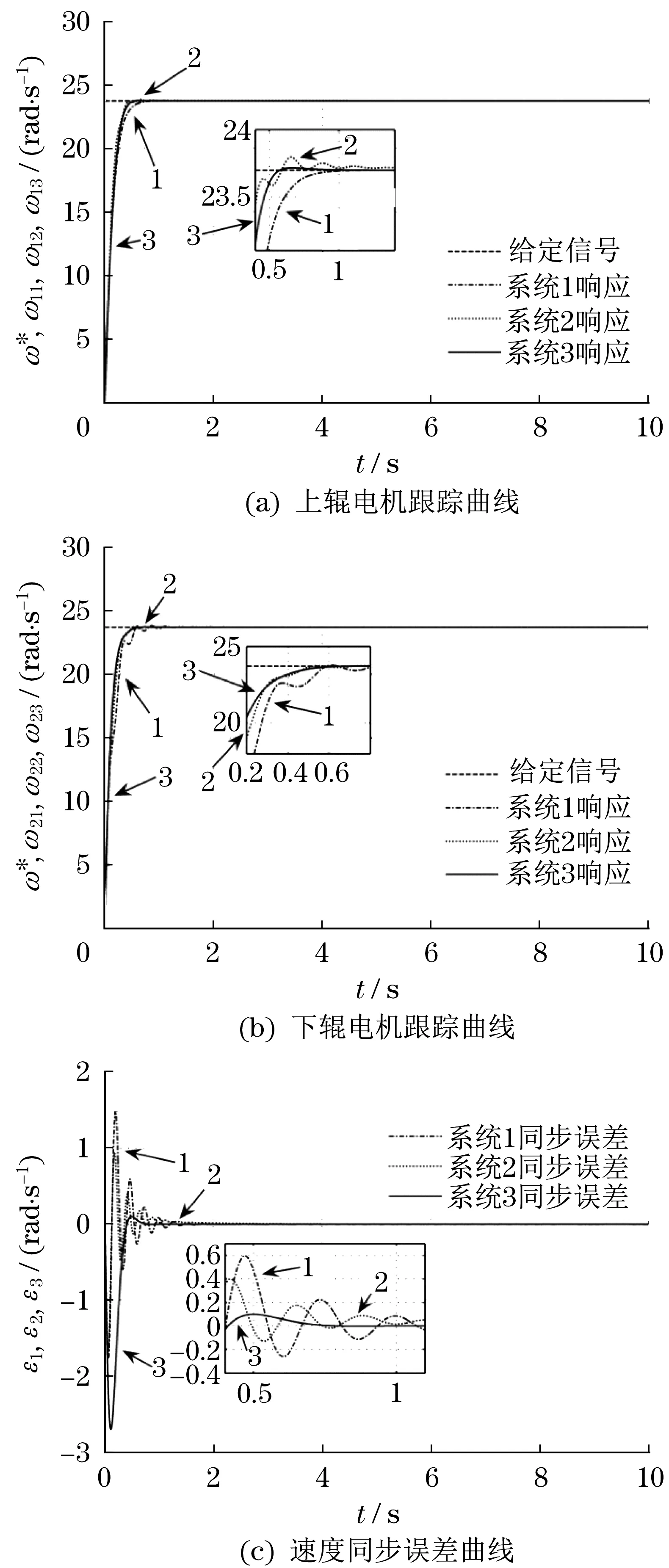
图5 空载运行仿真结果Fig.5 No load operation simulation results

4.2.2 轧机轧制钢材仿真

在第4 s 至第7 s，引入扰动TL1=TL2=14 500 N·m，仿真结果如图6所示。由图6可得，在加入扰动后，上下辊电机速度均会下降。上辊电机和下辊电机由速度开始下降直至恢复稳定所需时间如表4所示。扰动开始后，同步性变差。在4.2 s 时，系统3 的同步误差最大为0.06 rad/s。与系统1、2 相比，系统3的速度同步误差变化范围较大。而在4～5 s内，系统3 的振荡次数比系统1、2 的少。速度同步误差恢复至0.000 1 rad/s所需时间如表5所示。

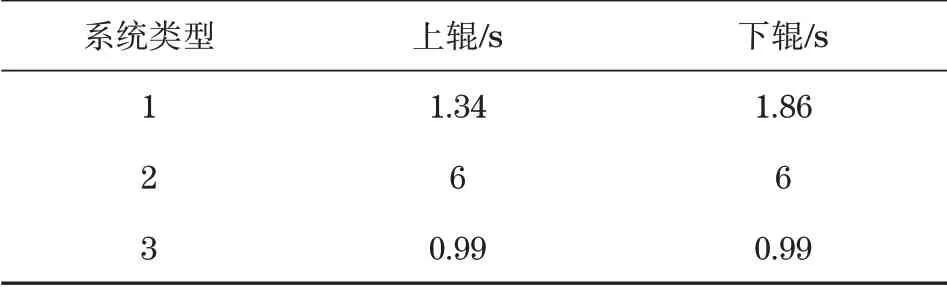
表4 3个系统上、下辊电机受扰后恢复至稳定所需时间Tab.4 Time required for the upper and lower roll motors of the three systems to recover to stability after being disturbed

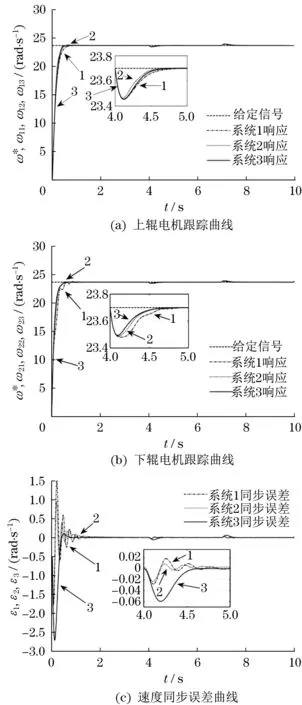
图6 轧制钢材仿真结果Fig.6 Simulation results of rolled steel

系统3采用神经网络同步控制器并用Widrow-Hoff 算法调整权值，在扰动加入时，由于设置的初始权值并不一定是最佳权值，且权值的调整需要时间，因此，在图5（c）中，系统3 的速度同步误差变化范围较大并出现较大的峰值。而在扰动消失时，由于权值需要重新调整，系统3 速度同步误差再次产生较大的波动。但结合表5 知，3 个系统中，系统3的速度同步误差恢复至0.000 1 rad/s 所需时间最短，同步性能最好。

系统1 和系统2 采用的是PI 同步控制器，它的参数是经过多次整定得到的，因此，在扰动加入后，系统1、2的速度同步误差变化范围要小于系统3的速度同步误差变化范围，而扰动消失时，由于PI 同步控制器参数不变，系统1、2 的速度同步误差变化范围依然小于系统3 的速度同步误差变化范围。但结合表5 知，系统1 的速度同步误差恢复至0.000 1 rad/s所需时间比系统2和系统3的长，其中系统2所需时间最长，在扰动下不能保持同步。

表5 3个系统同步误差恢复至0.000 1 rad/s所需时间Tab.5 Time required for three system synchronization errors to recover to 0.000 1 rad/s

由上数据和分析知，在加入扰动后，系统2 抗干扰性能比较差，在轧钢期间不能保持上下轧辊电机的速度同步，无法达到生产要求。而系统3 的恢复速度最快，抗干扰能力最强，且能保持速度同步。

5 结论

为了提高轧机上下辊电机速度的同步精度，提出了基于Widrow-Hoff 学习算法的神经网络交叉耦合同步控制系统，与PI 并行加补偿同步控制系统和PI 交叉耦合同步控制系统进行对比，通过分析仿真结果，可以得出以下结论：①上下轧辊空载时，新方法具有较高的同步精度，响应速度最快，同步时间最短，速度同步误差稳定在0.000 1 rad/s 以下；②上下轧辊轧制时，新方法的抗干扰能力最强，同步时间最短，并且在轧制期间，能保持速度同步误差在0.000 1 rad/s以下。