壁面粗糙性对两相驱替的影响规律

李大军，李晓燕，孙 海，张 磊，徐 超

1）中国石化胜利油田有限公司滨南采油厂，山东滨州 257439；2）中国石油长庆油田分公司油气工艺研究院，陕西西安 710018；3）低渗透油气田开发国家工程重点实验室，陕西西安 710018；4）中国石油大学（华东）石油工程学院，山东青岛 266580

非混相驱替在油气开发中具有重要的价值［1］．水驱是现在主要的开发方式，但在水驱油过程中产生的指进现象严重影响了开发效果，许多学者针对该现象做了很多研究．其中，KANG等［2］利用lattice Boltzmann（LB）多相多组分模型研究了两种不同黏度的非混相流体的流动，发现随着黏度比或毛细管数的增加，接触线的指宽和滑移距离均减小，而指长则增加．李维仲等［3］采用格子玻尔兹方法（lattice Boltzmann method，LBM）多组分模型模拟两相流体的驱替过程，研究水平通道内非混相驱替过程中的指进现象．结果表明，由于受重力作用的影响，指进前缘分布呈非对称形态分布；提高两相流体之间的黏度比，会增强指进现象的发生．刘佳威等［4］针对CO2泡沫相与原油体系，基于Shan-Chen伪势LBM模型，对多孔介质通道内CO2泡沫驱流动规律进行模拟，研究雷诺数、毛管数以及壁面润湿性对于非混相驱替过程中的黏性指进的影响．研究发现，雷诺数和毛管数的增大，会增强黏性指进现象，降低两相驱替效率．ANSARINASAB等［5］采用LBM的Cahn-Hilliard型自由能模型，建立该模型的等速边界条件，模拟非均质多孔介质中不同注入速率下驱替液的注入过程，验证了毛细管数、黏度比、润湿性和界面张力对非混相驱替的影响规律．

随着非常规油气的大力开发及研究人员对储层的进一步认识，近年来，很多学者认识到壁面粗糙度对于两相流体的影响不可忽略，裂缝壁面的几何形状对于两相流体驱替过程的影响不可忽略．部分学者研究了壁面粗糙度对于两相流体流动的影响规律．臧晨强等［6］采用改进的伪势LBM方法，研究复杂微通道内的两相驱替问题，结果表明，壁面的粗糙度对驱替过程也有重要影响，当向上凸起的半圆粗糙颗粒半径增加到一定长度时，壁面粗糙度的存在会降低驱替效率．张任良等［7］采用LBM和Shan-Chen多相流模型，研究微通道内几何结构和壁面润湿性对两相驱替的影响．研究结果表明，壁面的几何结构和润湿性对管流特性有一定影响，壁面的亲水性越强，驱替过程中受到的阻力越大，在粗糙颗粒间距变大时，流体越容易塌陷，使流体阻力增大．陈萍等［8］利用LBM模拟了在光滑和粗糙孔喉道中的水驱油的流动特性．研究发现，无论壁面的润湿性如何，壁面粗糙度始终是两相流动的阻力．由于粗糙度的存在，通道中会有一部分残余流体不能被驱替．WANG等［9］基于彩色流体LBM模型，定义量纲为1的粗糙度高度和粗糙度间距比来表征表面粗糙度．研究发现，与光滑通道中的非混相驱替相比，表面粗糙度的存在明显地推动了指进的形成．上述研究多集中在润湿性和毛管数方面影响，尽管体现出壁面粗糙度对两相流动的影响，然而对于壁面粗糙结构改变所产生的效果研究不够全面．

本研究采用相场模型与N-S方程进行耦合研究粗糙结构与黏度比改变对油水两相流动的影响，考虑一般矩形颗粒通道与复杂通道．同时对比不同黏度比在粗糙与光滑2种通道内产生的不同影响．

1 数学模型

1.1 研究方法

采用直接求解N-S方程的方法模拟两相流体在单一粗糙通道中的驱替过程，采用相场法实时追踪两相界面．

对于不可压缩流体，两相流体在通道中的连续性方程为

其中，u是速度矢量．

对于多孔介质中两相流体的动量方程其中，下标t表示对时间求导；t为流动时间；ρ为流体密度；p为流体压力；η为流体动力黏度；I为单位向量；Fst为界面张力．

1.2 两相界面追踪模型

在油水两相流动系统中，引入相场变量ϕ，相场变量设置为-1与1，分别对应水相和油相，在两相过度区域相场变量的值介于-1～1，表示相界面．界面区域混合自由能为

其中，E为混合能量密度．双势井函数f(ϕ)定义为

其中，ε为界面厚度．

通过将界面区域混合自由能对ϕ取变分，得化学势为

两相界面演化过程为

其中，γ为迁移率.

式（7）界面张力项可作为体积力项引入纳维-斯托克斯（Navier-Stokes，N-S）方程.

根据质量守恒方程，密度和黏度分别为

其中，ρ1和ρ2分别为2种流体的密度；η1和η2分别为2种流体的黏度.

设置边界条件为

其中，θw为被驱替流体的润湿角度；n为壁面的活向单位向量．

文献［10］曾使用一个毛细管渗吸的模型对上述相场模型进行了验证．

2 结果与讨论

2.1 壁面粗糙度对两相驱替的影响规律

壁面粗糙度的定量化表征是研究壁面粗糙度影响规律的关键．本研究采用文献［9］的表征方法．

相对粗糙高度的定义为

其中，h为粗糙单元高度；H为通道宽度.

粗糙单元间隙比用来表征水平方向的粗糙度，定义为

其中，l为粗糙单元的长度；L为两个粗糙单元的距离．

本研究通过设置不同的Hr和Sr模型，利用Comsol软件中的两相流相场模型进行模拟实验.设置初始参数为:采用尺寸为40μm×200μm的管道模拟油水两相驱替中壁面粗糙性对两相流动的影响．其中，粗糙通道中采用上下对称共26块粗糙颗粒，根据不同的Hr和Sr设置粗糙颗粒的大小．左端注入端压力为3 500 Pa，右端出口压力为0，通道上下壁面为无滑移边界条件．油和水的密度分别为ρo=890 kg/m3和ρw=1 000 kg/m3．为形成稳定的驱替过程，油相和水相黏度均为15 mPa·s．油水两相间的界面张力为σ=0.04 N/m，初始壁面为油湿75°．相界面长度定义为驱替相流体相界面顶端到最近三相接触点所在平面的垂直距离．不同时刻油水界面在光滑及粗糙喉道中的移动过程见图1．

图1 不同相对粗糙高度下两相驱替过程（t=0.001 s）Fig.1 Two-phasedisplacement at different relative roughness heights(t=0.001 s)

由图1可见，壁面粗糙度的存在会显著增大流动阻力，同时壁面粗糙度的存在将会有利于“润湿滞后”现象的发生，随着Hr的增大，润湿滞后现象更明显．其中，Hr越大，驱替过程中所受到的流动阻力越大．同时，壁面粗糙度的存在会降低接触线的滑移距离和相界面宽度，从而增强相界面的变形．这也是壁面粗糙度的存在会促进润湿滞后现象形成的主要原因．

图2对比了不同Hr下的相界面长度变化.由图2可见，当通道壁面光滑时，随着时间的延长相界面长度趋于稳定，且保持在一个较短的长度．而壁面粗糙度使得相界面长度持续增长，并且呈周期性变化，趋于形成黏性指进．导致这种现象的主要原因是壁面粗糙度的存在，会降低接触线的滑移距离从而抑制三相接触点的移动．同时较大的Hr会在相界面变形的过程中“打断”相界面，从而使得三相接触点“瞬移”到下一个粗糙单元上，导致相界面长度突然减小，并且相界面被“打断”的次数与长度变化的周期数相同，这种现象随着Hr的增大而变强，这是较高Hr的通道中，相界面不能发育的更长的主要原因．

图2 不同H r的相界面长度随时间的变化Fig.2 Phase interface length as function of time with different H r

图3为不同的Sr的通道内界面顶端的移动距离.由图3可见，Sr越小，流动阻力越小，故流动速度越大．同时粗糙度的存在也会降低驱替效率，增大驱替过程完成的时间．

图3 不同S r的相界面顶端长度随时间的变化Fig.3 The top length of the phase interface as function of timewith different S r

2.2 黏度比对两相驱替的影响规律

黏度比（M）对于两相驱替的影响主要是形成黏性指进，黏度比越大，指进长度越长.本研究中，分别模拟M=1、4和10，研究黏度比对于两相驱替影响，粗糙颗粒为2μm×2μm，其余参数与2.1节中设置相同．

图4为整个驱替过程中相界面长度的具体变化情况.光滑通道的指进长度先增大后稳定在一个较短的长度；而粗糙通道中，相界面长度由于受到粗糙单元的影响，将会周期性的变化，总体的界面长度也大于光滑通道．造成这种现象的原因是壁面粗糙度抑制接触线的滑移，从而增加相界面的长度．每当三相接触点走过一个粗糙单元，接触线将会受到粗糙颗粒的影响而被“打断”，从而使相界面重新分布．

图4 M=1时界面长度随时间变化Fig.4 Thecurvesof interfacelength asfunction of time with M=1 for smooth wall and rough wall

图5为驱替过程中相界面顶端的移动距离，能反应出在通道中的驱替速度大小.由图5可见，壁面粗糙度的存在将会显著增大两相流动阻力，降低驱替速度，同时驱替过程中速度大小基本保持恒定．

图5 M=1时相界面顶端移动距离随时间变化曲线Fig.5 Themoving distancesof thetop of thephase interface as function of time with M=1 for smooth wall and rough wall

图6和图7分别是驱替过程中两相界面长度变化和相界面顶端长度变化情况.由图6和图7可见，当M=4时，无论是在光滑通道还是粗糙通道中，相界面长度都逐渐增加，这与M=1时的恒定相界面长度有所不同．在光滑通道中，M=4时的最大指进长度大于M=1时，粗糙通道中，相界面长度的变化周期随着黏度比的增大而变长，同时当M＞1时，相界面长度会周期性变长．造成上述结果的原因是黏度比增大导致两相流动过程中黏滞阻力的增大，故驱替速度降低．同时黏度比的增大导致驱替过程中形成黏性指进，黏性指进与粗糙度的双重影响将会增大界面长度，抑制接触点的滑移，这也是导致界面长度变化周期增长的原因．

图6 驱替过程中两相界面长度变化曲线图(M=4)Fig.6 The length change curves of two-phase interface during displacement(M=4)

图7 驱替过程中相界面顶端长度变化(M=4)Fig.7 The top length of the phase interface changes(M=4)

进一步增大M取值，当M=10，由图8和图9可见，两相流动阻力，驱替速度将会进一步增大，同时在驱替过程中，相界面长度也随着时间的延长而增加，但是相比于M=1和M=4，粗糙通道中相界面长度的变化周期会增长，相界面的发育时间增加，同时由于黏度比的增大，驱替将不会通过整个通道，这也是图中相界面长度小于M=4的原因．黏度比对于两相驱替的影响是形成黏性指进，随着黏度比的增大，黏性指进现象越明显．在粗糙通道中，黏度比的增大会使相界面的发育周期增长，使得相界面长度呈周期性增加．

图8 驱替过程中两相界面长度变化曲线图(M=4)Fig.8 The curves of length change of two-phase interface during displacement(M=4)

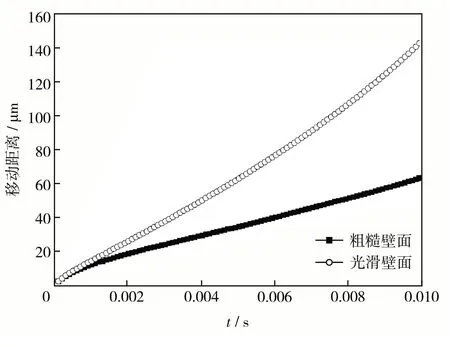
图9 驱替过程中相界面顶端长度变化(M=4)Fig.9 Thetop length of thephaseinterfacechangesduring displacement(M=4)

2.3 复杂结构对两相驱替的影响规律

设M=4，注入压力p=4 KPa，其余条件与2.1节中相同，模拟研究复杂粗糙表面与光滑表面对于两相驱替的影响规律．并将模拟结果与简单模型所得一般结论进行对比分析，验证结论的正确性．模拟结果如图10．

图10 复杂粗糙通道和光滑通道驱替过程Fig.10 Displacement processof complex rough channel and smooth channel

由图10可见，在相同时间内，不论是两相界面顶端还是接触线的移动距离，均大于粗糙壁面通道，初步分析是壁面粗糙度的存在增大了两相流动阻力．同时，真实的复杂模型相界面分布并不规则，是一种非对称的形式，这是由于上下壁面的粗糙度不同，所以对于接触线和三相接触点的抑制情况也有所不同，故接触点的位置不同，造成了界面分布不规则的现象．另外，这也是出现润湿滞后现象的原因．

图11和图12分别对比了光滑壁面和粗糙壁面驱替过程中的相界面长度（其中三相接触点的选取以最近的三相接触点为准）变化以及相界面顶端移动距离的变化过程．由图11可见，在驱替刚开始时，光滑通道界面长度的增长速度是大于粗糙壁面的，这是由于驱替刚开始时，粗糙壁面流动阻力大，故相界面顶端增长速度缓慢，而接触线并未发生滑移，所以相界面长度变化较慢．而当光滑通道内接触线发生滑移时，粗糙通道并没有发生这种现象，故在之后粗糙通道内的相界面长度持续增长的原因．这与前面所得结论一致．同时，由于受到壁面粗糙单元的影响，粗糙壁面内的相界面长度并非持续增长，而是整体上呈增加趋势，局部上并不总是增加的.受到壁面粗糙度的影响，反而表现出局部“振荡”的变化，与粗糙单元的分布和粗糙程度大小有关，与简单规则模型取得的结论有一定的差别．由图12可见，壁面粗糙度对于相界面长度的影响很大，不可轻易忽略．图12的曲线斜率代表驱替速度大小，壁面粗糙度的存在会增大两相流动阻力，降低驱替完成的时间，同时由于粗糙度的存在，将会有一定的剩余油未被驱出，降低了两相驱替效率．

图11 驱替过程中相界面长度的变化Fig.11 Variation of phase interface length during displacement

图12 驱替过程中相界面顶端长度变化Fig.12 Changes of the top length of the phase interface during displacement

3 结 论

利用Comsol软件研究壁面粗糙度的存在对于两相驱替的影响规律，采用相对粗糙高度Hr和粗糙单元间隙比Sr表征粗糙度，研究黏度比M对于两相驱替的影响规律，又通过设计复杂模型，模拟验证简单模型所得出的一般性规律．

1）与光滑表面通道相比，粗糙壁面会增大两相流动阻力，降低驱替速度，并出现润湿滞后现象．同时，在粗糙单元间会有部分剩余油未被驱出，降低两相驱替效率．

2）壁面粗糙度的存在会促进两相界面的变形，抑制接触线的滑移，从而增加相界面长度．同时，壁面粗糙颗粒的存在也会在与相界面发生接触时“打断”相界面，从而缩短相界面的长度，使得相界面长度发生周期性变化．

3）当被驱替流体润湿壁面时，有利于相界面长度的发育，而当驱替流体润湿壁面时，相界面发育受到抑制．在M=1时，无论是光滑壁面还是粗糙壁面，均可以形成相对稳定的相界面；当M＞1时，在光滑壁面通道中，相界面长度会随时间延长而增加，而在粗糙通道中界面长度呈周期性增加，同时相界面变化周期增长．

4）对于复杂模型通道中，由于粗糙单元分布不均匀，使得相界面呈非对称形式分布，同时在复杂粗糙通道中，相界面的总体变化趋势以及对两相驱替的影响规律与简单模型相同，但是局部的变化并不一致．