基于Pareto最优解的跨流域调水泵站多目标优化运行研究

朱博文，龚 懿*，陈再扬，王诗文，陈永丰

（1.扬州大学 水利科学与工程学院，江苏 扬州225000；2.溧阳市水利局，江苏 溧阳213300）

0 引 言

【研究意义】南水北调工程是解决我国水资源空间分布不均的重要工程措施。其中，东线工程受地形影响建有大量低扬程、大流量跨流域调水泵站。该类跨流域调水泵站具有安装机组多、单机流量大、运行时间长、提水费用大的特点。由于其年运行时间长，在保证提水目标实现、机组运行寿命等基本要求的基础上，如何更好地兼顾运行过程中的经济性和安全性，实现泵站多目标优化运行，具有十分重要的意义。

【研究进展】目前，国内外对泵站（群）优化运行已有许多研究，在模型构建方面主要是以泵站运行费用最小[1-4]、耗电量最低[5-7]或各机组总体效率最高[8]为目标，在模型求解方面主要包括动态规划法[9]、遗传算法[10]、蚁群算法[11]、狼群算法[12]、人工蜂群算法[13]等。程吉林等[14]考虑峰谷电价及潮汐影响，以耗电费用最少为目标，构建叶片可调单机组优化数学模型并利用动态规划求解，结果表明，在潮型不变的情况下变角优化运行方案较常规运行方案有更好的经济性。龚懿等[15]以泵站站内多机组日运行耗电费用最低为目标，构建泵站站内多机组叶片全调节优化运行数学模型，利用大系统分解-动态规划聚合法求解，获得较好的优化结果。张倩[16]基于城市污水泵站的特点，构建包含泵站出流流量时段间变幅最小目标、泵站能耗最小目标、机组启停次数最小目标的污水泵站优化运行数学模型，利用分层序列法化简后采用遗传算法求解。梁兴等[17]以调度周期内机组启动次数衡量维修成本，建立以抽水电费最小及机组启动次数最少的多目标优化数学模型，并基于Pareto 最优解理论采用混合粒子群算法求解，结果表明片面追求泵站经济运行可能会导致机组启停机次数增加引起维修成本急剧增加。孔波等[18]以调水量最大、发电量最大和能耗最小为目标构建电站-水库-泵站群多目标优化数学模型，通过改进布谷鸟算法获得Pareto 解集，结果表明该模型各项指标合理，具有一定的优势。

【切入点】以往研究表明，在泵站优化运行过程中水泵机组需要频繁调角、变速、开停机。由此导致机组间提水流量差异较大，易在泵站出水池形成较大的回流区或折冲水流，产生比较严重的壁面冲刷[19-20]。对于大型跨流域调水泵站，运行时间长、单机组流量大，机组间出水管流量差异程度对泵站安全运行影响尤为明显，而到目前为止大多数研究并未考虑优化运行后出水水流对泵站出水池的冲刷，由此带来的不安全因素随着运行时间的增加缓慢累积，最终可能造成严重的后果。

【拟解决的关键问题】本文在泵站单机组单目标变角优化、站内多机组单目标变角优化研究的基础上，探索考虑经济和安全运行的泵站多目标优化运行的复杂非线性数学模型构建及其系统工程求解方法，分析不同工况下站内多机组优化运行方案，确定最佳运行组合，研究成果对跨流域调水泵站经济、安全运行具有较强的理论及现实意义。

1 考虑经济安全的泵站多机组多目标优化模型构建

以一个调水周期内泵站运行提水耗电费用最小，以及一个调水周期内各时段泵机组间出水流量不均匀度最小为目标，以各时段各机组叶片安放角为决策变量，以提水期内泵站提水总量、电机配套功率、各机组启停机次数为约束条件，构建以下泵站多机组多目标优化运行数学模型。

1.1 目标函数

1）运行费用最小目标：

式中：f1为泵站1 次调水期内运行最小耗电费用（元）；Z1为泵站1 次调水期内运行耗电费用（元）；M为水泵机组台数；j为机组编号，j=1、2、3、…、M；N为1 次调水期内划分的时段数；i为时段编号，i=1、2、3、…、N；Qi，j(θi，j)为第i时段第j台水泵流量（m3/s），在扬程、转速一定时，为叶片安放角θi的函数；Hi为第i时段的时均扬程（m）；Ti为第i时段的时段长度（h）；Pi为第i时段的峰谷电价（元/（kW·h））；ηi，j（θi，j）为第i时段第j台水泵的装置效率（%），与第i时段流量、扬程有关；γj为第j台水泵的电动机效率，在负荷大于60%时，可以认为基本不变，按94%考虑；σj为第j台水泵的传动效率，按直联机组考虑，取100%。

2）各时段各机组流量不均匀度最小目标：

式中：f2为泵站1 次调水周期内各时段各机组流量不均匀度最小值（m3/s）；Z2为泵站1 次调水周期内各时段各机组流量不均匀度大小（m3/s）；为第i时段各机组的平均流量（m3/s）。在本文中各时段各机组流量不均匀度定义为：各机组提水流量与该时段机组平均流量差值的绝对值总和与机组台数的比值。

1.2 约束条件

目标提水量约束：

电机配套功率约束：

开停机次数约束：

式中：W为泵站目标提水总量（m3）；Ni，j（θi，j）为第i阶段第j台水泵机组对应于叶片安放角θi.j的实际功率（kW），应小于等于第j台水泵的电动机配套功率N0，j；Dj为第j台水泵运行期内间断性停机次数，考虑到大型水泵频繁开停机过程对泵机组损耗较大，应小于各台机组规定的间断性停机次数Dj，0。

2 模型求解

2.1 模型特点及求解思路

上述模型为多约束多目标非线性数学模型，目标一为泵站1 次调水期内运行费用最低；目标二为泵站1 次调水期内各机组间流量不均匀度总和最小。一般地，可以将原模型通过一定方式变换为单目标问题的标量化方法来求解（权重法）。但多数情况下，由于各目标之间物理意义及数量级之间差异，通过权重法将多目标问题转换为单目标问题进行求解，效果并不是很理想。

对于本文而言，2 目标函数间存在的相互关系使得最优解不一定唯一，通常可以求得不比任何解差的解集，该解集可以称之为Pareto 最优解。

2.2 求解方法

1）多目标遗传算法求解Pareto 前沿

为了解决泵站多目标优化运行问题，本文使用基于Pareto 最优解的多目标遗传算法对模型进行求解，主要是以基本遗传算法的选择、交叉、变异为基础，引入Pareto 最优解概念解决多目标优化问题[21-22]。

在多目标优化问题中，根据解的优越关系定义Pareto 最优解。对于本文，即任意的2 个决策向量X1=（θ1，1，θ1，2，…，θN，M）、X2=（θ’1，1，θ’1，2，…，θ’N，M）若满足：

式中：fsuit为目标函数值对应的适应度大小；s、k为目标函数序号；X1、X2为任意2 个泵站各机组各时段叶片安放角决策向量。

则可以称X1支配X2，在解空间内如果不存在解X支配X1。X1即为非支配解，这样的解的集合就是非支配解集或称为Pareto 前沿。

快速非支配排序多目标遗传算法（NSGA-II）是在非支配排序遗传算法（NSGA）的基础上引入拥挤度和拥挤度比较算子，克服了NSGA 算法需要人工指定共享半径的适应度共享策略的弊端，使得Pareto 前沿分布更加均匀，多样性更好[23]。

某个体的拥挤度是指在经过归一化处理后的Pareto 前沿中，包含该个体但不包含任何其他个体的最大矩形的长短边之和的大小。除第1 个及最后一个个体，其余个体的拥挤度可以表示为：

式中：dp为种群中第p个个体的拥挤度大小；s为目标函数序号。

在运算过程中，各台机组各时段的叶片安放角θi，j为决策变量，每个决策向量X中共有M×N个决策变量，每个决策向量即为多目标遗传算法中的一个个体。快速非支配排序及拥挤度计算主要包括以下步骤：

①计算每个个体不同目标的适应度大小并保存。

②通过比较每个个体不同目标的适应度数值大小，获得每个个体被支配的数量。

③将种群中的个体通过被支配数量升序排列。

④将升序排列的种群中首末2 个体拥挤度d 设为无穷大，从第2 个个体开始拥挤度按式（7）计算。

⑤将种群中个体以被支配数大小再次进行升序排列，同时比较拥挤度大小，若被支配数相等则拥挤度大的个体排序在前。

2）确定泵站多机组最佳运行方案

对于某一特定问题通常需要寻求一个确定的解。为此，需要进一步构建评价函数对求得的Pareto 前沿中的解进行评价。考虑到构建的多目标模型的目标物理含义不同，数量级相差也比较大，本文采用对Pareto前沿中的各组非劣解的目标函数值进行归一化后，与理想点距离远近作为评价指标，选取距离理想点最近的一组非劣解作为最佳运行方案[24]。这里的理想点是指Pareto 前沿中同时取得目标函数最小值的点，在归一化后即为坐标轴原点，距离是指在平面迪卡尔坐标系中两点间空间相隔大小。求解步骤如下：

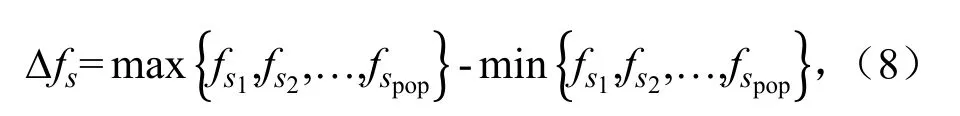
式中：Δfs为Pareto 前沿中，第s个目标的最大值与最小值之差。

式中：ms为Pareto 前沿中，第s个目标的最小值。

式中：f为归一化后，Pareto 前沿中各点距离理想点的大小。

将Pareto 前沿中的每组解代入式（8）—式（10），当f取得最小值时，其所对应的各时段机组叶片安放角即为最佳运行方案。

3）机组最佳运行方案的修正

根据《泵站技术管理规程（GB/T 30948—2014）》中的推荐，在泵站的实际运行过程中，在满足供排水计划的前提下，可以通过站内机组运行调度和工况调节，改善进出水池流态，减少水力冲刷和水力损失。在前文所述过程中，已经获得了一个提水周期内各时段各机组叶片安放角的最佳运行方案，在不改变目标函数值的基础上还可对同一时段内各机组的运行状态进行修正，以期最大程度上达到减小水力冲刷的目标。

为减少水力冲刷，根据水流的特性，水利工程一般采用对称布置的形式[25]。对于提水泵站而言，在满足计划提水量的要求下，尽可能使同一提水流量的机组沿泵站中轴线对称布置，是一种管理成本低且行之有效的方法。一般地，在同一时段内，机组叶片安放角度的不同是导致站内机组间流量差异的最大因素。故在实际运行过程中，叶片安放角相同的机组应当尽可能地对称布置。据此，可对已得到的机组最佳运行方案进行修正。

3 实例求解与分析

3.1 江都4 站基本情况

江都4 站位于江苏省扬州市，是南水北调东线工程源头泵站之一，安装7 台套同型号立式轴流泵，水泵叶片为液压可调式，叶轮直径为2 900 mm，设计叶片安放角0°，调节范围[-4°，+4°]。水泵额定转速150 r/min，电动机额定功率3 440 kW。考虑到优化计算工作量，在优化求解时取离散步长为2°。考虑到提水周期长度影响，单机组日运行过程中停机次数上限取2。

江都4 站不同年型（丰水、平水、枯水）、不同月份可能发生的日均扬程变幅为3.8～7.8 m；长江扬州段为感潮河段，不同年型、不同月份的潮型基本保持不变，日均潮差在1.1～1.3 m，变幅不大。在模型实际分析中，对潮型进行了概化，各种工况的潮差均以1.2 m 计[26]。以日均扬程7.8 m 为例，日均扬程变化过程如图1 所示。

根据江苏省发展改革委公布的江苏电网2020—2022年的峰谷分时销售电价[27]，从00:00 开始，全天共划分5 个时段，峰谷分时段电价如图2 所示。

图2 峰谷电价分时段价位Fig.2 Peak-valley price time-sharing price chart

图1日均扬程7.8 m 概化潮位过程Fig.1 Generalized tidal level process with daily average head of 7.8 m

考虑到大型水泵不宜频繁开停机及受长江潮位变化引起的泵站扬程变化，考虑以1日为提水周期，从17:00 时开始划分为9 个时段，每个时段的泵站时均扬程及分时电价与其组合关系如表1 所示。

表1 各时段电价及对应时均扬程（以日均扬程7.8 m 为例）Table 1 Electricity price and corresponding time-average head for each period(taking daily average head 7.8 m for example)

3.2 单工况下优化结果与分析

将本文构建的多目标优化模型应用于江都4 站日运行优化，采用基于Pareto 最优解的多目标遗传算法（NSGA-II）进行求解。日均扬程为7.8 m，100%提水负荷目标提水量大于等于2.065×107m3时[28]，其Pareto 前沿如图3 所示。

从图3 可以看出，在解空间范围内，Pareto 解分布均匀，在部分区间呈现阶梯状下降趋势。由于日提水总量约束的要求，Pareto 前沿并非连续分布。当不均匀度最小时，泵站优化运行费用最高为38.16 万元，当费用最小时流量不均匀度达到19.47 m3/s。在Pareto前沿中，理想解应为同时取得流量不均匀度最小及运行费用最小的点，但显然二者无法同时取得。将Pareto前沿中的各组解归一化后，理想解为（0，0），与其距离最近的点为（0.393 9，0.531 1），如图4（a）所示。对应的运行费用f1=37.46万元，不均匀度f2=7.67 m3/s。所以选定（f1=37.46 万元，f2=7.67 m3/s）（即图4（b）中最优解）对应的各时段机组运行状态（表2 所示）为各时段机组最佳运行状态。在最佳运行状态下，相较于Pareto 前沿中费用最小点（f1=36.66 万元，f2=19.47 m3/s）费用增加0.8 万元，机组间流量不均匀度减小11.8 m3/s 与不均匀度最小点（f1=38.16 万元，f2=0）相比费用减少0.7 万元，机组间不均匀度则增加7.67 m3/s。在与Pareto前沿中费用最小点的对比中，费用上升2.2%，流量不均匀度下降达到60.6%。

图3日均扬程7.8 m、100%负荷时Pareto 前沿Fig.3 Pareto front at daily head 7.8 m and 100%load

图4 Pareto 前沿分布Fig.4 Pareto front distribution

表2日均扬程7.8 m、100%提水负荷各时段机组最佳运行状态Table 2 Average daily head 7.8 m，100%water lifting load optimal operation state of units in each period

由于江都4 站7 台机组为同一型号立式轴流泵，假定各机组性能特性无显著差异，故在相同时段，同一运行状态的机组提水流量相同。考虑到相同提水流量的机组对称布置有利于出水侧水流平顺，不易产生较大的回流或冲刷，故还需对各时段机组运行状态进一步修正。在全天9 个时段中，时段1 及时段9 存在机组间流量不相等的情况。将站内七台机组按照顺序编为1～7 号，时段1 的第4 台机组停机，其余机组以-4°的叶片安放角度开机运行；时段9 的第4 台机组以0°的叶片安放角度开机运行，其余机组以-2°的叶片安放角度开机运行。各时段各机组优化运行状态如表3，各时段各机组分配流量如图5 所示。

从图5 可以看出，除时段1 及时段9，其余各时段各机组流量相同，时段1 机组4 流量为0 m3/s，其余机组流量为28.78 m3/s。时段9 机组4 流量为32.94 m3/s，其余机组流量均为30.41 m3/s，机组4 相较于其他机组流量增大8.31%，表明该时段各机组间流量均匀度良好。

各时段提水量及该时段对应电价如图6 所示，在低电价时提水量相应增加，高电价时提水量相对较少，与经验相符合，表明优化结果可以满足费用最小的目标。

图6 各时段提水量与电价对照Fig.6 Comparison chart of water yield and electricity price for each period

表3日均扬程7.8 m，提水目标2.065×107 m3 时江都4 站运行方案Table 3 Average daily head 7.8 m，water extraction target 2.065×107 m3 No.4 Jiangdu pumping station operation scheme

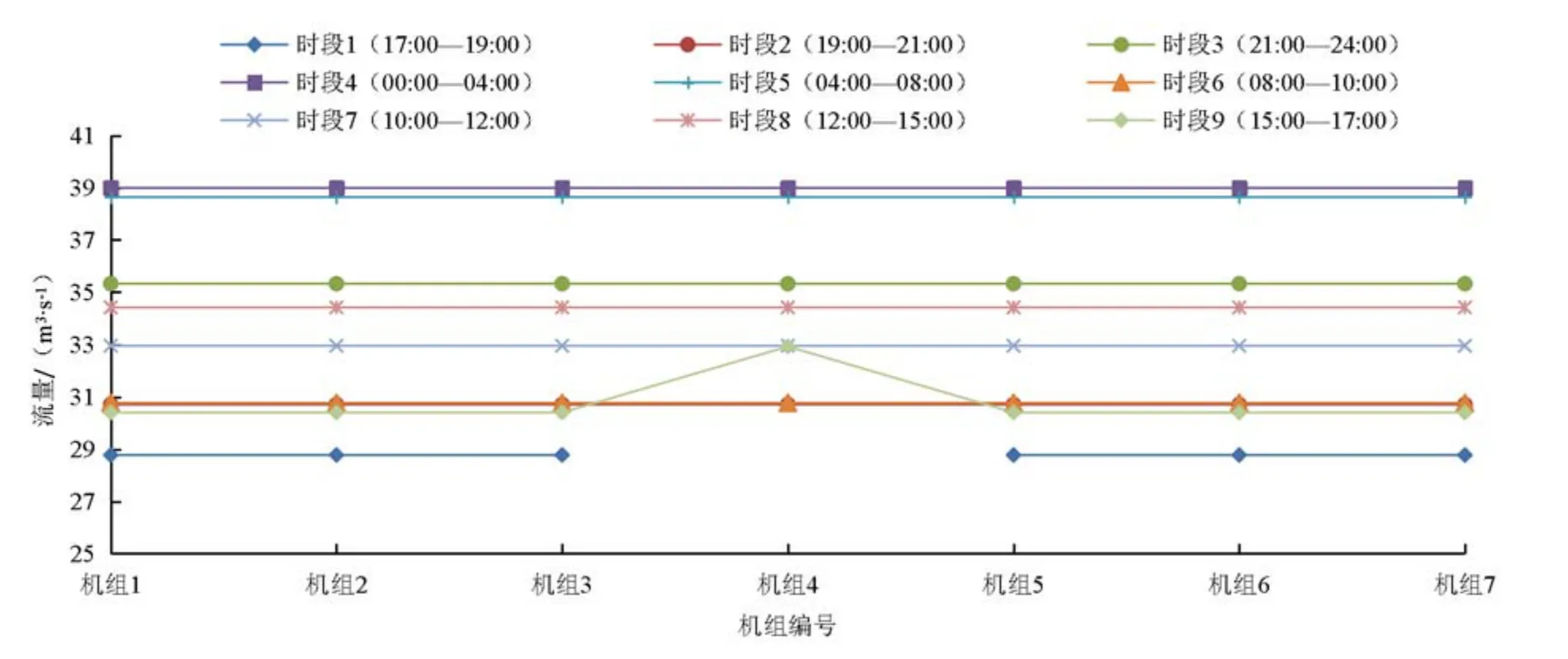
图5日均扬程7.8 m，100%负荷江都4 站各时段各机组流量分配Fig.5 Daily average head 7.8 m，100%load No.4 Jiangdu pmping station each period of each unit flow distribution

3.3 不同工况条件下的优化结果与分析

采用上述方法，可得到不同日均扬程H（3.8～7.8 m）、不同提水负荷（100%、80%、60%）情况下江都4 站站内多机组优化运行单位提水费用（图7）和机组间流量不均匀度（图8）。

图7 不同工况日优化运行单位提水费用Fig.7 Optimal operating unit water extraction costs for different working days

图8 不同工况日优化运行机组不均匀度Fig.8 Unevenness of optimized operation units in different working conditions

从图7 可以看出，当扬程在3.8、4.8 m 时，由于机组停机次数约束的存在，不同负荷下单位提水费用差距较小，但总体均随扬程的增加而增加。在同一扬程不同提水负荷下由于存在机组间流量不均匀度最小这一目标及停机时段数的约束情况较为复杂。以日均扬程3.8 m、100%负荷为例，每万m3提水费用为94.79 元，80%及60%负荷下每万m3提水费用分别为96.62 元和98.32 元，呈负荷越大单位提水费用越小的规律。由图8 可知，对于机组间流量不均匀度这一目标函数，在不同提水负荷下总体呈随扬程的增大而减小的规律，不均匀度在7.05～11.6 m3/s 围内，均匀度相对较好。在100%负荷下，由于目标提水量较大，各时段各机组会趋向于全部开机运行，导致该时段的各机组间流量不均匀度显著增加，造成该扬程条件下全时段流量不均匀度较大，故在100%负荷下机组间流量不均匀度呈较大波动。

各日均扬程及不同提水负荷下江都4 站优化运行较常规运行单位提水费用节约幅度如图9 所示。可以看出，日均扬程7.8、6.8、5.8、4.8 m 和3.8 m 时不同提水负荷下优化运行较常规运行单位提水费用分别节约1.55%～18.57%、3.78%～16.74%、6.29%～15.83%、5.54%～15.00%、1.31%～15.60%。相较于常规运行的各机组全部额定叶片安放角运行而言，虽然流量不均匀度有增加但是单位提水费用下降明显，具有比较好的经济效益。

图9 各运行工况下优化运行与常规运行单位提水费用节约幅度Fig.9 Saving range of unit water extraction cost under optimal and conventional operation conditions

各日均扬程及不同提水负荷下江都4 站优化运行不均匀度较Pareto 前沿中费用最小点对应流量不均匀度下降百分比如图10 所示。由图10 可知，各工况下流量不均匀度相对于Pareto 解集中费用最小点对应的机组运行方案下降比较明显，最高在100%提水负荷下日均扬程4.8 m 时流量不均匀度下降76.04%，最低在60%提水负荷下日均扬程6.8 m 时流量不均匀度下降17.46%。按照Pareto 前沿表现出的规律，随着费用的下降，流量不均匀度将上升，若仅考虑费用最小目标对泵站优化运行，则相对于Pareto前沿中费用最小所对应的运行方案，其流量不均匀度更大，与之相比本文所定最佳运行方案的流量不均匀度下降幅度将超过现有数据。因此，具有十分优良的安全性。

图10 不同工况下机组流量不均匀度下降幅度Fig.10 The decline range of unit flow non-uniformity under different working conditions

4 讨论

从Pareto 前沿的分布中可以清晰地发现泵站各机组间流量不均匀度与运行费用之间存在显著相关，随着流量不均匀度的增加泵站运行费用逐渐减小。本文提出的多目标优化模型相较于文献[1-4]以单一的运行费用最小为目标而言，在满足提水量需求的前提下可以有效兼顾泵站运行的安全性，更有利于泵站的长期安全运行。同时，由于同一时段各台机组运行趋向于一致，也可以大大减少运行管理的负担，减少运行中出现错误的概率。此外，相较于文献[17]中将泵站群运行费用最低及机组启动次数最小作为目标，本文提出的模型更注重于单座泵站的长期安全运行，对于泵站群的优化运行也可在本文提出的模型基础上对水量或扬程优化分配。

以江都4 站为研究实例，通过选取最优解得到的最佳运行方案，单位提水费用较常规运行方案在100%、80%和60%提水负荷下平均节约12.44%、14.26%和3.69%，流量不均匀度较Pareto 前沿中费用最小点对应的运行方案在100%、80%和60%提水负荷下平均分别下降64.82%、58.12%和56.27%，效果显著，可为泵站管理决策部门借鉴与参考。

本文考虑泵站运行过程中的经济性及安全性，将泵站运行费用最低及机组间流量不均匀度最小作为目标，但在泵站实际运行过程中机组的启停次数等也会对泵站运行的安全性造成很大的影响，文中仅将一个提水周期内单台机组的停机次数设置为约束条件，未来可以在泵站运行费用及机组间流量不均匀程度为目标之外，同时考虑机组的启停机次数对泵站运行安全性的影响，使得模型在兼顾安全性能方面更加全面、合理。

5 结论

将本文构建的模型运用于江都4 站，结果表明，对于拥有多台机组的跨流域调水泵站，随着泵站优化运行费用的最小值的减小，机组间的流量不均匀度最小值呈上升趋势。

将模型确定的最佳运行方案与Pareto 前沿中费用最小方案对比，流量不均匀度下降达到60.6%，但运行费用仅上升2.2%，表明模型确定的最佳运行方案在运行费用上升不大的情况下可以更好地兼顾泵站运行的安全性。

对于不同服役年数的泵站，依据泵站运行管理的相关规定可以构建不同的评价模型对Pareto 前沿中的个体进行评价，选择适合于具体泵站的运行方案。