基于指定性能的非线性系统数据驱动滑模控制
杨祎桀, 刘 冬, 曲袁超
(1. 沈阳航空航天大学 自动化学院, 沈阳 110136; 2. 辽宁大学 数学与统计学院, 沈阳 110136)
0 引 言
随着科学技术的快速发展,实际受控系统的复杂性日益增加,使得系统建模愈加困难。在此背景下,系统在线数据的利用显得格外重要。数据驱动控制方法在控制器设计过程中只使用输入输出数据,而不需要系统的精确数学模型,从而引起了研究人员的广泛兴趣。近年来,出现了许多数据驱动控制方法,如无模型自适应控制[1]、虚拟参考反馈整定[2]和迭代学习控制[3]等。
现代控制理论与方法可以很好地解决机理模型可精确获取和机理模型可获取但含有不确定因素2种被控对象。但对于复杂的高阶、强非线性的被控对象,机理模型很难建立或不可获取。因此,无模型自适应控制方法由于不需要数学模型的显式或隐式知识而引起了广泛关注。无模型自适应控制方法首先在文献[4]中被提出,在文献[5-7]中被扩展和完善。基于动态线性化技术和伪偏导数的概念,研究人员沿闭环系统的动态操作点建立了一系列的局部动态线性化数据模型,包括紧格式动态线性化、偏格式动态线性化和全格式动态线性化等效的局部动态线性化数据模型。迄今为止,无模型自适应控制已成功应用于许多领域,如无人驾驶技术等[8]。
另一方面,滑模控制方法因其对不确定性和外界干扰的鲁棒性以及具有较快的收敛速度而得到广泛应用。为了充分利用无模型自适应控制和滑模控制的优点,文献[9]中引入了一种基于无模型自适应控制的离散滑模控制器。随后,在文献[9]的启发下,出现了各种类型的无模型自适应滑模控制器。在文献[10]中,针对不确定机器人系统模型不准确和参数时变的问题,提出了一种无模型自适应滑模控制方法,证明了即使在无法建立准确模型的情况下,所提出的方法也可使不确定机器人系统稳定。滑模控制中的抖颤问题不可避免地影响着控制性能,为此,研究人员提出了许多抑制抖颤问题的方法,如趋近律法和边界层法等。
为了实现静态和瞬态条件下的跟踪性能, 同时保证变换误差系统的稳定性, 在文献[11]中提出了指定性能控制方法。 近年来,许多文献将指定性能控制方法与其他方法相结合并应用于各种系统中。 如文献[12]在考虑指定性能和全状态约束的基础上提出了一种事件触发自适应控制算法, 解决了一类非严反馈非线性多智能体系统的一致性跟踪问题。 针对一类带有输入死区约束的严反馈非线性系统, 文献[13]将指定性能控制与模糊控制、最优控制、backstepping方法及命令滤波技术和自适应动态规划技术相结合, 设计了一种最优反馈控制器。
基于上述讨论,针对单输入单输出离散非线性系统,本文提出了一种基于指定性能的无模型自适应滑模控制方法。与已有的具有预先定义性能的滑模控制器设计文献相比,本文引入一种新的正切型误差转换函数,以保证跟踪误差收敛到预定义的可调边界内,不同于现有的常用误差转换函数[14]。 除此之外,将一种新的滑模控制框架与指定性能方法相结合,并通过构造符号之间的关系,证明了系统的稳定性和收敛性。 与现有的指定性能方案[15-17]相比,该设计方法仅依赖于被控对象的输入输出测量数据,在提高工业信息利用率的同时,消除了建模所带来的困扰。
1 问题描述
1.1 非线性系统的动态线性化
考虑下列离散时间非线性系统:
y(k+1)=f(u(k),…,u(k-nu),y(k),…,y(k-ny))
(1)
其中:函数f(·) 代表未知的非线性函数;u(k)和y(k)分别为系统在k时刻的输入和输出;nu和ny为它们相应的阶数。
假设1 函数f(·)关于系统输入u(k),u(k-1),…,u(k-nu)的偏导数连续。
假设2 非线性系统(1)满足广义利普希茨条件。即对于任意时刻k,若||φ(k)||≠0,则有|Δy(k+1)|≤χ||φ(k)||成立。其中φ(k)=[Δy(k);Δu(k)],Δy(k)=y(k)-y(k-1), Δu(k)=u(k)-u(k-1),χ为一个大于零的常数。
从实际角度来看,假设1描述了常见非线性系统的一般条件,假设2表示系统输出变化率是受系统输入变化率限制的,因而上述2个假设具有合理性。基于以上2个假设,引入一个被称为伪偏导数的时变向量ψ(k)=[ψ(1,k);ψ(2,k)],使得系统(1)被描述为
y(k+1)=y(k)+φT(k)ψ(k)
(2)
考虑以下代价函数:

(3)
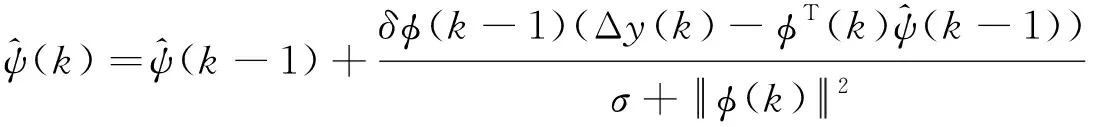
(4)
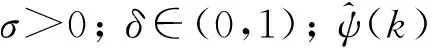
1.2 指定性能函数
考虑以下的离散时间正递减边界和光滑函数ρ(k):
追踪误差定义为e(k)=yd(k)-y(k),yd(k)为预期轨迹,α和β为2个正数,代表着追踪误差的边界范围可调。边界初值ρ(0)>边界终值ρ(∞)>0,γ∈(0,1)为收敛率。显然,光滑函数ρ(k)是收敛的。
指定性能控制保证了追踪误差维持在预定义的边界(5)内。在严格单调递增函数Ω(ε(k))中引入变换误差ε(k),使得
e(k)=ρ(k)Ω(ε(k))
(8)
其中递增函数Ω(ε(k))对于任意ε(k)∈R有以下性质:
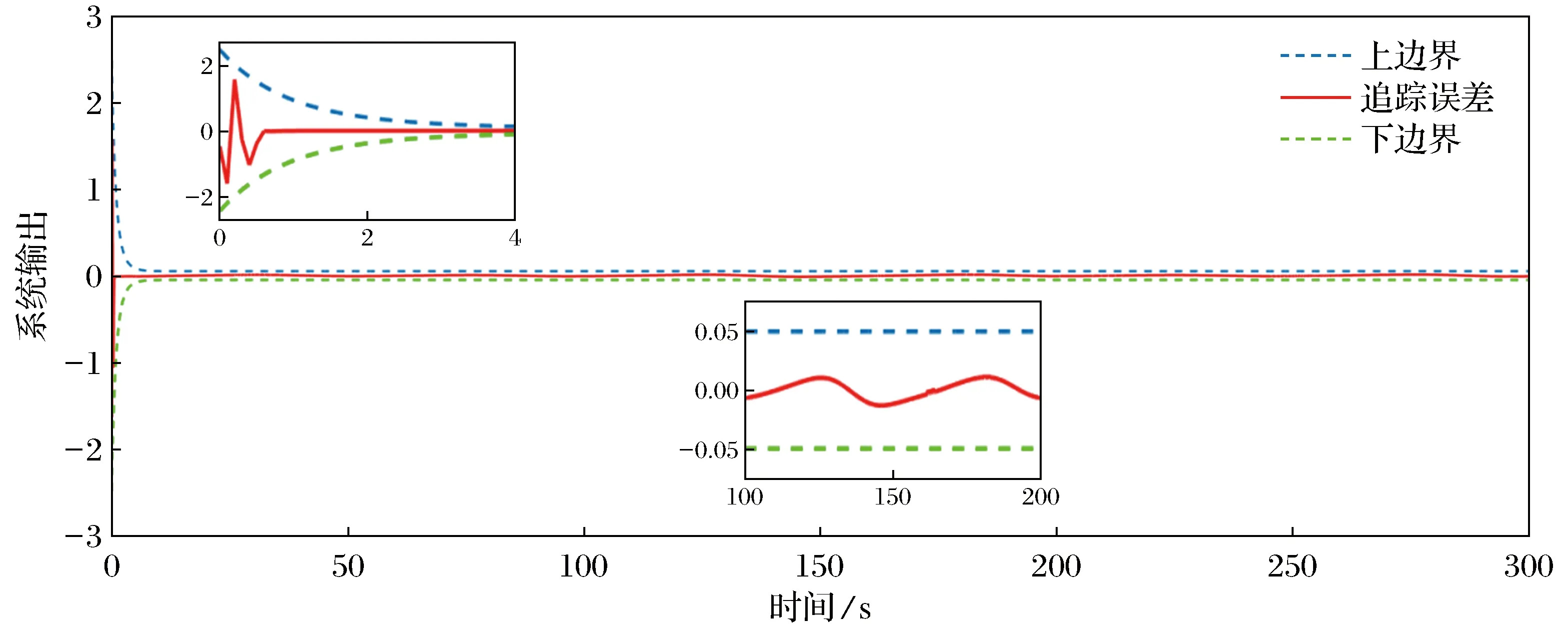
选择合适的参数初值使得-ρ(0) (9) 因此,ε(k)可以表示为 (10) 当α≠β时,2个可调收敛边界的参数函数α(k),β(k)调整如下: 其中α(0)和β(0)为α(k)和β(k)的初值,满足如下条件: 修改后的收敛域和变换误差函数重新定义为 在接下来的控制器设计中将会使用修改后的约束条件。另外,约束条件(13)和max{·}函数的存在保证了任意时刻下的Ω(ε(k))∈(-1,1)。 此外,参数ρ(0),ρ(∞)和γ是影响控制性能的关键因素。参数ρ(0)表示初始阶段误差的基本最大约束值,参数ρ(∞)决定稳态跟踪误差的最大允许边界,参数γ为可调约束边界的收敛速度。 不同于一般的滑模面,本节对于离散时间非线性系统(1),在如下的滑模面构造中考虑变换误差ε(k),而不是传统的追踪误差e(k)。 s(k)=s(k-1)+κε(k)-ε(k-1) (15) 其中1<κ<2。在变换误差式的作用下,式(15)可以进一步表示为 (16) (17) 在趋近律Δs(k+1)=s(k+1)-s(k)的作用下,结合式(16)和式(17),可以推导出如下的等效控制律: (18) u(k)=u(k-1)+ue(k)+us(k) (19) 给出开关控制律us(k)如下: (20) (21) 为方便起见,定义以下函数: (22) 联立式(16)、式(17)、式(21)和式(22),滑动函数可以更新为 (23) 引理1[18]由正切函数的(2,2)阶帕德近似可得以下关系: 定理1 在任意时刻k,θ(k)与ε(k)符号相同,与ε(k+1)符号相反。 再联立式(17)、式(21)和式(22)可得 (24) (25) 从引理2可以得到 (26) 通过已知的符号关系不难看出ε(k)tan(θ(k))+κ>0恒成立。 将式(25)的两边同除以θ(k),再由引理2可推导出以下恒不等式: (27) 对于该不等式,假设θ(k)>0,可知ε(k)/(ε(k)tan(θ(k))+κ)>ε(k+1)。 1) 若ε(k)>0,由于ε(k)tan(θ(k))+κ>0,可以推导出ε(k+1)/ε(k)小于1/(ε(k)tan(θ(k))+κ)的最小值为0。也就是说,此时ε(k)与ε(k+1)符号相反。 2) 若ε(k)<0,同理可以推导出ε(k+1)/ε(k)大于1/(ε(k)tan(θ(k))+κ)的最大值为+∞,此时显然产生了矛盾。 综上所述,在θ(k)>0的假设下可知ε(k)>0且ε(k+1)<0。那么在θ(k)<0时,同理可知ε(k)<0且ε(k+1)>0。由此证明了θ(k)与ε(k)符号相同且与ε(k+1)符号相反的结论。 定理2 考虑带有变换误差函数(14)和滑模面(15)的离散时间非线性系统(1),滑动变量s(k)可以在控制律(21)的作用下保持在一定区域内,同时变换误差的有界使得指定的追踪性能被保证。 证明 首先通过之前构造的符号关系来讨论θ(k)与ε(k)之间的大小关系,由式(25)可得 再由1<κ<2和引理2可知:当θ(k)>0时,有θ(k)>ε(k)>0;当θ(k)<0时,有θ(k)<ε(k)<0。 步骤1 由式(23)可知 由于s(k)和θ(k)符号相同且ε(k)tan(θ(k))+κ>0,不难得出Δs(k+1)s(k)<0,这也就意味着若滑动变量s(k)在准滑动域外时,会在接下来的时刻向准滑动域收敛。 步骤2 由之前对ξ(k+1)的定义可得 (28) 定义如下的准滑动域: 当s(k)∉Λ时,由步骤1可知滑动变量s(k)会逐渐向准滑动域Λ收敛。当s(k)∈Λ时,由式(23)和上述推导过程可以保证k+1时刻的滑动变量同样被约束在准滑动域内,即s(k+1)∈A。 回顾公式(15)不难看出ε(k)有界,也就意味着追踪误差满足条件(13)。同时通过式(28)和反正切函数的性质可以进一步给出k+1时刻的追踪误差在如下范围内: -ρ(∞)-τs 综上,滑动变量s(k)和追踪误差e(k)的全局有界性得证。 为了验证所设计的具有指定性能的无模型自适应滑模控制方案的有效性,考虑如下的离散时间非线性模型: 参考信号选择为 对控制效果有较大影响的一些参数和初值选择如下:γ=0.03,γ越大,可调边界的收敛速度越快;ρ(∞)=0.05,决定着稳定后误差的约束范围和跟踪效果;τs=0.001,与滑模控制的抖颤影响成正比;κ=1.6,对控制的跟踪精度有一定的影响;ρ(0)=0.5,代表可调边界的初始值;α(0)=β(0)=5,决定了初始状态下可调边界的放大比例;ψ(0)=[1.8;8.2],为伪偏导数时变向量的初始值,影响着整体的控制性能。其他参数选择为:σ=δ=0.1,μ=λ=1。将所提出的方案与传统的无模型自适应方案和文献[19]中的无模型自适应滑模控制方案相比较,在关键参数一致的情况下,各控制方案的跟踪效果如图1所示,所提出方案的跟踪误差约束效果如图2所示。 图1 跟踪效果对比曲线Fig.1 Tracking effect comparison curve 从图1的控制效果可以看出,3种控制方案均可以起到较好的跟踪效果,并基本消除了滑模控制所带来的抖颤影响,而所提出的方案也具有更为优秀的快速性和跟踪精度。 图2 跟踪误差约束效果Fig.2 Tracking error constraint effect 从图2的跟踪误差约束效果可以看出,提出的方案在所有时刻都可以将追踪误差限制在一定范围内。由此也验证了所提出的具有指定性能的无模型自适应滑模控制方案的有效性。 本文对于一类离散时间单输入单输出系统提出了一种新颖的带有指定性能的数据驱动自适应滑模控制方案。在无模型自适应控制的框架下,将一种带有正切型误差变换函数的指定性能控制方法与滑模控制方法相结合,保证了追踪误差在任意时刻都可以收敛到指定的范围中。通过构造参数符号之间的关系证明了滑动函数的有界性,并仿真验证了所提出方案的可行性与优越性。未来的研究工作将会考虑多输入多输出系统和多智能体系统,并对现有方案进行进一步的优化与加强。
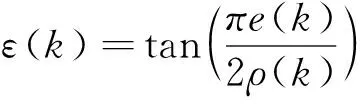
1.3 修改收敛域
2 具有指定性能的无模型自适应滑模控制
2.1 控制器设计
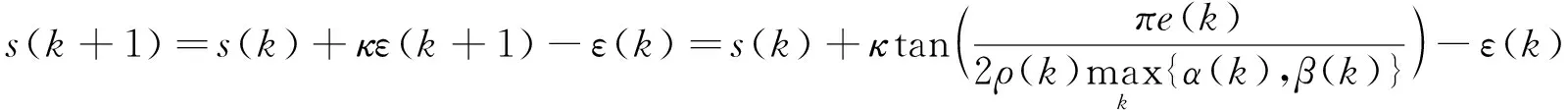
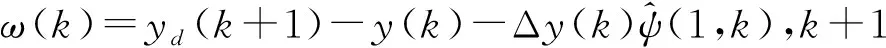
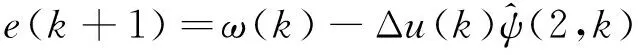



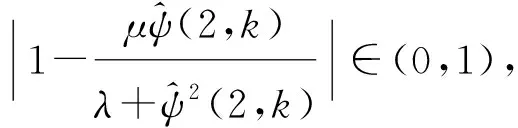

2.2 符号关系的构造
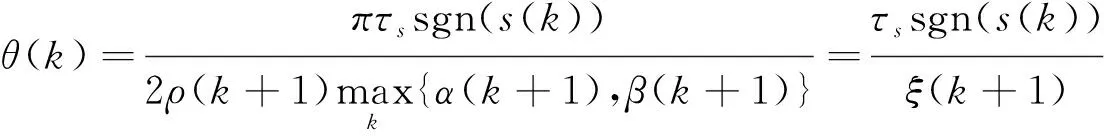

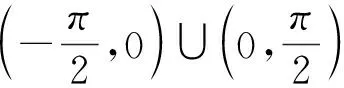
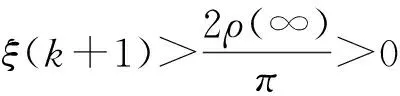
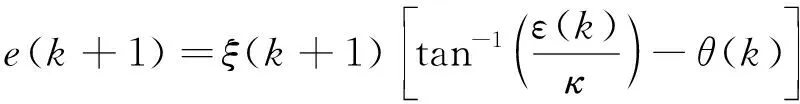
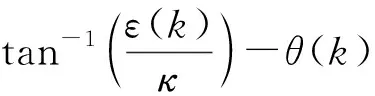



3 控制系统的稳定性分析


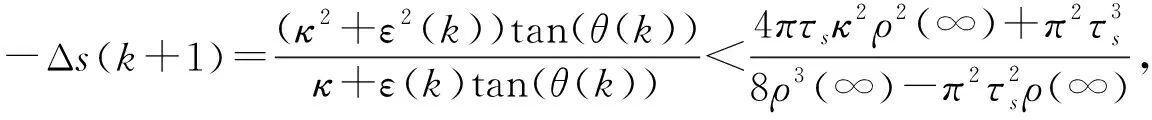
4 仿真验证

5 结 语

