埋地管道关阀水锤数值模拟及结构响应流固耦合分析

虞学军 郑舟斌 熊伟东 金建波 张文奇

（1.舟山市特种设备检测研究院；2.杭州市特种设备检测研究院；3.浙江大学能源工程学院）

管道广泛应用于城市供水/暖、化工及核电等行业中，对于长距离管道,为了布设需求，常常以埋地的方式进行布管。 但有时管道部件运行状态的突然改变（如下游阀门的突然关闭）会引起管道内流体流动状态的瞬间变化， 产生流体冲击力，并在介质弹性作用下持续较长时间。 这种管道流体动态过渡的过程， 会导致系统部件振动，严重时会引起管道的破坏和断裂，这种现象称为水锤［1～4］。 水锤引起的埋地管道损坏，使埋地管道的检测频率和成本大幅提高。 因此，研究水锤造成的冲击对管道的可靠性分析和事故预测至关重要。

水锤导致埋地管道振动甚至损坏，是一种典型的流体流动现象引起的结构振动。 需要在研究水锤的水动力学特性的基础上，再进行管道结构力学的研究。

对于水锤的水动力学特性的试验研究，Ruus E和Karney B B在考虑管道常数和摩擦参数的基础上， 探讨止回阀关闭后引起的水锤波特性，确定了水锤影响下泵不同位置压头的升高和降低的规律［5］。在理论研究的方法方面，早期主要基于特征线法进行。 如Tian W X等通过特征线法研究并联泵交替启动过程中的阀门水锤现象，并提出采用阻尼矩阵降低止回阀的关闭速度的方法，以减轻阀门水锤的潜在危害［6］。 由于特征线法主要针对管道系统研究，结果只可得到关键节点的动态数据，无法从内流场角度进行分析，也就无法进一步将内流场的压力等数据作为载荷进一步研究结构力学的流固耦合。Al-Khomairi A M通过实验证明基于特征线法计算瞬态管道流动存在误差［7］。

基于管道水锤的水动力学特性的研究，Keramat A等率先进行管道水锤的流固耦合特性研究，但采用的方法是特征线法-有限元法，只能计算管道的一维变形［8］。 随着计算流体动力学（CFD）的发展和计算机技术的进步。 CFD方法相比传统的一维方法，其结果具有更高的准确性且更加详细。 Wu D Z等采用Fluent软件对管道系统的阀门快速开启过程进行模拟， 模拟结果与PIV实验结果有良好的吻合度，得到过渡过程中内流畅的瞬态演化过程［9］。 将CFD应用在水锤的研究中，尤其是将CFD得到的压力等流场数据作为载荷，并通过计算结构动力学（CSD）方法研究管道结构在水锤影响下的响应特性，可以得到传统一维方法难以计算的管道水锤流固耦合特性。

综上所述， 探索一种将CFD和CSD耦合的计算方法，以准确预测埋地管道的关阀水锤水动力学特性，并得到管道结构的响应特性，在得到管道水锤的流固耦合机理的同时，还能对水锤引起管道破坏的位置进行预测，减少埋地管道检测的成本。 因此，以Bergant经典管道关阀水锤试验［2，3］为基础，通过多种CFD方法探究最优数值解法，再采用流固耦合的方法， 借由CSD软件分析埋地管道在水锤压力波载荷下的响应特性，揭示管道结构的振动机理。

1 数值计算模型

通过流固耦合方法分析管道关阀水锤的水动力学特性和结构响应特性， 需要分别建立CFD计算模型和CSD计算模型。

1.1 CFD计算模型

澳大利亚研究委员会（ARC）曾经针对管道的水锤进行了试验研究。 该水锤试验主要由Bergant A完成。 试验台由一根长37.2 m，内径22 mm，壁厚1.6 mm的管道作为试验段（图1），两端连接有球阀和水箱，球阀的下游设有段管道和水箱，两水箱间连有压力调节器，并由计算机控制水箱的压力。 此外，试验台还包括安装在管道试验段的压力传感器和数据采集仪。 Bergant A完成了多组试验，通过关阀使管道试验段中产生水锤波，并测量水锤波的特性。 其中，管道入口压力为0.32 MPa， 流场初始速度为0.1 m/s被武汉理工大学的杨成选取，并通过ANSYS CFX计算软件进行数值模拟，并分析了多种初始流速和关阀速度对水锤特性的影响，但其计算值与试验值吻合性较差［10］，而且没有得到压力波的衰减规律。 为此，笔者采用相同的工况，在上述研究的基础上继续进行数值方法的研究，以探索水锤数值模拟的最优方法。

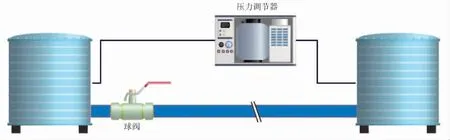
图1 水锤试验台示意图

1.1.1 网格的收敛性分析

为了实现对发射系统的CFD模拟， 需要对管道试验段的求解区域进行网格剖分。 相比于非结构化网格， 结构化网格划分方法可在减少网格数的同时，大幅提高网格的质量，尤其可以有针对性地控制特定区域的节点分布， 提高计算的收敛性和光滑性。此外，为了避免网格划分对计算结果产生影响， 采用Roache提出的网格收敛系数法（GCI方法） 对网格收敛性进行检验。 GCI方法的指标——GCI值是模拟值偏离渐进数值的度量。选择两种网格划分方案，即粗糙网格（网格数为96 065）和加密网格（网格数为704 267），如图2所示，加密网格方案中网格的3个方向的尺寸，均为粗糙网格划分方案的一半。 经计算，加密网格方案的GCI值小于1%，满足网格收敛性要求。 因此，采用加密网格方案进行数值模拟。

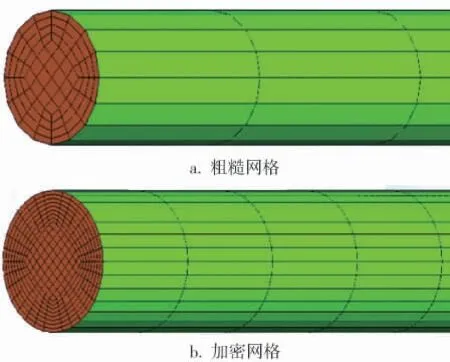
图2 网格划分方案示意图

1.1.2 求解方法和设置

为了模拟关阀引起的水锤波，需要选择合适的模拟阀门关闭过程的方法——控制边界法和模拟关阀法。

控制边界法，即设定连接阀门的管道出口为速度出口边界条件，并且在一定时间内衰减为0 m/s，这也是文献［10］选择的方法。 在选择的工况中，速度出口的边界条件初始为0.1 m/s，并且在0.009 s内线性衰减为0 m/s；管道入口处的边界条件为压力入口，恒压0.32 MPa。

模拟关阀法， 即额外建立球阀的流体域，通过旋转球阀的流体域实现关阀过程的模拟，该方法的流体域设置如图3所示， 球阀的两个交界面分别与管道的上下游贴合，此时为球阀的关闭状态，管道为不流通状态。 在选择的工况中，球阀初始为全开，并且在0.009 s内匀速关闭；管道入口处的边界条件同前一种。

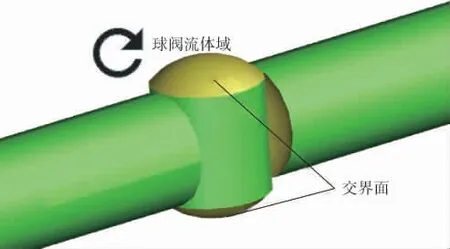
图3 模拟关阀数值方法的流体域

由于文献［10］ 基于CFX求解器进行数值模拟， 为了探寻模拟水锤事件的最优方法， 采用Fluent求解器进行上述两种方法的求解。 求解的过程中，湍流模型选用对强逆压梯度的流动具有很好的计算精度的SST k-ω；离散方程的求解采用压力速度耦合的Coupled算法。阀门网格的转动采用动网格方法实现， 通过通过用户自定义函数（UDF）控制阀门匀速关闭，实现阀门由全开度至闭合状态。 在计算中，考虑流体的可压缩性，通过UDF控制密度随压力变化来反映水的可压缩性变化规律，其表达式为：

式中 K——水的体积弹性模量，2.18GPa；

p——水的实时压力，Pa；

pop——标准状况下大气压力，101 325 Pa；

ρ——水的密度，kg/m3；

ρref——标准状态下水的密度，998.2 kg/m3。

单个时间步长为0.000 5 s， 单个时间步迭代20次；总的计算时长为0.5 s，共1 000个时间步。

1.2 CSD计算模型

对在水锤波作用下的管道结构响应特性的分析，采用与试验相同的管道，但是为了贴合实际工况，材料选用不锈钢以替代铜。 同样，对管道进行结构化网格划分，网格如图4所示。

图4 CSD计算模型网格

计算模型的载荷包括重力载荷和随时间变化的内部流体压力载荷。 为了加载时刻变化着的压力载荷，先选用ANSYS的Transient Structural模块进行结构动力学计算，该模块可以充分考虑载荷变化。再通过ANSYS的ACT扩充功能，提取CFD计算得到的管道壁面的实时载荷，同时提取载荷的大小、时间和网格位置信息，并作为载荷施加给管道结构。

采用弹性约束的方式模拟土壤对管道的作用，弹性约束以管道的外壁面为边界，基础的刚度为使管道结构产生单位法向偏移所需要的压力。 不同地基土的抗压刚度系数各不相同，相差数倍或十几倍，因此以典型的碎石土（硬质土壤）为管道埋地环境，其抗压刚度为70 kN/m3，并作为约束。

2 数值模拟与试验结果对比

水锤波引起的压力变化是水锤最重要的特性，因此选用水锤事件中的压力变化，作为衡量数值模拟与真实情况贴合程度的指标。 分别总结Bergant A试验、文献［10］和上述基于Fluent求解结果中的阀门上游点和管道轴向中点的压力随时间变化的规律，其中，阀门点处压力变化规律如图5所示。

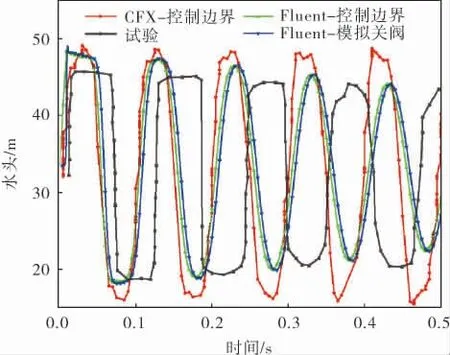
图5 阀门点处压力变化规律

从水锤波的周期入手，试验测得的水锤波周期约为0.135 s，CFX-控制边界法为0.095 s，Fluent的两种解法同为0.105 s。 按照水锤波理论，其压力波周期T和波速a的关系式为：

式中 L——管长，m。

由式（2）计算得到的水锤波速分别为：试验值1 102 m/s；CFX-控制边界法1 566 m/s；Fluent控制边界和模拟关阀法1 417 m/s。 可见，Fluent模拟水锤波的波速和周期更接近试验值，模拟值和试验值的偏差缘由为：水锤波会在试验中管道上游的水箱中继续传递， 而模拟中忽略了水箱，受水箱影响的试验数据会使计算得到的波速略低；水锤发生时会伴随着一定的空化现象，水锤波在水蒸气中的传播速度远低于液态水，而模拟忽略了空化现象，算得的波速会偏高。

在水锤波压力幅值方面， 基于Fluent的两种方法计算结果几乎相同， 且在第1周期中呈短时间内在最高值维持不变的规律，这与试验结果相同，而且是CFX求解器没能成功仿真的现象。对于压力波波峰，试验值为0.45 MPa（水头46.01 m）；CFX求解的结果为0.49 MPa（水头50.10 m），与试验值偏差为8.89%， 且出现在计算的最后一个周期，在0.9 s时刻［10］；Fluent求解的结果为0.48 MPa（水头49.07 m），出现在水锤波的第1个周期，与试验值的偏差为6.67%。 可见，Fluent的求解结果更精确。此外，CFX求解器没能得到水锤波压力波峰随周期递减的规律， 而Fluent求解结果中水锤波波峰递减规律与试验结果相同。

管道中点压力的变化规律如图6所示。 同样的， 基于Fluent的模拟关阀法和控制边界法得到的结果相同， 且在幅值和周期上相较CFX求解器更为准确。 此外，基于Fluent求解水锤的优势在于可以很好地模拟水锤波压力衰减规律。

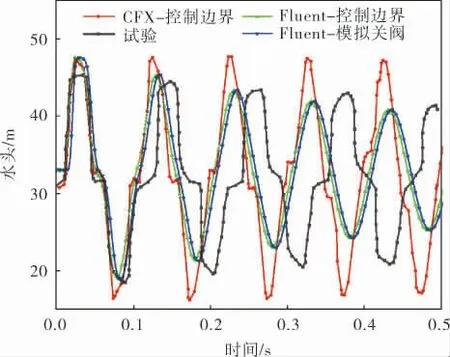
图6 管道中点压力变化规律

3 管道关阀水锤过程中压力、 流速变化和内流场分析

由上述分析可知， 通过Fluent求解器得到的水锤波压力变化规律更趋近于试验值， 因此，采用Fluent模拟关阀法的求解结果分析管道关阀水锤过程中压力、流速的变化和内流场变化。 除阀门处和管道中点外，同时监测了管道入口和距管道入口5 m处的两个测点。 各测点压力变化规律如图7所示。 由图7可以看出，水锤波的压力峰值随距阀门的距离逐渐降低。 入口处压力由边界条件确定，始终保持在恒定初压，因此与试验的真实情况存在偏差，这也是引起数值方法产生误差的重要因素。

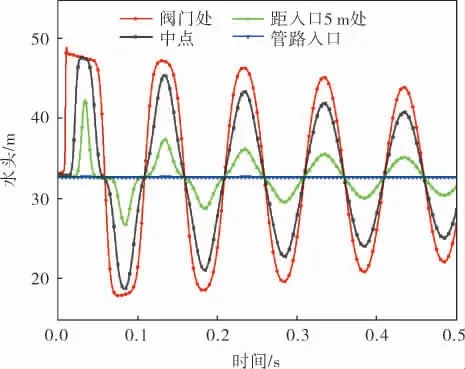
图7 管道各测点压力变化规律

各测点速度变化规律如图8所示。 对于阀门处，由于阀门关闭，阀门处流体流速迅速降低至0 m/s，期间有轻微波动。在管道的其他位置，流体的流速随压力波在±0.1 m/s的幅值范围内波动。但在第1个周期内， 各测点的速度变化规律并不同步，而是存在一定的相位差，这意味着在管道的特定位置，流体流速梯度较大，流体相互挤压，甚至产生相向流动。

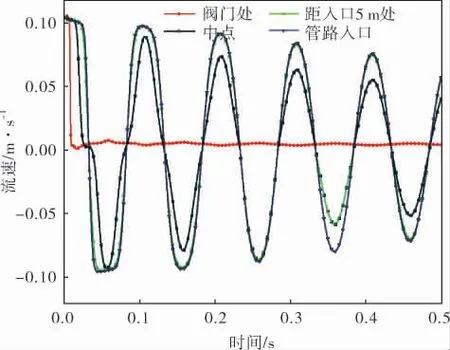
图8 管道各测点速度变化规律

图9为0.127 s时阀门上游区域流场的速度云图和矢量图。 由图9可看出，因阀门关闭，上游区域的流速降低至0 m/s，且流体随水锤压力波反向流动，但更上游的流体由于惯性，保持原先的正向流动，故在该区域产生了相向流动的现象。

图9 管道内流体相向流动的区域

4 水锤压力载荷下管道结构力学特性

图10是管道结构在水锤载荷作用下，振动加速度和应力随时间的变化规律。 对于管壁的变形加速度，压力波的波峰和波谷均会引起管壁的振动，且幅值达到了一个重力加速度。 在同一个水锤波周期内， 变形加速度会出现两次波峰和波谷。 所以，在水锤的影响下，管道会剧烈振动，与土壤的冲击也会使得结构损坏。 对于管道结构的应力，可以发现管道内的初压引起了管壁一定的压力，当水锤波压力波峰出现时由于作用在壁面的压力陡然增大， 应力的最大值也随即增大，当压力值达到最大时，应力值也达到最大，升高幅度达到了46.4%，这种应力的急剧增大，极易引起结构的破坏。 而水锤压力波波谷到达时，由于管道内部分位置的压力降低，使得应力的最小值降低。 但由于压力波在管道内时刻传递，这使得不同位置的应力不同， 既存在最小值也存在最大值。

管壁应力以上述规律呈现明显的周期性，且随着周期增大应力的变化减小。 图11为4个不同时刻应力最大值和最小值出现的位置，4个时刻分别为图10所示的t1～t4。 由图11可以看出，水锤压力波波峰时，应力最大出现在阀门处，且最小值在入口处管段；当压力波波谷时，应力最大值在管道入口，而最小值在管道中段。 而且，下一个周期也呈现出相同的规律。

图11 管道应力最大值和最小值位置

5 结论

5.1 相对于CFX，Fluent求解水锤压力波的幅值和变化规律更为准确，且控制边界法和模拟关阀法得到的结果相同。 为了得到更为准确的周期信息，需要建立包括水箱在内的全流体域。

5.2 在水锤波的影响下，管道内流体流动方向发生改变，但不同位置的流速改变不同步，在特定位置会出现流体相向流动，产生挤压。

5.3 水锤压力波会引起管道剧烈振动，且一个压力波周期内，会导致两个振动周期。

5.4 水锤压力波波峰会引起管道结构的应力最大值显著增大， 增幅达46.4%， 极易引起结构破坏。