PMSM基于模型辅助的LADRC控制研究

姜 泽,严伟灿,魏学良,黄晓艳

(1.浙江大学 电气工程学院,杭州 310027;2.卧龙电气驱动集团股份有限公司,浙江 绍兴 312300)

0 引 言

永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)因其具有效率高、功率密度高、可靠性高等优点，在新能源汽车、电动航空、运动伺服、数控机床、工业及民用等领域得到广泛的应用与研究[1-2]。通常地，永磁同步电机速度双闭环控制回路由电流内环和速度外环组成，内、外环通常采用PI控制。传统PI控制器参数适应性差，当控制对象工况复杂或参数发生变化时，需重新调整控制器参数来保证系统的稳定性和良好的控制品质[3]，而PMSM内部是一个多变量、时变和复杂非线性电磁系统，当系统面对负载突变或不确定干扰时，传统PI控制难以达到较好的抗干扰能力，容易产生系统超调和振荡等问题。因此，对PMSM控制系统而言，提升其控制系统的抗干扰性能尤为重要。

针对PI控制存在的缺陷，韩京清先生于1998年在文献[4]中提出了自抗扰控制(Active Disturbance Rejection Control,ADRC)。该控制算法能对系统的内、外干扰进行实时观测和补偿，具有较强的抗干扰能力和良好的控制性能，因此被广泛应用于诸多领域。随着ADRC的发展，高志强教授针对ADRC控制器参数多且难以整定等问题，在文献[5]中提出了控制器参数基于带宽整定的线性自抗扰控制(Linear Active Disturbance Rejection Control,LADRC)，LADRC在继承了传统ADRC优点的基础上，极大的简化了控制器参数的整定，推动了LADRC工程应用研究。文献[6]中针对传统LADRC的线性扩张状态观测器抗扰和抗噪双优化的问题，提出了一种自适应调整的变增益线性扩张状态观测器的控制策略，有效提高了PMSM调速系统的抗干扰和抗噪性能。文献[7]中针对永磁直线电机对扰动敏感的问题，提出一种位置环线性自抗扰控制与电流环PI控制相结合的控制策略，实现了永磁直线电机的高精度控制。文献[8]中设计了一种PD控制器与线性扩张状态观测器改进型的线性自抗扰控制策略，避免了速度估计信号的滞后影响，实验验证了该控制策略的有效性。文献[9]针对多电机启动时系统存在同步误差大、跟踪性能和鲁棒性差的问题，提出了一种改进的二阶LADRC与改进型速度补偿器相结合的新型偏差耦合控制结构，有效的提高了多电机同步控制系统的控制性能。文献[10]针对电机电感参数失配时传统电流解耦控制存在解耦效果不佳的问题，提出了一种基于增益连续扩张状态观测器的电流解耦控制策略，实验结果有效的验证了该方法的有效性。

基于以上分析，针对LADRC控制器在带宽不变的情况下，当PMSM负载突变时，线性扩张状态观测器(Linear Extended State Observer,LESO)存在观测精度低、观测负担大的问题，提出了一种基于PMSM已知干扰的双闭环一阶A-LADRC(Assist-Linear Active Disturbance Rejection Control,A-LADRC)控制策略。该控控制策略将速度环与电流环控制回路中的PMSM已知扰动分别补偿到外环与内环一阶LADRC控制器中，得到了PMSM双闭环一阶A-LADRC速度控制系统。在Matlab/Simulink中分别搭建了传统PI控制、传统LADRC控制和A-LADRC控制仿真模型。仿真结果表明：PMSM速度控制系统在负载突变时，本文提出的一阶A-LADRC控制系统相比传统的一阶LADRC和PI控制系统具有速度抗干扰能力强，二次稳态响应时间短及系统鲁棒性强等优点。

1 永磁同步电机数学模型

永磁同步电机是一个复杂的非线性时变系统，为简化分析，忽略定子铁芯饱和、涡流和磁滞损耗，定子与转子产生正弦分布的磁场，定子绕组三相对称。根据基尔霍夫电压定律，可得永磁同步电机两相旋转坐标系下d-q轴电压方程为

(1)

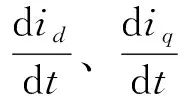
整理式(1)可得到d轴和q轴的电流方程：

(2)

永磁同步电机电磁转矩方程为

(3)

式中，Te为电磁转矩；p为电机磁极对数。

永磁同步电机机械运动方程为

(4)

式中，TL为电机负载转矩；J为转动惯量；B为转子阻尼系数；ωm为转子机械角速度，ωe=pωm；dωm/dt为转子机械角加速度。

对表贴式PMSM而言，d轴和q轴电感相等，即Ld=Lq且B=0。令id、iq、ωm为PMSM的状态变量，将ud、uq、TL作为电机的输入量，由式(2)、式(3)、式(4)可得PMSM的状态方程如下：

(5)

根据文献[11]，对式(5)进行拉氏变换得到PMSM传递函数控制框图，如图1所示。

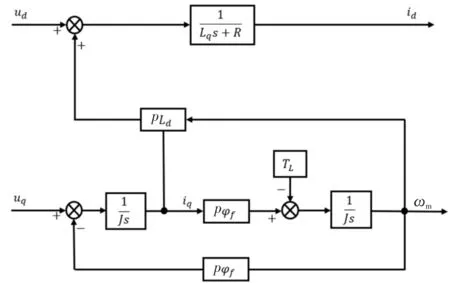
图1 PMSM传递函数控制框图

图中，ud、uq、TL分别为整个控制系统的输入量，ωm系统输出量。当系统负载TL变化时，速度ωm的变化使得反电动势pφfωm发生改变，进而改变q轴电流，最终实现系统的调压调速控制。

2 一阶LADRC控制器

2.1 基本结构

原始ADRC线性化后去除了跟踪微分器配置的过渡环节，为保证整个控制系统无超调，本文采用的一阶LADRC控制器结构如图2所示。

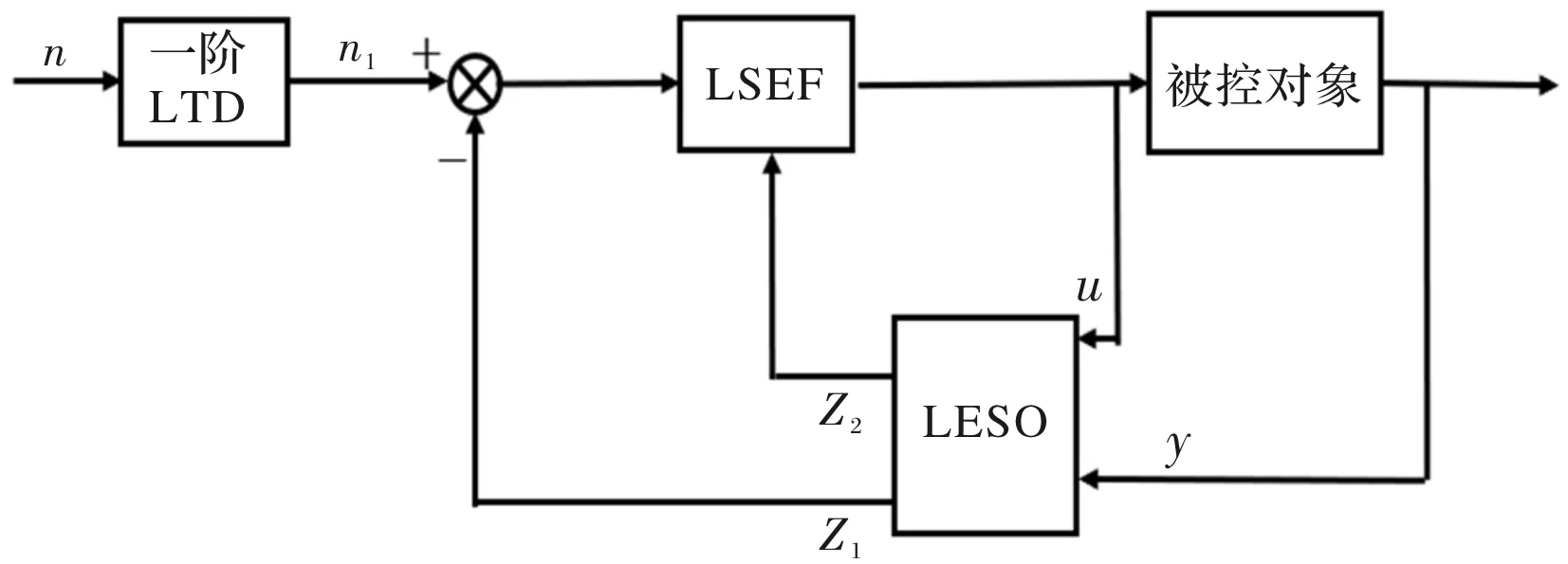
图2 一阶线性自抗扰控制器结构

图中，一阶LTD为一阶线性跟踪微分器，其本质是一个惯性环节，主要作用是跟踪目标信号并消除因系统初始控制力较大而造成的超调；LSEF为线性状态误差反馈控制律，其本质是一个比例环节和扰动补偿的组合控制，其作用是对LESO估计的扰动信号进行线性组合产生控制量；LESO为线性扩张状态观测器，其作用是观测估计系统固有状态变量和扩张的状态变量，为LSEF提供反馈信号。

2.2 控制算法

对速度控制系统，设系统输入的期望速度为n，被控对象输出的实际速度为y，则一阶LADRC控制算法表示如下：

(6)

3 一阶A-LADRC控制设计

3.1 速度环A-LADRC控制器设计

永磁同步电机是一个非线性时变系统，因此其速度环控制回路的干扰主要由电机参数的不准确性、负载的不确定性以及电流内环控制误差等因素而产生。由式(4)可知，影响速度的因素有电机参数、转动惯量及负载。已知速度与角速度关系如下：

(7)

式中，角速度单位rad/s，速度单位r/min。本文采用id=0的双闭环矢量控制策略，将式(6)和式(3)带入式(4)中可得：

(8)

设b0s=45pφf/Jπ，a1=-B/J，f1=-30TL/Jπ，则式(7)可表示为

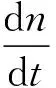
(9)

将式(8)中PMSM速度控制的已知干扰a1融入LESO中，进而得到如图3所示的速度环一阶A-LADRC控制器结构。

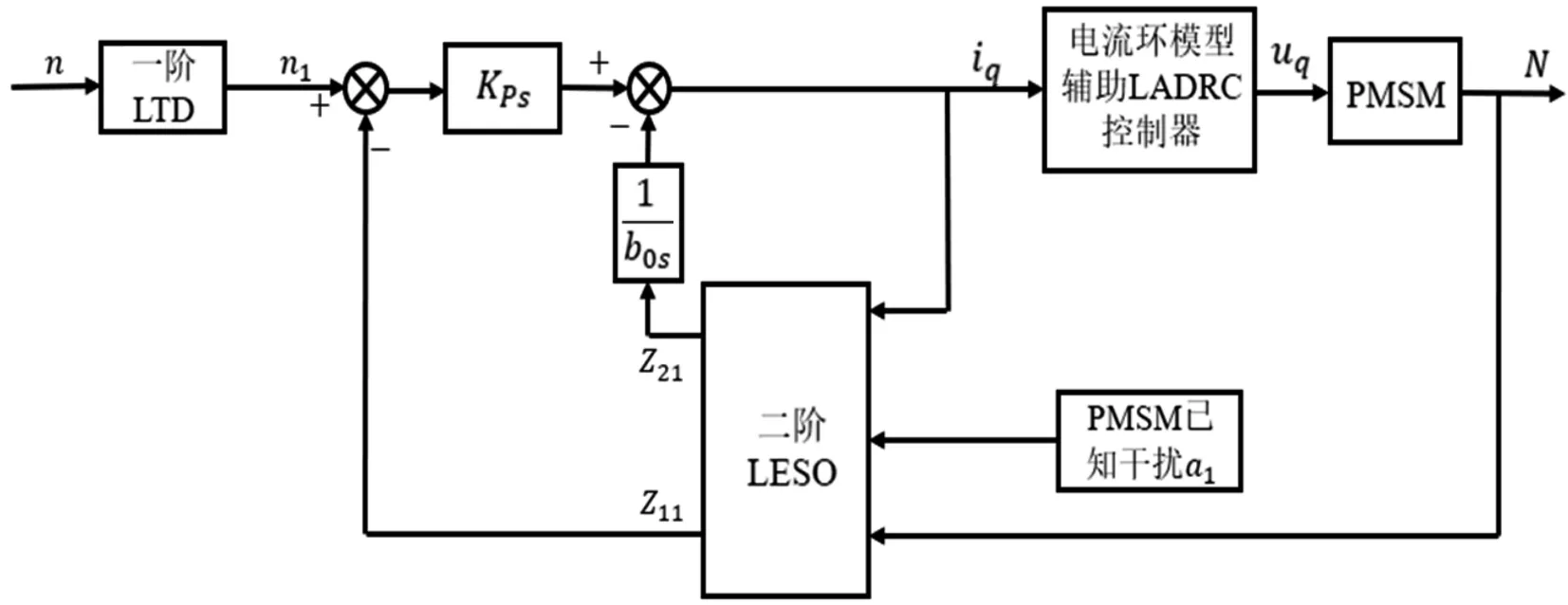
图3 速度环一阶A-LADRC控制器结构

图中，KPs为速度环比例系数；b0s为速度环一阶LADRC控制器扰动补偿系数；Z21为速度环总扰动观测估计值；Z11为速度环速度观测估计值；N为永磁同步电机实际速度。

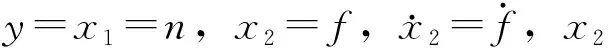
(10)

(11)

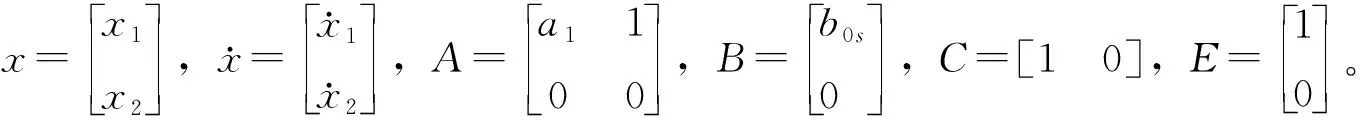
(12)

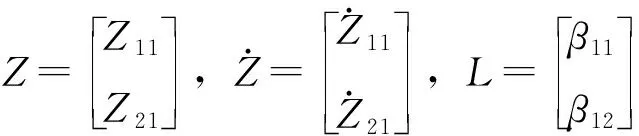
|sE-(A-LC)|=(s+ω0s)2

(13)

由式(12)，解得带有已知干扰LESO增益系数如下：

(14)

根据以上分析，得到设计的模型辅助LESO如下：

(15)

式中，e1为速度误差；ω0s为速度环LESO带宽。

综上所述，可得到设计的速度环一阶A-LADRC控制器算法如下：

(16)

在Matlab/Simulink中搭建速度环一阶A-LADRC控制器仿真模型如图4所示。

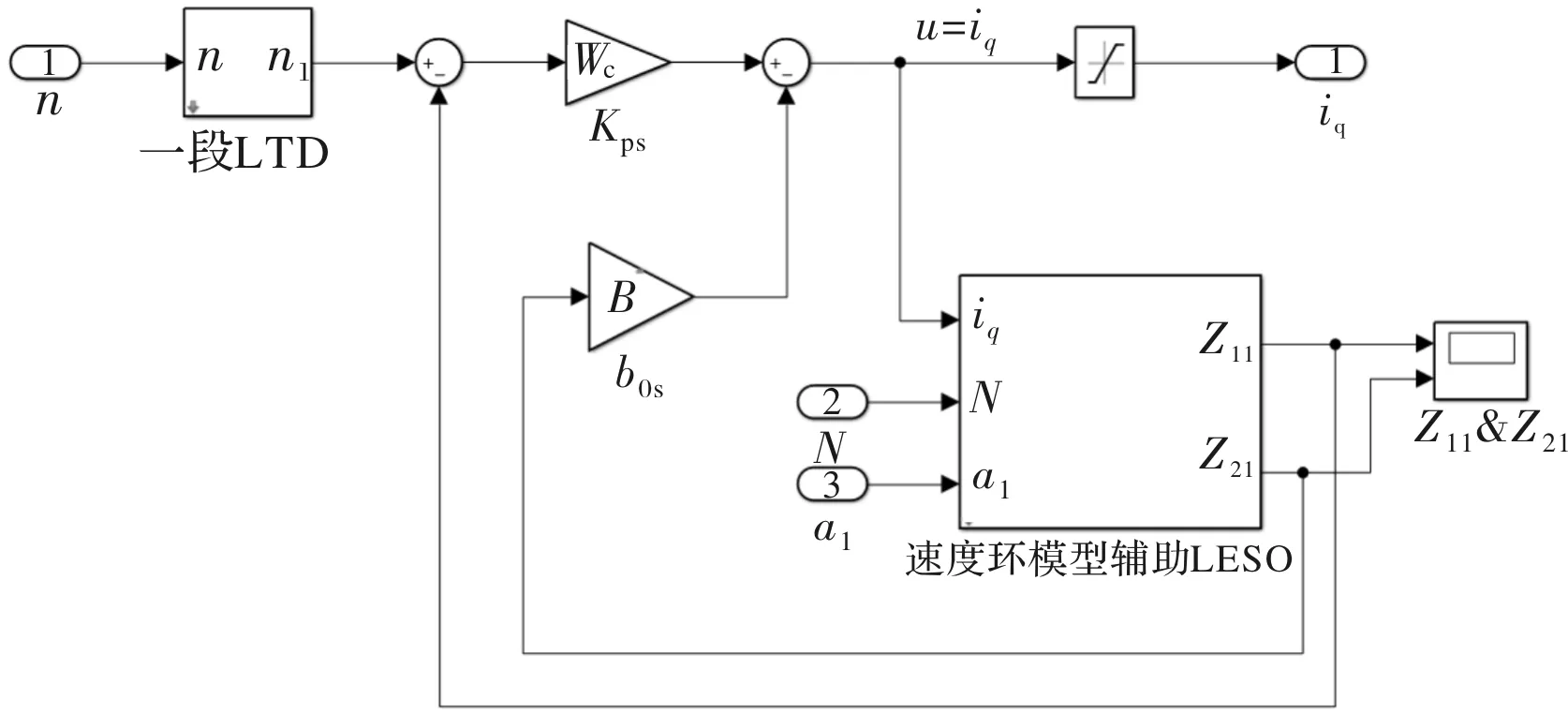
图4 速度环一阶A-LADRC控制器仿真模型

3.2 电流环A-LADRC控制器设计

采用id=0的矢量控制，控制q轴电流即可实现电机速度控制，故只需设计q轴A-LADRC控制器。根据式(2)可得：

(17)

设b0c=1/Lq，a2=-R/Lq，f3=-(pωmφf)/Lq，则式(16)可表示如下：

(18)

分析式(17)，f3为已知电机内部时变干扰，a2为已知干扰，a2对电流环iq的控制直接产生影响，将a2作为电流环已知干扰融入LESO设计中，进而得到如图5所示的电流环一阶A-LADRC控制器结构。

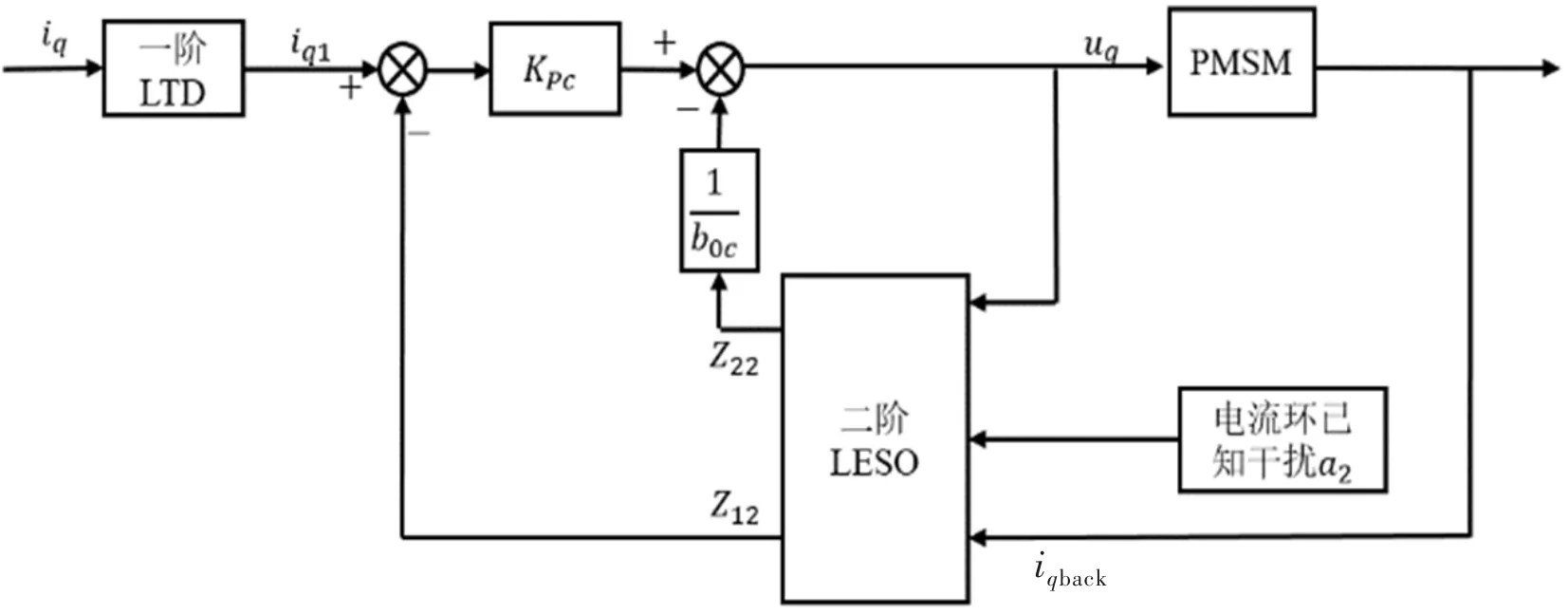
图5 电流环一阶A-LADRC控制器结构

图中，iq1为速度环输出量iq的跟踪信号；KPc为电流环比例系数；b0c为电流环一阶LADRC控制器扰动补偿系数；Z22为电流环总扰动观测估计值；Z12为电流环q轴电流观测估计值；ipback为q轴实际电流反馈信号。

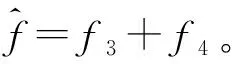
(19)

同理，电流环一阶A-LADRC控制器设计与速度环一阶A-LADRC控制器相同，整理得其控制器算法如下：

(20)

式中，ω0c为电流环LESO带宽；e2为电流误差。

在Matlab/Simulink中搭建电流环一阶A-LADRC控制器仿真模型如图6所示。

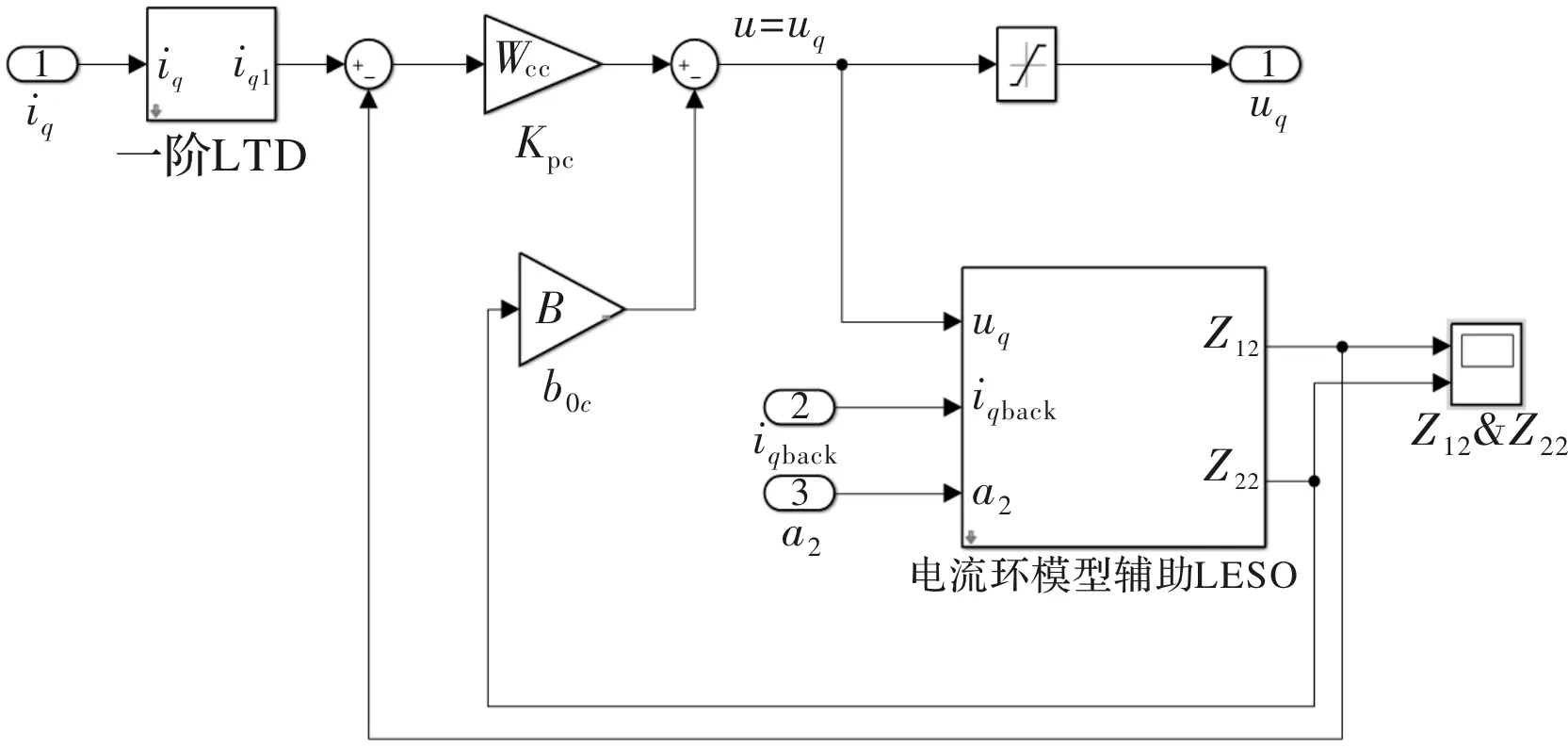
图6 电流环一阶A-LADRC控制器仿真模型

由文献[5]可得LADRC控制器比例参数如下：

(21)

式中，ωcs为速度环控制系统带宽；ωcc为电流环控制系统带宽。通常，观测器带宽ω0与控制系统带宽ωc存在如下关系：

ω0=(3～10)ωc

(22)

搭建仿真系统速度环LESO带宽ω0s=4ωcs，电流环LESO带宽ω0c=3ωcc。

4 仿真结果分析

为有效验证设计的双闭环一阶A-LADRC控制策略相比于传统一阶LADRC和PI控制策略具有更好的控制性能，在Matlab/Simulink中分别搭建双闭环一阶LADRC控制仿真模型、双闭环PI控制仿真模型和设计的一阶A-LADRC控制仿真模型。图7为基于PMSM模型辅助的一阶A-LADRC双闭环控制仿真模型。

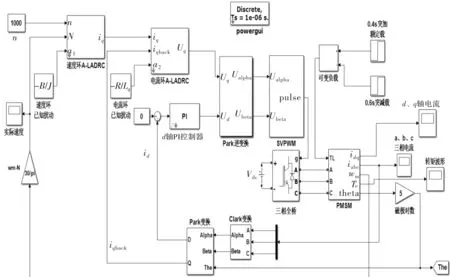
图7 基于PMSM模型辅助的一阶A-LADRC仿真模型

图中，ωm-n为转子机械角速度与速度的转换模块；powergui为系统仿真采样时间模块；PMSM为电机本体仿真模型。永磁同步电机参数如表1所示。

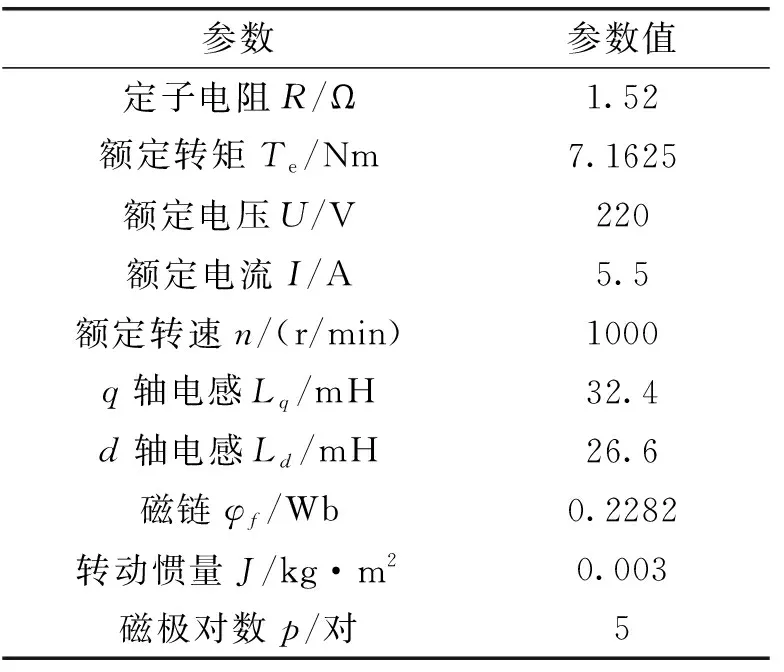
表1 永磁同步电机参数

传统PI控制、传统LADRC控制和设计的A-LADRC控制仿真系统模型的控制器参数如表2所示。

表2 仿真系统各控制器参数

期望速度为1000r/min，空载起动，仿真时间为1 s，0.4 s突加额定负载7.1625 Nm，0.6 s负载突减至4 Nm。在LESO带宽参数相同的前提下，得到传统LADRC控制、传统PI控制与本文设计的A-LADRC控制速度对比响应曲线如图8所示。

分析图8可知，传统PI控制存在启动超调，且存在振荡。当负载发生突变时基于模型辅助的A-LADRC控制策略相比传统LADRC控制和PI控制具有超调量小、抗干扰能力强的优势。将图8中速度曲线的负载突变部分进行局部放大，得到如图9所示的负载突变时速度放大对比曲线。

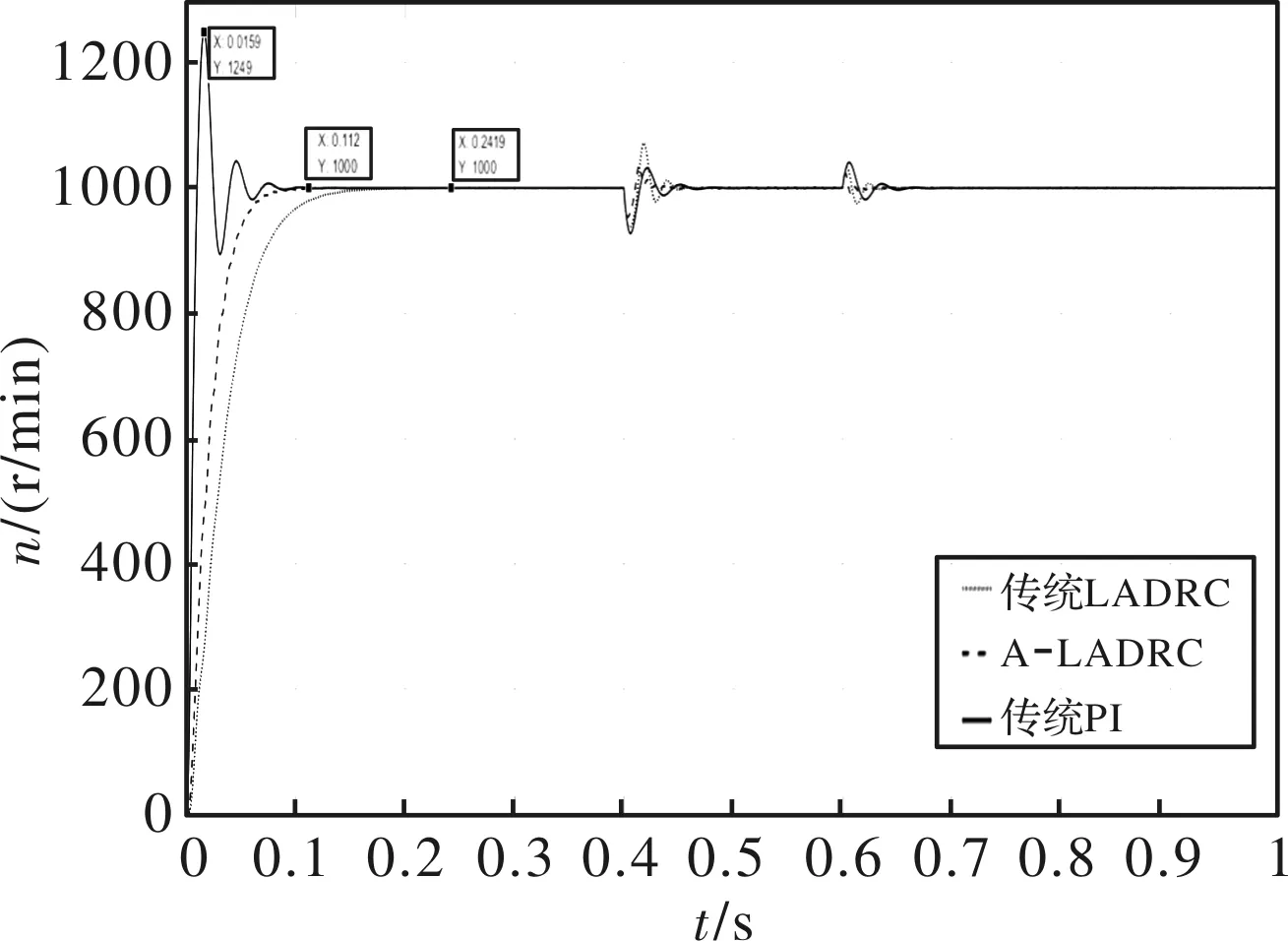
图8 传统LADRC、PI与A-LADRC速度响应曲线

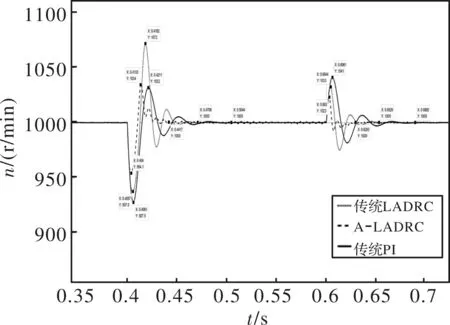
图9 负载突变时速度放大对比曲线

根据图8和图9，可计算得到传统LADRC、传统PI与A-LADRC控制的速度响应曲线的动态性能指标对比表，如表3所示。

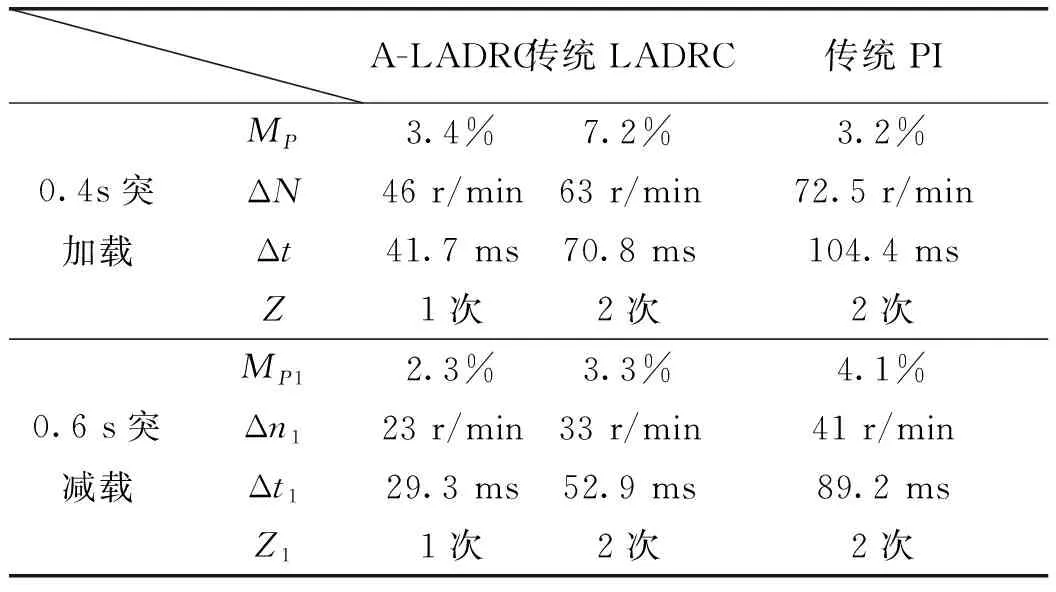
表3 速度曲线动态性能指标对比表

表3中，MP、MP1分别为加载和减载时的超调量；Δn、Δn1分别为加载和减载时的速度变化量；Δt、Δt1分别为加载和减载时再次达到稳态的时间变化量；Z、Z1分别为加载和减载时速度曲线振荡次数。由表3可知，在电机负载发生突变时，笔者设计的A-LADRC控制策略相比于传统PI、LADRC控制具有超调量小、二次稳态时间短、振荡小及速度抗干扰能力强的特点。

5 结 语

针对永磁同步电机负载突变和LADRC控制器带宽不变时，线性扩张状态观测器存在观测精度不高、观测负担大的问题，设计了基于PMSM模型辅助的A-LADRC速度控制策略，有效的提高了观测器的估计精度和减轻了观测负担。仿真结果表明：该控制策略与传统的LADRC控制及PI控制相比，具有速度响应快、二次稳态时间短和抗干扰能力更强的优势。